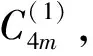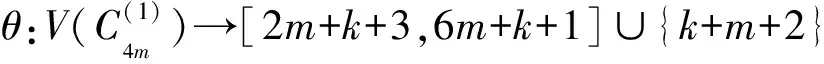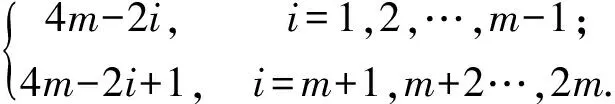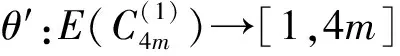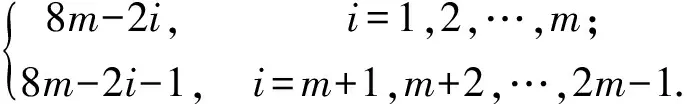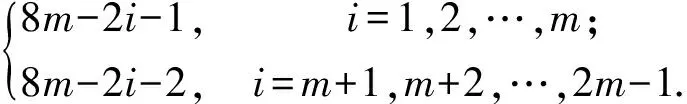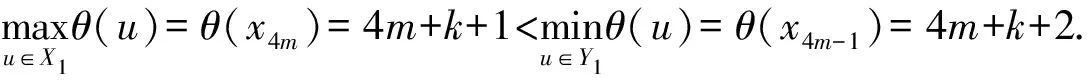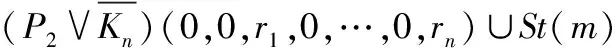非連通圖2C4m∪G的優(yōu)美標號
吳躍生,王廣富,徐保根
(華東交通大學基礎科學學院,江西 南昌330013)
1 引言與概念
本文所討論的圖均為無向簡單圖,V(G)和E(G)分別表示圖G的頂點集和邊集,記號[m,n]表示整數(shù)集合{m,m+1,…,n},其中m和n均為非負整數(shù),且滿足0≤m 圖的優(yōu)美標號問題是組合數(shù)學中一個熱門課題[1-15]. 文獻[1]已經(jīng)證明: 非連通圖2C4m是優(yōu)美圖. 本文討論了非連通圖2C4m∪G的優(yōu)美性. 定義1[1]對于一個圖G=(V,E),如果存在一個單射θ:V(G)→[0,|E(G)|],使得對所有邊e=(u,v)∈E(G),由θ′(e)=|θ(u)-θ(v)|導出的E(G)→[1,|E(G)|]是一個雙射,則稱G是優(yōu)美圖,θ是G的一組優(yōu)美標號,稱θ′為G的邊上的由θ導出的誘導值. 定義2[1]設f為G的一個優(yōu)美標號,如果存在一個正整數(shù)k,使得對任意的uv∈E(G)有 f(u)>k≥f(v)或f(u)≤k 成立,則稱f為G的平衡標號(或稱G有平衡標號f),且稱k為f的特征.圖G稱為平衡二分圖(balanced bipartite graph). 顯然,若f為G的平衡標號,則k是邊導出標號為1的邊的兩個端點中標號較小的頂點的標號. 定義3[1]在平衡二分圖G中,設其優(yōu)美標號θ的特征為k,并且θ(u0)=k,θ(v0)=k+1,則稱u0為G的二分點,v0為G的對偶二分點. 定理對任意正整數(shù)m,設G是特征為k,且缺k+2m+1標號值的交錯圖,則非連通圖2C4m∪G存在特征為4m+k+1,且缺k+1標號值的交錯標號(2m+1≤k+2m+1≤|E(G)|). 定義2C4m∪G的頂點標號θ為 θ(x2i)=2m+i+k+2,i=1,2,…,m-1; θ(x2m)=m+k+2,θ(x2i)=2m+i+k+1,i=m+1,m+2,…,2m; θ(x2i-1)=6m-i+k+2,i=1,2,…,2m; θ(y2i-1)=8m-i+k+1,i=1,2,…,2m-1;θ(y4m-1)=k+10m+1; 下面證明θ是非連通圖2C4m∪G的優(yōu)美標號. (1) θ:X→[0,k]是單射(或雙射);θ:Y→[k+8m+1,q+8m]{k+10m+1}是單射(或雙射); θ:V(2C4m∪G)→[0,q+8m]{k+1}是單射. (2) θ′(x2m-1x2m)=4m, θ′(x2mx2m+1)=4m-1, θ′(x4mx1)=2m, θ′(y4m-1y4m)=8m-1, θ′(y4m-2y4m-1)=8m, θ′(y4my1)=6m-2, θ′:E(G)→[8m+1,q+8m]是雙射; θ′:E(2C4m∪G)→[1,q+8m]是一一對應. 由(1)和(2)可知θ就是非連通圖2C4m∪G的缺k+1標號值的優(yōu)美標號. 令X1=X∪{x2i,i=1,2,…,2m}∪{y2i,i=1,2,…,2m}, Y1=Y∪{x2i-1,i=1,2,…,2m}∪{y2i-1,i=1,2,…,2m}, 所以,θ就是非連通圖C4m∪G的特征為4m+k+1,且缺k+1標號值的交錯標號. 證畢. 引理1 對任意正整數(shù)n,設C4n是有4n個頂點的圈,則C4n存在特征為2n-1,且缺3n的交錯標號. 證明記圈C4n上的頂點依次為v1,v2,…,v4n,定義圈C4n的頂點標號θ為 θ(v2i-1)=i-1,i=1,2,…,2n. 容易驗證,θ就是圈C4n的特征為2n-1,且缺3n的交錯標號. 注意到:3n=(2n-1)+n+1,由定理和引理1得推論1. 推論1 對任意正整數(shù)m,非連通圖2C4m∪C8m存在特征為8m且缺4m標號值的交錯標號. 例1 由推論1給出的非連通圖2C8∪C16的特征為16且缺8標號值的交錯標號為 20,14,19,11,18,15,17,16; 23,9,22,10,21,12,28,13; 0,32,1,31,2,30,3,29,4,27,5,26,6,25,7,24. 引理2[1]如果θ是圖G特征為k的交錯標號,令θ1(v)=|E(G)|-θ(v),v∈V(G),則θ1是圖G特征為|E(G)|-k-1的交錯標號. 由推論1和引理2得推論2. 推論2 對任意正整數(shù)m,非連通圖2C4m∪C8m存在特征為8m-1且缺12m標號值的交錯標號. 注意到:12m=(8m-1)+4m+1,由定理和推論2得推論3. 推論3 對任意正整數(shù)m,非連通圖2C8m∪(2C4m∪C8m)存在特征為16m且缺8m標號值的交錯標號. 例2 由推論3給出的非連通圖2C16∪(2C8∪C16)的特征為32且缺16標號值的交錯標號為: 9,55,10,54,11,52,4,51; 12,50,13,53,14,49,15,48; 64,0,63,1,62,2,61,3,60,5,59,6,58,7,57,8; 40,26,39,27,38,28,37,21,36,29,35,30,34,31,33,32; 47,17,46,18,45,19,44,20,43,22,42,23,41,24,56,25. 由推論3和引理2得推論4. 推論4 對任意正整數(shù)m,非連通圖2C8m∪(2C4m∪C8m)存在特征為16m-1且缺24m標號值的交錯標號. 注意到:24m=(16m-1)+8m+1,由定理和推論4得推論5. 推論5 對任意正整數(shù)m,非連通圖2C16m∪(2C8m∪(2C4m∪C8m))存在特征為32m且缺16m標號值的交錯標號. 由推論5和引理2得推論6. 推論6 對任意正整數(shù)m,非連通圖2C16m∪(2C8m∪(2C4m∪C8m))存在特征為32m-1且缺48m標號值的交錯標號. …… 重復上述過程,可以構造出許多交錯圖. 參考文獻: [1] 馬克杰.優(yōu)美圖[M]. 北京:北京大學出版社,1991. [2] 楊顯文.關于C4m蛇的優(yōu)美性[J].工程數(shù)學學報,1995,12(4):108-112. [3] 吳躍生.關于圈C4h的(r1,r2,…,r4h)-冠的優(yōu)美性[J].華東交通大學學報,2011,28(1):77-80. [4] 吳躍生,李詠秋. 關于圈C4h+3的(r1,r2,…,r4h+3)-冠的優(yōu)美性[J].吉首大學學報:自然科學版,2011,32(6):1-4. [5] 吳躍生.關于圖P6k+53∪Pn3的優(yōu)美性[J].吉首大學學報:自然科學版,2012,33(3):4-7. [7] 吳躍生.圖C7(r1,r2,r3,,r4,r5,0,0)∪St(m)的優(yōu)美性[J]. 吉首大學學報:自然科學版,2012,33(5):1-9. [8] 吳躍生,王廣富,徐保根. 關于C4h+1⊙K1的(Gr1,Gr2,…,Gr4h+1,Gr4h+2)-冠的優(yōu)美性[J].山東大學學報,2013,48(4):25-27. [9] 吳躍生. 關于圈C4h+3的(Gr1,Gr2,…,Gr4h+3)-冠的優(yōu)美性[J].吉首大學學報:自然科學版,2013,34(4): 4-9. [10] 吳躍生,王廣富,徐保根.非連通圖C2n+1∪Gn-1的優(yōu)美性[J].華東交通大學學報,2012,29(6):26-29. [11] Gallian J A A. Dynamic survey of graph labeling[J]. The Electronic Journal of Combinatorics,2013,16(6): 1-308. [12] Golom B S W. How to Number of a Graph:Graph Theory and Computing[M].New York:Academic Press,1972. [13] Gallian A. A guide to the graph labeling zoo[J].Discrete Mathematics,1994,49:213-229. [14] Kathie San Km.Two classes of graceful graphs[J].Ars Combinatioria,2000,55:129-132. [15] Frank Hsu D. Harmonious labelings of windmill graphs and related graphs[J]. Journal of Graph Theory,1982,6(1):85-87.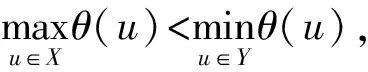
2 主要結果及其證明