半空間上Boussinesq方程組弱解的L2衰減估計(jì)
劉艷梅,高巧琴
半空間上Boussinesq方程組弱解的L2衰減估計(jì)
劉艷梅,高巧琴
(呂梁學(xué)院數(shù)學(xué)系,山西離石033000)
主要研究外力函數(shù)f滿足一定條件時(shí),半空間上Boussinesq方程組當(dāng)n≥3時(shí)弱解的L2衰減.先假設(shè)解光滑,給出了光滑解的一致L2衰減估計(jì),再通過(guò)構(gòu)造逼近解,對(duì)逼近解序列作一致衰減估計(jì),取極限得到弱解的一致L2衰減估計(jì).
Boussinesq方程組;弱解;L2衰減
1 引言
Boussinesq方程組是流體方程中一類重要的方程,它是流體速度場(chǎng)與溫度場(chǎng)耦合而成的方程.本文主要討論當(dāng)n≥3時(shí),Boussinesq方程組在×(0,∞)上弱解的衰減率問(wèn)題:

其中n表示空間維數(shù),u(x,t)=(u1(x,t),u2(x,t),···,un(x,t))表示流體速度向量,θ(x,t)表示溫度,p(x,t)表示壓力函數(shù),f(x,t)=(f1(x,t),f2(x,t),···,fn(x,t))表示外力,u0,θ0表示初始流體速度和溫度,γ≥0和ε≥0分別是流體粘性系數(shù)和導(dǎo)數(shù)系數(shù).當(dāng)γ,ε都大于零時(shí),(1.1)稱為粘性Boussinesq方程組,當(dāng)γ=ε=0時(shí),(1.1)稱為無(wú)粘Boussinesq方程組.
近年來(lái),有關(guān)Navier-Stokes方程組及Boussinesq方程組已有一些研究結(jié)果.文獻(xiàn)[1]給出了三維Navier-Stokes方程組的弱解在L2空間上的衰減估計(jì);文獻(xiàn)[2]給出了Navier-Stokes方程解的下界估計(jì);文獻(xiàn)[3-6]研究了Navier-Stokes方程時(shí)空衰減;文獻(xiàn)[7]給出了Boussinesq方程組弱解的L2衰減;文獻(xiàn)[8]討論了Boussinesq方程組的正則性問(wèn)題;文獻(xiàn)[9]研究了Boussinesq方程組的時(shí)空衰減.
本文假設(shè)γ=ε=1,即

2 預(yù)備知識(shí)
為研究Boussinesq方程當(dāng)n≥3時(shí)弱解的衰減率,需通過(guò)對(duì)逼近解序列作一致估計(jì),然后取極限得到.因此,先給出Boussinesq方程逼近解的構(gòu)造方法及相應(yīng)性質(zhì),其證明完全類似于文獻(xiàn)[10]中相關(guān)結(jié)果證明,故略去.
對(duì)于n≥3,考慮逼近解uk,θk,k=1,2,···,則有下列方程組:

其中
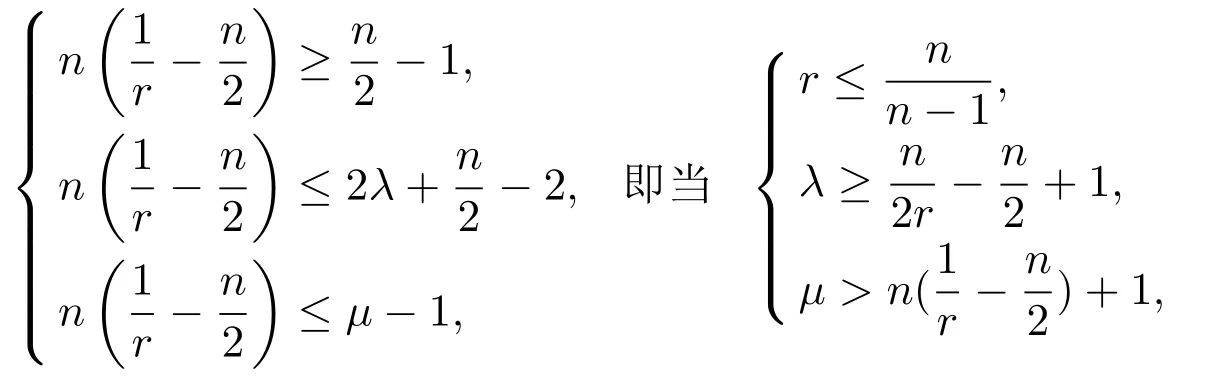
(1)P:Lr→,1 (2)uk∈L∞(0,T;)∩L∞(0,T;V),V是()在的閉包. (3)A=?P△,A是Navier-Stokes算子,A=λdE(λ)是A在的譜分解,其中{E(λ):λ≥0}是算子A的譜族. 對(duì)于方程(2.1)的逼近解,有如下性質(zhì)成立. 引理2.1(1)對(duì)于所有的T>0,方程(2.1)存在唯一弱解: (2)wk及其導(dǎo)數(shù)在×[0,T],T>0上是連續(xù)有界的,且滿足?·wk=0,對(duì)任意 (6)以下能量不等式成立: (7)對(duì)(1.1)式的第二個(gè)方程,有 證明在方程組(2.1)的第一個(gè)方程兩邊同時(shí)乘以u(píng)k,第二個(gè)方程兩邊同時(shí)乘以θk,并在?上積分,得 相加得, 由Growall不等式得, 引理2.2[10]?ρ>0,∥E(ρ)P(w·▽)u∥2≤cρn+24∥w∥2∥u∥2,其中c與u,w,ρ無(wú)關(guān). 定理3.1設(shè)若 則問(wèn)題(1.1)存在弱解u,θ,對(duì)于n≥3,有 為證明上述定理,先考慮問(wèn)題(2.1)光滑解的衰減估計(jì),再對(duì)(2.1)所構(gòu)造的逼近解進(jìn)行衰減估計(jì),通過(guò)取極限得到定理的證明.本文對(duì)逼近解序列(2.1)作衰減估計(jì),為書寫方便,記uk=u,θk=θ,wk=w,且得到的衰減估計(jì)關(guān)于k是一致的. 證明由能量不等式 可知,對(duì)于固定的ρ>0, 下證(3.2)的第一個(gè)式子.由Stokes算子的譜表示,有 (3.2)的第二個(gè)式子可類似得到.所以 為了估計(jì)(3.3)的右端,考慮(2.1)式的積分型: 由Minkowski不等式和引理2.2有: 由Gagliardo-Nirenberg不等式,有 即 類似可得, 這樣就有, 所以 同理可得, 由(3.4)-(3.7)式,得 同理可得, 將(3.8)式,(3.9)式代入(3.3)式,得 取ρ=αt?1,α>0,并在上面不等式的兩邊同乘以tα,得 關(guān)于t從0到t積分,并在所得不等式兩邊同除以tα,得 利用Stokes算子的(Lr?Lq)估計(jì),有 對(duì)于n≥3,取α充分大,由(3.11)式和(3.12)式及定理假設(shè),得 若 取ρ=αt?1,并在上面不等式的兩邊同乘以tα,得 若 [1]Soconbek M E.L2decay for weak solutions of the Navier-Stokes equations[J].Arch.Rat.Mech.Anal., 1985,88:209-222. [2]Soconbek M E.Lower bounds of rates of decay for solutions to the Navier-Stokes equations[J].Journal of the Ameerican Mathematical Society,1991,4(3):809-823. [3]He C.Weighted energy inequalities for nonstationary the Navier-Stokes equations[J].J.Dif f erential equation, 1998,148:422-444. [4]He C,Xin Z.On the decay properties of solutions to the non-stationaty Navier-Stokes equations in R3[J]. Proc.Roy.Soc.Edinburgh(Sect A),2001,131:597-619. [5]Bae H O,Jin B J.Temporal and spatial decays for the Navier-Stokes equations[J].Soc.Edinburgh(Sect A),2005,135:461-477. [6]Bae H O,Jin B J.Upper and lower bounds of temporal and spatial decays for the Navier-Stokes equations[J]. J.Dif f erential equation,2005,209:365-391. [7]劉穎.Boussinesq方程組弱解的L2衰減[D].北京:首都師范大學(xué)圖書館,2005. [8]李明杰.Boussinesq方程組解的正則性問(wèn)題研究[D].北京:首都師范大學(xué)圖書館,2006. [9]汪彩云.Boussinesq方程組時(shí)空衰減性質(zhì)研究[D].北京:首都師范大學(xué)圖書館,2006. [10]Borcherd W,Miyakawa T.L2decay for the Navier-Stokes f l ow in half spaces[J].Math.Ann.,1998,282:139-155. The L2decay of the weak solution of the Boussinesq equations in half space Liu Yanmei,Gao Qiaoqin This paper is mainly concerned with the L2decay the weak solution of the Boussinesq equations in half space under the appropriate assumption of the external force f.Frist the paper gives uniform L2decay estimate of smooth solution under the assumption that the solution is smooth.Then the paper construcs approximate solution and gives uniform decay estimate of the approximate solution.Finally,the theorem is proved by taking limit. Boussinesq equations,weak solution,L2decay O175.2 A 1008-5513(2014)06-0587-08 10.3969/j.issn.1008-5513.2014.06.007 2014-09-01. 山西省教育廳教學(xué)改革項(xiàng)目(J2011101). 劉艷梅(1978-),碩士,講師,研究方向:微分方程. 2010 MSC:38Q80




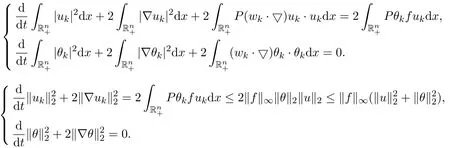


3 主要結(jié)果




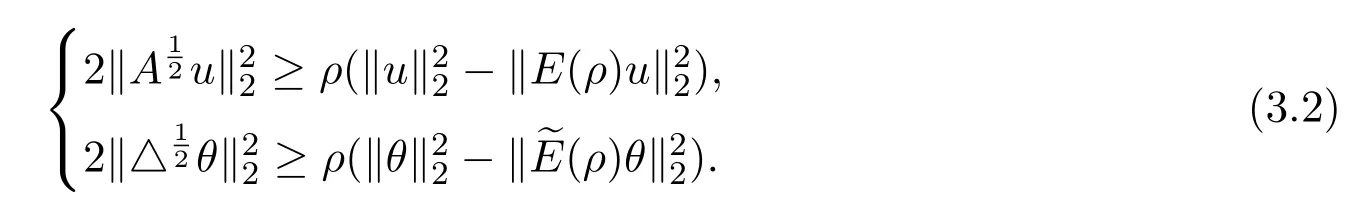



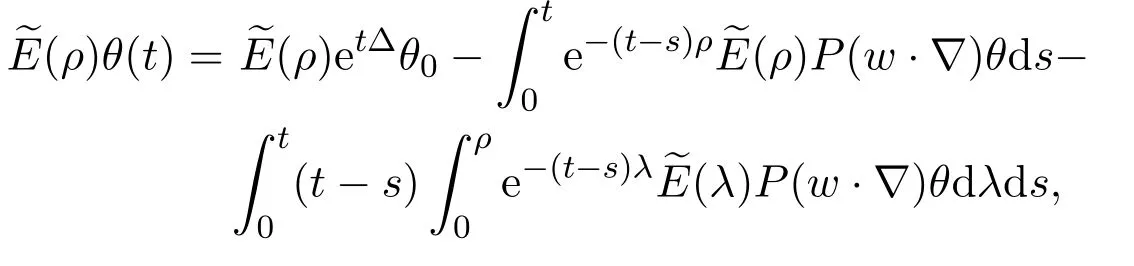
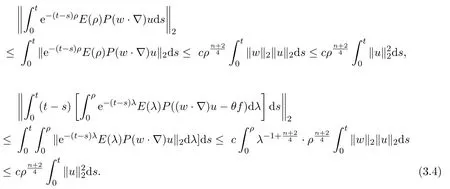




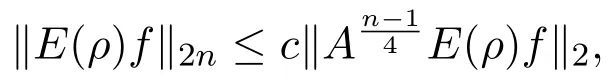
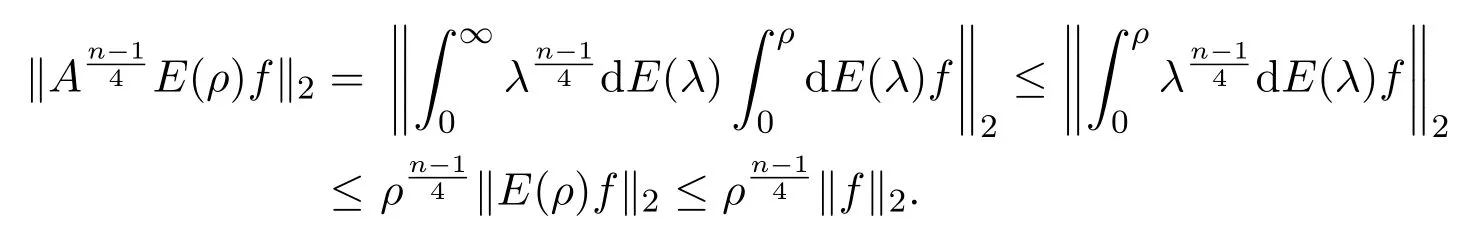
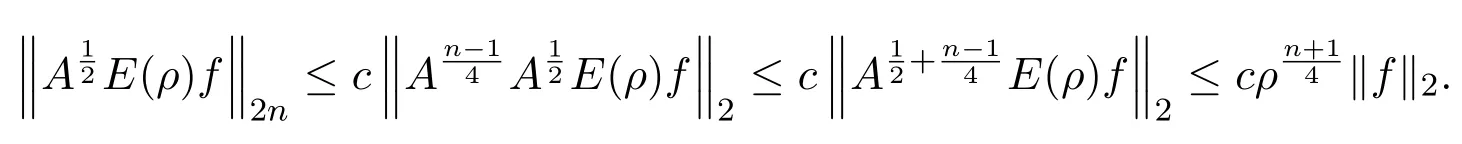
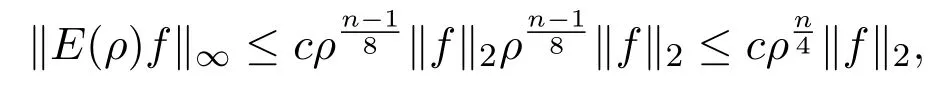



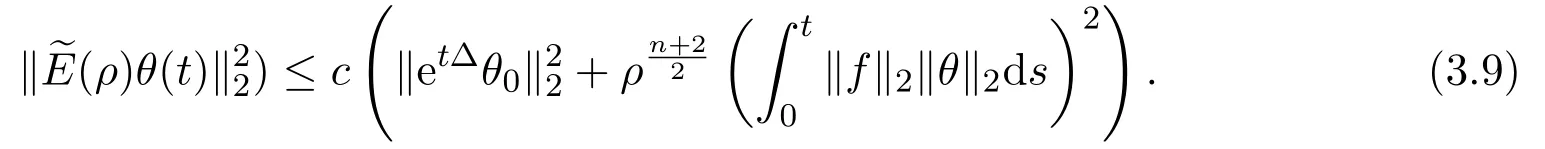



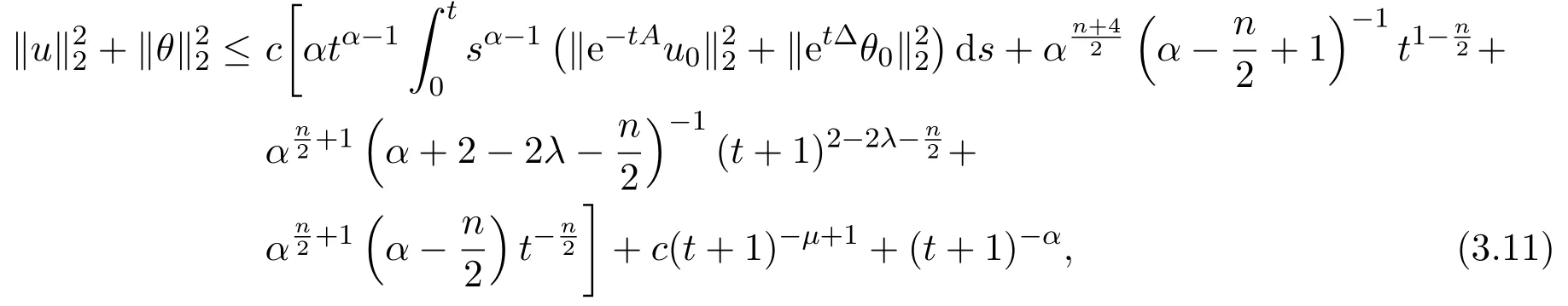



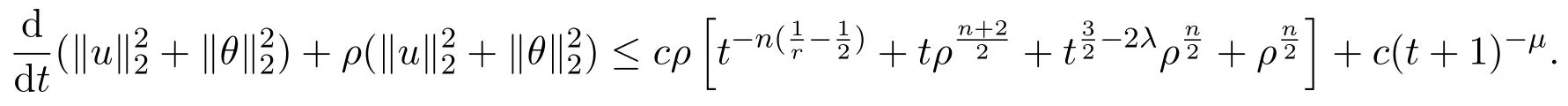


(Department of Mathematics,Lvliang College,Lishi033000,China)

