楊標(biāo)桂,朱晴晴

(福建師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院,福建福州350108)

近Kaehler流形S3×S3上的殆切觸拉格朗日子流形

楊標(biāo)桂,朱晴晴

(福建師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院,福建福州350108)

對(duì)于近Kaehler流形S3×S3上的一個(gè)拉格朗日子流形M,給出由M上的一個(gè)單位向量場(chǎng)典范引出的殆切觸度量結(jié)構(gòu)是α-Sasakian的充要條件.當(dāng)這個(gè)殆切觸度量結(jié)構(gòu)為切觸度量結(jié)構(gòu)時(shí),給出了這個(gè)切觸度量結(jié)構(gòu)是Sasakian結(jié)構(gòu)的充分必要條件.關(guān)鍵詞：近Kaehler流形;拉格朗日子流形;(殆)切觸度量結(jié)構(gòu);Sasakian結(jié)構(gòu)

1 引言

1970年,文獻(xiàn)[1]系統(tǒng)地研究了近Kaehler流形,這些近Kaehler流形是帶有復(fù)結(jié)構(gòu)J的殆Hermitian流形,這里張量場(chǎng)ˉ?J是反對(duì)稱的.近Kaehler 6維球面S6的子流形已被許多人研究過(guò)(參見(jiàn)文獻(xiàn)[2-4]).近年來(lái),文獻(xiàn)[5]中闡述了齊性6維近Kaehler流形只包括近Kaehler流形S3×S3,射影空間CP3和旗流形SU(3)/U(1)×U(1),這些空間都是緊致的3維對(duì)稱空間.眾所周知,一般情況下近Kaehler流形的子流形分為殆復(fù)子流形和全實(shí)子流形,而拉格朗日子流形為全實(shí)子流形的一種.文獻(xiàn)[6]系統(tǒng)地介紹了近Kaehler流形S3×S3的殆復(fù)曲面,本文將初步研究S3×S3的殆切觸拉格朗日子流形.旨在找出由S3×S3的拉格朗日子流形上的一個(gè)單位向量場(chǎng)典范引出的殆切觸度量結(jié)構(gòu)是α-Sasakian的充要條件,并且討論這個(gè)殆切觸子流形為切觸子流形時(shí)的情形.

2 預(yù)備知識(shí)

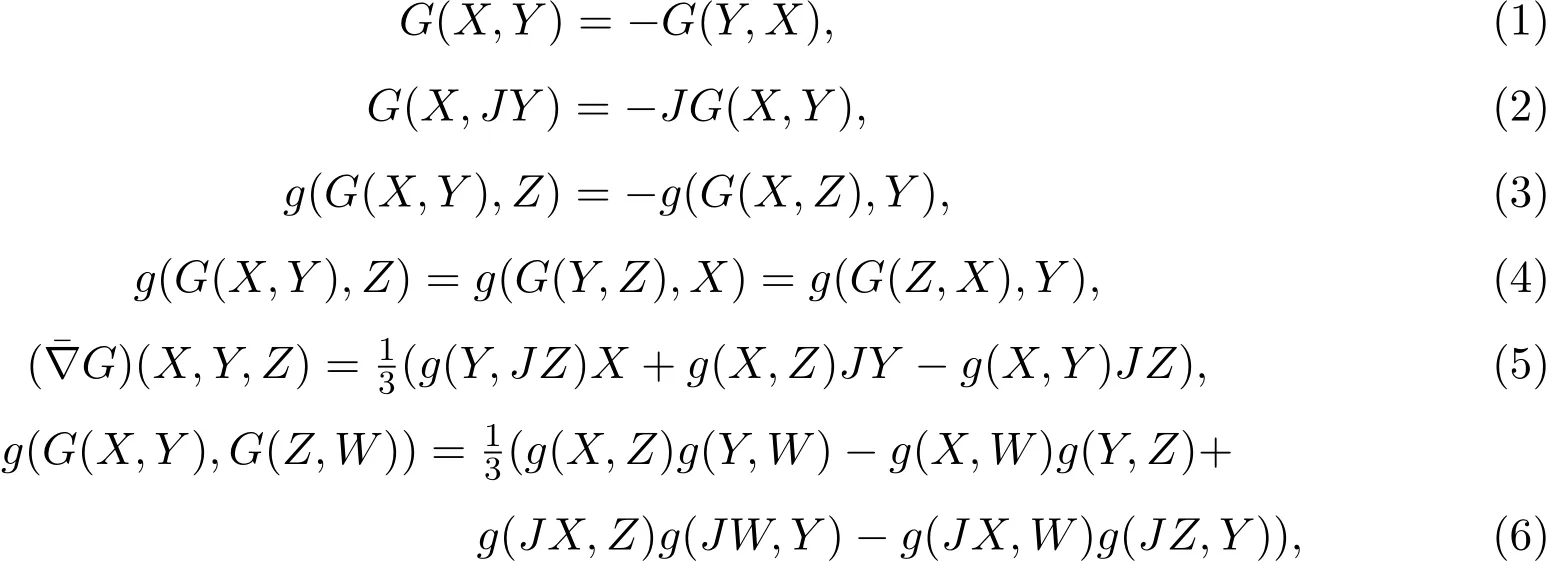
其中X,Y∈TM,ξ∈T⊥M.第二基本形式σ和形狀算子Aξ之間有如下關(guān)系式:

回顧殆切觸度量流形的相關(guān)知識(shí)[7-8].一個(gè)(2n+1)維光滑流形M稱為殆切觸度量流形,若?X,Y∈TM,M上存在一個(gè)整體1形式η,一個(gè)單位向量場(chǎng)ξ,一個(gè)(1,1)-型張量場(chǎng)φ和黎曼度量g滿足下列方程:

顯然

若滿足dη(X,Y)=g(X,φY),則M上的殆切觸度量結(jié)構(gòu)(M,η,,g)稱為切觸度量結(jié)構(gòu).

當(dāng)h=0時(shí),稱為K-切觸度量流形.殆切觸度量流形若滿足(?Xφ)Y=α(g(X,Y)ξ?η(Y)X),則稱為α-Sasakian流形,其中?是關(guān)于g的黎曼聯(lián)絡(luò).特別地,若α=1,這個(gè)切觸度量流形就是Sasakian流形.切觸度量流形是K-切觸度量流形當(dāng)且僅當(dāng)Ric(X,ξ)=2nη(X).在維數(shù)為3的情況下,K-切觸條件等價(jià)于Sasakian條件.

3 主要結(jié)果

首先,給出如下引理.

引理3.1設(shè)M為S3×S3的一個(gè)拉格朗日子流形,?X,Y∈TM,有G(X,Y)∈T⊥M.

證明由(7)式和(8)式可得:

其中X,Y,Z∈TM.(1)式和(3)式表明上式右邊互相相等.因此有g(shù)(G(X,Y),Z)=0,這表明G(X,Y)正交于M.

其次,有如下結(jié)果.

引理3.2設(shè)M為S3×S3的一個(gè)拉格朗日子流形,?X,Y,Z∈TM,有

證明由(1)式和(2)式知,?X,Y,Z∈TM,有

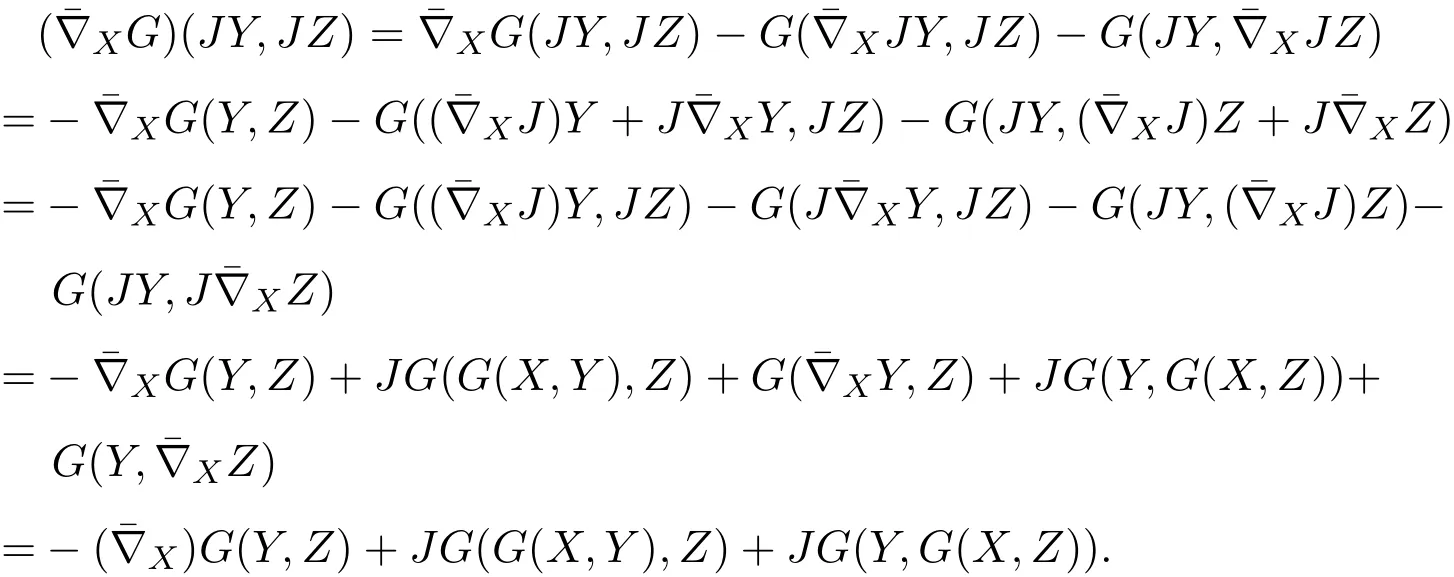
結(jié)合(5)式,得到

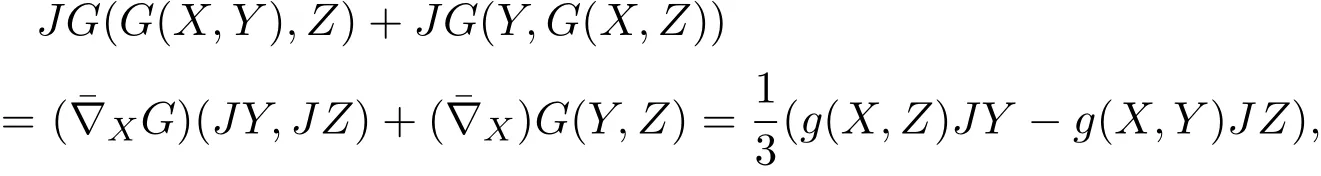
即

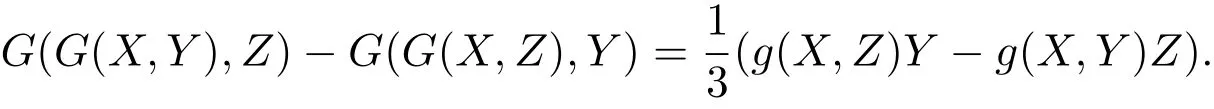
因此

或者等價(jià)于

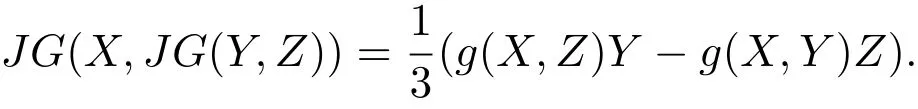
再次,令ξ是M上的一個(gè)單位向量場(chǎng),遵從M上的度量g,定義一個(gè)1形式η滿足η(X)=g(X,.由(2)式可知,?X∈TM,向量場(chǎng)G(X,J)=?JG(X,),由引理3.1可知,G(X,J)∈TM.因此給出如下引理:

引理3.3的拉格朗日子流形(M,g)上的一個(gè)單位向量場(chǎng)ξ,引出一個(gè)典范殆切觸度量結(jié)構(gòu)(φ,g,),其中結(jié)構(gòu)張量φ定義為

證明由定義知φ(ξ)=0,從(1)式和(2)式可以得到,對(duì)?X,Y∈TM,有

另外

結(jié)合引理3.2,可得

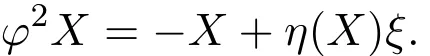
又由(6)式得到,

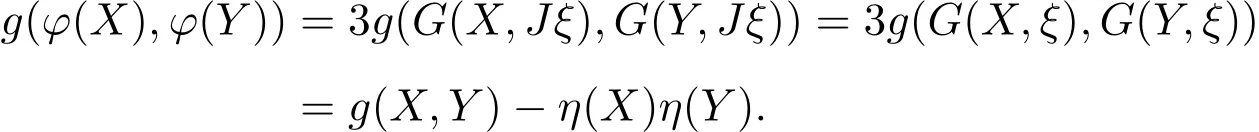
給出如下定義:

定義3.1(φ,,η,g)稱為M上的典范殆切觸度量結(jié)構(gòu),其中單位向量場(chǎng)由上述引理定義.

定理3.1令M為的一個(gè)拉格朗日子流形,帶有近Kaehler結(jié)構(gòu)(g,J),是M上的一個(gè)單位向量場(chǎng),帶有典范引出的M上的殆切觸度量結(jié)構(gòu)(φ,g,),則這個(gè)結(jié)構(gòu)是的當(dāng)且僅當(dāng)F=0.

證明由引理3.3,計(jì)算出φ的共變導(dǎo)數(shù)

將(5)式和(8)式代入上式,得

通過(guò)比較上述等式左右兩端的切向分量,有

可知,若F=0,則

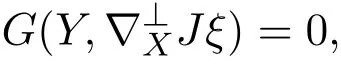
即

用ξ代替Y,可得φFX=0.等式兩邊用φ作用便得F=0.

此外，還可以得到如下結(jié)果:

定理3.2令M為的一個(gè)拉格朗日子流形,帶有近Kaehler結(jié)構(gòu)(g,J),是M上的一個(gè)單位向量場(chǎng).假設(shè)由典范引出的M 上的殆切觸度量結(jié)構(gòu)(φ,g,)是切觸度量結(jié)構(gòu),

證明由(7)式-(8)式和引理3.3可得,

成立.因此就有

又由文獻(xiàn)[8]知:div(hφ)(X)=Ric(ξ,X)?2η(X).得

[1] Gray A.Nearly Kaehler manifolds[J].J.Di ff.Geom.,1970,4:283-309.

[2] Deshmukh S,EI Hadi K.A Sasakian structure on a 3-dimensional totally real submanifold of the nearly Kaehler 6-sphere[J].Panamer Math.J.,1992,3:43-52.

[3] Dillen F,Opozda B,Verstraelen L,et al.On totally real 3-dimensional submanifold of the nearly Kaehler 6-sphere[J].Proc.Am.Math.Soc.,1987,99:741-749.

[4] Ejiri N.Totally real submanifolds in a 6-sphere[J].Proc.Am.Math.Soc.,1981,83:759-763.

[5] Butruille J.B.Homogeneous nearly Kaehler manifolds.Handbook of Pseudo-Riemannian Geometry and Supersymmetry[M].IRMA Lect.Math.Theor.Phys.,16,Eur.Math.Soc.,Zu¨rich,2010.

[6] Bolton J,Dillen F,Dioos B,et al.Almost complex surfaces in the nearly kaehler S3×S3[J].ArXiv:1208. 0737.Preprint,2013.

[7] Blair D.E.Riemannian Geometry of Contact and Symplectic Manifolds[M].Sec.edi.Progress in Mathematics,203.,Boston,MA:Birkh¨auser Boston,Inc,2010.

[8] Blair D.E,Sharma R.Generalization of Myers′theorem on a contact manifold[J].Illinois Journal of Mathematics,1990,34:837-844.

Almost contact Lagrangian submanifolds of nearly Kaehler

Yang Biaogui,Zhu Qingqing
(School of Mathematics and Computer Science,Fujian Normal University,Fuzhou350108,China)

For a Lagrangian submanifold of the nearly Kaehler S3×S3,we provide a necessary and sufficient condition for a canonically induced almost contact metric structure by a unit vector fi eld,to be α-Sasakian. Furthermore,assuming the almost contact metric structure is contact metric structure,we give a necessary and sufficient condition in which the contact metric structure is Sasakian.

nearly Kaehler manifold,Lagrangian submanifold,(almost)contact metric structure, Sasakian structure

O186

A

1008-5513(2014)05-0454-06

10.3969/j.issn.1008-5513.2014.05.003

2014-07-26.

國(guó)家自然科學(xué)基金(11171139,11326045,11401099);福建省自然科學(xué)基金(2011J05001);福建省教育廳A類(lèi)項(xiàng)目(JA11052).

楊標(biāo)桂(1976-),博士,副教授,研究方向:微分幾何.

2010 MSC:53D15