包晶晶[1,2],斯琴其木格[3],楊元生[1,4],吉日木圖[1,2]

(1.內(nèi)蒙古民族大學離散數(shù)學研究所,內(nèi)蒙古通遼028043; 2.內(nèi)蒙古民族大學數(shù)學學院,內(nèi)蒙古通遼028043;

3.赤峰學院計算機學院,內(nèi)蒙古赤峰024000;

4.大連理工大學計算機科學與技術學院,遼寧大連116024)

包晶晶[1,2],斯琴其木格[3],楊元生[1,4],吉日木圖[1,2]

(1.內(nèi)蒙古民族大學離散數(shù)學研究所,內(nèi)蒙古通遼028043; 2.內(nèi)蒙古民族大學數(shù)學學院,內(nèi)蒙古通遼028043;

3.赤峰學院計算機學院,內(nèi)蒙古赤峰024000;

4.大連理工大學計算機科學與技術學院,遼寧大連116024)

摘要：研究了有向圖?的優(yōu)美性,利用搜索圖的標號的算法與數(shù)學證明相結合的方法,證明了有向圖??→為優(yōu)美圖,其中n為任意正整數(shù).

關鍵詞：有向圖;有向圈;優(yōu)美圖;優(yōu)美標號

1 引言

設G=(V,E)為有向圖,如果存在單射θ:V(G)?→{0,1,2,···,|E|},使得誘導映射θ′:E(G)?→{1,2,···,|E|}是雙射,其中對任意的邊uv∈E(G),有

則θ稱為有向圖G=(V,E)的優(yōu)美標號,θ′稱為有向圖G=(V,E)的邊優(yōu)美標號.用表示有n(≥3)個頂點的有向圈,表示m個無公共頂點的有向圈之并.目前,關于有向圈相關圖的優(yōu)美性的研究結果有m(見文獻[1-2])和m?(見文獻[3-4])為優(yōu)美圖.關于有向圖的優(yōu)美性的結論有見文獻[5])和(見文獻6])是優(yōu)美圖.文獻[7]給出:有向圖優(yōu)美的必要條件為mn≡0(mod 2),并提出猜想:當mn≡0(mod 2)時,有向圖為優(yōu)美圖.本文給出了有向圖是優(yōu)美圖,其中n為任意正整數(shù).

2 主要結果

定理2.1當n≡0(mod 2)時,有向圖為優(yōu)美圖.

證明設有向圖的四個有向圈為頂點依次為:

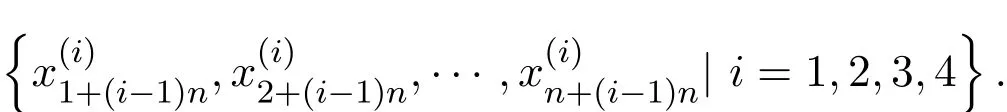
情形1當n≡0(mod 4)時,的頂點標號定義如下:

情形2當n≡2(mod 4)時,的頂點標號定義如下:

其次證明,情形1中頂點標號所誘導的邊標號θ′是E()到{1,2,···,4n}的一一映射.

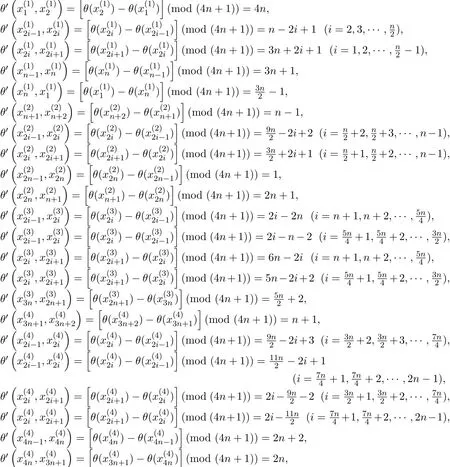
由上可知,取值為偶數(shù)的邊標號有:

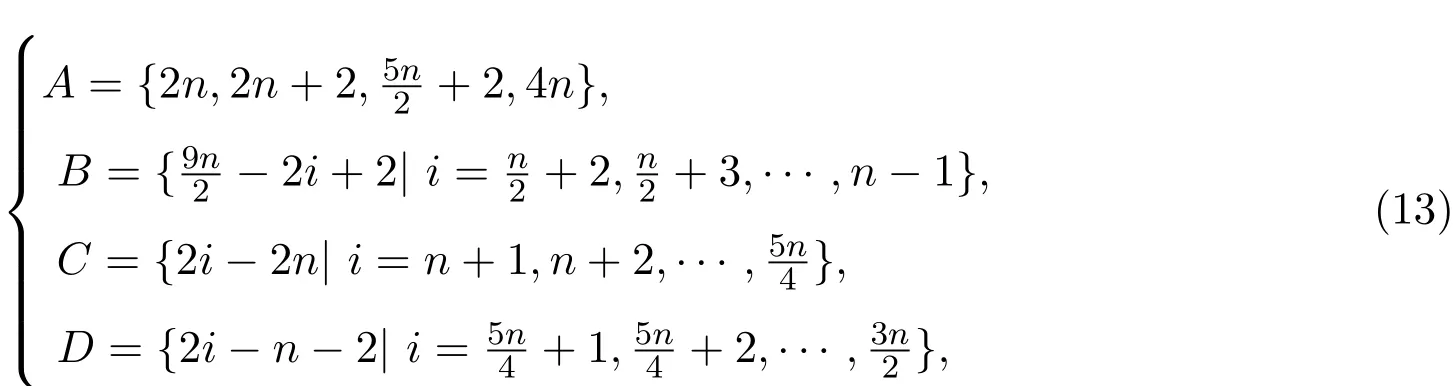
其中

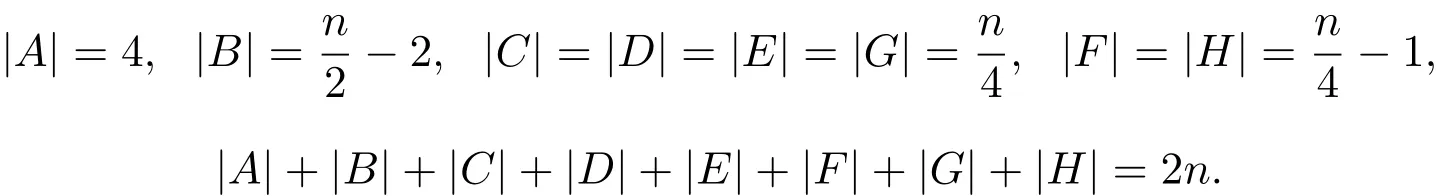
由以上的討論可知,A,B,C,D,E,F,G,H中的數(shù)彼此不相同,從而得知取值為偶數(shù)的邊標號集合為{2,4,···,4n}.同理,取值為奇數(shù)的邊標號集合為{1,3,···,4n?1}.所以θ′是到{1,2,···,4n}的一一映射.故上述θ為優(yōu)美標號.

類似情形1的方法,在情形2中定義θ所確定的頂點標號集為{0,1,2,···,4n}?{n},θ所誘導的θ′是E()到{1,2,···,4n}的一一映射.故θ為優(yōu)美標號.

定理2.2當n≡1(mod 2)時,有向圖為優(yōu)美圖.

證明設有向圖4?→Cn的四個有向圈為{)|i=1,2,3,4},頂點依次為

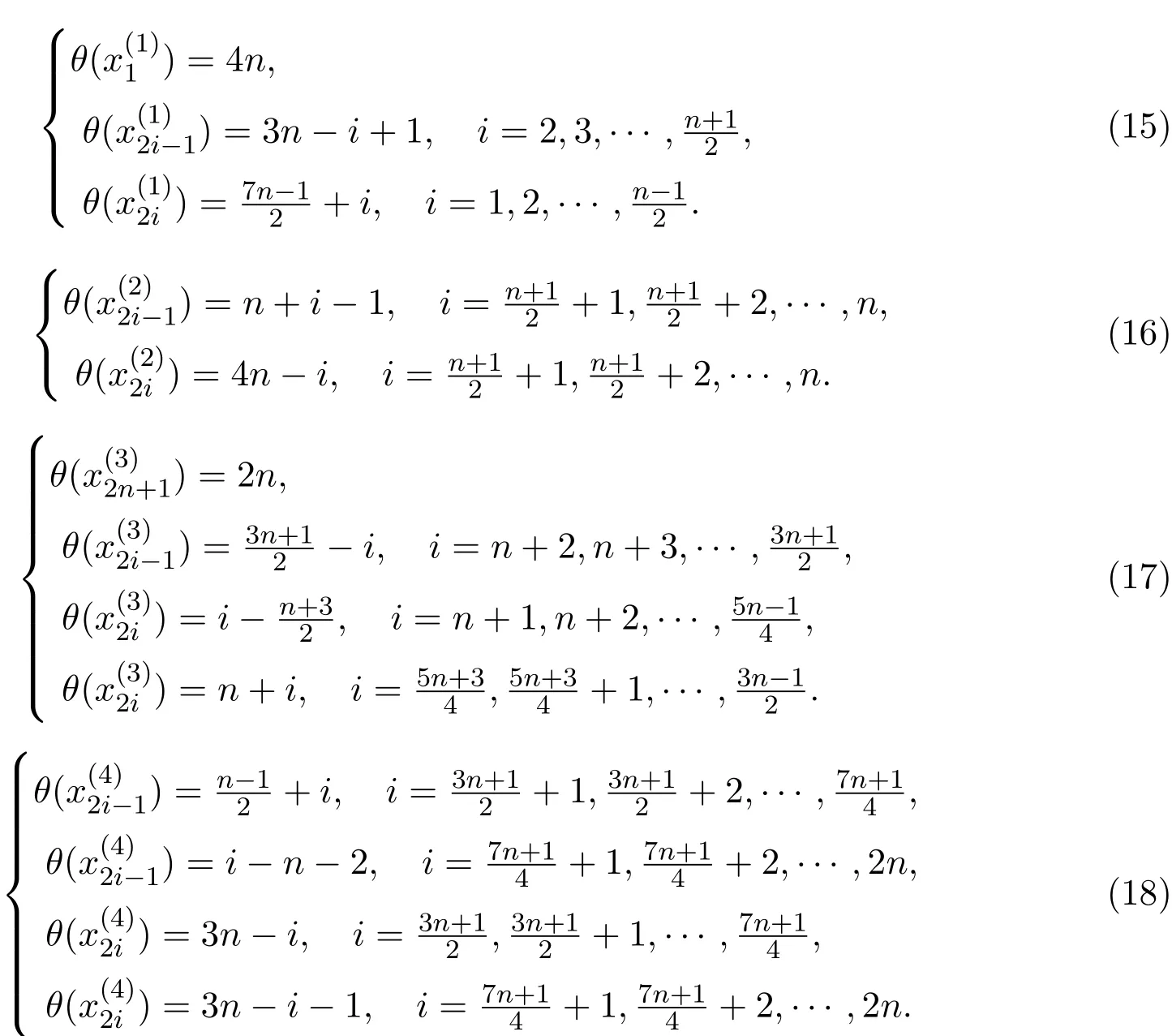
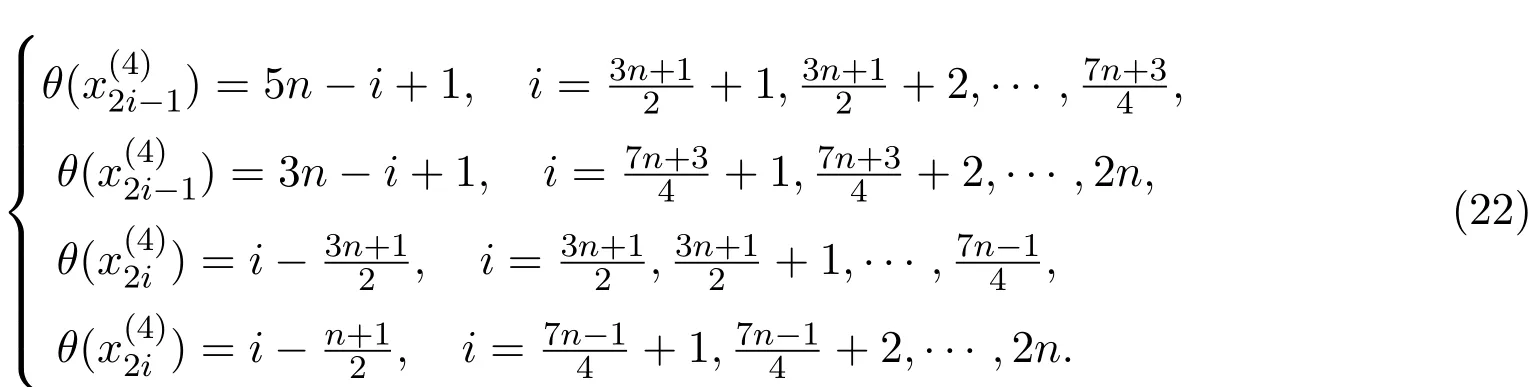
類似于定理2.1的證明方法,在情形(1),情形(2)中定義的θ均為優(yōu)美標號.

參考文獻

[1] Jirimutu,Xu Xirong,Feng Wei,et al.Proof of a conjecture on the gracefulness of a digraph[J].Utilitas Mathematica,2010,81:255-264.

[3] Zhao L,Jirimutu,Xu X,et al.On the gracefulness of the digraphs n?for m odd.[J].J Prime Res. Math.,2008,4:118-126.

[4] Hegde S M,Shivarajkumar.Two conjectures on graceful digraphs[J].Graphs and Combinatorics,2013,29:933-954.

[7] 馬克杰.優(yōu)美圖[M].北京:北京大學出版社,1991.

2010 MSC:05C69

中圖分類號：O157.5

文獻標識碼：A

文章編號：1008-5513(2014)05-0543-08

DOI：10.3969/j.issn.1008-5513.2014.05.016

收稿日期：2014-04-03.

基金項目：國家自然科學基金(61262018).

作者簡介：包晶晶(1989-),碩士生,研究方向：圖論及其應用.

On the Gracefulness of the Digraph

Bao Jingjing[1,2],Siqinqimuge[4],Yang Yuansheng[1,3],Jirimutu[1,2]
(1.Institute of Discrete Mathematics,Inner Mongolia University for Nationalities,Tongliao028043,China; 2.College of Mathematics,Inner Mongolia University for Nationalities,Tongliao028043,China; 3.College of Computer,Chifeng University,Chifeng024000,China; 4.College of Computer Science and Technology,Dalian University of Technology,Dalian116024,China)

Abstract:This paper researches the gracefulness of digraph m?→Cn.By utilizing algorithm of searching for graph labeling and combining with mathematical proof,this paper proves that digraph 4?→Cnis graceful for any positive integer n.

Key words:digraph,directed cycles,graceful graph,graceful labeling