ZHANG Zu jin

SchoolofM athematicsand Computer Sciences,Gannan NormalUniversity, Ganzhou 341000,China.

Liquid Crystal Flow sw ith Regu larity in One D irection

ZHANG Zu jin?

SchoolofM athematicsand Computer Sciences,Gannan NormalUniversity, Ganzhou 341000,China.

Received 7 February 2014;Accep ted 9M ay 2014

.In this paper,w e consider the Cauchy p roblem for them odelof liquid crystal.We show that if the velocity field u satisfies then the solution is in factsm ooth.

Liquid crystals;regu larity criteria.

1 In troduction

In this paper,w e consider the follow ing m odel of liquid crystal in R3introduced by Lin[33]:

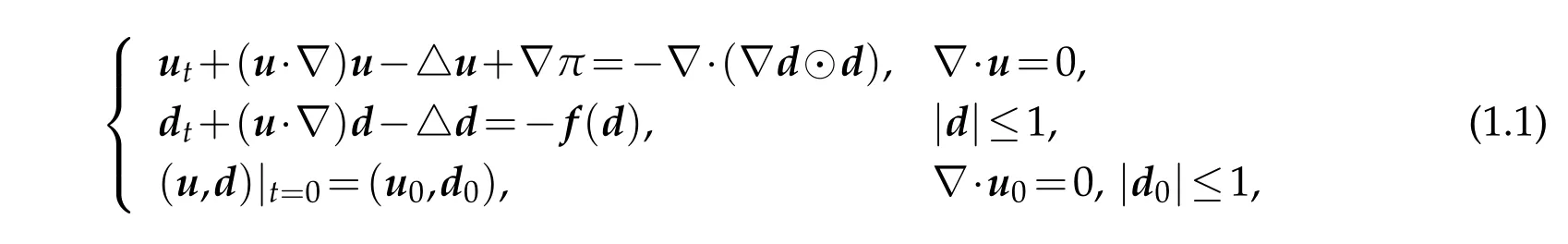
w here u=(u1,u2,u3)is the fluid velocity field,d=(d1,d2,d3)is the(averaged)m acroscopic/continuum m olecu le orientation,πis a scalar p ressure,u0and d0are the p rescribed initial data,

Hereand thereafter,w e use the summ ation convention that repeated ind icesare summ ed au tom atically over{1,2,3}.

The existence of a global-in-tim e w eak solution and the local unique strong solution hasbeen established by Lin and Liu[1].Bu tas for the incom p ressible Navier-Stokessystem(d is constant in(1.1)),w hether a given globalw eak solu tion is regu lar and w hether the localunique strong solu tion can exist globally are challenging open p roblem s.

M otivated by the regu larity criteria for the Navier-Stokes[2–13]and MHD equations[14–26],som e au thors considered the regu larity cond itions for(1.1),see[27–32]and references cited therein.

In this paper,w ew ou ld like to im p rove the regu larity criterion

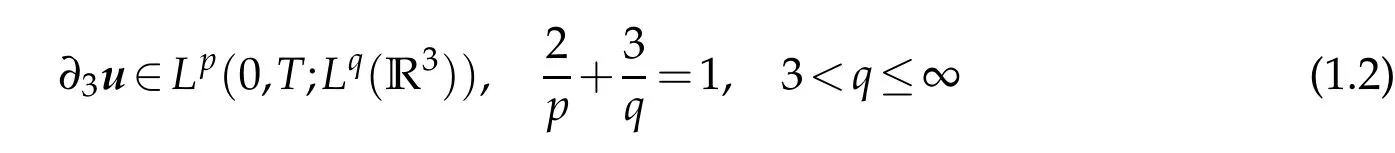
established in[29].

Beforew e state the p recise resu lt,letus recall thew eak form u lation of(1.1).

Definition 1.1([1]).Ameasurablepair(u,d)issaid tobeaweak solution of(1.1)on[0,T]×R3, provided thefollow ing assertionshold:

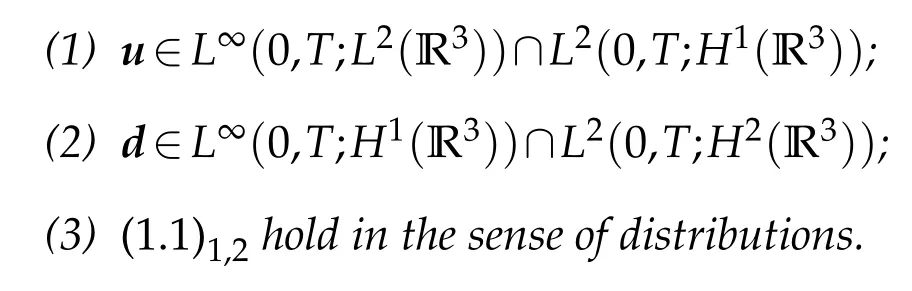
Now ou rm ain resu lt reads:

Theorem 1.1.Let u0∈L2(R3)satisfy?·u0=0,d0∈H1(R3)w ith|d0|≤1,and let themeasurable pair(u,d)bea given weak solution of(1.1)w ith initial data(u0,d0).If

then the solution is in fact strong,and thus classical.

By a strong solu tion,w em ean(u,d)satisfy

Rem ark 1.1.Notice that

the scaling d im ension of Theorem 1.1 can alm ostachieve 3/2.

2 Proof of Theorem 1.1

In this section,w e shallp rove Theorem 1.1.First,letus recall

Taking the inner p roduct of(1.1)1,(1.1)2w ith-△u,△2d in L2(R3)respectively,w e obtain

Com bining(2.1)and(2.2),w e deduce

Gathering(2.4),(2.5)and(2.6)in to(2.3),w e obtain

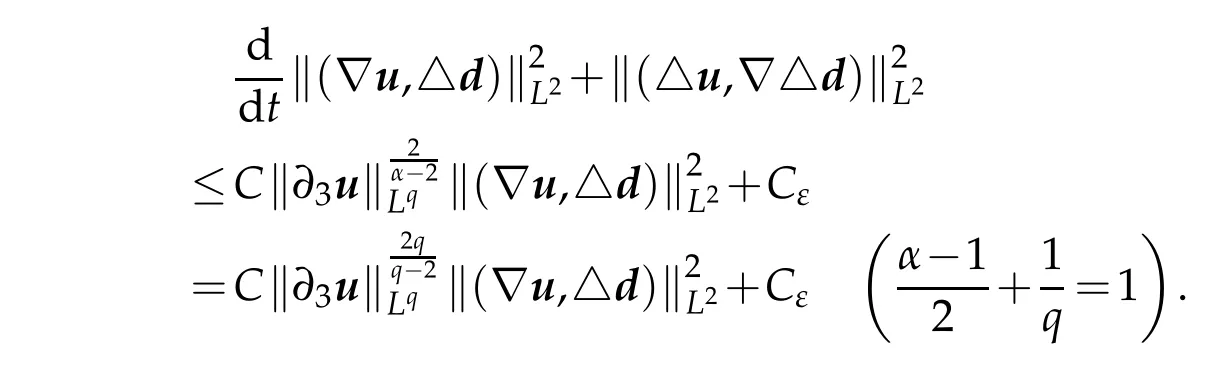
App lying Gronw all inequality,w e deduce that the solu tion pair(u,d)isa strong solu tion, as desired.

The p roofof Theorem 1.1 is com p leted.

Acknow ledgm en ts

Thisw ork w as partially supported by the Youth Natural Science Foundation of Jiangxi Province(20132BAB211007),theNationalNatu ralScience Foundation ofChina(11326138), and the Science Foundation of JiangxiProvincial Departm entof Education(GJJ14673).

[1]Lin F.H.,Liu C.,Nonparabolic d issipative system sm odeling the flow of liquid crystals. Comm.Pure Appl.M ath.,48(1995),501-537.

[3]Cao C.S.,Su fficientconditions for the regu larity to the 3D Navier-Stokesequations.Discrete Contin.Dyn.Syst.,26(2010),1141-1151.

[4]Cao C.S.,TitiE.S.,G lobal regu larity criterion for the 3D Navier-Stokesequations involving one entry of the velocity grad ient tensor.Arch.RationalM ech.Anal.,202(2011),919-932.

[5]Kukavica I.,Ziane M.,One com ponent regu larity for the Navier-Stokes equations.Nonlinearity,19(2006),453-469.

[6]Kukavica I.,Ziane M.,Navier-Stokes equations w ith regu larity in one d irection.J.M ath. Phys.,48(2007),065203,10 pp.

[7]Neustupa J.,Novotn′y A.,Penel P.,An interior regu larity of a w eak solu tion to the Navier-Stokesequations in dependenceon one com ponentof velocity,Topics inm athem atical fluid m echanics.Quad.M at.,10(2002),163-183.

[8]Zhang Z.J.,A Serrin-type regu larity criterion for the Navier-Stokesequations via one velocity com ponent.Commu.Pure Appl.Anal.,12(2013),117-124.

[9]Zhang Z.J.,Yao Z.A.,LiP.,Guo C.C.,Lu M.,Tw o new regu larity criteria for the 3D Navier-Stokesequations via tw o entriesof the velocity gradient tensor.Acta Appl.M ath.,123(2013), 43-52.

[10]Zhang Z.J.,Yao Z.A.,Lu M.,N iL.D.,Som e Serrin-type regu larity criteria forw eak solutions to the Navier-Stokesequations.J.M ath.Phys.,52(2011),053103.

[11]Zhou Y.,A new regu larity criterion for w eak solu tions to the Navier-Stokes equations.J. M ath.Pures Appl.,84(2005),1496-1514.

[12]Zhou Y.,Pokorn′y M.,On a regu larity criterion for the Navier-Stokes equations involving grad ientofone velocity com ponent.J.M ath.Phys.,50(2009),123514,11 pp.

[13]Zhou Y.,Pokorn′y M.,On the regu larity of the solutions of the Navier-Stokes equations via one velocity com ponent.Nonlinearity,23(2010),1097-1107.

[14]Cao C.S.,Wu J.H.,Tw o new regu larity criteria for the 3D MHD equations.J.D ifferential Equations,248(2010),2263-2274.

[15]Chen Q.L.,M iao C.X.,Zhang Z.F.,On the regu larity criterion ofw eak solution for the 3D viscousm agneto-hyd rodynam icsequations.Comm.M ath.Phys.,284(2008),919-930.

[16]Chen Q.L.,M iao C.X.,Zhang Z.F.,The Beale-Kato-M ajda criterion for the 3D m agnetohyd rodynam ics equations.Comm.M ath.Phys.,275(2007),861-872.

[17]He C.,Wang Y.,On the regu larity criteria forw eak solu tions to them agnetohyd rodynam ic equations.J.Differential Equations,238(2007),1-17.

[18]HeC.,Xin Z.P.,On the regu larity ofw eak solutions to them agnetohyd rodynam icequations. J.Differential Equations,213(2005),235-254.

[19]Jia X.J.,Zhou Y.,A new regu larity criterion for the 3D incom p ressible MHD equations in term sof one com ponentof the grad ientof p ressu re.J.M ath.Anal.Appl.,396(2012),345-350.

[20]Jia X.J.,Zhou Y.,Regu larity criteria for the 3D MHD equations involving partial com ponents.(2011),doi:10.1016/j.nonrw a.2011.07.055.

[21]Jia X.J.,Zhou Y.,Regu larity criteria for the 3DMHD equations via partialderivatives.Kinet. Relat.M odels,5(2012),505-516.

[22]Wang W.D.,Zhang Z.F.,Lim iting case for the regu larity criterion to the 3D M agnetohyd rodynam ics equations.J.D ifferential Equations,252(2012),5751-5762.

[23]Zhang Z.J.,Rem arkson the regu larity criteria forgeneralized MHD equations.J.M ath.Anal. Appl.,375(2011),799-802.

[24]Zhang Z.J.,LiP.,Yu G.H.,Regu larity criteria for the3D MHD equationsvia one directional derivative of the p ressu re.J.M ath.Anal.Appl.,401(2013),66-71.

[25]Zhou Y.,Rem arks on regu larities for the 3D MHD equations.Discrete Contin.Dyn.Syst.,12 (2005),881-886.

[26]Zhou Y.,Gala S.,A new regu larity criterion forw eak solutions to theviscousMHD equations in term sof the vorticity field.Nonlinear Anal.,72(2010),3643-3648.

[27]Fan J.S.,Ozaw a T.,Regu larity criterion for the 3D nem atic liquid crystal flow s.ISRN M ath. Anal.,2012(2012),935045.

[28]Gala S.,Liu Q.,Ragusa M.A.,A new regu larity criterion for nem atic liquid crystal flow s. Appl.Anal.,(2011),doi:10.1080/00036811.2011.581233.

[29]Liu Q.,Zhao J.H.,CuiS.B.,A regu larity criterion for the three-dim ensionalnem atic liquid crystal flow in term of one d irectional derivative of the velocity.J.M ath.Phys.,52(2011), 033102.

[30]Liu Q.,Zhao J.H.,Cui S.B.,Logarithm ically im p roved BKM’s criterion for the 3D nem atic liquid crystal flow s.Nonl.Anal.,75(2012),4942-4949.

[31]Zhang Z.J.,Wang X.F.,Yao Z.A.,Rem arks on regu larity criteria for thew eak solutions of liquid crystals.J.Evol.Equ.,12(2012),801-812.

[32]Zhou Y.,Fan J.S.,A regu larity criterion for the nem atic liquid crystal flow s.J.Inequ.Appl., 2010(2010),589697.

[33]Lin F.H.,Nolinear theory of defects in nem atic liquid crystals:phase transition and flow phenom ena.Comm.PureAppl.M ath.,42(1989),789-814.

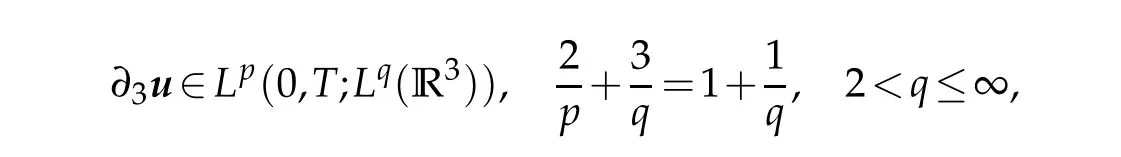
10.4208/jpde.v27.n3.5 Sep tem ber 2014

?Correspond ing au thor.Emailaddress:zhangzuj in361@163.com(Z.Zhang)

AM SSub jectClassifications:35Q 35,76B03

Chinese Library Classifications: O175.28,O175.29