CHEN Yi-Xiang(陳翼翔)

School of Electronics Information,Zhejiang University of Media and Communications,Hangzhou 310018,China

1 Introduction

The optical solitons[1?2]are now considered to have a potential application to long-distance communication and all-optical ultrafast switching devices since they can maintain the overall shapes.If they allow their amplitudes and(or)widths changing with the modulation of system’s parameters such as the dispersion,nonlinearity,gain,inhomogeneity,etc.,these solitons are called self-similar solitons(similaritons).[3?5]If the amplitude of wave is more times higher than the average wave crests,these waves are called rogue waves.[6?7]

Recently,some research works for spatial localized solutions in(2+1)-dimensional(2D)nonlinear Schr¨odinger equation(NLSE)have been carried out.[8?10]Although spatial soliton solutions are usually unstable for 2D constant-coeきcient NLSE due to the weak and strong collapses,[11]some stable spatial localized solutions for 2D variable-coeきcient NLSE were reported.[9,12?13]However,in previous works,spatial solitons for diあerent distributed transverse diあraction are hardly discussed.Moreover,the dynamical behaviors for spatial solitons in different diあraction decreasing waveguides(DDWs)with the hyperbolic,Gaussian and Logarithmic prof i les are hardly investigated.

In this paper,the above issues are studied via a systematic analysis based on the similarity transformation for the inhomogeneous(2+1)-dimensional NLSE with different distributed transverse diあractions as follows

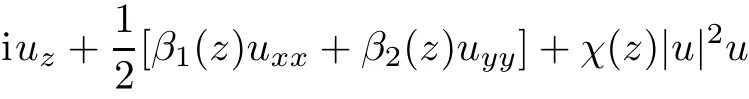
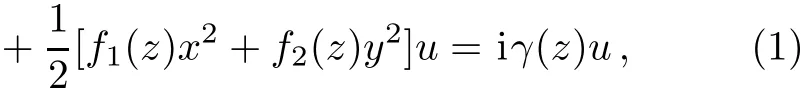
where u(z,x,y)is the complex envelope of the electrical f i eld in the moving frame,z is the coordinate along the propagation direction of the carrier wave.The functions β1(z)and β2(z)represent the diあraction coeきcients for diあerent transverse coordinates(x,y), χ(z)the selffocusing(χ ＞ 0)or the self-defocusing(χ ＜ 0)nonlinearity coeきcient,and γ(z)the gain(γ ＞ 0)or the loss(γ ＜ 0)coeきcient.This model describes the propagation of optical beam inside the 2D graded-index waveguide amplif i er with refractive index n=n0+n1[f1(z)x2+f2(z)y2]+n2χ(z)I(z,x,y),where the dimensionless tapering functions f1(z)and f2(z)can be negative or positive,depending on whether the graded-index medium acts as a focusing(χ ＞ 0)or defocusing(χ ＜ 0)linear lens.If β1= β2= β,Eq.(1)is the governing equation in[8],where spatial bright and dark similaritons with continuous wave backgrounds were studied.

This paper is organized as follows.In Sec.2,the similarity transformation for the(2+1)-dimensional NLSE is obtained,and bright and dark soliton solutions are presented.In Sec.3,the dynamics behaviors of these solitons in diあerent DDWs are analyzed.In Sec.4,a discussion concludes the paper.

2 Similarity Transformation and Soliton Solutions

According to the procedure in[3],we take the following transformation

where the amplitude A(z)and the phase ?(z,x,y)are real functions,the eあective propagation distance Z(z)and the similarity variable X(z,x,y)are both to be determined,and U(Z,X)is a complex function satisfying the traceable NLSE

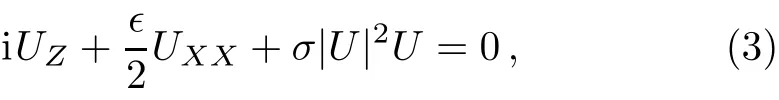
where Z=Z(z),X=X(z,x,y)and the cases with∈＞0 and∈＜0 are referred to as anomalous and normal dispersions,the subscripts mean the derivatives with respect to the corresponding variables.

Substituting the transformation(2)into Eq.(1)yields Eq.(3),but the corresponding parameters satisfy the following relations

By solving these equations self-consistently,the amplitude,phase,eあective propagation distance and similarity variable of soliton read

where the accumulated diあractionsβ2(s′)b(s′)ds′and the accumulated gain/loss Γ(z)=[γ(s)]ds.Parameters c,d,k and l are all constants.The subscript 0 denotes the initial values of the corresponding parameters at distance z=0.Parameters a and b existing in phase are related to chirped phase of solution,and they satisfy the following relation

Moreover,the parameters of system satisfy the following relation

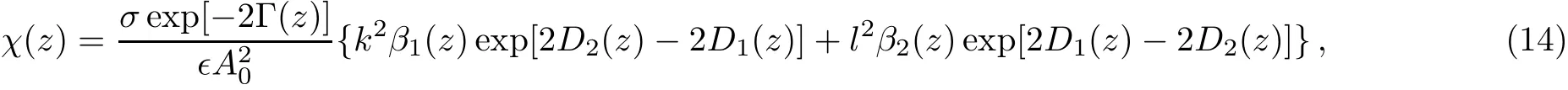
from which we know that χ(z)will be determined from parameters β1(z), β2(z),f1(z),f2(z),and γ(z).

The traceable NLSE(3)possesses rich elliptic function and diあerent soliton solutions,thus all solutions of Eq.(1)with β1= β2in[8]can be recovered by the transformation(2).Note that if the phase chirp disappears,i.e.a=0,b=0,solution(11)degenerates into a chirp-free one.Here we omit these similar solutions to Eq.(1)with β1= β2in[8],and focus on spatial bright and dark solitons as follows.

I Chirped Bright Soliton

where

II Chirped Dark Soliton

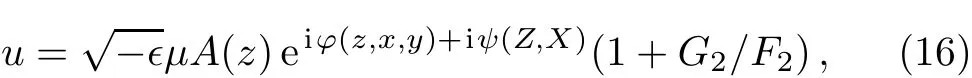
where

λj= ξj+iηjand μ =|λj|,j=1,2.

In solutions(15)and(16),A(z)and ?(z,x,y)satisfy(9)and(10),Z and X satisfy(11)and(12).

3 Dynamical Behaviors for Solitons in Diあerent DDWs

In this section,we discuss dynamical behaviors for bright and dark solitons in diあerent DDWs with the hyperbolic,Gaussian and Logarithmic prof i les.The f i rst case is the following DDW with the hyperbolic prof i le[14?15]

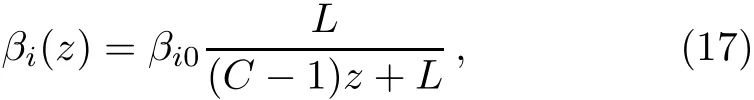
which is expressed in terms of the compression ratio parameter 1/C[value of diあraction parameters βi(z)(i=1,2)at distance z=L]and length of the waveguide L,βi0are constants related to DDW with the hyperbolic prof i le.

Fig.1 (Color online)Bright soliton pairs with separated propagation for(a)x-z plane,(b)y-z plane,and(c)and(d)x-y plane with z=5,25 respectively in DDW with the hyperbolic prof i le.The parameters are β10=b=0.2,β20=a=0.1,γ =0.01,η1= ?1.1,η2=1,ξ1= ξ2=0.8,θ10= ?0.8,θ20= ?0.7,φ10= φ20= ?0.3,A0=2,k=c=1,l=d=2,X0=0,Z0=2,∈=σ=1.

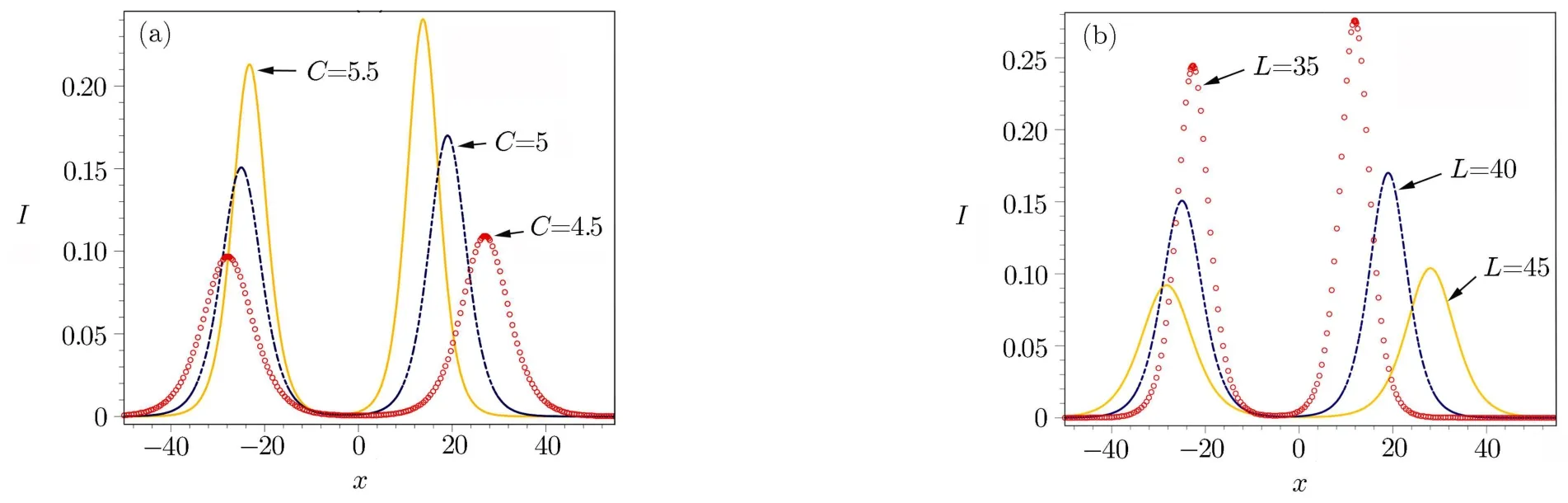
Fig.2 (Color online)Bright soliton pairs with separated propagation in the hyperbolic DDW with(a)diあerent inverse compression ratio C and(b)waveguide length L,respectively.Other parameters are chosen as the same as that in Fig.1.

In this case,the interaction scenarios pertaining to in-phase and oあ-phase injection with equal and unequal amplitudes can be dealt elaborately.Figure 1 exhibits bright soliton pairs(15)with separated propagation.Along the propagation distance z,two bright soliton gradually separate.In the same prof i le(such as hyperbolic prof i le here),for the same length L=40 in Fig.2(a),parameter C relates to the compression.The bigger the parameter C is,the more eきcient the compressed degree of soliton is.Figure 2(b)presents the degree of spreading for the same parameter C=5 in the DDW with the hyperbolic prof i le.The bigger the length of DDW is,the wider the width of soliton is.

Fig.3 (Color online)The comparison of bright solitons for x=5 in the DDWs with the hyperbolic,Gaussian and Logarithmic prof i les at distance(a)z=5 and(b)z=40,respectively.The parameters are chosen as the same as that in Fig.1.

Fig.4 (Color online)Bright soliton pairs with interaction behaviors for(a)x-z plane,(b),(c),and(d)x-y plane with z=5,8,20 respectively in DDW with the Gaussian prof i le.The parameters are η1= ?η2= ?1,ξ1= ?ξ2= ?5,θ10= ?θ20=3,φ10= φ20= ?1,and other parameters are chosen as the same as that in Fig.1.

Likewise,we examine the DDW with the Gaussian prof i le[14,16?17]

and the Logarithmic prof i le[14,16?17]

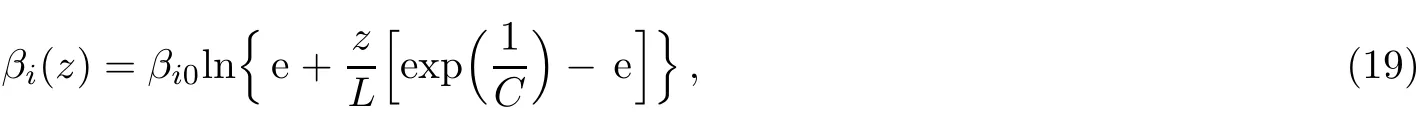
where parameters C,L and βi0have the same meaning as that in the hyperbolic prof i le,and e is the natural logarithm.

Fig.5 (Color online)Bright soliton pairs with separated propagation for(a)x-z plane and(b)y-z plane in DDW with the hyperbolic prof i le.The parameters are chosen as the same as that in Fig.4.

Fig.6 (Color online)Dark soliton pairs with separated propagation for(a)x-z plane,(b)y-z plane,and(c)and(d)x-y plane with z=5,25 respectively in DDW with the hyperbolic prof i le.The parameters are X10=2,X20=?2,δ=1,η1= ξ2=1.5,ξ1= η2=1.4,∈= ?1 and other parameters are chosen as the same as that in Fig.1.

Bright sioliton pairs with separated propagation have similar behaviors in the DDW with Gaussian and Logarithmic prof i les to that in the hyperbolic prof i le.Here we focus on the comparison of soliton properties between diあerent prof i les.From Fig.3(a),for the same parameters,the amplitude of solitons in the Logarithmic prof i le is biggest,and the amplitude in the hyperbolic prof i le is smallest,while the width of solitons has the opposite case.For the same initial shape of wave in three prof i les,after propagating through 40 length,solitons have diあerent shape and width[See Fig.3(b)].

In case of an ideal adiabatic compression or enlargement,the soliton compression or enlargement Efcan be derived as Ef=WL/W0,where W0is the full width at half maximum(FWHM)of the soliton beam at the beginning of the DDW,and WLis the FWHM of the soliton beam at the end of the DDW.Since the value of beam width is constant at the beginning of each DDW prof i les,we can compare the value of the enlargement factor at the DDW length L in each prof i le.Table 1 shows the comparison of enlargement factor over a length L=40.

Table 1 Enlargement after a length L=40.

Fig.7 (Color online)Dark soliton pairs with separated propagation in the hyperbolic DDW with(a)diあerent inverse compression ratio C and(b)waveguide length L,respectively.The comparison of dark solitons for x=5 in the DDWs with the hyperbolic,Gaussian and Logarithmic prof i les at distance(a)z=5 and(b)z=40,respectively.Other parameters are chosen as the same as that in Fig.6.

Besides bright soliton pairs with separated propagation,we can also discuss bright soliton pairs with interaction behaviors.Figure 4(a)describes Bright soliton pairs with interaction behaviors for x-z plane in DDW with the Gaussian prof i le.Two bright solitons interact and then separate.Figures 4(b)–4(d)illustrate this process of two line solitons in x-y plane.Obviously,these interaction behaviors will increase bit error rate and should be restrained.However,for the same parameters in Fig.4,bright soliton pairs with separated propagation still appear in DDW with the hyperbolic prof i le(See Fig.5).This phenomenon indicates that separating or interacting evolutional behavior of solitons in diあerent DDW needs diあerent modulating parameters.

At last,we discuss the dynamical behaviors between dark soliton pairs from solution(16).Similarly to bright soliton case,two separated dark solitons can be constructed.Figure 6 depicts dark soliton pairs with sep-arated propagation.Along the propagation distance z,two dark solitons gradually separate.In the same profi le(such as hyperbolic pro fi le here),for the same length L=40 in Fig.7(a),parameter C relates to the compression.The bigger the parameter C is,the more eきcient the compressed degree of soliton is.Figure 7(b)presents the degree of spreading for the same parameter C=5 in the DDW with the hyperbolic pro fi le.The bigger the length of DDW is,the wider the width of soliton is.

The comparison of dark solitons indicates that for the same parameters,the amplitude of solitons in the Gaussian prof i le is biggest,and the amplitude in the hyperbolic prof i le is smallest,while the width of solitons has the opposite case[See Fig.7(c)].This case is diあerent from bright soliton case in Fig.3.For the same initial shape of wave in three prof i les,after propagating through 40 length,solitons have diあerent shape and width[See Fig.7(d)].Similarly to bright soliton case,the largest enlargement of soliton still appears in the Logarithmic prof i le.

Similarly,we can discuss the interaction behaviors between two dark solitons.The related properties are similar to bright soliton case.Due to the length of limit,we omit this case.

4 Conclusions

In summary,via a universal self-similarity transformation,a systematic analysis is presented on the propagation of optical beams described by 2D variable-coeきcient NLSE with diあerent distributed transverse diあraction.The analytical 2D bright and dark soliton pairs are obtained. Based on these solutions,we mainly investigate the dynamical behaviors of solitons in three diあerent DDWs with the hyperbolic,Gaussian and Logarithmic prof i les.Results indicate that for the same parameters,the amplitude of bright solitons in the Logarithmic prof i le and the amplitude of dark solitons in the Gaussian prof i le are biggest respectively,and the amplitude in the hyperbolic prof i le is smallest,while the width of solitons has the opposite case.Moreover,soliton propagation has same properties in terms of both bright and dark solitons,that is,for the same DDW length L,the bigger the inverse compression ratio C is,the more eきcient the compressed degree of soliton is.For the same parameter C,the bigger the length of DDW is,the wider the width of soliton is.These results are potentially useful for future experiments and applications in long distance communication and all-optical ultrafast switching devices.

[1]W.P.Zhong,M.R.Beli′c,and T.W.Huang,Nonlinear Dyn.70(2012)2027.

[2]C.Y.Liu and C.Q.Dai,Commun.Theor.Phys.57(2012)568;C.Q.Dai and J.F.Zhang,Nonlinear Dyn.73(2013)2049.

[3]C.Q.Dai,Y.Y.Wang,and J.F.Zhang,Opt.Lett.35(2010)1437.

[4]Y.X.Chen and X.H.Lu,Commun.Theor.Phys.55(2011)871.

[5]H.P.Zhu,Commun.Theor.Phys.58(2012)67.

[6]Y.Y.Wang and C.Q.Dai,Commun.Theor.Phys.58(2012)255.

[7]C.Q.Dai,Y.Y.Wang,Q.Tian,and J.F.Zhang,Ann.Phys.(NY)327(2012)512;C.Q.Dai,G.Q.Zhou,and J.F.Zhang,Phys.Rev.E 85(2012)016603.

[8]C.Q.Dai,Y.Y.Wang,and J.F.Zhang,Opt.Lett.35(2010)2651.

[9]C.Q.Dai,S.Q.Zhu,L.L.Wang,and J.F.Zhang,Europhys.Lett.92(2010)24005.

[10]H.P.Zhu,Nonlinear Dyn.72(2013)873.

[11]C.Sulem and P.Sulem,The Nonlinear Schr¨odinger Equation:Self-Focusing and Wave Collapse,Springer-Verlag,Berlin(2000).

[12]I.Towers and B.A.Malomed,J.Opt.Soc.Am.B 19(2002)537.

[13]C.Q.Dai,D.S.Wang,L.L.Wang,J.F.Zhang,and W.M.Liu,Ann.Phys.(NY)326(2011)2356.

[14]M.G.Da Silva,K.Z.Nobrega,and A.S.B.Sombra,Opt.Commun.171(1999)351.

[15]M.Zitelli,B.Malomed,F.Matera,and M.Settembre,Opt.Commun.154(1998)273.

[16]R.Ganathy and V.C.Kuriakose,J.Nonlin.Opt.Phys.&Mater.11(2002)185.

[17]M.N.Vinoj and V.C.Kuriakose,J.Opt.A 6(2004)63.