N.Sepehri Javanand L.Akbari

1Department of Physics,Faculty of Sciences,University of Mohaghegh Ardabili,P.O.Box 179,Ardabil,56199-11367,Iran

2Department of Physics,Zanjan University,Zanjan,Iran

1 Introduction

Dispersion relation of a cold unmagnetized plasma for transverse electromagnetic waves is the well-known relationship:D(ω,k)= ω2? ω2p? k2c2=0,where ωp=(4πn0e2/m)1/2is the unperturbed plasma frequency(n0is the unperturbed electron density,e is the electron charge,and m is the electron rest mass).From this equation it is obvious that the cut-oあfrequency for electromagnetic radiation equals plasma frequency ωpand the propagation of waves with frequency below ωpis forbidden.It was shown by Harris[1]that in an ideal cold plasma an electromagnetic wave below the cut-oあ frequency ωs＜ ωp(Stokes wave)via the interaction with another intense electromagnetic wave ω0＞ ωp(pump wave)can propagate without absorption,if the beat-wave frequency roughly equals plasma frequency,i.e.:ω0?ωs≈ ωp.It is possible because of the modulation of plasma frequency,which determines the refractive properties of the plasma.This is due to both a relativistic increase in the electron mass and to a variation of the electron density caused by the longitudinal plasma oscillations driven by the beat-wave.In the relativistic regime of laser intensity because of the increase in the electron mass,plasma frequency decreases to ωp/γ1/2.Here γ =is the relativistic Lorentz factor of electron and a=eA/mc2is the normalized vector potential of laser amplitude.Therefore,in the relativistic regime,the dispersion relation modif i es to D(ω,k)= ω2?ω2p/γ ?k2c2=0 and consequently cut-oあfrequency of plasma decreases by the factor 1/γ.

On the analogy of process of electromagnetically induced transparency(EIT)in a neutral gas,[2?7]the term EIT was applied to describe this process.EIT in atomic systems is well-known quantum phenomenon by means of which a weak probe laser beam can propagate without experiencing any absorption.It is a technique where the complex refractive index of the probe beam(absorption and dispersion)can be changed by coupling additional coherent electromagnetic radiation.Recently,EIT in atoms has been widely investigated because of itself,and its wonderful applications to lasing without inversion[8?12]and nonlinear optics.[13?14]

After publication of the f i rst article about the application of EIT for a plasma system by Harris[1]in 1996,in the same year it was found by Matsko and Rostovtsev[15]that the excitation of the anti-Stokes wave at frequency ω0+ ωpcan aあect the conditions of EIT in cold plasma.They took into account the relativistic eあects and considered the relativistic Raman dispersion relation of Ref.[16]in the limit where the density exceeds quarter-critical.Once again it was found that an anomalous pass-band appears when the pump wave is suきciently intense.It was also found that the system exhibits Raman-type instability even when the plasma is overdense with respect to the Stokes wave.A more realistic model with considering non-uniform cold plasma was considered by Su et al.[17]The possibility of EIT in f i nite plasma was studied By Gordon et al.[18]By using a relativistic f l uid model of cold plasma,the EIT conditions for two waves of comparable,weakly relativistic amplitudes were investigated by Ersfeld and Jaroszynski.[19]

The problem of EIT for electron cyclotron waves in magnetoactive plasma was recently predicted by many authors.[20?24]Propagation of electromagnetic waves in the bounded magnetized plasma near the electron cyclotron frequency in the presence of a helical magnetic un-dulator was studied by Shvets et al.[25]They found that the both right-and left-hand circularly polarized waves can propagate along the magnetic f i eld without experiencing resonant absorption.This eあect of entirely eliminating electron cyclotron heating is referred to as the undulatorinduced transparency(UIT)of the plasma.

In most of the previous works,because of considering the low and weakly-relativistic intensities of waves,for deriving dispersion relation the terms containing waves amplitude with powers higher than the second was omitted.In this work we develop the EIT theory for high intensities of electromagnetic waves(i.e.,mildly-relativistic lasers).Based on a relativistic kinetic model,by keeping terms up to 6th powers of amplitudes,two coupled dispersion relations for two comparable intense circularly-polarized laser beams are achieved.It was shown due to the existence of the beat-wave second harmonic,the new EIT pass-band can be created in the high intensities of lasers.

2 Deriving Nonlinear Wave Equations

Let us consider two circularly-polarized electromagnetic waves with following vector potentials

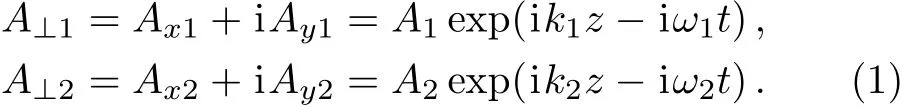
Interaction of these waves in plasma excites the longitudinal potential space-charge wave of plasma with characteristic frequencies ωLn=n(ω2? ω1),n=1,2,...We introduce the scalar potential of this wave as

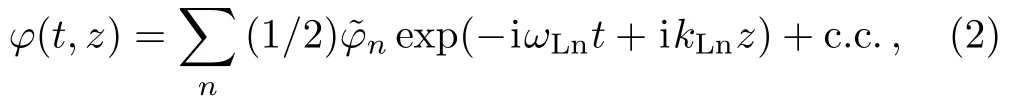
where,kLn=n(k2?k1),n=1,2,...

The full system of equations,which describes the nonlinear interaction of electromagnetic waves in the plasma,is[26]

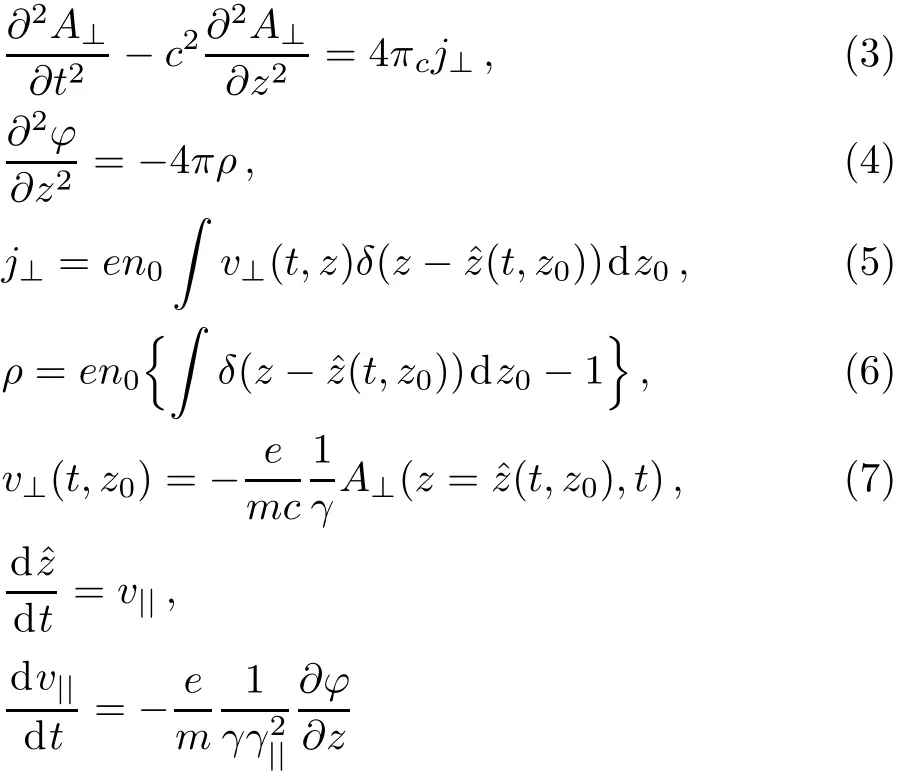
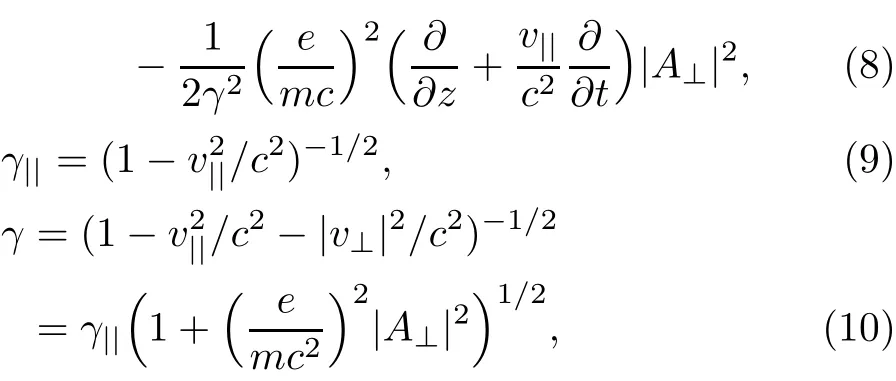
where,A⊥=A⊥1+A⊥2is the total vector potential of electromagnetic waves,v⊥(z0,t)=vx(z0,t)+ivy(z0,t)is the complex transverse velocity of electron which depends on the initial coordinate z0,v||(t,z0)is the longitudinal velocity of electrons,?z(t,z0)is the position of one electron which has been located at z0in the initial time and n0is the unperturbed initial density of plasma.

We insert A⊥from Eq.(2)into Eq.(3),then multiply the resulting equation by exp(iω1t?ik1z)(exp(iω2t?ik2z))and integrate it with respect to z in the interval[0,λL),where λL=2π/kL1is the wavelength of the f i rst harmonic of electron Langmuir wave.In this way,we can obtain the following equations

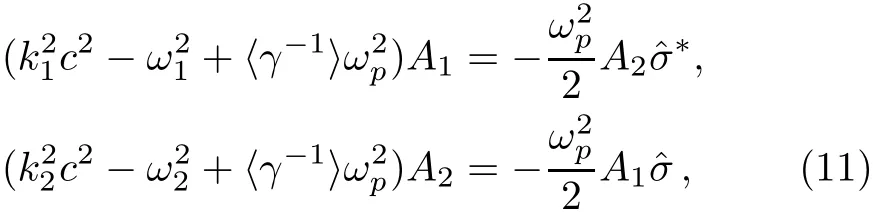
where,we use the following def i nitions

Now,by substituting ? from Eq.(2)into the Poisson’s equation(4),multiplying the resulting equation by exp(iωLnt? ikLnz)and doing the same averaging procedure we can f i nd

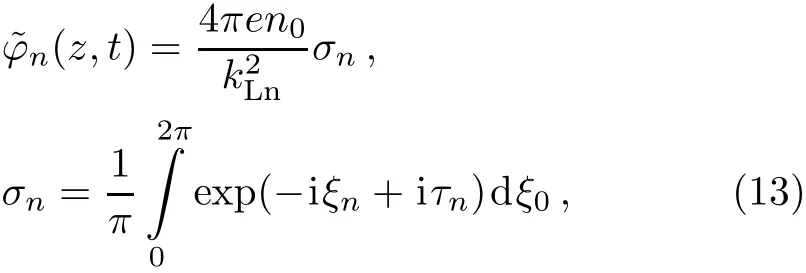
where,we have the next def i nitions

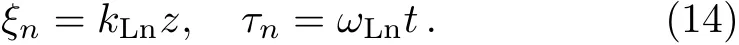
Substituting ?(with considering relation given by Eq.(13))and A⊥into the equation of electrons motion(8)leads to the following

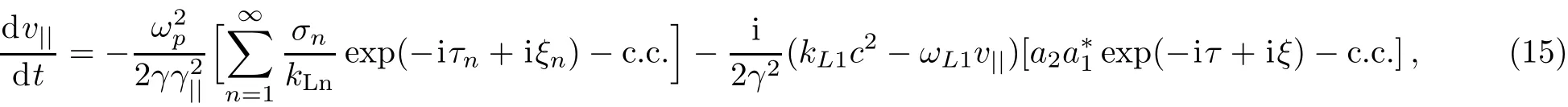
where,a1=(e/mc2)A1and a2=(e/mc2)A2are the dimensionless vector potentials and

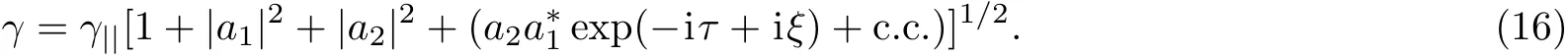
3 Dispersion Relations

We shall begin to investigate the system of equations in the linear approximation,assuming for the unperturbed state(when a1,2=0)plasma is cold and we have:γ||(t=0)=γ(t=0)=1.In the linear respect to?z and v||approximation,with considering small perturbations of?v and?z we assume

In this approximation we can write the following

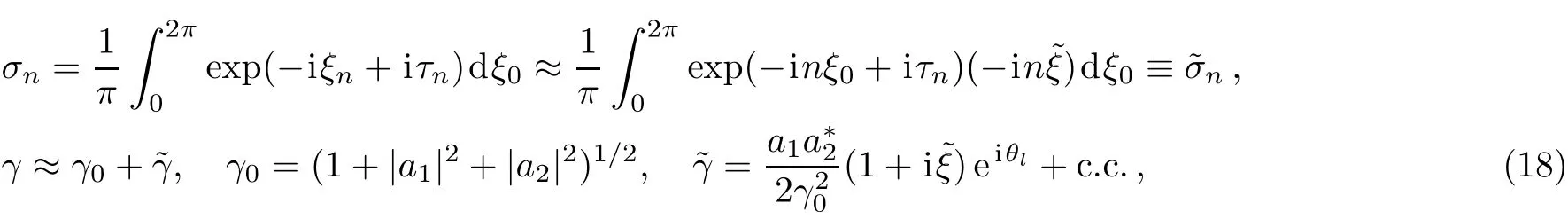
where,θl=?τ+ξ0.For obtaining Eq.(18)we have assumed that for f i nite n the inequality|n?ξ|?1 is satisf i ed and we can write:exp(±in?ξ)≈1±in?ξ.

Now in the def i nition of?σ(second expression of Eq.(12)),we can expand γ?1in powers of the vector potentials.In this expansion by saving up to the 6thorder of vector potentials power,we get

It should be better to notice that the minimum power of amplitudes in?σnequals 2n(i.e.|?σn|∝|a1a2|n+h.o.(a1a2))therefore the last term of Eq.(19)that contains?σ3vanishes and only we need to f i nd?σ1and?σ2.For calculating?σ1and?σ2we return to the motion equation(15).In the linear approximation this equation can be written as

For obtaining Eq.(20)we assumed kL1c2?ωL1?v that means the longitudinal oscillation of electrons is nonrelativistic.By multiplying Eq.(20)to the operator

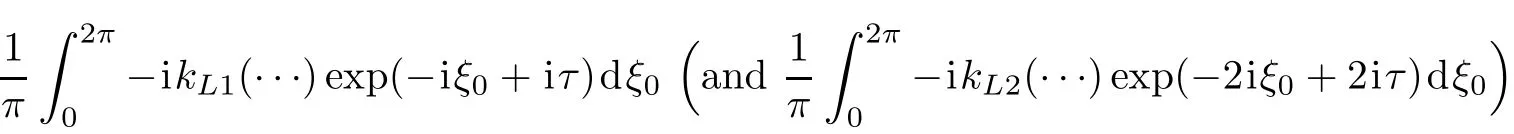
we can derive

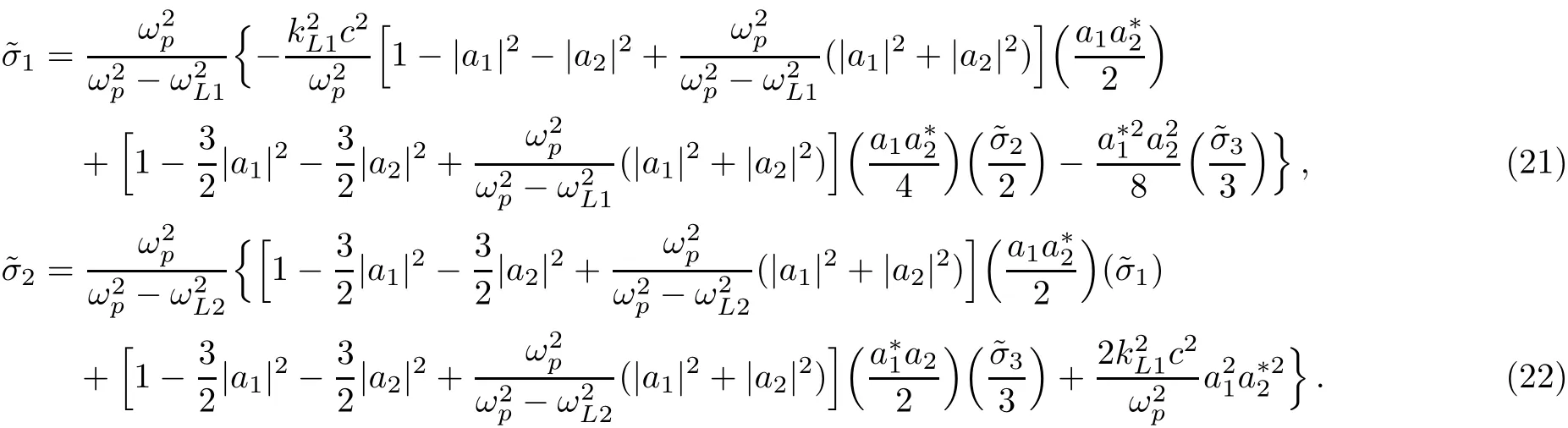
In the above equations since the terms containing?σ3have the orders higher than 6thhence we can neglect them.In this case after solving these algebraic equations we can obtain

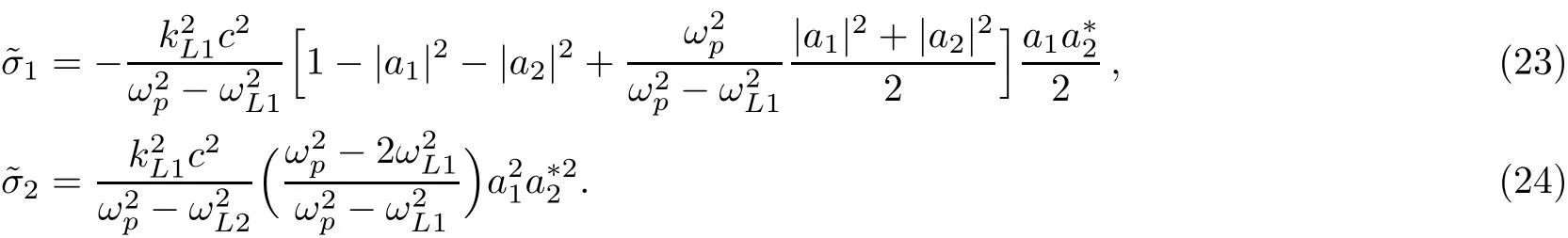
Now by inserting?σ1and?σ2into Eq.(19)and neglecting the terms higher than 6thorder of amplitudes we can achieve

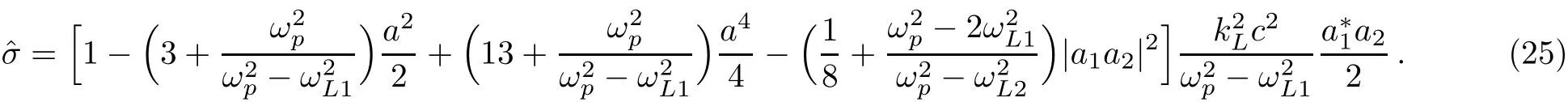
In Eq.(25),we have assumed a2=|a1|2+|a2|2,for simplicity.In the linear approximation,by expanding γ?1in the fi rst equation of(12),we can derive

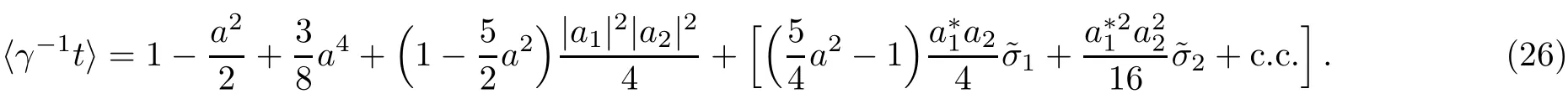
Substituting Eqs.(25)and(26)into Eqs.(11)and neglecting expressions including lasers amplitude powers higher than 6th,leads to the following coupled dispersion relations:

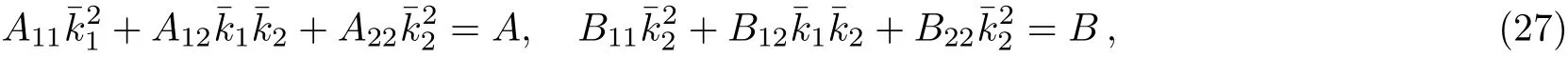
where,

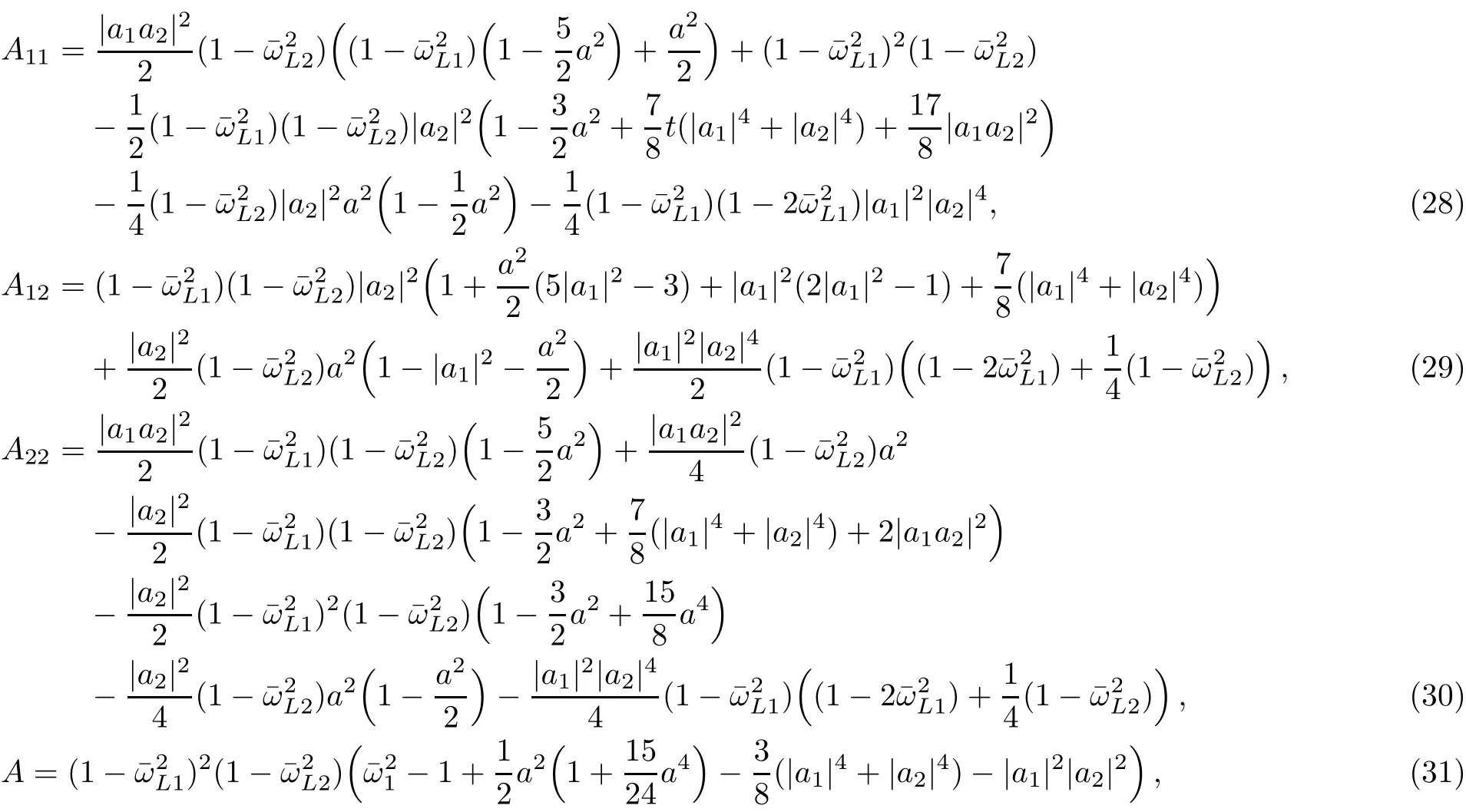
where,we use dimensionless variablesˉωα=ωα/ωp,ˉkα=kαc/ωp,α =1,2,L1,L2.Coeきcients B11,B12,B22,and B can be obtained from A11,A12,A22,and A,respectively,by interchanging(ω1,k1,a1)? (ω2,k2,a2).

Neglecting high orders of amplitudes and maintaining only the second orders in Eqs.(27)leads to the same analytical results of Ref.[8]for circularly polarized waves.

4 Numerical Results

A numerical study has been performed for simultaneous solving of dispersion equations(27).If for real frequenciesˉω1andˉω2the wave numbersˉk1andˉk2are both real,both of the waves can propagate through plasma without absorption and plasma is transparent.For a f i xedˉω1the real values ofˉω2,ˉk1,andˉk2that simultaneously satisfy Eqs.(27)have been obtained through an iterative method.

In Fig.1 for|a1|=|a2|=0.2 andˉω1=1.2 variation ofˉk1andˉk2with respect toˉω2is demonstrated.EIT occurs in the region whereˉω2?ˉω1≈1.The thick curves denoteˉk2(ˉω2)while the thin curves denoteˉk1(ˉω2).There are two branches in the left and right sides of the pointˉω2=ˉω1?1=0.2 that approach to inf i nity in this point.The width of pass-band that plasma is transparent for both waves equals δˉω≈0.06.Except the asymptotic regions,the variation ofˉk1(ˉω2)is negligible.In Fig.2 the value of f i rst wave frequency increases toˉω1=1.6.We can see that the width of pass-band increases to δˉω≈0.09.In Fig.3(b)forˉω1=1.8 the right-hand region of dispersion curves were mixed with the ordinary dispersion curves.For more visibility we have separately plotted the lefthand region of dispersion in Fig.3(a).

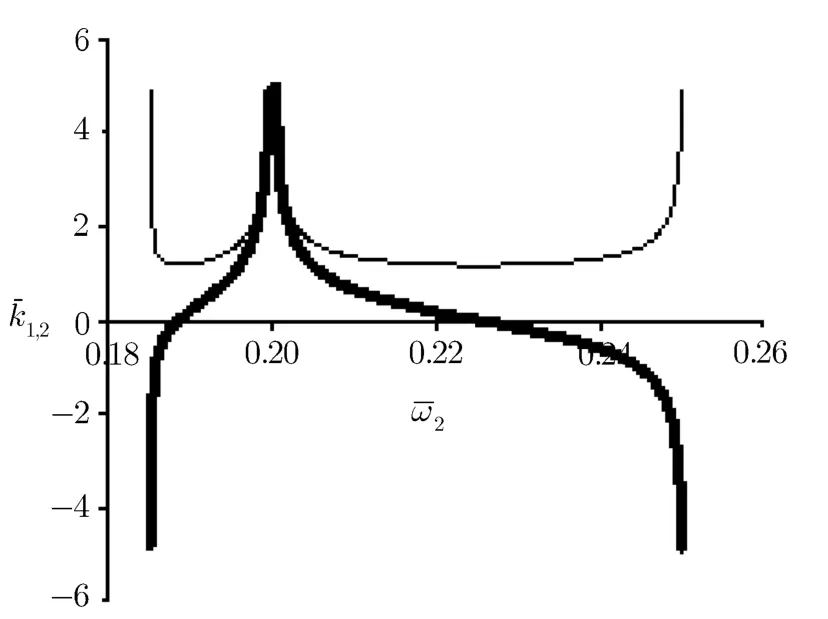
Fig.1Dispersion curves ofˉk1(ˉω2)(thin curves)andˉk2(ˉω2)(thick curves)for f i xedˉω1=1.2 and|a1|=|a2|=0.2.

In Figs.4(a)and 4(b)we have represented dispersion curves for|a1|=|a2|=0.4 andˉω1=1.2.We see that besides the f i rst area around the pointˉω2?ˉω1≈1,other region appears correspond to the second harmonic of beatwave resonance 2(ˉω2?ˉω1)≈1.The width of pass-band is very narrow δˉω≈0.0012.For low intensities of lasers this region vanishes.Figures 5(a)and 5(b)show the dispersion curves for|a1|=|a2|=0.4 andˉω1=1.4.In this case the region created by the second harmonic resonance is mixed with the ordinary dispersion curves.The pass-band width of f i rst harmonic is δˉω≈0.28.

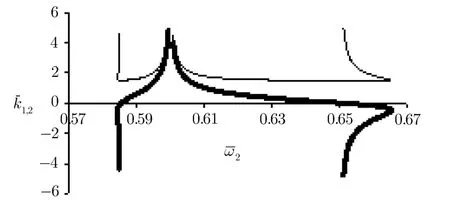
Fig.2Dispersion curves ofˉk1(ˉω2)(thin curves)andˉk2(ˉω2)(thick curves)for f i xedˉω1=1.6 and|a1|=|a2|=0.2.

Fig.3Dispersion curves ofˉk1(ˉω2)(thin curves)andˉk2(ˉω2)(thick curves)for f i xedˉω1=1.8 and|a1|=|a2|=0.2.

Figures 6(a)and 6(b)shows the dispersion curves for diあerent intensities of lasers powers|a1|=0.4,|a2|=0.2,andˉω1=1.2.For the f i rst region the pass-band width is δˉω≈0.16 and for the second region this width becomes very narrow δˉω≈0.000 16.It is clear that eあect of second harmonic is considerable only for high intensities.

In Figs.7 and 8 we set the intensity of f i rst laser very greater than the second|a1|=0.4,|a2|=0.01.This case corresponds to the works of Harris,[1]Matsko,and Rostovtsev.[15]The f i rst intense laser with frequency greater than the plasma frequency called “pump” and the second weak laser with frequency below the plasma frequency called “probe”. In Fig.7 we have selectedˉω1=1.2.The pass-band width is δˉω≈0.12.It is clear that in this case the value of pump wave numberˉk1is nearly constant.The weak probe can not eあect on the pump and the dispersion of the pump wave remains unchanged as:D1(ˉω1,ˉk1)=ˉω21?ˉk21?(1?|a1|2/2)=0.Increasing the pump frequency toˉω1=1.8 in Fig.8 causes the composition of EIT branches of dispersion with ordinary branches.

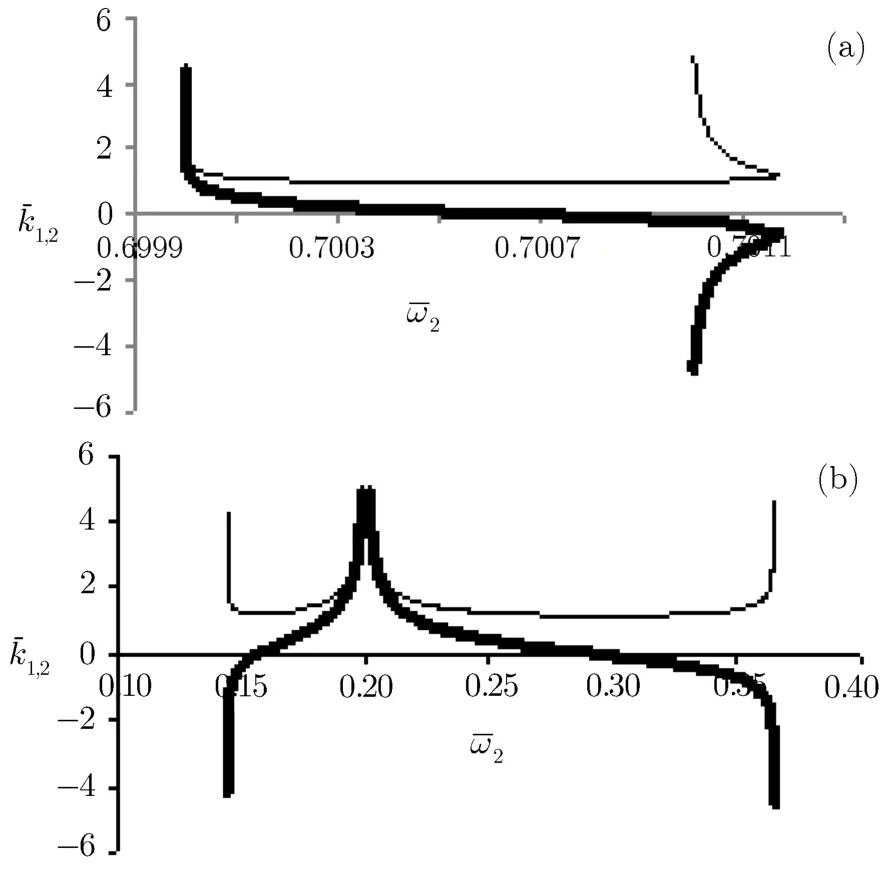
Fig.4Dispersion curves ofˉk1(ˉω2)(thin curves)andˉk2(ˉω2)(thick curves)for f i xedˉω1=1.2 and|a1|=|a2|=0.4.

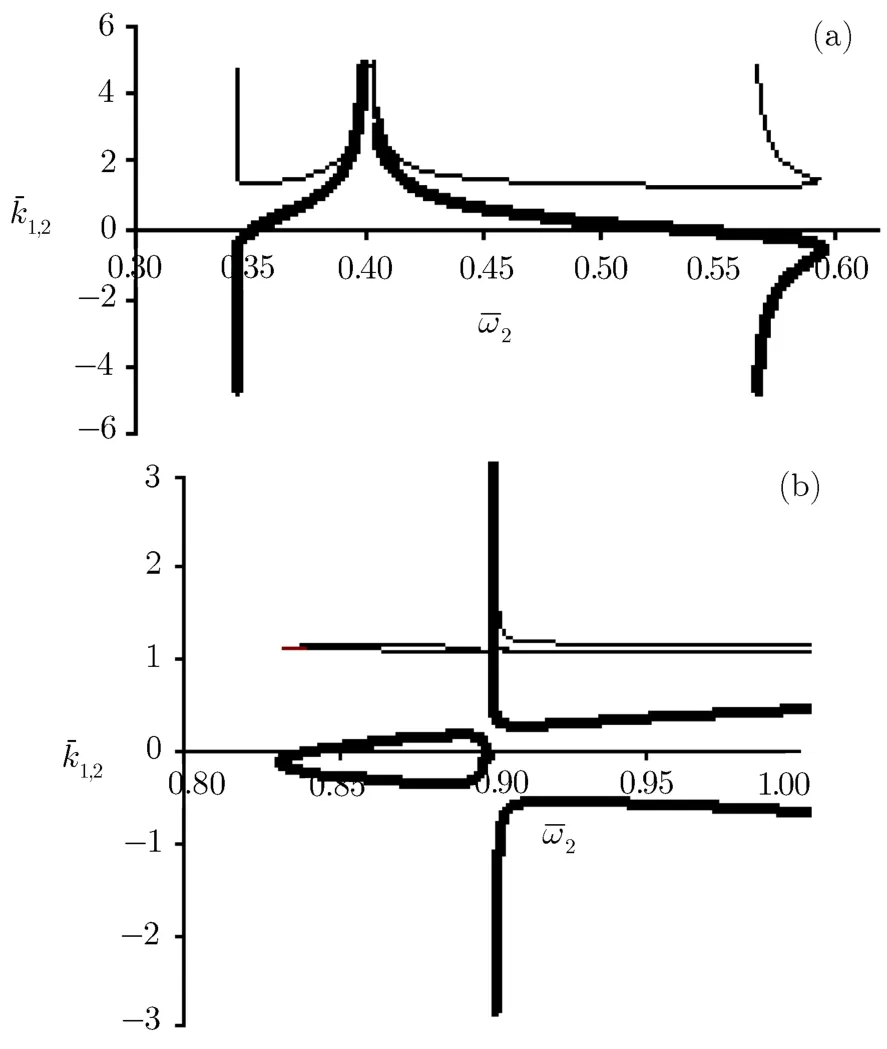
Fig.5Dispersion curves of(ωˉ2)(thin curves)and(ωˉ2)(thick curves)for fi xedωˉ1=1.4 and|a1|=|a2|=0.4.

5 Experimental Setup

To realize the results of the paper,we propose a schematic experimental set-up.Schematic diagram of the suggested experiment is shown in Fig.9.Two microwave laser beams(pump and probe waves)coincide together by an optical system and inject into the plasma chamber.The frequency of probe wave can be controlled by a microwave oscillator.A Langmuir probe is employed for detection of plasma density and evaluation of plasma frequency.The plasma emitter which consists of thermionic and thermoelectronic materials produces the plasma source.A horn antenna is placed on the other side of the plasma chamber to detect the transmitted probe wave.Variation of the probe frequency should detect the EIT for two diあerent transparent frequency bands,as mentioned earlier.It should be better to mention that such a system is used by Ref.[27]to investigate the EIT of magnetized plasma,experimentally.

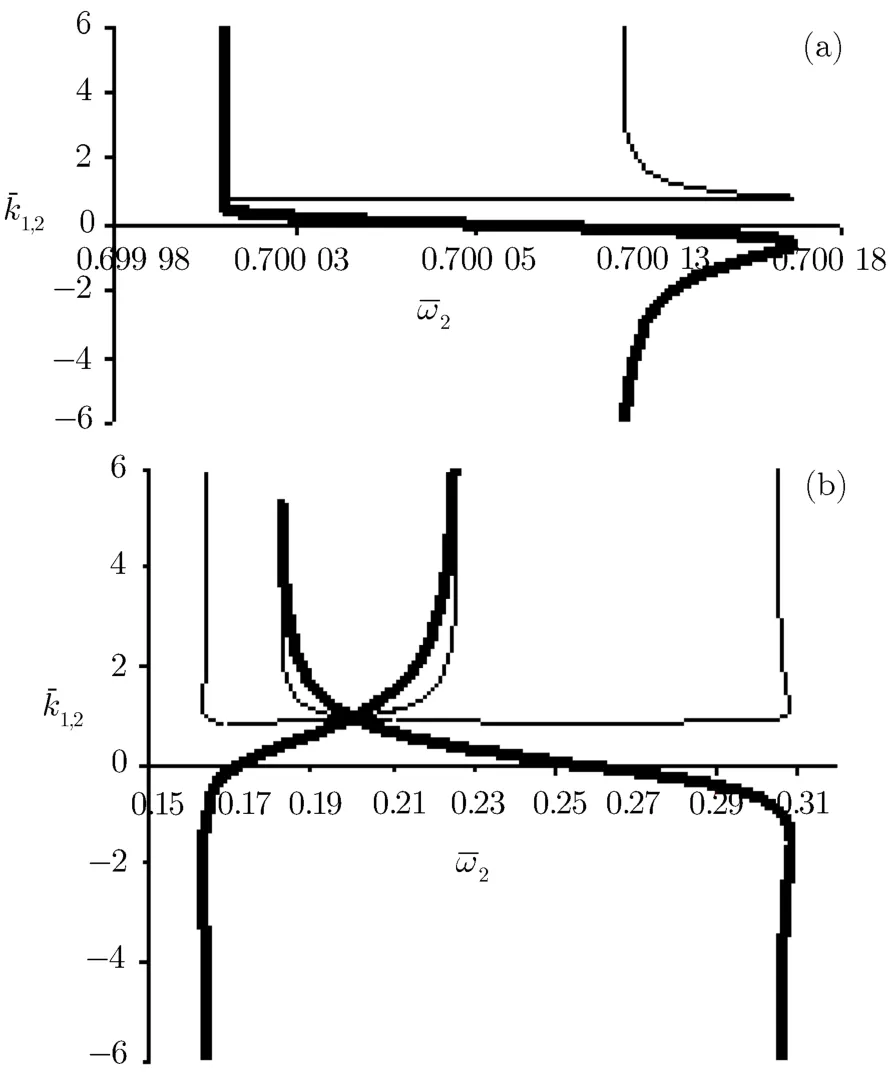
Fig.6Dispersion curves ofˉk1(ˉω2)(thin curves)andˉk2(ˉω2)(thick curves)for f i xedˉω1=1.2 and|a1|=0.4,|a2|=0.2.

6 Conclusions

In this paper we have studied the problem of EIT for two mildly-relativistic lasers.Maintaining the high orders of amplitudes leads to the creation of new pass-band region.This is because of the resonance in the second harmonic of plasma beat-wave.This region is considerable only for high intensities of lasers.In f i xed values of amplitudes,increase in the f i rst laser frequency causes increase in the width of EIT pass-band.Also,for a f i xed frequency of the f i rst wave increase in the amplitude of each electromagnetic wave leads to the increase in the pass-band width.

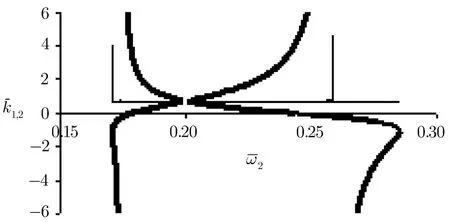
Fig.7Dispersion curves ofˉk1(ˉω2)(thin curves)andˉk2(ˉω2)(thick curves)for f i xedˉω1=1.2 and|a1|=0.4,|a2|=0.01.

Fig.8Dispersion curves ofˉk1(ˉω2)(thin curves)andˉk2(ˉω2)(thick curves)for f i xedˉω1=1.8 and|a1|=0.4,|a2|=0.01.

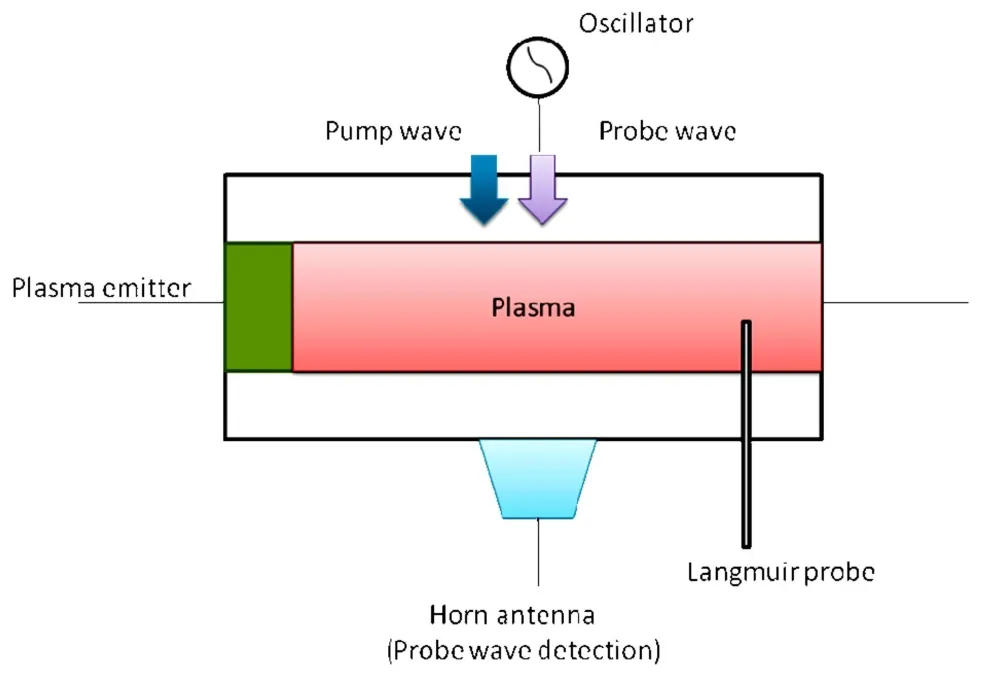
Fig.9 Schematic diagram of proposed experimental setup.

[1]S.E.Harris,Phys.Rev.Lett.77(1996)5357.

[2]K.J.Boller,A.Imamoglu,and S.E.Harris,Phys.Rev.Lett.66(1991)2593.

[3]J.E.Field,K.H.Hahn,and S.E.Harris,Phys.Rev.Lett.67(1991)3062.

[4]M.Xiao,Y.Li,S.Jin,and J.G.Banacloche,Phys.Rev.Lett.74(1995)666.

[5]J.G.Banacloche,Y.Li,S.Jin,and M.Xiao,Phys.Rev.A 51(1995)576.

[6]D.J.Fulton,S.Shepherd,R.R.Moseley,B.D.Sinclair,and M.H.Dunn,Phys.Rev.A 52(1995)2302.

[7]F.S.Catalliotti,C.Ffort,T.W.Hansch,M.Inguscio,and M.Prevedelli,Phys.Rev.A 56(1997)2221.

[8]A.Imamoglu,J.E.Field,and S.E.Harris,Phys.Rev.Lett.66(1991)1154.

[9]G.S.Agarwal,Phys.Rev.A 44(1991)R28.

[10]J.Y.Gao,et al.,Opt.Commun.93(1992)323.

[11]J.Y.Gao,et al.,Opt.Commun.110(1994)590.

[12]G.G.Padmabandu,et al.,Phys.Rev.Lett.76(1996)2053.

[13]K.Halita,L.Marmet,and B.P.Stoicheあ,Phys.Rev.A 45(1992)5152.

[14]L.V.Hau,S.E.Harris,Z.Dutton,and C.H.Behroozi,Nature(London)397(1999)594.

[15]A.B.Matsko and Y.V.Rostovtsev,Phys.Rev.E 58(1996)7846.

[16]C.J.McKinstrie and R.Bingham,Phys.Fluids B 1(1989)230.

[17]X.M.Su,P.Dong,J.Y.Gao,and K.Muraoka,Eur.Phys.J.D 12(2000)193.

[18]D.F.Gordon,W.B.Mori,and C.Joshi,Phys.Plasmas 7(2000)3145.

[19]B.Ersfeld and D.A.Jaroszynski,J.Mod.Optics 49(2002)889.

[20]A.Yu.Kryachko,A.G.Litvak,and M.D.Tokman,J.Exp.Theor.Phys.95(2002)697.

[21]A.G.Litvak and M.D.Tokman,Phys.Rev.Lett.88(2002)095003.

[22]G.Shvet and J.S.Wurtele,Phys.Rev.Lett.89(2002)115003.

[23]G.Shvet and M.Tushentsov,J.Mod.Optics 50(2003)2583.

[24]M.S.Hur,J.S.Wurtele,and G.Shvets,Phys.Plasmas 10(2003)3004.

[25]M.Shvets,M.Tushentsov,M.D.Tokman,and A.Kryachko,Phys.Plasmas 12(2005)056701.

[26]M.V.Kuzelev and A.A.Rukhadze,Plasma Free Electron Lasers,Editions Frontieres,France(1995).

[27]E.Kawamori,T.Y.Hsieh,Y.Nishida,and C.Z.Cheng,Plasma Phys.Control.Fusion 54(2012)124022.