HE Guan-Sheng(賀觀圣)and LIN Wen-Bin(林文斌)

School of Physical Science and Technology,Southwest Jiaotong University,Chengdu 610031,China

1 Introduction

The gravitational f i eld of moving source and the related dynamics of particle or photon are of great interest to the relativity community.[1?5]Aichelburg and Sexl derived the metric and investigated the gravitational f i eld for a massless point particle moving with the velocity of light,via the combination of the isotropic Schwarzschild metric and a singular Lorentz transformation.[6]Kopeikin and Sch¨afer developed the Lorentz covariant theory of propagation of light in the weak gravitational f i elds of N point masses with arbitrary velocities,in which the authors derived the explicit formulation of light def l ection in term of the retarded time and investigated the light propagation for moving gravitational lenses in detail.[7]With the combination of a nearly Lorentz transformation and the isotropic Schwarzschild metric,Adler obtained the parameterized metric of a point mass for the motion in any direction.[8]Wucknitz and Sperhake presented the“2+1”D space-time metric of the gravitational lens with an arbitrary velocity in the weak-f i eld limit,and investigated the eあects of the lens’high velocity on the dynamics of the particle and photon in detail.[9]

In this paper we present the exact metric of a uniformly moving Schwarzschild black hole in the harmonic coordinates. Note the metric outside the horizon of Schwarzschild black hole is same as that of point mass,we do not discriminate them through this paper.As an application,we derive explicit formulations for the dynamics of photon and particle in the weak-f i eld limit of the gravitational source whose velocity is close to the speed of light.

This paper is organized as follows.Section 2 presents the derivation of the harmonic metric of a uniformly moving point mass.Section 3 calculates the dynamics of photon and particle in the weak fi eld.Conclusion is given in Sec.4.We use unit with c=1 throughout.Since the gravitational fi eld of the static point mass can be described by Schwarzschild metric,we do not distinguish the metric(or fi eld)of the point mass from that of Schwarzschild black hole.

2 Metric for Uniformly Moving Point Mass in Harmonic Coordinates

The energy-momentum tensor of a static point mass m located at the coordinate origin(0,0,0)can be written as

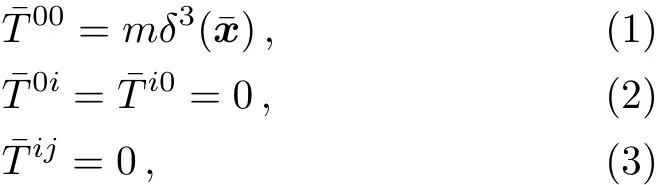
whereˉx≡(ˉx1,ˉx2,ˉx3),and δ3is 3D Dirac delta function.i,j=1,2,3.

The gravitational f i eld for the point mass is described by Schwarzschild metric,the harmonic form of which can be written as[10]

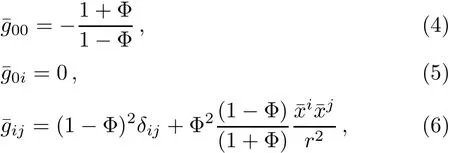
where δijdenotes Kronecker delta.G is gravitational constant,Φ=?Gm/r is Newtonian potential,and r2=ˉx2.

The energy-momentum tensor of a uniformly moving point mass can be obtained from the energy-momentum tensor of the static point mass via Lorentz transformation with

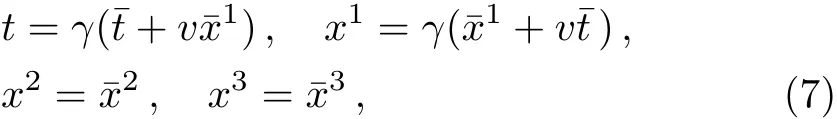
here we assume the velocity vector v of the point mass is along the positive x1-axis without loss of generality,and γ =(1?v2)?1/2is Lorentz factor.We have

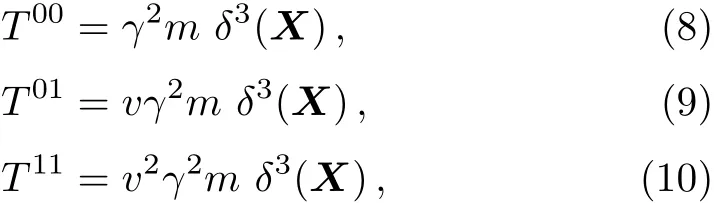
where X ≡ (X1,X2,X3)≡ (γx1? γvt,x2,x3).

The multipole expansion of the energy-momentum tensor of a uniformly moving point mass can be written as

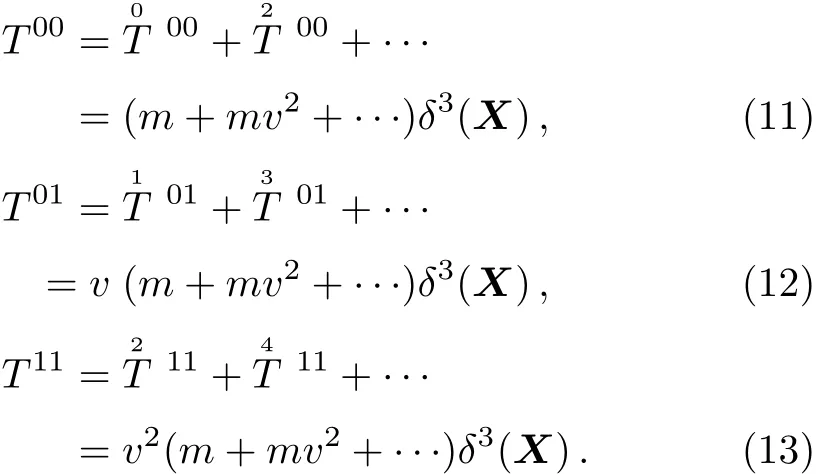
The multipole expansion of the uniformly moving point mass and momentum can be calculated as follows[10]

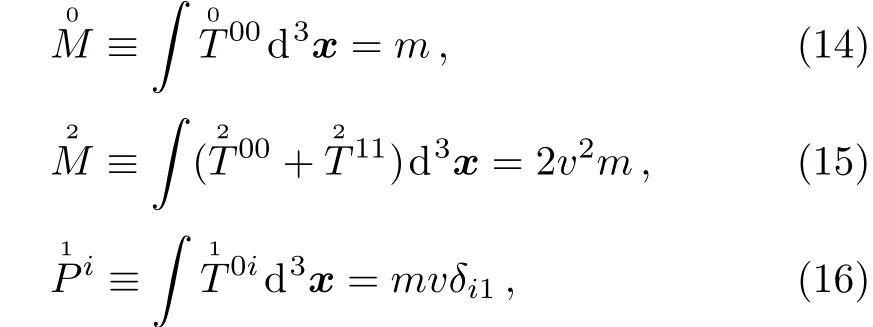
where x=(x1,x2,x3),and the multipole f i elds for the uniformly moving point mass can be written as

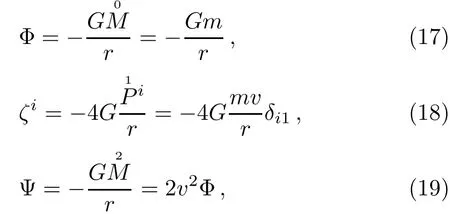
where ζ is a new vector potential,and Ψ is called as the second potential.The metric tensor based on these multipole f i elds,which is also regarded as the post-Newtonian approximation,can be written as[10]

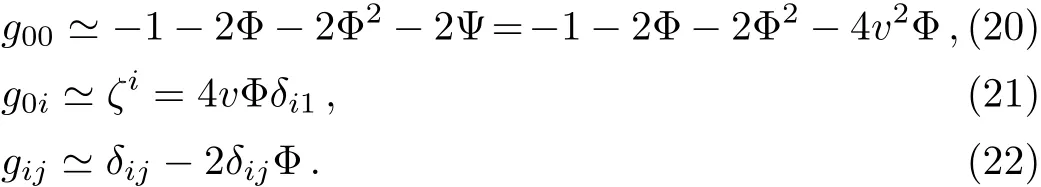
The above multipole f i elds or the corresponding metric tensor can only describe the far f i eld for the slowly moving gravitational source.Therefore,we need a more accurate metric tensor to describe the gravitational f i eld in the near region of one moving black hole,or in both the near and far regions of the gravitational source with a relativistic velocity.In this paper the near region is def i ned as the one in which Φ～1.

Einstein’s equation is generally covariant,therefore,the metric of the uniformly moving point mass can be obtained via applying the Lorentz transformation Eq.(7)to the harmonic Schwarzschild metric Eqs.(4)–(6).After performing straightforward but tedious calculations,we fi nally obtain

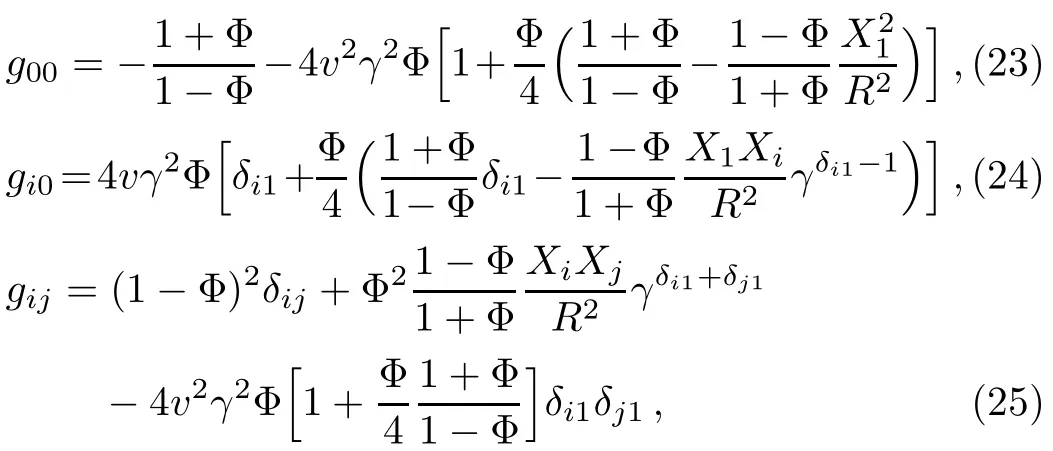
Since the harmonic coordinate condition is Lorentz covariant and Eqs.(4)–(6)are exact,Eqs.(23)–(25)are the exact harmonic metric for the uniformly moving point mass or Schwarzschild black hole with an arbitrary velocity.To our knowledge,this formulation has not been reported before.

It can be seen that this harmonic metric reduce to the harmonic Schwarzschild metric if one sets v=0,and from these equations we can also recover the multipole fi elds of the moving point mass(see Eqs.(20)–(22))when v2～Φ?1.

3 Dynamics of Particle and Photon in Weak-Field Limit

As an application,we consider the dynamics of photon and particle in the far region with Φ ? min{1,1/vγ2}.In this region,the metric Eqs.(23)–(25)can be approximated as follows:

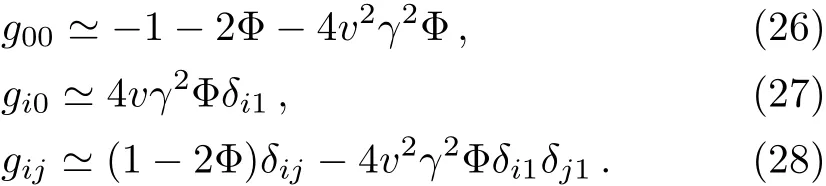
It can be seen that Eqs.(26)–(28)are consistent with the“2+1”D metric given by Wucknitz and Sperhake.[9]

The dynamics of photon and particle can be obtained via the geodesic equation.Let u=dx/dt denote the contravariant velocity vector of photon.After performing tedious but straightforward calculations of the Christoあel symbols,we have

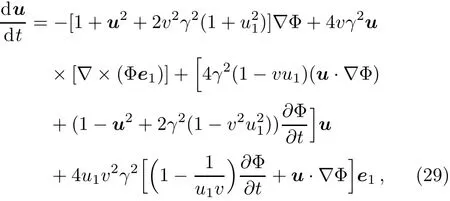
where

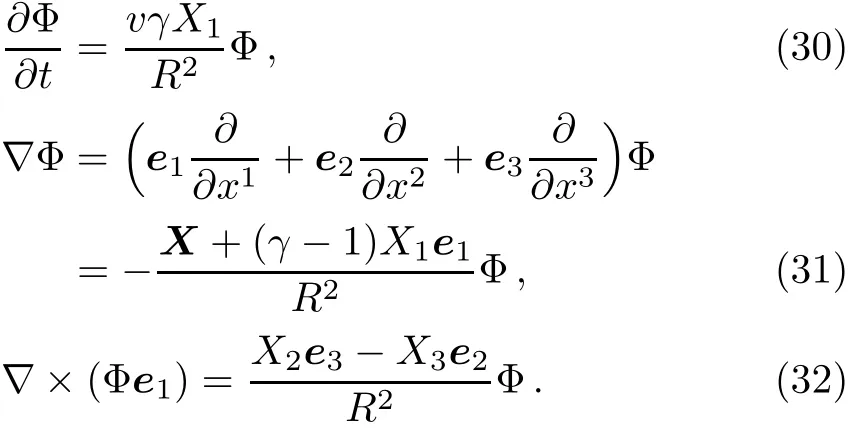
Here eidenotes the unit vector of xi-axis,and u1denotes the x1-axis component of the contravariant velocity vector u for the convenience of display.Equation(29)is also valid for the particle dynamics.Let w denote the particle velocity,whose amplitude is usually very small.For w2～Φ?1,the particle dynamics can be written as Notice that X1,X,R,and Φ are functions of t.This equation shows that the test particle undergoes an additional retarded centripetal force due to the relativistic motion of source,since 2v2γ2is always positive.

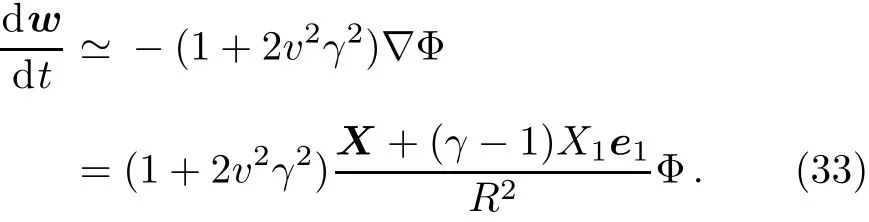
On the other hand,it can also be drawn from Eqs.(29)and(33)that the force induced by the source motion may be comparable to or even larger than the conventional Newtonian gravitational force when the velocity of source is high enough.

4 Conclusion

Basing on the general covariance of Einstein’s equation,we apply Lorentz transformation to the harmonic form of Schwarzschild metric,and obtain the metric for the uniformly moving Schwarzschild black hole in the harmonic coordinates.To our knowledge,this harmonic metric has not been reported before.When the velocity of gravitational source is low,the harmonic metric reduces to the post-Newtonian approximation for the moving point mass in the weak-f i eld limit.As an application,we derive the dynamics of photon and particle in the far f i eld of the moving Schwarzschild black hole with an arbitrary velocity.It is found that the relativistic motion of source can introduce an additional retarded centripetal force on the test particle,which may be comparable to or even larger than Newtonian gravitational force.The harmonic metric obtained in this work might also be helpful in studying the dynamics of particle or photon in the strong f i eld dominated by one fast moving massive black hole.

[1]T.Pyne and M.Birkinshaw,Astrophys.J.415(1993)459.

[2]S.Kopeikin and B.Mashhoon,Phys.Rev.D 65(2002)064025.

[3]S.Molnar and M.Birkinshaw,Astrophys.J.586(2003)731.

[4]S.M.Kopeikin and V.V.Makarov,Phys.Rev.D 75(2007)062002.

[5]S.M.Kopeikin,Mon.Not.R.Astron.Soc.399(2009)1539.

[6]P.C.Aichelburg and R.U.Sexl,Gen.Rel.Grav.2(1971)303.

[7]S.M.Kopeikin and G.Sch¨afer,Phys.Rev.D 60(1999)124002.

[8]R.J.Adler,Gen.Rel.Grav.31(1999)1837.

[9]O.Wucknitz and U.Sperhake,Phys.Rev.D 69(2004)063001.

[10]S.Weinberg,Gravitation and Cosmology:Principles and Applications of the General Theory of Relativity,Wiley,New York(1972)p.184;p.257-260.