B.I.Ita,A.I.Ikeuba,and A.N.Ikot

1Theoretical Quantum Chemistry Group,Department of Chemistry,University of Calabar,Nigeria

2Theoretical Physics Group,Department of Physics,University of Uyo,Nigeria

1 Introduction

The bound state solutions of the Schr¨odinger equation(SE)are only possible for some potentials of physical interest.[1?5]These solutions could be exact or approximate and they normally contain all the necessary information for the quantum system.Quite recently,several authors have tried to solve the problem of obtaining exact or approximate solutions of the Schr¨odinger equation for a number of special potentials.[6?10]Some of these potentials are well-known to play very important roles in many fi elds of Physics such as Molecular Physics,Solid Sate,and Chemical Physics.[8]

The purpose of the present work is to present the solution of the Schr¨odinger equation with the quantum mechanical gravitational potential(QMGP)plus the harmonic oscillator potential(HOP)of the form:

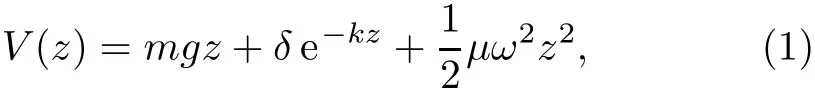
where z is the displacement,k is momentum,m is the mass,g is gravitational acceleration,δ is an adjustable parameter,μ is the reduced mass,and ω is the angular frequency.The QMGP could be used to calculate the energy of a body falling under gravity from quantum mechanical point of view.Berberan–Santos et al.[11]have studied the motion of a particle in a gravitational f i eld using the QMGP without the exponential term.They obtained the classical and quantum mechanical position probability distribution function for the particle.Also,quite recently,Ita and Ikeuba[12]solved the Klein–Gordon equation with QMGP.However,not much has been achieved in the area of solving the Schr¨odinger equation with the QMGP in the literature.The HOP has been widely studied in the literature.For example,Amore and Fernandez[13]studied the two-particle harmonic oscillator in a one-dimensional box and obtained energy eigen values which were comparable with energies from variational and perturbation methods.Jasim et al.[14]also investigated the single particle level density in a harmonic oscillator potential well and obtained very interest results.They studied the properties of the partial level density and the total level density numerically for the harmonic oscillator potential well.Also,Ikot et al.[15]derived the energy eigen values and the corresponding eigen functions for the two-dimensional harmonic oscillator potential in Cartesian and polar coordinates using the NIkiforov–Uvarov method.Wang et al.[16]determined the Virial theorem for a class of quantum nonlinear harmonic oscillators.

2 Nikiforov–Uvarov(NU)Method

The NU method is based on the solutions of a generalized second order linear diあerential equation with special orthogonal function.[17]The Schr¨odinger equation of the type as:

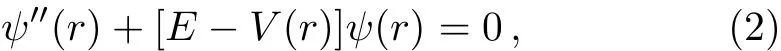
could be solved by this method.This can be done by transforming Eq.(2)into an equation of hypergeometrictype with appropriate coordinate transformation s=s(r)to get

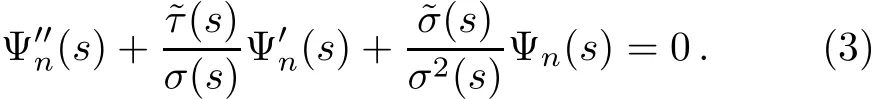
To solve Eq.(3)we can use the parametric NU method.[18]The parametric generalization of the NU method is expresses by the generalized hypergeometric-typeequation[6]

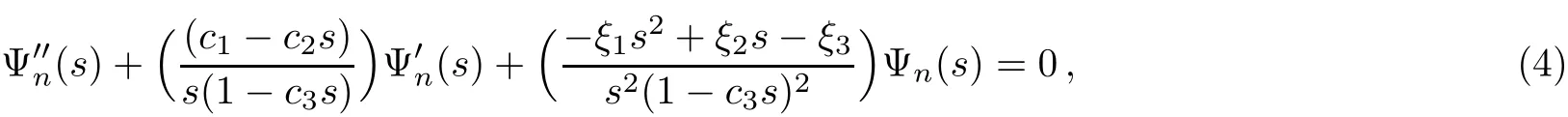
where σ(s)and?σ(s)are polynomials at most second degree and?τ(s)is a f i rst degree polynomial.The eigen functions and the corresponding eigen values to the equation become

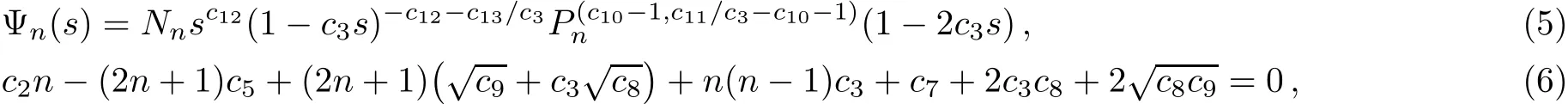
where

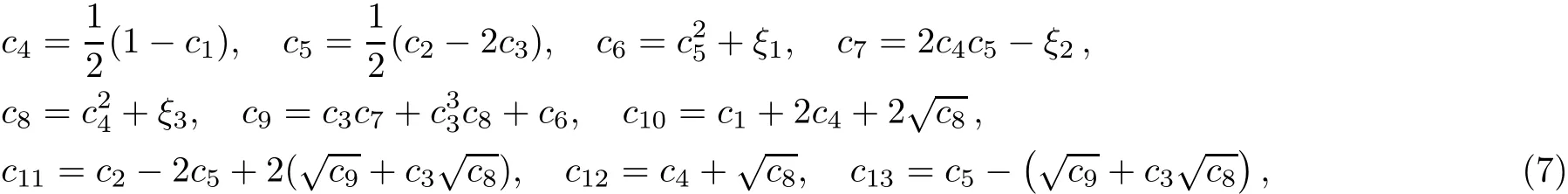
where Nnis a normalization constant and P(α,β)n(x)are the Jacobi polynomials.

3 The Schr¨odinger Equation

In spherical coordinate Schr¨odinger equation with the potential V(r)is given as[6]

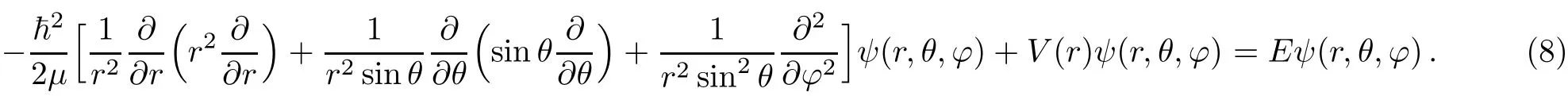
Using the common ansatz for the wave function:

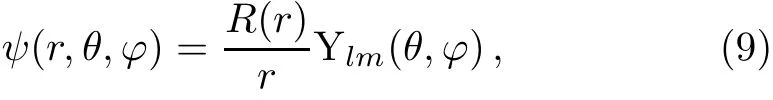
into Eq.(8),we get the following set of equations:

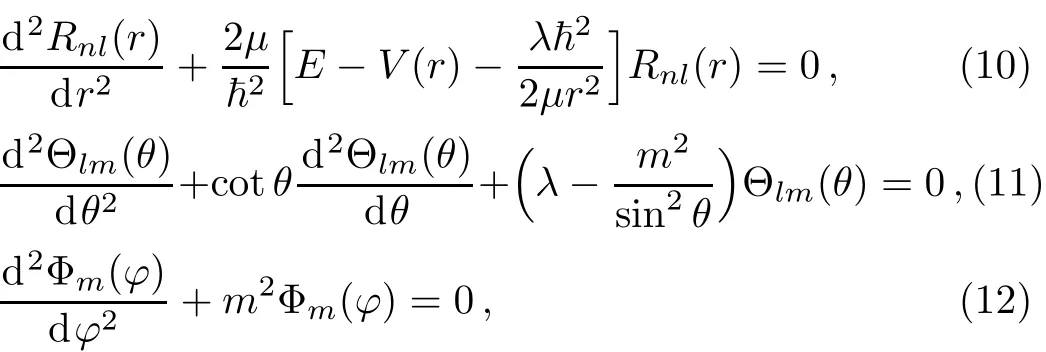
where λ=l(l+1)and m2are the separation constants.Ylm(θ,?)= Θlm(θ)Φm(?)is the solution of Eqs.(11)and(12)and their solutions are the well known spherical harmonic functions.[18]

4 Solutions of the Radial Schr¨odinger Equation

Equation(10)is the radial part of the Schr¨odinger equation,which we are interested in solving.The potential in Eq.(1)can be written as

where β =mg,α =k,z=r,δ=V0.We can also write Eq.(13)as

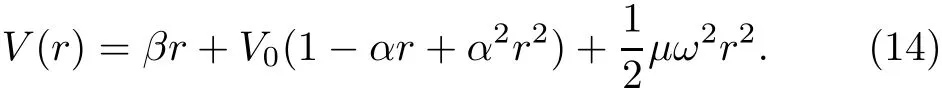
On arranging Eq.(14),we get our working potential amendable to NU method as

We show in Fig.1,the plot of the quantum gravitational potential as a function of r with various parameters of V0=0.5 fm?1,β = μ =1,ω =0.5 for α =0.2,0.4,and 0.6 respectively.The potential model of Eq.(15)can be used to solve various quantum mechanical equations such as the Schr¨odinger equation(SE),Klein–Gordon(KG)and Dirac equation using the NU method for their exact solutions.Writing Eq.(10)as

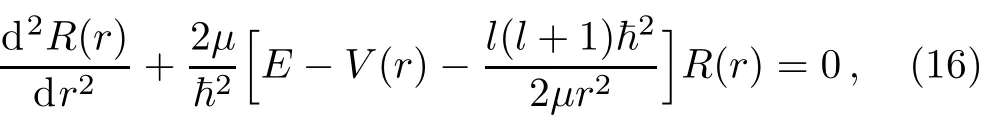
and using the potential of Eq.(15)in Eq.(16)yields,

Comparing Eq.(19)with Eq.(4)yields the following parameters,

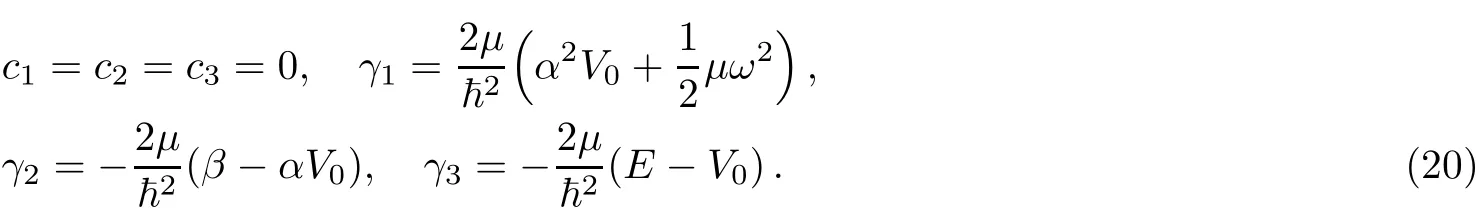
Other coeきcients are determined as,

Now using Eqs.(6),(20),and(21),we obtain the energy spectrum for the QMGP+HOP as

The weight function ρ(s)is obtained as,

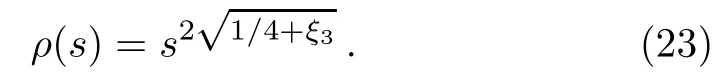
And we get the wave function χ(s)as

The radial wave function then becomes

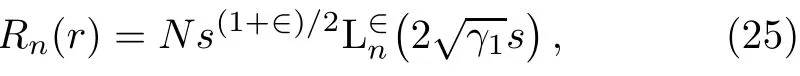
where N is the normalization constant.

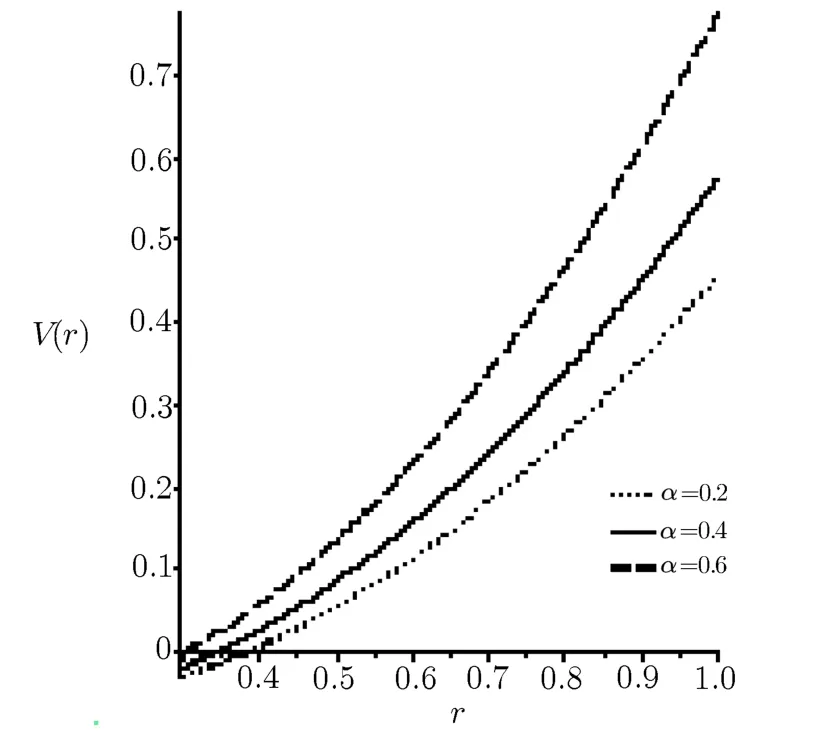
Fig.1 The plot of the potential gravitational potential Plus a harmonic potential as a function of r.

5 Discussion

Equation (22) is the energy eigen values for QMGP+HOP.If β=V0=0 in Eq.(13),the potential model turns back into the harmonic oscillator potential and the energy equation(22)yields the energy eigen values for the harmonic oscillator potential as,

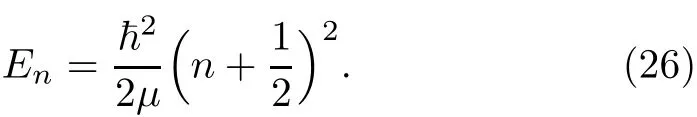
Equation(26)is similar to Eq.(35)of Ref.[19]obtained for the harmonic oscillator potential in electric f i eld when the f i eld strength ε was set to zero.In order to test the accuracy of our result,we computed numerically the energy level of equation(22)for various values of n with the following parameter sets of ω =0.5,V0=0.5 fm?1,μ=?=β=1 for α=0.2 and 0.4 respectively in Table 1.It is observed that the symmetry quantum gravitational potential diverges due to the behaviour of the harmonic potential at r→∞.However,the bound state wave function decays exponentially at large radius and leads to the convergent of the energy eigenvalues.

Table 1 Energy level for the quantum mechanical plus harmonic potential.

6 Conclusions

In summary,we have obtained the energy eigenvalues and the corresponding un-normalized wave function using the parametric NU method for the Schr¨odinger equation with the quantum mechanical gravitational potential plus the harmonic oscillator potential.A special case of the potential model has also been considered.

We acknowledge the anonymous reviewer for his/her comments which have improved the paper greatly.

[1]S.M.Ikhdair and R.Sever,Int.J.Mod.Phys.A 21(2006)6465.

[2]A.N.Ikot and L.E.Akpabio,Appl.Phys.Res.2(2010)202.

[3]B.I.Ita,Nig.J.Phys.20(2008)221.

[4]B.I.Ita,Int.J.Phys.Sci.2(2010)141.

[5]M.Hamzavi,S.M.Ikhdair,and B.I.Ita,Phys.Scr.85(2012)045007.

[6]A.N.Ikot,Chin.Phys.Lett.29(2012)060307.

[7]A.N.Ikot,O.A.Awoga,and B.I.Ita,J.At.Mol.Sci.3(2012)285.

[8]S.Dong and S.H.Dong,Phys.Scr.66(2002)342.

[9]F.Dominguez-Adame,Phys.Lett.A 136(1989)175.

[10]G.Paz,Eur.J.Phys.22(2001)337.

[11]M.N.Berberan-Santos,E.N.Bodunov,and L.Pogliani,J.Math.Chem.37(2005)101.

[12]B.I.Ita and A.I.Ikeuba,Open J.Microphys.(2013)(accepted for publication).

[13]P.Amore and F.M.Fernandez,Acta Polytechnica 50(2010)17.

[14]M.H.Jasim,R.A.K.Radhi,and M.K.A.Ameer,J.Phys.9(2011)90.

[15]A.N.Ikot,A.D.Antia,L.E.Akpabio,and J.A.Obu,J.Vect.Relat.6(2011)65.

[16]WANG Xue-Hong,GUO Jun-Yi,and LI Yan,Commun.Theor.Phys.58(2012)480.

[17]A.F.Nikiforov and V.B.Uvarov,Special Functions of Mathematical Physics,Birkhauser,Basel(1988).

[18]L.I.Scliあ,Quantum Mechanics,McGraw-Hill,New York(1955)

[19]S.M.Ikhdair,J.Mod.Phys.3(2012)170.