On the exponent of NmK2([Cpn])*
,
(School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China)(Received 22 November 2017: Revised 20 December 2017)
Abstract Let Cpn be the cyclic p-group of order pn and a finite field of characteristic p. For any integer 1≤l≤n, we obtain infinitely many non-trivial elements of order pl in NmK2([Cpn]). In fact, these elements form a generating set of NmK2([Cpn]) and the exponent of NmK2([Cpn]) is pn.
Keywords K-theory; Bass Nil groups; truncated polynomial
LetRbe a ring with unit. The Bass Nil groupsNmKi(R) are introduced by Bass[1]in order to investigate the relation betweenKi(R[x1,…,xm]) andKi(R). For anyi∈,NKi(R) is defined to be the kernel of surjective mapKi(R[x1])→Ki(R) induced byx1|→0. AndNmKi(R) is defined by iteration, i.e., the kernel of the surjectionNm-1Ki(R[xm])→Nm-1Ki(R) induced byxm|→0. Wheni=0,1,2,Ki(R) are the classical algebraicK-groups defined by Grothendieck[2], Bass[1]and Milnor[3], respectively. Wheni<0, the negativeK-theory is defined by Bass[1]. Wheni>2,Ki(R)=πi(K(R)) is defined to be thei-th homotopy group of theK-theory spaceK(R) which was first invented by Quillen[4]via plus-construction orQ-construction. As for the Bass Nil groups, the most known property is the following phenomenon.
TheoremA(See Refs. [5-9]). LetRbe a ring. For anyi,m∈andm≥1, ifNmKi(R)≠0, then it is not finitely generated as an abelian group.
Letpbe a prime number. In some cases,NKi(R) are abelianp-groups[8]. However, the exponents of these abelianp-groups are not completely determined. For example, the exponents ofNK0([C4]) andNK1([C4]) are both 2, but the exponent ofNK2([C4]) is still unknown[10].
K2([Cpn][x1,…,xm])?(1+N)mK2([Cpn])=
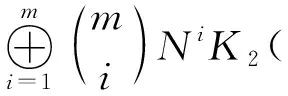
In Ref. [12], Juan-Pineda showed the non-finiteness ofNK2(p[Cpn]) by giving one non-trivial element of orderpand concluded thatNK2([C])≠0 for any non-trivial cyclic groupC. In this paper, we could give infinitely many non-trivial elements of orderplfor any 1≤l≤ninNmK2([Cpn]). In fact, we give a presentation ofNmK2([Cpn]) in terms of Dennis-Stein symbols and show that the exponent ofNmK2([Cpn]) ispn.
1 Main result
Lemma1.1NK2([Cpn])?K2([Cpn][x],J[x]).
ProofObserve that[Cpn][x]/J[x]?[x] and[x]→[Cpn][x] is a split inclusion. Sinceis a finite field,K2([Cpn])=K2()=0. AndK2([x])=K2()⊕NK2()=0 becauseis regular. Hence the result follows from the two exact sequences ofK-groups:
0→K2([Cpn][x],J[x])→K2([Cpn][x])
→K2([Cpn][x]/J[x])=0→0,
0→NK2([Cpn])→K2([Cpn][x])→
K2([Cpn])=0→0.
□
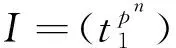
[Cpn]?[t1]/,
viaσ-1|→t1andxi|→ti+1. LetA=[t1,…,tm+1]/Iandbe its nilradical where. Then[x1,…,xm]?A/MandK2(A)?K2(A,M). So the above lemma becomesNK2([Cpn])?K2([t1,t2]/I,M) (m=1).

ProofIfk=1, the computation is easy. Supposepn-t-1+1≤k≤pn-t, the result follows from the inequalities

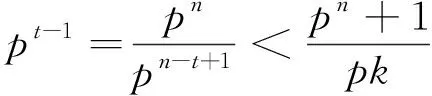
□
Theorem1.1LetCpnbe the cyclic group of orderpn(n≥1) generated byσ. For any integerm≥1,NmK2([Cpn])?⊕∞/pi) can be generated by these elements:


ProofSuppose we get a generating set ofK2([Cpn][x1,…,xm])?K2(A,M) in terms of Dennis-Stein symbols. Fixjdifferent indeterminates in {x1,…,xm}, say {xi1,…,xij}. The elements of the direct summandNjK2([Cpn])?K2([Cpn][xi1,…,xij])?K2([Cpn][x1,…,xm]) can be represented by using those Dennis-Stein symbols containing thesejdifferent indeterminates. HenceK2([Cpn][x1,…,xm]) containspieces ofNjK2([Cpn]). So the elements ofNmK2([Cpn]) can be represented by using those Dennis-Stein symbols inK2([Cpn][x1,…,xm]) containing all themindeterminates.
We follow the notations in Ref. [13]. Let={0,1,2…} be the set of non-negative integers and+={1,2,3,…} the set of positive integers. Letεi=(0,…,0,1,0,…,0)∈m+1be thei-th basis vector. Forα∈m+1, writetα…wheret1=σ-1 andti+1=xifor 1≤i≤m. Define

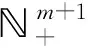
For (α,i)∈Λ′, let [α,i]=min{k∈|kα-εi∈Δ′} andw(α,i)=min{w∈|pw≥[α,i]}. Then [α,1]=「?, [α,j]=「? for anyj≠1. If gcd(p,α1,…,αm+1)=1, put [α]=max{[α,i]|αi?0 modp}. Set Λ′0={(α,i)∈Λ′| gcd(p,α1,…,αm+1)=1,i≠min{j|αj?0 modp,[α,j]=[α]}}, and let(α,i)∈Λ′0|[α,i]>1}.
Then by Corollary 2.7 in Ref. [13] and the above discussion,NmK2([Cpn]) has a presentation with
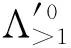
relations:pw(α,i)〈btα-εi,ti〉=0, wherew(α,i)=「logp[α,i]?.
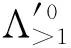



So one gets
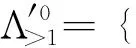
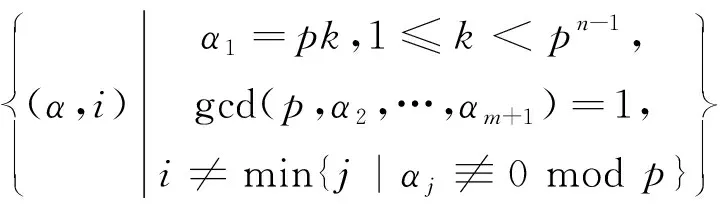


·〈b(σ-1)pk-1xβ,(σ-1)〉 where 1≤k≤pn-1and gcd(p,β1,…,βm)=1;
·〈b(σ-1)pkxβ-εi,xi〉 where 1≤k ·〈b(σ-1)pk-hxβ-εi,xi〉 where 1≤k≤pn-1,1≤h The relations are Then by Lemma 1.2, the result follows. □ Example2.1LetC4be the cyclic group of order 4 generated byσ. ThenNK2(2[C4])?⊕∞(/2⊕/4) can be generated by these elements: the generators of order 4 are {〈(σ-1)xi-1,x〉|i≥1}, {〈(σ-1)x2i-1,(σ-1)〉|i≥1}, and the generators of order 2 are {〈(σ-1)3xi-1,x〉|i≥1}, {〈(σ-1)3x2i-1,(σ-1)〉|i≥1}. N2K2(2[C4])?⊕∞(/2⊕/4) can be generated by these elements: the generators of order 4 are {〈(σ-1)xi-1yj,x〉|i≥1,j≥1}, {〈(σ-1)xiyj-1,y〉|i≥1,j≥1}, {〈(σ-1)x2i-1yj,(σ-1)〉|i≥1,j≥1}, {〈(σ-1)x2iy2j-1,(σ-1)〉|i≥1,j≥1}, and the generators of order 2 are {〈(σ-1)3xi-1yj,x〉|i≥1,j≥1}, {〈(σ-1)3xiyj-1,y〉|i≥1,j≥1}, {〈(σ-1)2x2i-1y2j-1,x〉|i≥1,j≥1}, {〈(σ-1)2x2i-1yj-1,y〉|i≥1,j≥1}, {〈(σ-1)3x2i-1yj,(σ-1)〉|i≥1,j≥1}, {〈(σ-1)3x2iy2j-1,(σ-1)〉|i≥1,j≥1}, wherex,yare indeterminates. Corollary2.1NK1([Cp2])?⊕∞/p. ProofAssumeCp2is generated byσ. There is a Milnor square, whereζp2is a primitivep2-th root of unity and[ζp2] is the ring of integers in(ζp2). By the Mayer-Vietoris sequence forNK-functors, we get an exact sequence NK2([Cp2])→NK2([ζp2])⊕ NK2([Cp])→NK2(p[Cp])→ NK1([Cp2])→NK1([ζp2])⊕NK1([Cp]). NK2([Cp])→NK2(p[Cp])→ NK1([Cp2])→0. Moreover, we haveNK2(p[Cp])?⊕∞/pandNK1([Cp2])≠0 (see Ref. [14]). HenceNK1([Cp2]) is not finitely generated, therefore NK1([Cp2])?⊕∞/p. □

2 Examples

 中國科學(xué)院大學(xué)學(xué)報(bào)2019年1期
中國科學(xué)院大學(xué)學(xué)報(bào)2019年1期
