具有局部弱穩(wěn)定退化解二階非線性方程的奇攝動(dòng)問(wèn)題
秦趙娜,姚靜蓀
(安徽師范大學(xué) 數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽 蕪湖 241003)
0 引 言
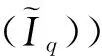
解的存在性及其漸近估計(jì).

(3)
則稱退化方程F(t,u,u′)=0的解u=u(t)在[a,b]上是(Iq)穩(wěn)定的.

且在D0(u)∩([a,a+δ1]×)中,在D0(u)∩([b-δ1,b]×)中,則稱退化方程F(t,u,u′)=0的解u=u(t)在[a,b]上是穩(wěn)定的.
定義3如果存在常數(shù)δ2>0,使得當(dāng)u(a)≠A時(shí),在D(u)∩([a,a+δ2/2]×2)中,Fy′(t,y,y′)≤0,且當(dāng)u(b)≠B時(shí),在D(u)∩([b-δ2/2,b]×2)中,Fy′(t,y,y′)≥0,其中D(u)∶={(t,y,y′)|a≤t≤b,|y-u(t)|≤d(t),|y′|<+∞},d(t)由式(3)給出.則稱退化方程F(t,u,u′)=0的解u=u(t)是局部弱穩(wěn)定的.
假設(shè):
(H1) 退化方程F(t,u,u′)=0具有解u=u(t)∈C2[a,b],且u=u(t)是局部弱穩(wěn)定的;
(H2)F,Fy,Fy′∈C(D(u)),Fy′(t,y,y′)在[a,b]×2上是有界函數(shù).
1 主要結(jié)果
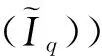
|y(t,ε)-u(t)|≤WL(t,ε)+WR(t,ε)+Γ(ε),
其中:
σ=m1/2q[(q+1)(2q+1)!]-1/2;r>0為待定正常數(shù).
證明: 不妨設(shè)u(a)≠A,u(b)≠B.用EST表示指數(shù)型小項(xiàng).
1) 當(dāng)u=u(t)在[a,b]上是(Iq)穩(wěn)定時(shí),令α(t,ε)=u(t)-WL(t,ε)-WR(t,ε)-Γ(ε),β(t,ε)=u(t)+WL(t,ε)+WR(t,ε)+Γ(ε).顯然
α(t,ε)≤β(t,ε),α(a,ε)≤A≤β(a,ε),α(b,ε)≤B≤β(b,ε).
(4)
令δ0=min{δ1,δ2,(b-a)/2},其中δ1,δ2分別由定義1和定義3給出.下證
εβ″-F(t,β,β′)≤0,
(5)
εα″-F(t,α,α′)≥0,
(6)

當(dāng)t∈[a,b-δ0/2]時(shí),
(7)
當(dāng)t∈[a+δ0/2,b]時(shí),
(8)
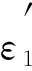
r=2C1+‖u″‖.
(9)

Γ(ε)≤δ1/2.
(10)

WR≤δ1/2.
(11)

當(dāng)t∈[b-δ0/2,b]時(shí),同理存在ε2>0,使得對(duì)式(9)給定的r>0,當(dāng)0<ε≤ε2時(shí),式(5)成立.

令ε0=min{ε1,ε2,ε3},對(duì)式(9)給定的r>0,當(dāng)0<ε≤ε0時(shí),對(duì)一切t∈[a,b]都有式(5)成立.
同理對(duì)式(9)給定的r>0,當(dāng)0<ε≤ε0時(shí),對(duì)一切t∈[a,b]式(6)也成立.于是,由(H2)根據(jù)文獻(xiàn)[9]中引理2.2.1知,在(Iq)穩(wěn)定的條件下結(jié)論成立.


當(dāng)t∈[a,b-δ0/2]時(shí),式(7)成立,且
(12)
當(dāng)t∈[a+δ0/2,b]時(shí),式(8)成立,且
(13)

取
r=2(C2+‖u″‖).
(14)
當(dāng)t∈[a,a+δ0/2]時(shí),

當(dāng)t∈[b-δ0/2,b]時(shí),同理存在ε5>0,使得對(duì)式(14)式給定的r>0,當(dāng)0<ε≤ε5時(shí),式(5)成立.當(dāng)t∈[a+δ0/2,b-δ0/2]時(shí),
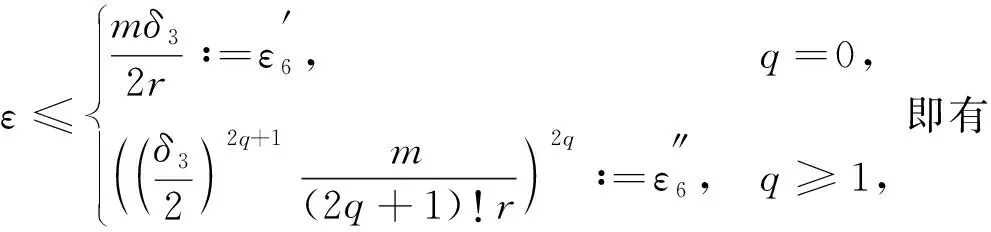
Γ(ε)≤δ3/2.
(15)

WL+WR≤δ3/2.
(16)

故對(duì)式(14)給定的r>0,當(dāng)0<ε≤min{ε4,ε5,ε6}時(shí),對(duì)一切t∈[a,b]都有式(5)成立.
另一方面,當(dāng)t∈[a+δ0/2,b-δ0/2]時(shí),
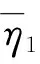
當(dāng)t∈[a,a+δ0/2]∪[b-δ0/2,b]時(shí),




綜上所述,令ε0=min{ε4,ε5,ε6,ε7},對(duì)式(14)給定的r>0,當(dāng)0<ε≤ε0時(shí),對(duì)一切t∈[a,b]都有式(4)~(6)成立.于是由(H2),根據(jù)文獻(xiàn)[9]中引理2.2.1知情形①成立.
② 當(dāng)A>u(a),B (17) (18) (19) (20) (21) (22) r=2[C3(1+M2)+‖u″‖]. (23) 當(dāng)t∈[a+δ0/2,b-δ0/2]時(shí), 根據(jù)式(18)同理可證,對(duì)式(23)給定的r>0,當(dāng)0<ε≤ε8時(shí),式(6)成立. 當(dāng)t∈[a,a+δ0/2]時(shí), 同理可證當(dāng)t∈[b-δ0/2,b]時(shí),對(duì)上述的ε9>0及式(23)給定的r>0,當(dāng)0<ε≤ε9時(shí),式(6)成立. εβ″-F(t,β,β′)≤ε(u″+C3+M2C3)-Γ(m-M2Γ)≤0; 根據(jù)式(21),(22)同理可證,對(duì)式(23)給定的r>0,存在ε11>0,使得當(dāng)0<ε≤ε11時(shí),對(duì)t∈[a,a+δ0/2]都有式(6)成立. 綜上所述,令ε0=min{ε8,ε9,ε10,ε11},對(duì)上述取定的r>0,當(dāng)0<ε≤ε0時(shí),對(duì)一切t∈[a,b]都有式(4)~(6)成立.于是由(H2)根據(jù)文獻(xiàn)[9]中引理2.2.1知,情形②得證. ③ 當(dāng)A ④ 當(dāng)A 作為問(wèn)題(1)-(2)的特例,對(duì)二階半線性問(wèn)題: 和二階擬線性問(wèn)題: 應(yīng)用定理1得到的結(jié)果與文獻(xiàn)[6]的結(jié)論一致. 例1 例2 |y(t,ε)-u(t)|≤WL(t,ε)+WR(t,ε)+Γ(ε), [1] YAO Jing-sun.Asymptotic Solution of the Three Points Boundary Value Problem for Nonlinear Third Order Equation [J].Mathematica Applicata,2009,22(2): 437-442. [2] YAO Jing-sun,MO Jia-qi,CHEN Xiu.The Solvability for Singularly Perturbed Quasi-linear Differential System of Second Order [J].J of Math,2010,30(6): 959-965. [3] WU You-ping,YAO Jing-sun,ZHUANG Hong-yan.A Class of Singularly Perturbed Problem with Two Parameters and Nonlinear Boundary Value Conditions [J].Applied Mathematics A Journal of Chinese Universities: Ser A,2011,26(3): 288-294.(吳有萍,姚靜蓀,莊紅艷.一類具非線性邊值條件的雙參數(shù)奇攝動(dòng)問(wèn)題 [J].高校應(yīng)用數(shù)學(xué)學(xué)報(bào): A輯,2011,26(3): 288-294.) [4] CHEN Ting,YAO Jing-sun.The Shock Solution for a Class of Quasilinear Singularly Perturbed Boundary Value Problems [J].Chin Quart J of Math,2012,27(3): 317-322. [5] LIU Yan,YAO Jing-sun.A Class of Singular Perturbed Problems with Nonlinear Boundary Value Conditions for Higher Order Equations [J].Applied Mathematics A Journal of Chinese Universities: Ser A,2012,27(2): 175-181.(劉燕,姚靜蓀.一類高階方程的非線性邊界條件的奇攝動(dòng)問(wèn)題 [J].高校應(yīng)用數(shù)學(xué)學(xué)報(bào): A輯,2012,27(2): 175-181.) [6] Chang K W,Howes F A.Nonlinear Singular Perturbation Phenomena:Theory and Applications [M].New York: Springer-Verlag,1984: 6-66. [7] 林宗池,周明儒.應(yīng)用數(shù)學(xué)中的攝動(dòng)方法 [M].南京: 江蘇教育出版社,1995: 205-222. [8] ZHOU Ming-ru.Boundary and Corner Layer Behavior in Singularly Perturbed Robin Boundary Value Problem [J].Ann of Diff Eqs,2005,21(4): 639-647. [9] 劉樹(shù)德,魯世平,姚靜蓀,等.奇異攝動(dòng)邊界層和內(nèi)層理論 [M].北京: 科學(xué)出版社,2012: 15-40. [10] LI Qing,YAO Jing-sun.Singularly Perturbed Problem for the Second-Order Nonlinear Equation with a Locally Strongly Stable Reduce Solution [J].Journal of Anhui Normal University: Natural Science,2012,31(6): 514-518.(李青,姚靜蓀.具有局部強(qiáng)穩(wěn)定退化解的二階非線性方程奇攝動(dòng)問(wèn)題 [J].安徽師范大學(xué)學(xué)報(bào): 自然科學(xué)版,2012,31(6): 514-518.)

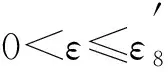

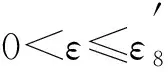









2 應(yīng)用實(shí)例




