田德生

(湖北工業(yè)大學(xué)理學(xué)院,湖北武漢 430068)

三階常系數(shù)擬線性泛函微分方程的周期解

田德生

(湖北工業(yè)大學(xué)理學(xué)院,湖北武漢 430068)

研究了一個(gè)三階泛函微分方程周期解的存在唯一性和全局吸引性:

這是一個(gè)常系數(shù)擬線性泛函微分方程.通過(guò)將這個(gè)方程轉(zhuǎn)變?yōu)槿S的擬線性微分方程(組),得到了這個(gè)方程存在唯一周期解的充分條件;通過(guò)選取適當(dāng)?shù)睦钛牌罩Z夫函數(shù),推導(dǎo)了這個(gè)方程解的全局吸引性;進(jìn)一步,得到了此方程周期解的全局吸引性.最后,舉出了兩個(gè)應(yīng)用實(shí)例.

泛函微分方程;周期解;唯一性;全局吸引性

1 引言

考慮三階泛函微分方程:

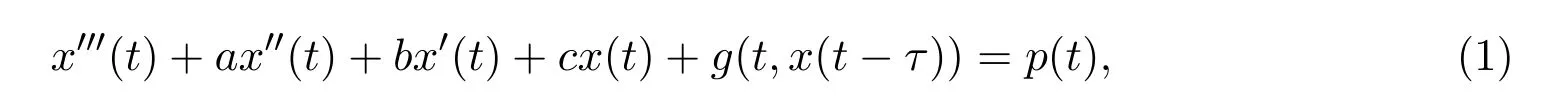
其中a,b,c,τ∈R(τ＞0)為常數(shù);p(t)∈C(R,R)具有周期為T-函數(shù)(T為正常數(shù)); g∈C(R2,R)關(guān)于第一個(gè)變量為T-周期函數(shù).本文研究此方程周期解的存在唯一性及全局吸引性.

近年來(lái),三階微分方程周期解的問(wèn)題得到了廣泛研究[19],所應(yīng)用的研究方法也是多種多樣.文獻(xiàn)[1-3]對(duì)如下微分方程周期解的問(wèn)題做了許多研究工作:

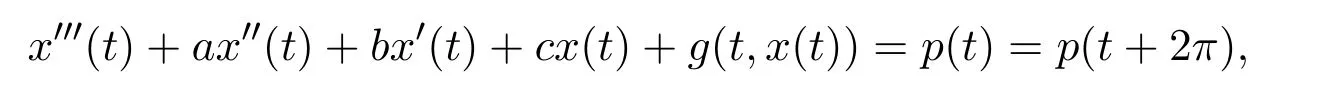
得到了方程在多種情況下周期解的存在性;文獻(xiàn)[4-6]應(yīng)用各種不動(dòng)點(diǎn)定理,研究了三階微分方程周期解的存在性問(wèn)題;文獻(xiàn)[7]應(yīng)用Leray-Schauder非線性選擇性原理的方法,研究了多種形式三階微分方程的周期解問(wèn)題;文獻(xiàn)[8-9]應(yīng)用重合度理論的延拓定理,分別研究了下面兩個(gè)形式的三階微分方程周期解的存在性問(wèn)題:

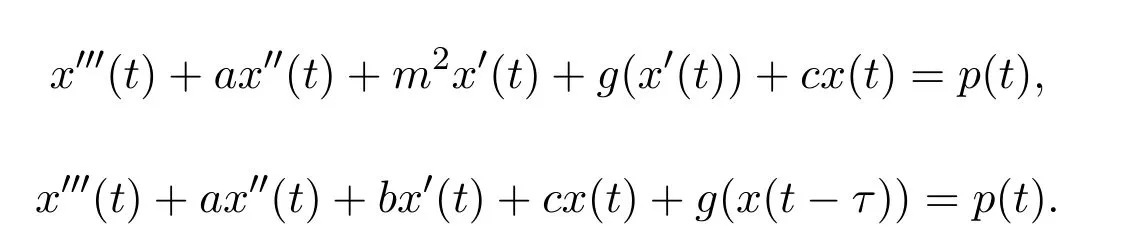
隨著人們利用計(jì)算機(jī)對(duì)微分方程解數(shù)值計(jì)算的應(yīng)用和普及,越來(lái)越迫切地要求人們研究微分方程解的存在唯一性和吸引性.而且,就現(xiàn)有的文獻(xiàn)看,對(duì)三階微分方程周期解的存在唯一性和全局吸引性問(wèn)題的研究成果尚不多見(jiàn).因此,本文對(duì)方程(1)周期解問(wèn)題的研究是十分有意義的.

目前,許多數(shù)學(xué)工作者研究了生物模型周期解的全局吸引性問(wèn)題[10-12],他們的研究方法主要是選擇適當(dāng)?shù)睦钛牌罩Z夫函數(shù),計(jì)算右上狄尼導(dǎo)數(shù).本文將采用計(jì)算左上狄尼導(dǎo)數(shù)的方法,研究方程周期解的全局吸引性,這與他們的研究方法是不同的.一般地,計(jì)算右上導(dǎo)數(shù)的方法,需要估計(jì)李雅普諾夫函數(shù)的右上導(dǎo)數(shù)在無(wú)限區(qū)間[0,+∞)上的符號(hào);而計(jì)算左上導(dǎo)數(shù)的方法,只需估計(jì)左上導(dǎo)數(shù)在某個(gè)有限區(qū)間[0,Ti]上的符號(hào)(詳見(jiàn)定理3.1的證明).因此,本文采用的計(jì)算左上導(dǎo)數(shù)的方法更為簡(jiǎn)潔.

2 周期解的存在唯一性

在這一節(jié),討論方程(1)周期解的存在唯一性.首先,介紹本文所用到的引理,它是文獻(xiàn)[13]中的定理3.考慮擬線性方程:

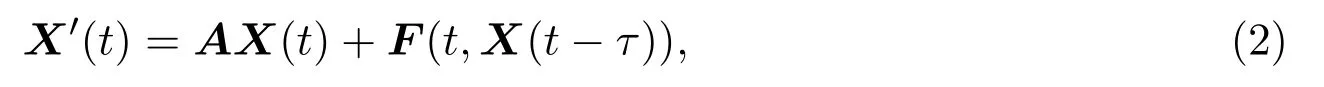
其中X∈C(R,Rn),t∈R為變量,A∈Rn×n為常數(shù)矩陣,F∈C(R×Rn,Rn)關(guān)于第一個(gè)變量為T-周期函數(shù),τ∈R為常數(shù).

引理2.1設(shè)T‖A‖＜2π,detA/=0,又設(shè)存在一個(gè)常數(shù)L≥0,它滿足

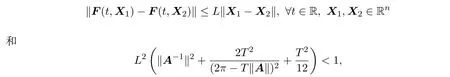
則方程(2)有唯一的T-周期解.這里,矩陣范數(shù)‖A‖是由向量范數(shù)‖X‖引導(dǎo)的,A∈Rn×n, X∈Rn.

在下面的討論中,約定如下的向量范數(shù)和矩陣范數(shù):

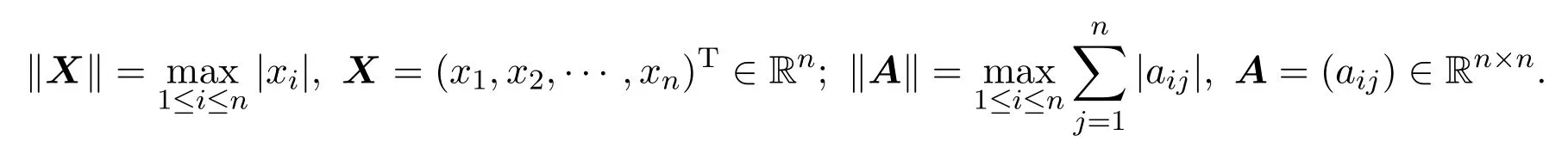
定理2.1設(shè)

(H1)存在常數(shù)L≥0,滿足

那么方程(1)有唯一的T-周期解.

證明類似于定理2.1的證明,此處略去.

3 全局吸引性

在這一節(jié),研究方程(1)的解和周期解的全局吸引性.在這里指出,說(shuō)方程(1)的一個(gè)解x?(t)是全局吸引的,如果方程(1)的其它任意解x(t)與x?(t)滿足如下的關(guān)系:

4 應(yīng)用實(shí)例

最后提出:滿足定理2.1條件的周期解是否也具有全局吸引性?這將是下一步的研究工作.

致謝作者對(duì)審稿專家提出的寶貴修改意見(jiàn)表示真誠(chéng)的感謝!

[1]Ezeilo J O C.On the existence of periodic solution of a certain third-order differential equation[J].Pro. Cambridge Philos.Soc.,1960,56:381-389.

[2]Sedziwy S.On periodic solution of a certain third-order nonlinear differential equation[J].Ann.Polon Math., 1965,17:147-154.

[3]Afuwape A U,Omari P,Zanolin F.Nonlinear perturbation of differential operators with nontrivial kernel and application to third-order periodic boundary value problems[J].J.Math.Anal.Appl.,1989,143:35-56.

[4]Chu J,Zhou Z.Positive solutions for singular non-linear third-order periodic boundary value problems[J]. Nonlinear Analysis,2006,64:1528-1542.

[5]Feng Y.On the existence and multiplicity of positive periodic solutions of a nonlinear third-order equation[J]. Appl.Math.Lett.,2009,22:1220-1224.

[6]Prasad K R,Murali P.Multiple positive solutions for nonlinear third order general three-point boundary value problems[J].Differential Equations and Dynamical Systems,2008,16:63-75.

[7]John R G,Chattanooga.Positive solutions for third order multi-point singular boundary value problems[J]. Czechoslovak Math.J.,2010,60:173-182.

[8]Zhang Z,Wang Z,Yu J.On the existence of periodic solutions of third order functional differential equations[J].Funkcialaj Ekvacioj,2000,43:461-469.

[9]Amster P,P De N′apoli,Mariani M C.Periodic solutions of a resonant third-order equation[J].Nonlinear Analysis,2005,60:399-410.

[10]Wang Q,Jizhou.Existence and attractivity of a periodic solution for a ratio-dependent Leslie system with feedback controls[J].Nonlinear Analysis:RWA,2011,12:24-33.

[11]Zhang Z,Wang H.Existence and global attractivity of positive periodic solutions for a generalized predatorprey system with time delay[J].Math.and Computer Modelling,2006,44:188-203.

[12]Li Zhong,Chen F,He M.Permanence and global attractivity of a periodic predator-prey system with mutual interference and impulses[J].Nonlinear Sci.Numer.Simulat.,2012,17:444-453.

[13]馬世旺,庾建設(shè),王志成.擬線性泛函微分方程周期解的存在唯一性[J].數(shù)學(xué)年刊:A輯,2001,22(1):105-110.

Periodic solution of a third-order quasilinear functional differential equation with constant coefficients

Tian Desheng

(College of Sciences,Hubei University of Technology,Wuhan 430068,China)

This paper considers the existence,uniqueness and global attractivity of a periodic solution for a third-order functional differential equation:

which is a third-order quasilinear functional differential equation with constant coeffcients.By converting this equation into a three-dimensional quasilinear one,the sufficient conditions for the existence of exactly one periodic solution of this equation are established.By constructing suitable Lyapunov functionals,the global attractivity of a solution for the above equation is established;Moreover,the global attractivity of a periodic solution is established.In the last section,two examples will be provided to illustrate the applications of the results.

functional differential equation,periodic solution,uniqueness,global attractivity

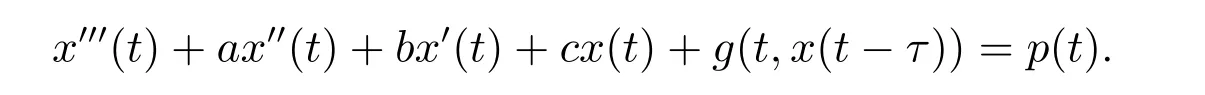
O175

A

1008-5513(2013)03-0233-08

10.3969/j.issn.1008-5513.2013.03.003

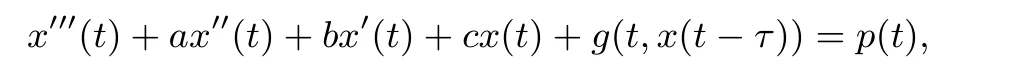
2013-03-18.

田德生(1966-),博士,教授,研究方向:常微分方程理論及其應(yīng)用,生物數(shù)學(xué).

2010 MSC:34K13