杜保建,何朝兵,袁付順

(安陽師范學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)院,中國 安陽 455000)

在馬氏過程理論中,強(qiáng)馬氏性是一個非常重要的基本概念.而兩參數(shù)隨機(jī)過程的強(qiáng)馬氏性的時間變化分為隨機(jī)的[1]和非隨機(jī)的[2-5].文獻(xiàn)[2，4～5]提出了寬過去強(qiáng)馬氏性和平面上的*-強(qiáng)馬氏性的一般定義.討論了各種強(qiáng)馬氏性之間的關(guān)系,這些強(qiáng)馬氏性的參數(shù)變化是非隨機(jī)的.對參數(shù)變化為隨機(jī)的情況,至今還沒有人研究.文獻(xiàn)[7～10]研究了停點的各種定義及性質(zhì).由于兩參數(shù)*-馬氏過程具有良好的性質(zhì)[6],所以本文對*-馬氏過程提出參數(shù)變化為隨機(jī)的*-強(qiáng)馬氏過程的一般定義是十分必要的,本文還給出了*-馬氏過程為*-強(qiáng)右選馬氏過程的一個充分條件,研究了各種*-強(qiáng)馬氏性之間的關(guān)系,創(chuàng)造性地推廣了文獻(xiàn)[1]中相應(yīng)結(jié)果.

對r∈K-T,令Xr=c(E中某個固定點),可使X擴(kuò)張定義于K上,對于(E,ε)上的*-轉(zhuǎn)移函數(shù)(P1,P2,P)如下擴(kuò)張定義于K上:

這樣P(s,t,s′,t′,x,y,z,B)就定義在(s,t),(s′,t′)∈K,(s,t)≤(s′,t′),x,y,z∈E,B∈ε上,后面有時把P也記為P((s,t),(s′,t′),x,y,z,B),以后提到擴(kuò)張到K上的(Xr)及P時,都是指上述擴(kuò)張.

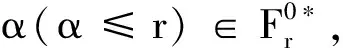
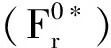
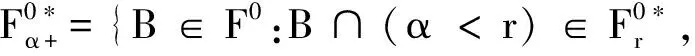
2 平面上*-強(qiáng)馬氏性的一般定義

(1)對固定的B∈ε,映射(s,t,s′,t′,x,y,z)→P(s,t,s′,t′,x,y,z,B)為[B(K)]2×ε3可測的;

則稱X為*-強(qiáng)μ0馬氏過程.

(1)同定義1 中(1);

則稱X為*-強(qiáng)右μ0馬氏過程.

(1)同定義1 中(1);

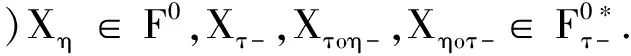
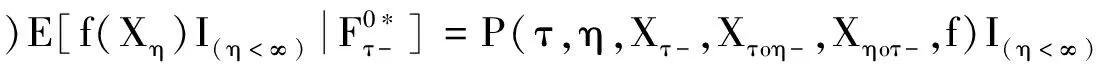
則稱X為*-強(qiáng)左μ0馬氏過程.

下面的定理1 給出了馬氏過程為*-強(qiáng)右O0*馬氏過程的一個充分條件.

則X是*-強(qiáng)右O0*馬氏過程.

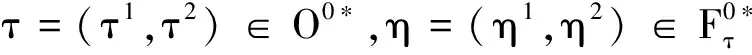
(1)

令

令n→+∞,由已知條件可得(1)式成立,由L-系方法可證對任意f∈bε,(1) 式也成立.

推論OUP2過程和右連續(xù)兩指標(biāo)獨立增量過程都是*-強(qiáng)右O0*馬氏過程.

由文獻(xiàn)[1]和文獻(xiàn)[6]給出的OUP2過程的*-轉(zhuǎn)移函數(shù)和獨立增量過程的*-轉(zhuǎn)移函數(shù)可知P(s,t,s′,t′,x,y,z,B)關(guān)于(s,t,s′,t′,x,y,z)是連續(xù)函數(shù),從而推論成立.

在完備化情況,定理1是*-強(qiáng)右選馬氏性的一個充分條件,這時軌道在T上右連續(xù)可改為a.s.右連續(xù).

為簡單起見,下面只考慮完備化情況.

3 各種*-強(qiáng)馬氏性之間的關(guān)系

由定義易證如下兩個定理.

定理2設(shè)μ1和μ2是2個μ類函數(shù)集,μ1?μ2.則每個*-強(qiáng)(強(qiáng)左,強(qiáng)右)μ2馬氏過程是*-強(qiáng)(強(qiáng)左,強(qiáng)右)μ1馬氏過程.

證因為X適應(yīng)右連續(xù),所以X寬過去循序可測,由文獻(xiàn)[2]中定理3.1可知X具有*-強(qiáng)μ可測性.由定義2中強(qiáng)右μ馬氏性得

與文獻(xiàn)[1]中不同,對于τ∈O*,存在A,使τA為可及點和τAc為絕不可及點,但ηA不一定是可及點(當(dāng)η=τ+(h,l)時成立,其中h>0,l>0為常數(shù)).因此,我們未能得到:X是*-強(qiáng)(強(qiáng)右)選馬氏過程,當(dāng)且僅當(dāng)X同時為*-強(qiáng)(強(qiáng)右)及和*-強(qiáng)(強(qiáng)右)不及馬氏過程.

參考文獻(xiàn)：

[1] 侯 強(qiáng).兩指標(biāo)馬爾科夫過程的停點變換[J].西北電訊工程學(xué)院學(xué)報,1986(3):13-20.

[2] 周健偉.平面上的強(qiáng)Markov性[J].數(shù)理統(tǒng)計與應(yīng)用概率,1994,9(4):78-83.

[3] 王梓坤.二參數(shù)ORNSTEIN-UHIENBECK過程[J].數(shù)學(xué)物理學(xué)報,1983,4(3):395-406.

[4] 周健偉.兩指標(biāo)過程的強(qiáng)馬爾科夫性[J].應(yīng)用概率統(tǒng)計,1986,2(4):302-306.

[5] 周健偉.兩指標(biāo)強(qiáng)馬爾科夫過程[J].華東師范大學(xué)學(xué)報,1989,4(4):7-11.

[6] LUO S J.Two-parameter homogeneous Markovion processes[J].Acta Math Sci,1988,8(3):315-322.

[7] 杜保建.兩指標(biāo)過程的寬過去強(qiáng)Markov性[J].數(shù)理統(tǒng)計與應(yīng)用概率,1995,10(4):25-30.

[8] 任曉紅,陳慧嬋,張卓奎.強(qiáng)鞅的停止性質(zhì)[J].吉林大學(xué)學(xué)報：理學(xué)版,2003,41(2):463-465.

[9] 張卓奎,任曉紅,陳慧嬋.兩指標(biāo)停時及其性質(zhì)[J].吉林大學(xué)學(xué)報：理學(xué)版,2002,40(2):127-130.

[10] 王生喜.N指標(biāo)隨機(jī)過程的停止[J].新疆大學(xué)學(xué)報：自然科學(xué)版,2003,20(1):26-28.