魯三芽, 龍 芳

(1.南昌工程學院理學系,江西南昌 330029; 2.江西機電職業(yè)技術學院基礎部,江西南昌 330013)

單葉解析函數的幾個子族之間的關系及應用

魯三芽1, 龍 芳2

(1.南昌工程學院理學系,江西南昌 330029; 2.江西機電職業(yè)技術學院基礎部,江西南昌 330013)

在復平面單位圓盤內引入了β型螺形函數族^Sβ的一個子類^Sβα函數族,研究了^Sβα族與解析函數族S＊,S＊(α),K,K(α)及^Sβ之間的關系,利用得到的關系式對^Sβα族的第二項系數進行了精確估計,同時得到了K(α)族的第二、三項系數的關系式和^Sβ族的一個積分表示式,推廣了一些作者的結果.

星形函數;凸函數;β型螺形函數;^Sβα函數族;系數估計

1 定義及記號

Robertson在文[1]中引入S＊的一個子族α次星形函數.

定義1 設α∈[0,1).若f∈S且滿足

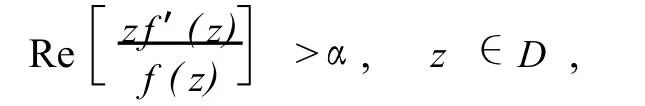
則稱f為α次星形函數.記其族為S＊(α).

Spacek在文[2]中對星形函數族S＊進行了推廣,得到了β型螺形函數族^Sβ,并給出了定義在D上的^Sβ函數族的一個解析刻畫.

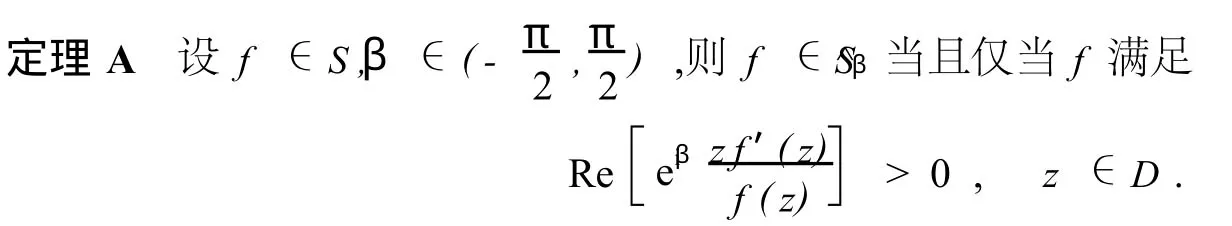
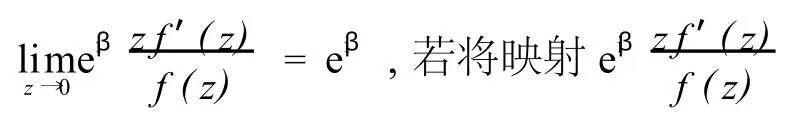
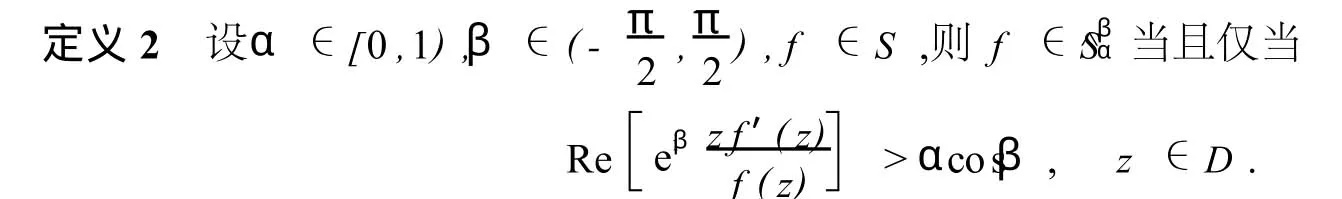
顯然,當β=0時,f∈S＊(α);當α=0時,f∈^Sβ;當α=β=0時,f∈S＊.

2 引理及說明

為證明本文的主要結果,需要以下引理.

引理1[3]設α∈[0,1),f∈S,z∈D,則下列結論成立：

注 引理1給出了S＊(α)與S＊,K(α)和S＊之間的關系.

引理2 設α∈[0,1),f∈S,z∈D,則下列結論成立：

(i)[3-4]f(z)∈K當且僅當存在g(z)∈S＊,使g(z)=zf′(z);

(ii)[3]f∈K(α)當且僅當存在h(z)∈S＊(α),使h(z)=zf′(z).

注 引理2給出了K與S＊,K(α)與S＊(α)之間的關系,是Alexander定理及其推廣.

3 主要結果及其證明

定理1,定理2和定理3給出的是一些等價關系,在實際中具有很好的應用.限于篇幅,本文只舉證了幾個應用.

(i)f(z)∈S＊(α)當且僅當存在g(z)∈K,使f(z)=z[g′(z)]1-α,其中冪函數取滿足[g′(z)]1-α|z=0=1的解析分支;

(ii)f(z)∈S＊(α)當且僅當存在h(z))∈^Sβ,使

證(i)由引理1(i)和引理2(i)可得證.

(ii)由引理1(i)和引理4可得證.

注 定理1溝通了S＊(α),K和^Sβ之間的等價關系.

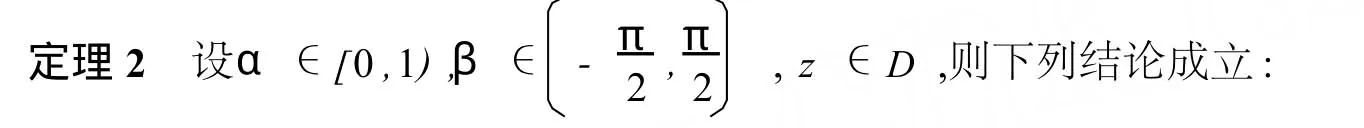
(i)f(z)∈K(α)當且僅當存在g(z)∈K,使f′(z)=[g′(z)]1-α,其中冪函數取滿足[g′(z)]1-α|z=0=1的解析分支;

(iii)f(z)∈^Sβ當且僅當存在u(z)∈K,使f(z)=z[u′(z)]e-iβcosβ,其中冪函數取滿足[u′(z)]e-iβcosβ|z=0=1的解析分支.

證(i)由引理1(ii)和引理2(i)可得證.

(ii)由引理1(ii)和引理4可得證.

(iii)由(i),(ii)可得證.

注 定理2給出了K,K(α)和^Sβ之間的等價關系.

(ii)由(i)和引理1(i)可得證.

(iii)由(i)和定理1(i)可得證.

(iv)由(i)和引理2(ii)可得證.

(v)由(i)和定理1(ii)可得證.

定理4 函數

注 定理6推廣了文[6],[7]的相應結果.當α=0時,f∈K,定理6恰為引理6的結論.

[1] Robertson M S.On the theory of univalent functions[J].Ann.Math.,1936,37：374-408.

[2] Spacek L.Contribution a la theorie des fonctions univalentes[J].Casopis Pest Math.,1932,62：12-19(in Russia).

[3] Graham I,Kohr G.Geometric function theory in one and higher dimensions[M].New York：Marcel Dekker,2003：54-78.

[4] Pommerenke C H.Univalent functions[M].Gottingen：Vandenhoeck&Ruprecht,1975：39-41.

[5] Goodman A W.Univalent functions,Ⅰ-Ⅱ[M].Tampa Florida：Mariner Publ.Co.,1983：148-154.

[6] Nehari Z.The Schwarzian derivative and schlicht functions[J].Bull.Amer.Math.,1949,55：545-551.

[7] Koepf W.Convex functions and the Nehari univalence criterion[J].Ann.Acad.Sci.Fenn.,Ser.A I Math.,1983,8：349-355.

Applications of Relationships Among the Several Subclasses of Univalent Analysis Functions

L U S an-ya1, LON G Fang2
(1.Department of Science Faculty,Nanchang Institute of Technology,Nanchang 330099,China;
2.Basic Department of Jiangxi Vocational College of Mechanical and Electrical Technology,Nanchang 330013,China)

A subclass of spirallike functions of typeβdenoted by^Sβαis introduced in the unit disc of the complex plane. We investigate the relationships among the class of^Sβαand the analysis function classes：S＊,S＊(α),K,K(α)and^Sβ. With the relationship equations we get,we sharply estimate the second coefficient of^Sβα.In addition,we obtain the relative equation between the second and the third coefficient ofK(α)class and the integral representation of^Sβclass, which generlizes the related results of some authors.

starlike functions;convex functions;spirallike functions of typeβ;functions class of^Sβα;coefficient estimate

O174.52

A

1672-1454(2011)03-0087-06

2008-09-22

江西省自然科學基金項目(2007GZS0177);江西省教育廳科學技術研究項目(GJJ09149)