李丹青

(電子科技大學(xué)數(shù)學(xué)科學(xué)學(xué)院,成都 611731)

非負(fù)矩陣譜半徑的一個(gè)新界值

李丹青

(電子科技大學(xué)數(shù)學(xué)科學(xué)學(xué)院,成都 611731)

在Wielandt定理的基礎(chǔ)上進(jìn)行了推廣,得到了一種估計(jì)非負(fù)矩陣譜半徑的新方法,數(shù)值例子顯示了新方法所得到的結(jié)果更為精確.

非負(fù)矩陣;譜半徑;界

1 引 言

矩陣A=(aij)∈Rn×n的n個(gè)特征值λ1,λ2,…,λn組成的集合稱(chēng)為A的譜,其中n個(gè)特征值的模的最大值稱(chēng)為A的譜半徑,記為ρ(A).Perron-Frobenius定理中指出,對(duì)于n階不可約非負(fù)矩陣A,其譜半徑ρ(A)是A的特征值并且A有一個(gè)對(duì)應(yīng)于ρ(A)的正特征向量.

非負(fù)矩陣譜半徑的估計(jì)作為非負(fù)矩陣?yán)碚摰暮诵膯?wèn)題之一,許多學(xué)者都致力于這方面的研究.其中最有名且應(yīng)用最多的界值由Frobenius首先得到,即非負(fù)矩陣A的譜半徑的上下界分別為A的最大行(列)和與最小行(列)和.對(duì)于正矩陣A,Lederman,Ostrowski,Brauer對(duì)Frobenius界值又相繼作了改進(jìn).但對(duì)于最大行(列)和與最小行(列)和相差很大的矩陣,上述界值并不理想,因此需要更多更好的方法.

目前關(guān)于譜半徑的界已經(jīng)有許多深刻的結(jié)論,其中有如下的著名定理:

定理[1](Wielandt) 設(shè)A=(aij)是n階非負(fù)矩陣,其譜半徑為ρ(A),x是n維列正向量,那么

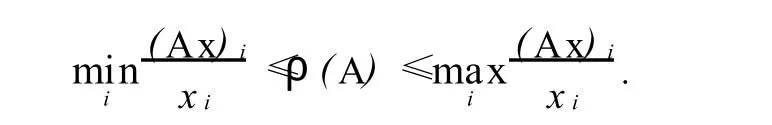
如果A不可約,那么等號(hào)成立當(dāng)且僅當(dāng)x是相應(yīng)于ρ(A)的特征向量.

本文將上述定理進(jìn)行了推廣,通過(guò)理論和數(shù)值例子的證明,可以顯示推廣后的方法所得到的結(jié)果精確度更高.

2 主要結(jié)論

引理1[2]設(shè)q1,…,qn是正數(shù),p1,…,pn是任意實(shí)數(shù),則

當(dāng)且僅當(dāng)所有的比值pi/qi相等時(shí),等號(hào)成立.

定理1 設(shè)A是n階不可約非負(fù)矩陣,x是n維列正向量,則對(duì)任意的m∈N+,有

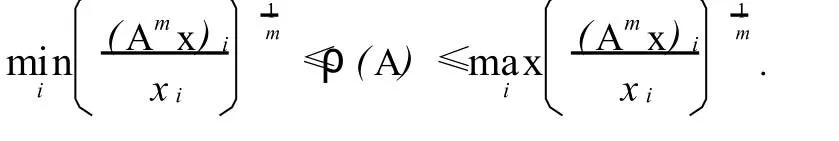
3 數(shù)值例子

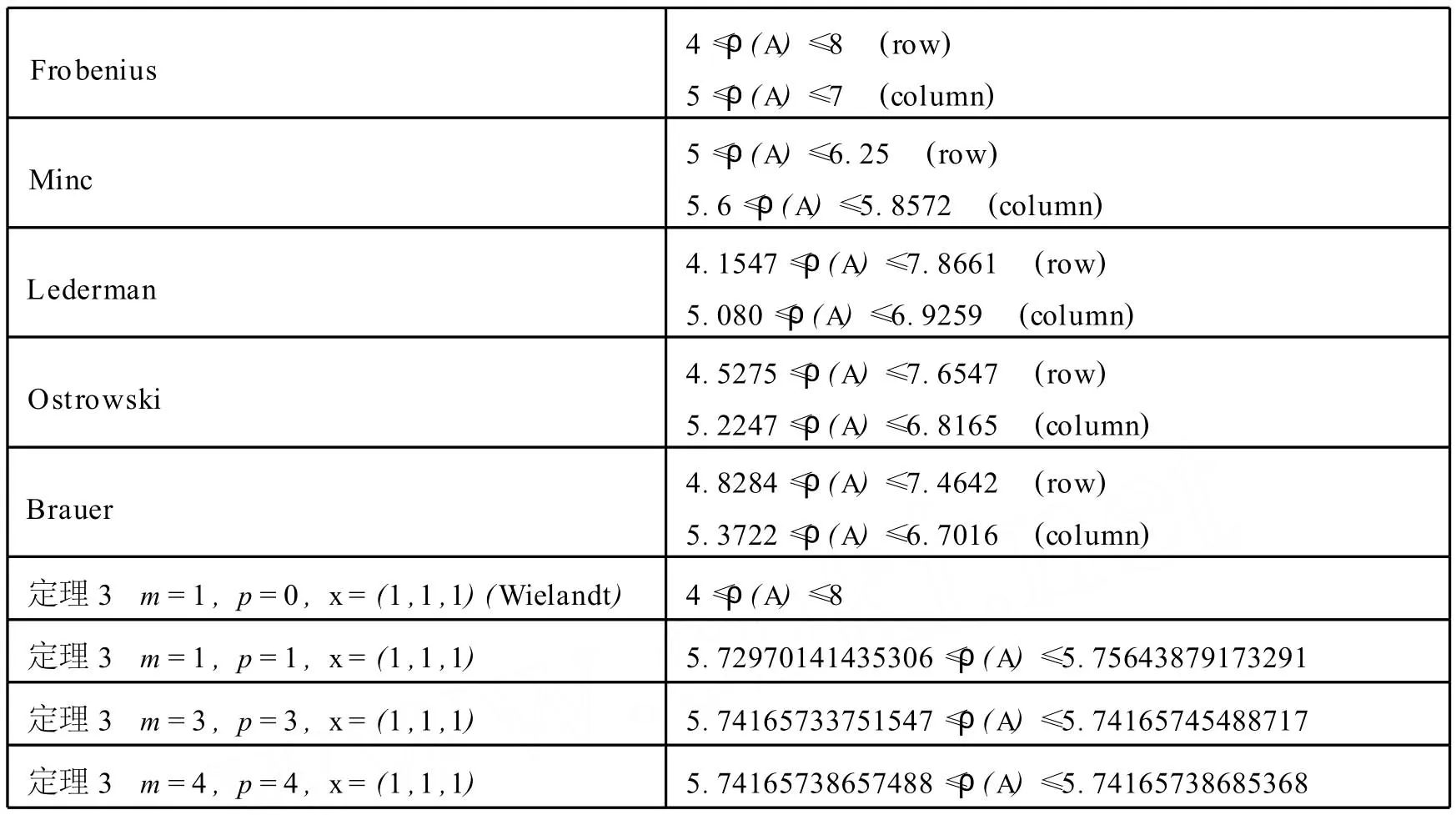
表1 各種界值比較

從上表可以看出,隨著m,p的增加,譜半徑界值更為精確.通過(guò)更為多的數(shù)值例子可以得出,界值關(guān)于p的收斂速度比關(guān)于m的收斂速度要快.但本文中并未給出證明.

注 求不可約非負(fù)矩陣譜半徑的任何方法都可用以計(jì)算一般非負(fù)矩陣的譜半徑,本文中的方法也不例外.事實(shí)上,對(duì)于任意的非負(fù)矩陣A(可約或不可約),都存在置換矩陣P使

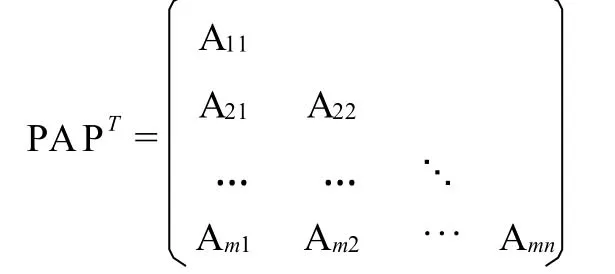
為下三角形分塊矩陣,其中Aii(i=1,…,m)都是不可約非負(fù)矩陣,而且ρ(A)=ρ(PAP)T=maxρ(Aii).

致謝 衷心感謝黃廷祝教授的指導(dǎo).

[1] Berman A and Plemmons R J.Nonnegative matrices in Mathematics Science[M].New York：Academic Press, 1979.

[2] Minc H.Nonnegative Matrices[M].New York：Wiley,1988.

[3] 黃廷祝,楊傳勝.特殊矩陣及應(yīng)用[M].北京：科學(xué)出版社,2007.

[4] 殷劍宏.求非負(fù)矩陣最大特征值與特征向量C-W方法[J].合肥工業(yè)大學(xué)學(xué)報(bào),2000,23(5)：752-756.

A New Bound for the Spectral Radius of a Nonnegative Matrix

L I Dan-qing
(School of Appl.Math.,Univ.of Electronic Science and Technology of China,Chengdu,Sichuan 611731,China)

Based on a theorem of Wielandt’s,a new estimate for the spectral radius of a nonnegative matrix is presented.A numerical example is provided to illustrate the effectiveness of this approach.

nonnegative matrix;spectral radius;bound

O151.21

A

1672-1454(2011)03-0026-04

2008-07-01;[修改日期]2009-04-02