陳益智,邵勇

(1.廣東惠州學(xué)院數(shù)學(xué)系,廣東惠州 516007;2.西北大學(xué)數(shù)學(xué)系,陜西西安 710127)

正規(guī)密碼H#-富足半群的結(jié)構(gòu)

陳益智1,2,邵勇2

(1.廣東惠州學(xué)院數(shù)學(xué)系,廣東惠州 516007;2.西北大學(xué)數(shù)學(xué)系,陜西西安 710127)

證明了H#-富足半群S是正規(guī)密碼H#-富足半群當(dāng)且僅當(dāng)它是完全J#-單半群的強(qiáng)半格.該結(jié)果也是正規(guī)密碼超富足半群和正規(guī)密碼群并半群分別在超富足半群和完全正則半群上的相應(yīng)結(jié)構(gòu)定理的推廣.

#-格林關(guān)系;正規(guī)密碼H#-富足半群;完全J#-單半群;強(qiáng)半格

1 引言

文[1-2]中,作者引入了格林?-關(guān)系.它的等價(jià)表述如下[3]:設(shè)S是半群

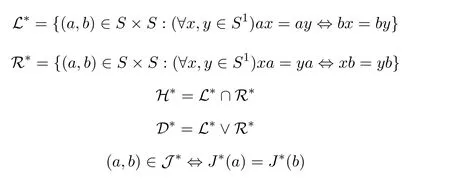
其中,J?(a)和J?(b)分別是由a和b生成的主?-理想.

文[3]中,作者研究了富足半群,這類半群的每個(gè)L?-類和每個(gè)R?-類都包含了至少一個(gè)冪等元.此外,作者還給出了超富足半群的概念,即每個(gè)H?-類都包含有一冪等元的半群稱為是超富足半群.容易看出,富足半群、超富足半群分別是正則半群和完全正則半群的真推廣.此外,文[4]中系統(tǒng)地研究了超富足半群的結(jié)構(gòu),推廣了文[5]中的關(guān)于完全正則半群結(jié)構(gòu)的相應(yīng)結(jié)果,并完善了文[3]中關(guān)于超富足半群的相關(guān)結(jié)論.

由文[3]知道,如果半群S的每個(gè)冪等元都是本原的,那么S就被稱為是本原的;如果富足半群S是本原的,并且S的冪等元生成一個(gè)正則子半群,則S稱為是完全J?-單半群;S是完全J?-單半群也等價(jià)于S是超富足半群并且是J?-單的.顯然,完全J?-單半群是由Clifford和Petrich在文[6]所研究的完全單半群的推廣.

最近,文[7]定義了一類新的格林關(guān)系:#-格林關(guān)系.即

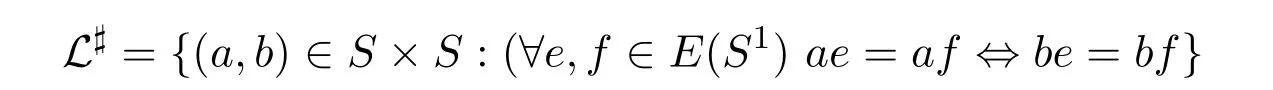
由文[8]可知,超富足半群S是正規(guī)密碼超富足半群當(dāng)且僅當(dāng)它是完全J?-單半群的強(qiáng)半格.同時(shí),注意到H#-富足半群是超富足半群的推廣,完全J#-單半群是完全J?-單半群的推廣,于是,自然地我們會(huì)考慮這樣的問題:正規(guī)密碼H#-富足半群是否與完全J#-單半群的強(qiáng)半格等價(jià)?

本文就上面提出的問題進(jìn)行了研究探討,且證明給出:半群S是正規(guī)密碼H#-富足半群當(dāng)且僅當(dāng)它是完全J#-單半群的強(qiáng)半格.該結(jié)果也是正規(guī)密碼超富足半群和正規(guī)密碼半群在超富足半群和完全正則半群上的相應(yīng)結(jié)構(gòu)定理的推廣.

為了給出本文主要結(jié)果,首先引進(jìn)了#-富足半群上的自然偏序,然后探討了H#-富足半群的若干性質(zhì)和特征,最后證明了正規(guī)密碼H#-富足半群的主要結(jié)構(gòu)定理,同時(shí)還對(duì)其兩類特殊情形進(jìn)行了探討.

對(duì)于本文未提及的概念和術(shù)語,讀者可參看文[7,9-11].

2 #-富足半群上的自然偏序

本節(jié)將主要引進(jìn)#-富足半群上的自然偏序的概念.

證明我們只需證L#(xa)?L#(a)即可.顯然,xa∈S1a,其中S1a是包含a的最小左理想.由于L#(a)是一個(gè)包含a的左理想,故有S1a?L#(a),從而xa∈L#(a).另一方面,因?yàn)長(zhǎng)#(xa)是包含xa的最小左#-理想,并且L#(a)也是左#-理想,于是,L#(xa)?L#(a).

特別地,對(duì)于半群S的正則元素來說,上述所定義的偏序剛好就是文[12]所研究的正則元素偏序的情形.

類似地,可以證明≤r也是偏序.另外,直接驗(yàn)證可知,當(dāng)≤l和≤r限定在E(S)時(shí)剛好就是ω.

現(xiàn)在,定義#-富足半群上的自然偏序?yàn)椤?≤l∩≤r.容易看出,我們所定義的偏序正是正則或富足半群上的自然偏序的的一個(gè)推廣[12-13].

3 主要結(jié)果

引理3[7]設(shè)S是H#-富足半群,則H#是同余當(dāng)且僅當(dāng)對(duì)任意的a,b∈S,(ab)0=(a0b0)0.

引理4[7]密碼H#-富足半群S是完全J#-單半群Sα的半格Y,記為S=(Y,Sα).

命題2設(shè)S=(Y,Sα)是一個(gè)密碼H#-富足半群.則下列命題成立:

(1)若a∈Sα且α≥β,則存在b∈Sβ使得b≤a;

(2)若a,b,c∈S,bH#c且b,c≤a,則b=c;

(3)若a∈E(S),b∈S且有b≤a,則b∈E(S).

證明(1)令a∈Sα,b1∈Sβ.因?yàn)镠#是同余,且注意到aH#a0,有

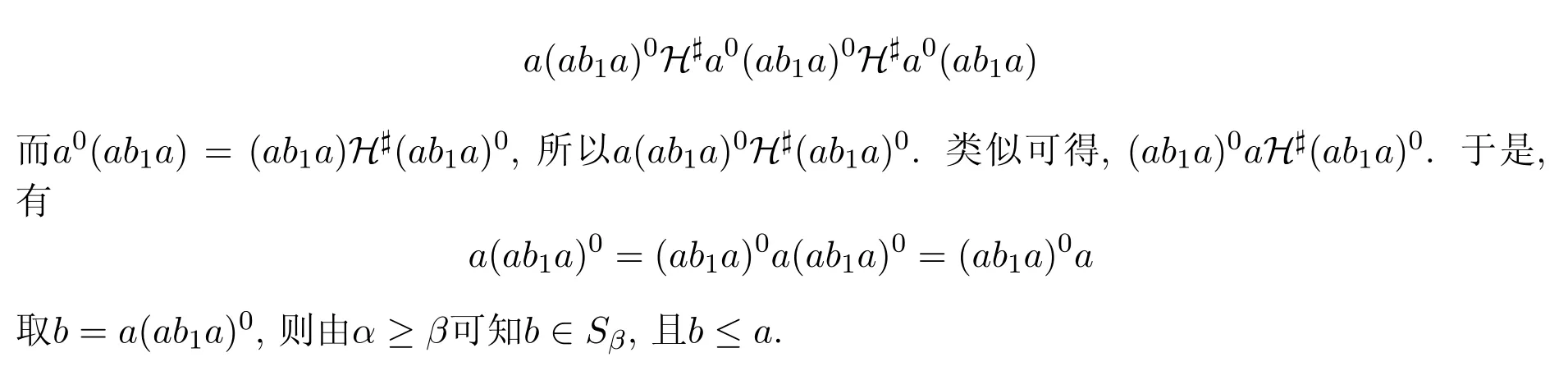
(2)若a,b,c∈S,b,c≤a,則存在e,f,g,h∈E(S)使得b=ea=af,c=ga=ah.因?yàn)镾是H#-富足半群,且注意到eb=b,bH#b0,從而有eb0=b0.類似地有c0h=c0.又bH#c,所以ec=ec0c=eb0c=b0c=c0c=c.類似可得bh=b.于是b=bh=eah=ec=c.

(3)若a,b∈S且b≤a,則存在e,f∈E(S)使得b=ea=af.又因?yàn)閍∈E(S),所以

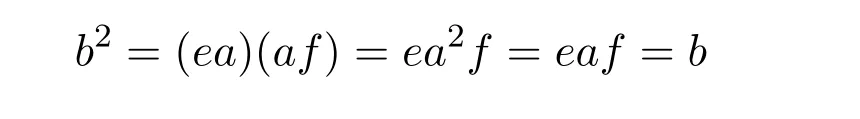
這即表明b∈E(S).

命題3設(shè)S=(Y,Sα)是正規(guī)密碼H#-富足半群,則下列命題成立:

(1)若a∈Sα,則對(duì)任意的α≥β,存在唯一的aβ∈Sβ使得aβ≤a;

(2)對(duì)于任意的α≥β,若對(duì)于a∈Sα,b∈Sβ,存在冪等元e∈Sα使得e≤a0,則有eab= ab,bae=ba,ea=ae以及(ea)0=e.

證明(1)由命題2的(1)及其證明過程可知,對(duì)任意c∈Sβ,存在b=a(aca)0=(aca)0a∈Sβ使得b≤a.下證這樣的b是唯一的.

現(xiàn)假定還存在b1∈Sβ,使得b1≤a,則此時(shí)存在g,h∈E(S),滿足b=ga=ah.因?yàn)镠#是同余,于是有

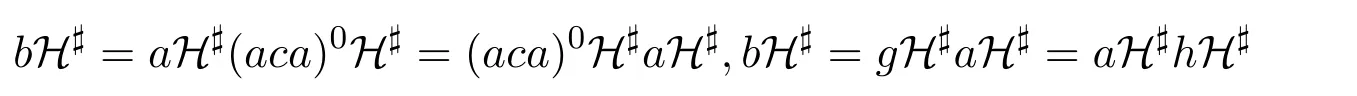
這即表明,bH#≤aH#,b1H#≤aH#.又因?yàn)?S/H#是正規(guī)帶,它可分解為矩形帶的(強(qiáng))半格,故有S/H#=(Y,Sα/H#),從而

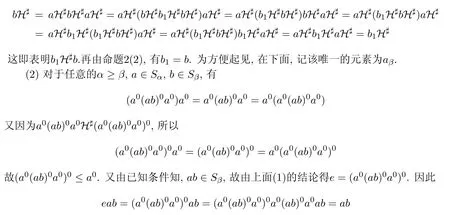
同理可得bae=ba.另外,因?yàn)樵撌绞菍?duì)任意的b∈Sβ都成立,所以可取b=e,此時(shí),有ae=ea,由引理3,即可得(ea)0=(ea0)0=e.

命題4設(shè)S是密碼完全J#-單半群,?a,b∈S,若b≤a,則有b=a.

證明?a,b∈S,若b≤a,則存在e,f∈E(S)使得b=ea=af.因?yàn)镾是H#-富足半群,且注意到eb=b,bf=b,從而有ba0=b=a0b.又bH#b0,所以a0b0=b0=b0a0,即b0≤a0.又因?yàn)镾是完全J#-單的,所以由引理4得a0=b0,即有aH#b.顯然a,b≤a,故由命題2(2)可得b=a.

命題5若?是密碼完全J#-單半群S到密碼完全J#-單半群T的同態(tài),則對(duì)于任意的a∈S有(a?)0=a0?.

證明首先,因?yàn)閍0?=(a0a0)?=(a0?)(a0?)=(a0?)2,所以a0?∈E(T).另外

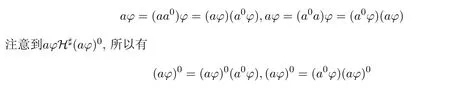
這即表明:(a?)0≤(a0?).又T是完全J#-單半群,由引理4可得(a?)0=(a0?).

從上面命題的證明過程可知,密碼完全J#-單半群之間的同態(tài)?其實(shí)是保持格林關(guān)系H#,L#, R#的,當(dāng)然格林關(guān)系D#也將被保持.

定理1H#-富足半群S是正規(guī)密碼H#-富足半群當(dāng)且僅當(dāng)它是完全J#-單半群的強(qiáng)半格.

證明(?)設(shè)半群S是S=(Y,Sα,?α,β)是完全J#-單半群Sα的強(qiáng)半格Y,下面證明S是正規(guī)密碼H#-富足半群.為此,只需證明H#是S上的同余及S/H#是個(gè)正規(guī)帶.

i)先證H#是S上的同余.對(duì)于任意的a∈Sα,b∈Sβ,有ab=a?α,αβb?β,αβ.注意到密碼完全J#-單半群間的同態(tài)保持相應(yīng)的格林關(guān)系,再由命題5,有

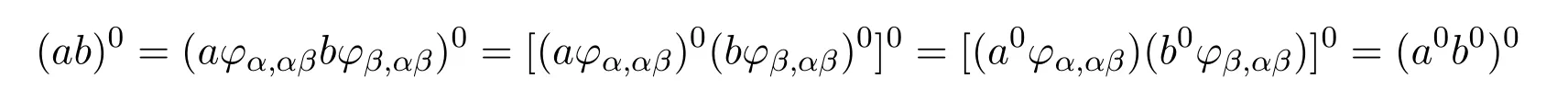
于是,由引理3,H#是同余.

ii)再證S/H#是個(gè)正規(guī)帶.首先,由于H#是同余,則S/H#是個(gè)帶,并且此時(shí)Sα/H#是矩形帶.設(shè)a∈Sα,b∈Sβ,c∈Sγ,并令δ=αβγ.于是

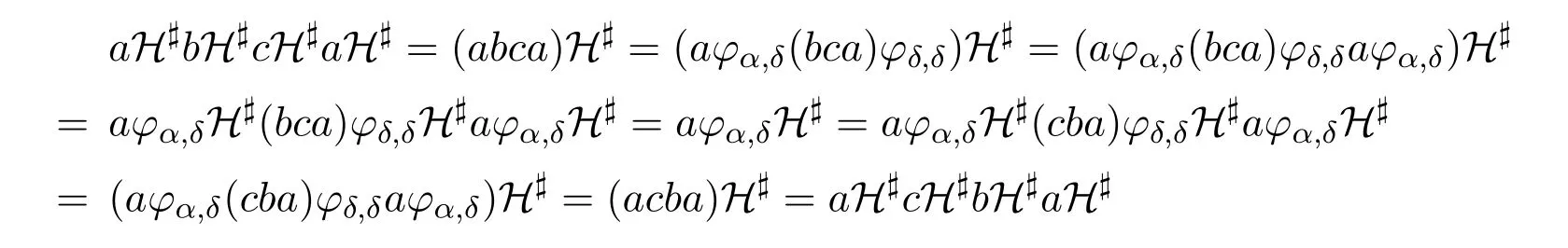
這即表明S/H#是個(gè)正規(guī)帶.

(?)設(shè)半群S是正規(guī)密碼H#-富足半群,由引理4,有S=(Y,Sα),其中Y為半格,并且對(duì)于任意的α∈Y,Sα為完全J#-單半群.對(duì)于α≥β及任意的a∈Sα,定義映射?α,β:Sα→Sβ,a 7→aβ,其中aβ是在命題3中使得aβ≤a成立的Sβ中的唯一的元素,并且對(duì)任意的c∈Sβ,有

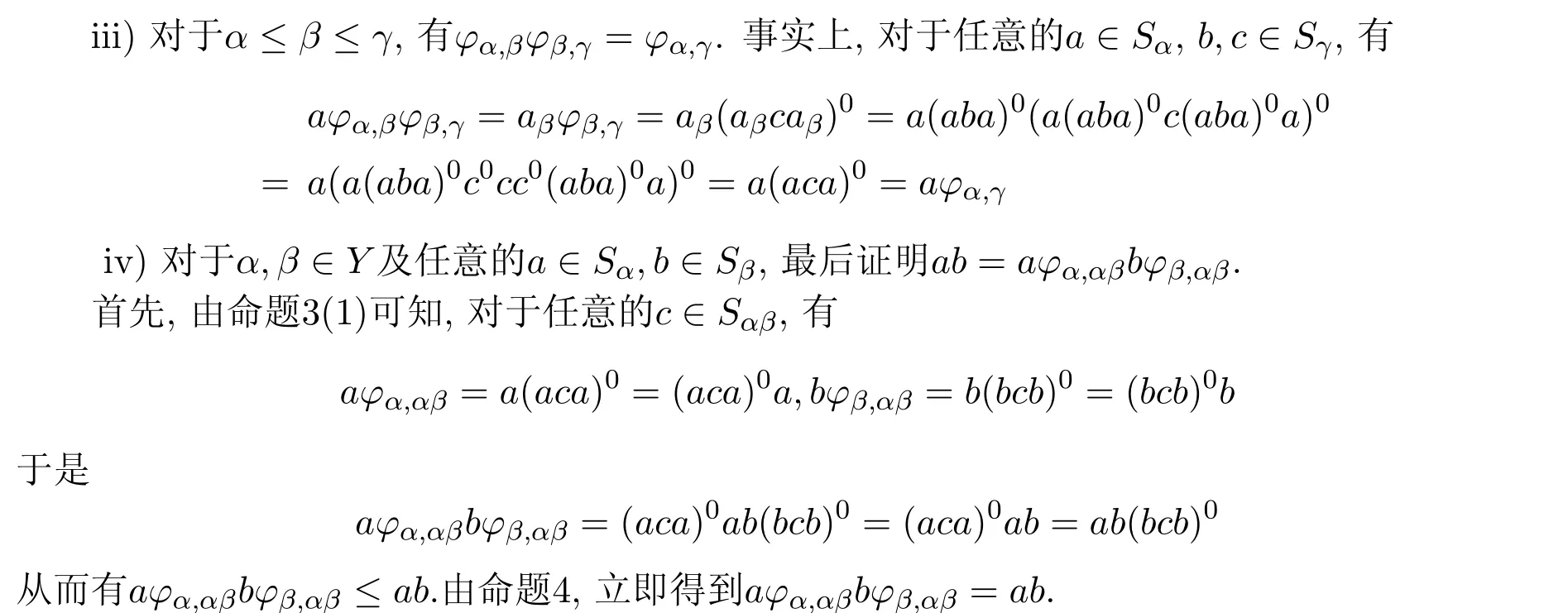
綜上,證明了S=(Y,Sα,?α,β)是完全J#-單半群Sα的強(qiáng)半格.

注意到H#-富足半群是超富足半群的推廣,于是在定理1中,如果把H#-富足半群限定在超富足半群上討論,則此時(shí)正規(guī)密碼H#-富足半群剛好就是正規(guī)密碼超富足半群,完全J#-單半群正好就是完全J?-單半群.于是,得到文[8]中的定理4.3,即為下面的推論:

推論1超富足半群S是正規(guī)密碼超富足半群當(dāng)且僅當(dāng)它是完全J?-單半群的強(qiáng)半格.

此外,在定理1中,如果我們把H#-富足半群再限定在完全正則半群上考慮,則此時(shí)正規(guī)密碼H#-富足半群剛好就是正規(guī)密碼群并半群,完全J#-單半群也正好就是完全單半群.同樣地,可以得到如下推論

推論2完全正則半群S是正規(guī)密碼群并半群當(dāng)且僅當(dāng)它是完全單半群的強(qiáng)半格.

[1]Mcalister D B.One-to-one partial right translations of a right cancellative semigroup[J].J.Algebra,1976,43:231-251.

[2]Pastijn F.A representation of a semigroup by a semigroup of matrices over a group with zero[J].Semigroup Forum,1975,10:238-249.

[3]Fountain J B.Abundant semigroups[J].Proc.London Math.Soc.,1982,44(3):103-129.

[4]Ren X M,Shum K P.The structure of superabundant semigroups[J].Science in China,Ser.A,Math., 2004,47(5):756-771.

[5]Petrich M.The structure of completely regular semigroups[J].Trans.Amer.Math.Soc.,1974,189:211-236.

[6]Clifford A H,Petrich M.Some classes of completely regular semigroups[J].J.Algebra,1977,46:462-480.

[7]丁月,孔祥智.H#-富足半群[J].山東大學(xué)學(xué)報(bào):理學(xué)版,2008,43(4):55-61.

[8]Kong X Z,Shum K P.On the structure of regular crypto semigroups[J].Comm.Algebra,2001,29(6):2461-2479.

[9]Howie J M.An Introduction to Semigroup Theory[M].London:Academic Press,1976.

[10]Howie J M.Fundamentals of Semigroup Theory[M].Oxford:Clarendon Press,1995.

[11]潘秀娟,邵勇,田俊華.乘法半群為正規(guī)純整群的半環(huán)[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2005,21(1):76-79.

[12]Nambooripad K S S.The natural partial order on a regular semigroup[J].Proc.Edinburgh Math.Soc., 1980,23:249-260.

[13]Lawson M V.The natural partial order on an abundant semigroup[J].Proc.Edinburgh Math.Soc., 1987,30:169-186.

A construction of normal crypto H#-abundant semigroups

CHEN Yi-zhi1,2,SHAO Yong2

(1.Department of Mathematics,Huizhou University,Huizhou516007,China; 2.Department of Mathematics,Northwest University,Xi’an710127,China)

In this paper,a new construction theorem of normal crypto H#-abundant semigroups is given,i.e., an H#-abundant semigroup is a normal crypto H#-abundant semigroup if and only if it is a strong semilattice of completely J#-simple semigroups.Actually,the main result in this paper is a generalization of the corresponding ones of normal crypto semigroups and normal cryptogroups in superabundant and completely regular semigroups respectively.

Green’s#-relations,normal crypto H#-abundant semigroups,completely J#-simple semigroups, strong semilattice

O152.7

A

1008-5513(2009)04-0794-07

2008-11-10.

廣東省自然科學(xué)基金(8151601501000002,9151051501000066),廣東惠州學(xué)院校立基金(C208·0403,A08002).

陳益智(1980-),博士,講師,研究方向：代數(shù)學(xué).

2000MSC:20M10