徐洪焱,易才鳳

(1.景德鎮(zhèn)陶瓷學(xué)院信息學(xué)院,江西景德鎮(zhèn) 333403;2.江西師范大學(xué)數(shù)信學(xué)院,江西南昌 330027)

亞純函數(shù)及其n階導(dǎo)數(shù)權(quán)分擔(dān)兩個值

徐洪焱1,易才鳳2

(1.景德鎮(zhèn)陶瓷學(xué)院信息學(xué)院,江西景德鎮(zhèn) 333403;2.江西師范大學(xué)數(shù)信學(xué)院,江西南昌 330027)

研究亞純函數(shù)及其n階導(dǎo)數(shù)權(quán)分擔(dān)兩個值的唯一性問題.得到了:如果兩個非常數(shù)亞純函數(shù)f,g分擔(dān)(∞,∞),f(n)與g(n)分擔(dān)(1,0),n(≥0)為一整數(shù),且滿足△C0:= (4n+6)λ+δn+1(0,f)+δn+1(0,g)+δn+2(0,f)+δn+2(0,g)+δn(0,f)＞4n+10,其中λ=max{min{Θ(∞,f),Θ(0,f)},min{Θ(∞,g),Θ(0,g)}},那么f(n)·g(n)≡1,或者f≡g.該結(jié)果改進(jìn)了前人的有關(guān)定理.

亞純函數(shù);權(quán)分擔(dān);唯一性

1 引言及主要結(jié)果

2 引理

3 定理1.1的證明

這樣很容易知道H的極點(diǎn)只可能發(fā)生以下幾種情況:(1)F,G的重級零點(diǎn);(2)F,G的重級極點(diǎn);(3)F,G的1-值點(diǎn)且其重數(shù)不相等;(4)F'的零點(diǎn)但非F(F?1)的零點(diǎn);(5)G'的零點(diǎn)但非G(G?1)的零點(diǎn).

(i)由(i)的條件,知F,G分擔(dān)(1,0),(∞,∞),再根據(jù)H的表達(dá)式很容易知道F,G的極點(diǎn)不是H的極點(diǎn).

如果H/≡0,由引理2.7,有

類似于情形1也可得到矛盾.

如果a?1=0,則f(n)≡g(n).由此方程可得到f=g+p(z),這里p(z)為多項(xiàng)式,顯然T(r,f)=T(r,g)+S(r,f).如果p(z)/≡0,根據(jù)引理2.2,有

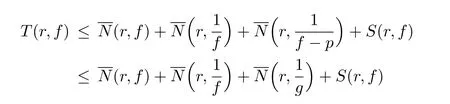
由(1.1)式很容易得到T(r,f)≤S(r,f),r∈I矛盾.因此p(z)≡0,即f≡g.

綜合三種情形,定理1.1(i)得證.下證定理1.1(ii).

(ii)因?yàn)閒(n)與g(n)分擔(dān)(1,0),所以F,G分擔(dān)(1,0).

如果H/≡0,則(3.1)式變?yōu)?/p>

4 定理1.2的證明

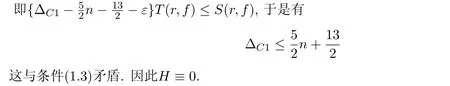
如果H≡0,類似于定理1.1可以證得f(n)·g(n)≡1,或者f≡g,即定理1.2(i)得證.

類似于定理1.1(ii)證明方法并結(jié)合(4.1)-(4.4)式及f,g分擔(dān)(∞,0),也很容易證明.這里略之.

綜上所述,則完成了定理1.2的證明.

[1]Hayman W K.Meromorphic Functions[M].Oxford:Clarendon Press,1964.

[2]Yi H X,Yang C C.Uniqueness Theory of Meromorphic Functions[M].Beijing:Science Press,1995.

[3]Yang C C.On two entire functions which together with their first derivatives have the same zeros[J].J.Math. Anal.Appl.,1976,56:1-6.

[4]Yi H X.A question of C C Yang on uniqueness of entire functions[J].Kodai Math.J.,1990,13:39-46.

[5]Yuan W J,Tian H G.Further results of some uniqueness theorems for meromorphic functions whose n-th derivatives share the same 1-points[J].Advances in Applied Clifford Algebras,2001,11(S2):317-325.

[6]Lahiri I.Weighted sharing and uniqueness of meromorphic functions[J].Nagoya Math.J.,2001,161:193-206.

[7]Lahiri I.On a result of Ozawa concerning uniqueness of meromorphic functions I[J].J.Math.Anal.Appl., 2003,283:66-76.

[8]Banerjee A.Weighted sharing of a small function by a meromorphic function and its derivative[J].Comput. Math.Appl.,2007,53:1750-1761.

[9]Banerjee A.Meromorphic functions sharing one value[J].Int.J.Math.Math.Sci.,2005,22:3587-3598.

[10]Lahiri I.Weighted value sharing and uniqueness of meromorphic functions[J].Complex Variables Theory Appl.,2001,46(3):241-253.

[11]Zhang Q C.Meromorphic function that shares one small function with its derivative[J].J.Inequal.Pure Appl.Math.,2005,6(4):Article 116,13pp.http://jipam.vn.edu.au/.

Mermorphic functions concerning their n-th derivative sharing two values with weight

XU Hong-yan1,YI Cai-feng2

(1.Department of Informatics and Engineering,Jingdezhen Ceramic Institute,Jingdezhen333403,China; 2.Institute of Mathematics and Informatics,Jiangxi Normal University,Nanchang330027,China)

In this paper,we deal with the uniqueness problem of meromorphic functions concerning their n-th derivative sharing two values with weight and obtain the following theorem:if two nonconstant meromorphic functions f,g share(∞,∞),fn,gnshare(1,0),and satisfy△C0:=(4n+6)λ+δn+1(0,f)+δn+1(0,g)+δn+2(0,f)+ δn+2(0,g)＞4n+10,where λ=max{min{Θ(∞,f),Θ(0,f)},min{Θ(∞,g),Θ(0,g)}},then either f(n)·g(n)≡1 or f≡g,where n(＞0)is an integer.These results extend the former theorems.

meromorphic function,weighted sharing,uniqueness

O174.52

A

1008-5513(2009)04-0777-09

2008-04-21.

國家自然科學(xué)基金(10871108),景德鎮(zhèn)陶瓷學(xué)院科研項(xiàng)目(景陶院發(fā)[2009]86號).

徐洪焱(1980-),碩士,研究方向：復(fù)分析.

2000MSC:30D30,30D35