王寶勤,周小輝,趙曉華,袁麗霞

(1.新疆師范大學(xué)數(shù)理信息學(xué)院,新疆烏魯木齊 830054; 2.浙江師范大學(xué)數(shù)理信息工程學(xué)院,浙江金華 321004)

Leibniz代數(shù)胚上動力系統(tǒng)的軌道范例與圖示

王寶勤1,周小輝1,趙曉華2,袁麗霞1

(1.新疆師范大學(xué)數(shù)理信息學(xué)院,新疆烏魯木齊 830054; 2.浙江師范大學(xué)數(shù)理信息工程學(xué)院,浙江金華 321004)

首先陳述Leibniz代數(shù)胚上的動力系統(tǒng)和在局部坐標(biāo)系下該動力系統(tǒng)的方程,在此基礎(chǔ)上,給出了動力系統(tǒng)軌道的范例和圖示.

向量叢;Leibniz代數(shù)胚;動力系統(tǒng)的軌道

1 引言

人們曾把經(jīng)典的Poisson括號和經(jīng)典Hamilton系統(tǒng)推廣為廣義Poisson括號和廣義Hamilton系統(tǒng),正是這種推廣使具有Hamilton形式的動力系統(tǒng)具有了很多特殊的動力學(xué)性質(zhì),但是這種推廣系統(tǒng)和括號,只能描述保守力學(xué)系統(tǒng),對耗散系統(tǒng)等是不能用Poisson括號描述的.由于許多領(lǐng)域不斷提出的實際問題和眾多學(xué)科發(fā)展的需要,很有必要對前述理論做進(jìn)一步的推廣[12].過去二十年來,學(xué)者們對這種推廣的努力不斷在進(jìn)行,特別值得一提的是,推廣系統(tǒng)的思想和方法相似于過去對廣義Hamilton系統(tǒng)的做法,即用一個括號結(jié)構(gòu),但括號結(jié)構(gòu)不是Poisson括號,而是Leibniz括號,Leibniz系統(tǒng)就是適合于某些耗散系統(tǒng)的動力學(xué)模型,還有許多重要的系統(tǒng)都能用Leibniz括號定義[3](如梯度系統(tǒng)和非完整約束簡單力學(xué)系統(tǒng)等).這種推廣的思想和趨勢還在不斷發(fā)展和深入,涉及到相應(yīng)的幾何描述層次也在提高,如所討論的動力系統(tǒng)涉及叢結(jié)構(gòu),李代數(shù)胚和Leibniz代數(shù)胚等[45],為了更好理解和深入研究這些動力系統(tǒng),我們在陳述理論的基礎(chǔ)上給出了范例和軌道的圖示.

2 Leibniz代數(shù)胚上的動力系統(tǒng)

賦予一個Leibniz代數(shù)胚結(jié)構(gòu)的向量叢π1:B→M叫做M上的Leibniz代數(shù)胚,并記作(B,[·,·],ρ1,ρ2).

如果Leibniz代數(shù)胚的括號[·,·]是反稱的(這種情形有ρ1=ρ2),它就叫做準(zhǔn)李代數(shù)胚(Pre-Lie algebroid).而若Leibniz代數(shù)胚的括號[·,·]是對稱的,它就叫做對稱代數(shù)胚(這種情形有ρ1=?ρ2).

對于一個給定的σ∈P,用下邊的關(guān)系式定義對偶叢空間B?上一個函數(shù)FB?σ

其中〈·,·〉是叢空間B和對偶叢空間之間的標(biāo)準(zhǔn)配對.

令Λ0是B?上一個2-逆變張量場,并對任意兩個函數(shù)f,g∈C∞(B?)定義括號[·,·]Λ0為

如果對P中每一對截面(σ1.σ2),定義在B?上的函數(shù)Λ0(dFB?σ1,dFB?σ2)是線性的,我們就說Λ0是線性的.

引理[4]對于每一個具有括號[·,·]和錨映射ρ1,ρ2的向量叢π1:B→M上的Leibniz代數(shù)胚結(jié)構(gòu),存在一個唯一的B?上的2-逆變張量場Λ0,使得下述關(guān)系式成立

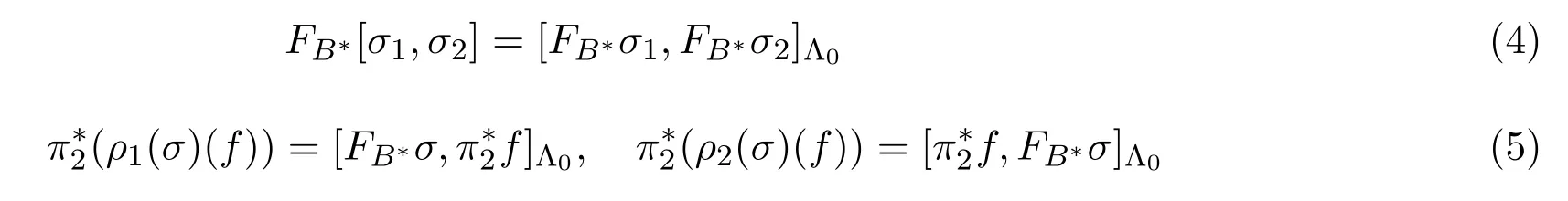
對所有σ,σ1,σ2∈P和f∈C∞(M).

反之,每一個B?上的2-逆變線性張量場Λ0,用關(guān)系式(4),(5)定義一個B上的Leibniz代數(shù)胚.這個引理表明:在向量叢π1:B→M上的Leibniz代數(shù)胚結(jié)構(gòu)和對偶向量叢π2:B?→M的叢流形B?上的2-逆變張量場之間建立起對應(yīng).

設(shè)dim M=n,dim B=m,{xi},i=1,···,n是M上的一個局部坐標(biāo)系;再設(shè){ej},j= 1,···,m是B的局部截面的一個基,而{ej},j=1,···,m表示B?的局部截面對偶基;(xi,ya)和(xi,ξa)依次分別表示B和B?上的坐標(biāo)系.

易知,每一個B?上的線性2-逆變張量場Λ0有如下形式

給出的相伴于向量場Xh的動力系統(tǒng),叫做Leibniz代數(shù)胚π1:B→M上的動力系統(tǒng).

3 范例和軌道圖示

設(shè)向量叢π1:B=R3×R3→R3,其對偶叢π2:B?=R3×(R3)?→R3.

下邊對每一個例子的敘述步驟是:

(1)先給出對偶叢B?上的2-逆變線性張量場Λ,兩個錨映射ρ1,ρ2的三階方陣表示以及函數(shù)h的表達(dá)式.

(2)根據(jù)已知的Λ,ρ1,ρ2,h,寫出相伴于Leibniz代數(shù)胚(R3×R3,Λ,ρ1,ρ2)的動力系統(tǒng)方程(9)和(10)的具體表達(dá)式.

(3)在一定條件下,給出動力系統(tǒng)在坐標(biāo)系Ox1x2x3和Oξ1ξ2ξ3中的軌道圖示.

取sinξ2=0.5,sinξ3=0.8;初值x1(0)=0.5,x2(0)=0.5,x3(0)=0.5

圖1 例1的軌道圖示圖

圖2 例2的軌道圖示

n=2,5時的兩組圖如下:

圖3 例3的軌道圖示1

n=7,8時的兩組圖如下:

圖4 例3的軌道圖示2

圖5 例4的軌道圖示

圖6 例5的軌道圖示

[1]王寶勤,袁麗霞,趙曉華.關(guān)于李群胚和泊松作用的討論[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2007,(23)4:487-492.

[2]袁麗霞,王寶勤.相配群胚上的誘導(dǎo)聯(lián)絡(luò)[J].數(shù)學(xué)進(jìn)展,2008(5):617-624.

[3]王寶勤,張福娥,趙曉華.關(guān)于L流形的一些討論[J].數(shù)學(xué)進(jìn)展,2009(3):359-366.

[4]Grabowski J,Urbanski P.Lie algebroids and Poisson-Nijenhuis structures[J].Rep.Math.Phys.,1997,40:195-208.

[5]Ortega J P,Planas-Bielsa V.Dynamics on Leibniz manifolds[J].Journal of Geometry and Physics,2004,52:1-27.

Example and graphical representation of orbits of dynamical systems on Leibniz algebroids

WANG Bao-qin1,ZHOU Xiao-hui1,ZHAO Xiao-hua2, YUAN Li-xia1

(1.School of Maths-Physics and Information Science,Xinjiang Normal University,Urmuqi830054,China; 2.School of Maths-Physics,Information and Engineering Science,Zhejiang Normal University, Jinhua321004,China)

First of all,we explain dynamical systems on Leibniz algebroids and equations of this dynamical systems in a system of local coordinates.On the base of this,example and graphical representation of orbits of dynamical system are given.

vector bundle,Leibniz algebroid,orbit of the dynamical system

O186.1

A

1008-5513(2009)04-0642-07

2008-11-10.

國家自然科學(xué)基金(10872183),新疆師范大學(xué)優(yōu)秀青年教師科研啟動基金(XJNU0728).

王寶勤(1937-),教授,研究方向：現(xiàn)代微分幾何及其應(yīng)用.

2000MSC:53C12