Convergence Rate of Estimator for Nonparametric Regression Model under-mixing Errors
(School of Mathematical Sciences,Anhui University,Hefei 230601,China)
§1.Introduction
Let{Xn,n≥1}be a random variable sequence defined on a fixed probability space(?,F,P).Write FS=σ(Xi,i∈S?N).Givenσ-algebras B,R in F,let
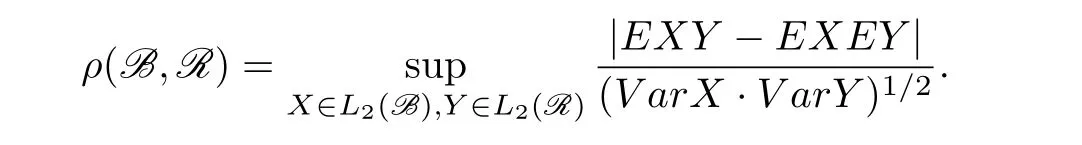
De fine the
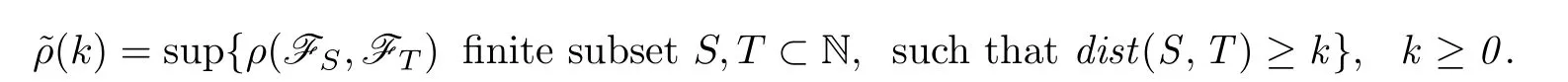
Definition 1.1A sequence of random variables{Xn,n≥1}is said to be a-mixing sequence if there existsk∈N such that(k)<1.
Recently,Wang et al[20]studied the nonparametric regression model based on-mixing errors and obtained the complete consistency of the estimator of unknown functiong(x).In this paper,we also investigate this nonparametric regression model and give the convergence rate for the estimator of unknown functiong(x).
Consider a fixed design regression model
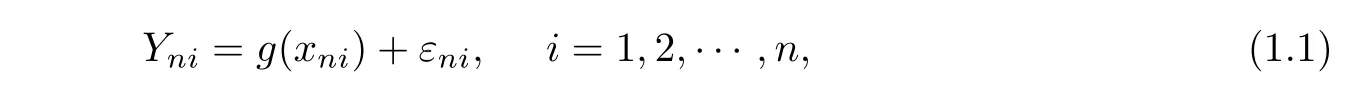
wherexniare design points on a setAinRqfor someq≥1,g(·)is an unknown function onAandεniare random errors.Assume that for eachn,(εn1,···,εnn)has the same distribution as(ε1,···,εn).As an estimator ofg(·),the following weighted regression estimator is given:
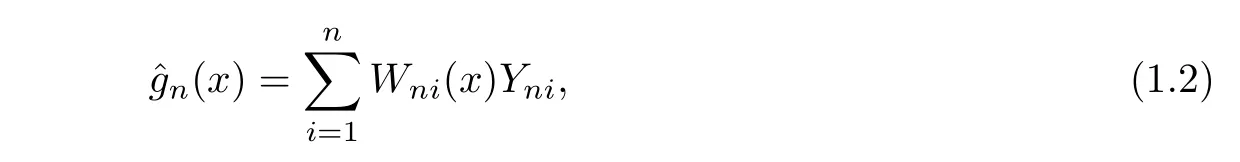
whereWni(x)=Wni(x;xn1,···,xnn)are weighted functions.
The estimators of nonparametric regression model such as weighted regression estimator has been studied by many authors.For example,under the independent errors,Georgiev and Greblicki[21],Müller[22]and Georgiev[23]studied the consistency and asymptotic normality for the estimator.Many authors extended the results of estimator ofg(x)to the dependent cases,for example,Roussas et al[24]for strong mixing errors,Tran et al[25],Hu et al[26]and Hu et al[27]for the linear time series,Liang and Jing[28]for the negatively associated(NA)errors,Yang et al[29]and Peng et al[30]for the negatively orthant dependent(NOD)errors,etc.
Recall that the sequence{Xn,n≥1}is stochastically dominated by a nonnegative random variableXif
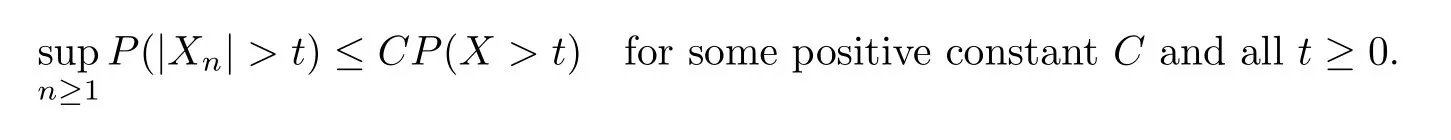
The method of stochastically dominated by a nonnegative random variable can be seen in many papers such as Adler and Rosalsky[31],Adler et al[32],Wu[33],etc.Hanson and Wright[34]and Wright[35]obtained a bound on tail probabilities for quadratic forms in the independent random variables by using the following condition.There existC>0 andγ>0 such that for alln≥1 and allx≥0,we haveP(|Xn|≥x)≤CHere,we can see it to be a formerly method of stochastically dominated by a nonnegative random variable.
In this paper,we investigate the nonparametric regression model(1.1)based on-mixing errors,which are stochastically dominated by a nonnegative random variable.We obtain the convergence rate for the weighted estimator of unknown functiong(x)inpth-mean,which implies the convergence rate in probability.Moreover,an example of the nearest neighbor estimator is illustrated and convergence rates of estimator are presented.For the details,please see our Theorem 2.1 and Example 2.1 in Section 2.
Under the nonparametric regression model of(1.1),for any fixed pointx∈AinRq(q≥1)and somep≥1,we list some assumptions on weighted functionWni(x)=Wni(x;xn1,···,xnn)as follows:
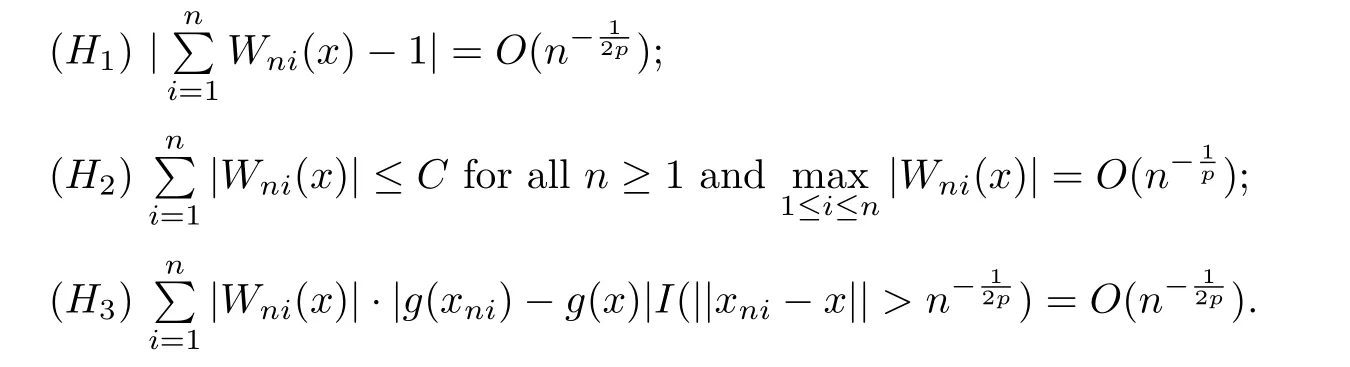
Lemma 1.1[5]For a positive integern0≥1 and positive real numbersp≥2 and 0≤r<1,there is a positive constantC=C(p,n0,r)such that if{Xn,n≥1}is a sequence of-mixing random variables with≤r,EXn=0 andE|Xn|p<∞for everyn≥1,then for alln≥1
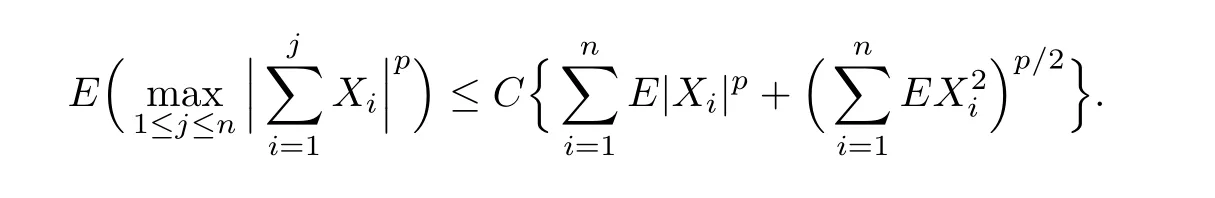
Lemma 1.2[31?33]Let{Xn,n≥1}be a sequence of random variables,which is stochastically dominated by a nonnegative random variableX.Then,for anyα>0 andb>0,the following two statements hold:
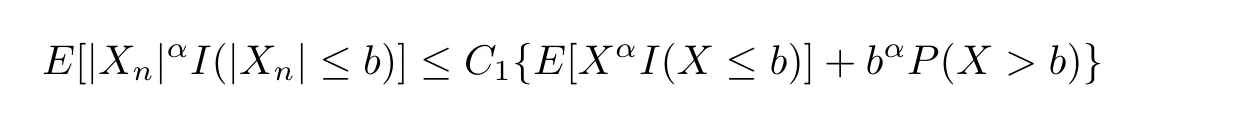
and
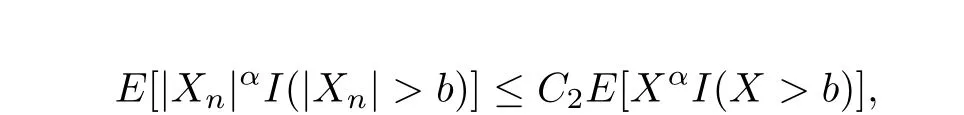
whereC1andC2are positive constants.Consequently,it hasE|Xn|α≤C3EXαfor alln≥1,whereC3is a positive constant.
§2.The Main Result and Its Proofs
First,we study the convergence rate of the estimator(1.2)forg(x)inpth-mean,which implies the convergence rate in probability.
Theorem 2.1Let{εn,n≥1}be a mean zeromixing sequence withn0≥1,0≤r<1 and≤r.Assume that the sequence of{εn,n≥1}is stochastically dominated by a nonnegative random variableZwithEZ2p<∞for somep≥1.Suppose that the conditions(H1)-(H3)hold true andg(x)satis fies a local Lipschitz condition around the pointx∈A.Then it has
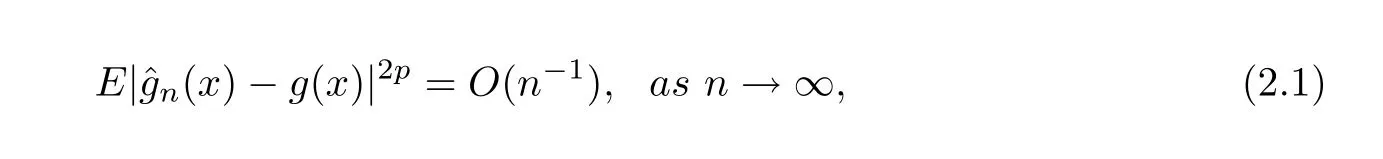
which implies
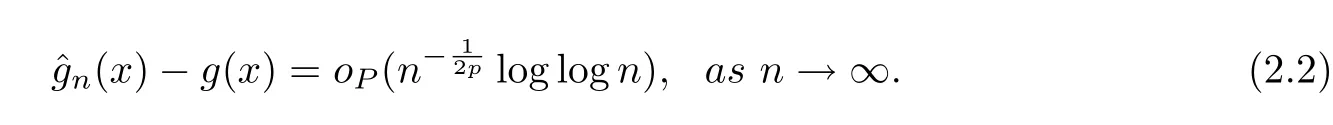

Let 1≤kn≤n,the nearest neighbor weight function estimator ofg(x)in model(1.1)is defined as follows:
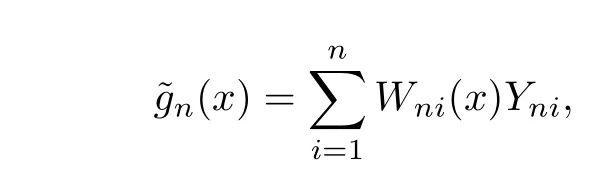
where
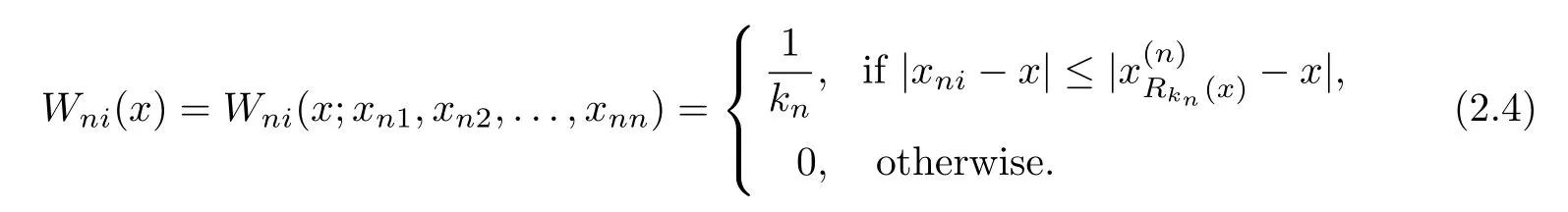
So,for everyx∈[0,1],by de finition ofRi(x)and choice ofxniandkn=[n1/2],it follows
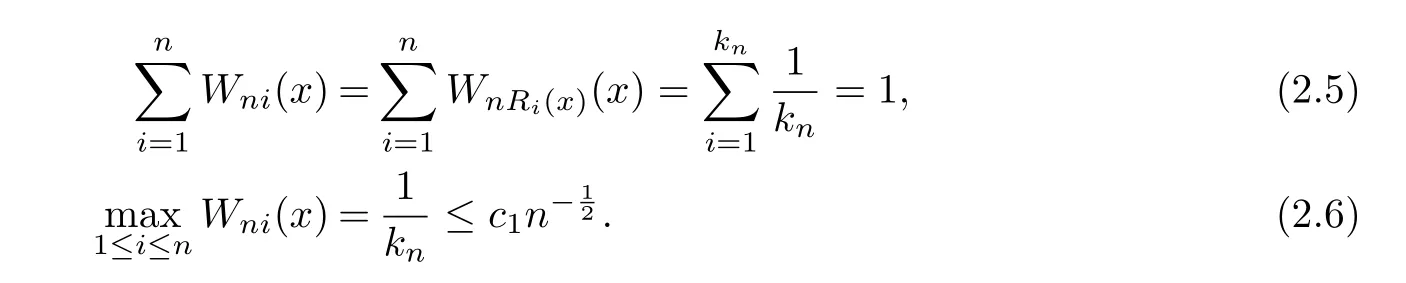
Meanwhile,it is easy to check that
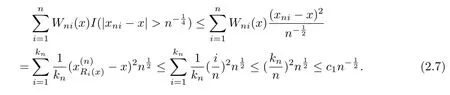
In addition,We assume thatg(x)satis fies a local Lipschitz condition around the pointx∈[0,1].So by(2.4)-(2.7),it can be found that the assumptions of(H1)-(H3)withp=2 are satis fied.Consequently,we make use of Theorem 2.1 and obtain that
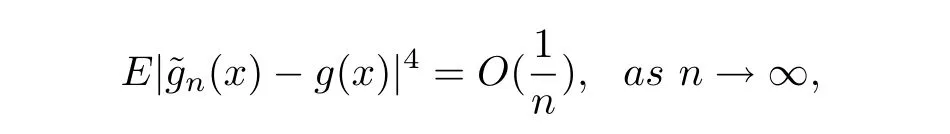
which yields
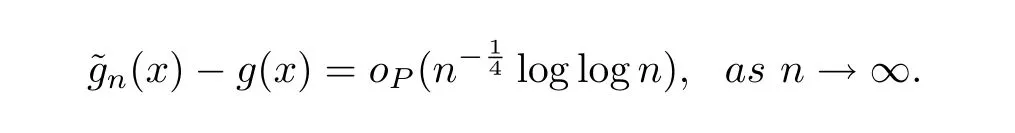
Proof of Theorem 2.1On the one hand,forx∈A,it can be seen that
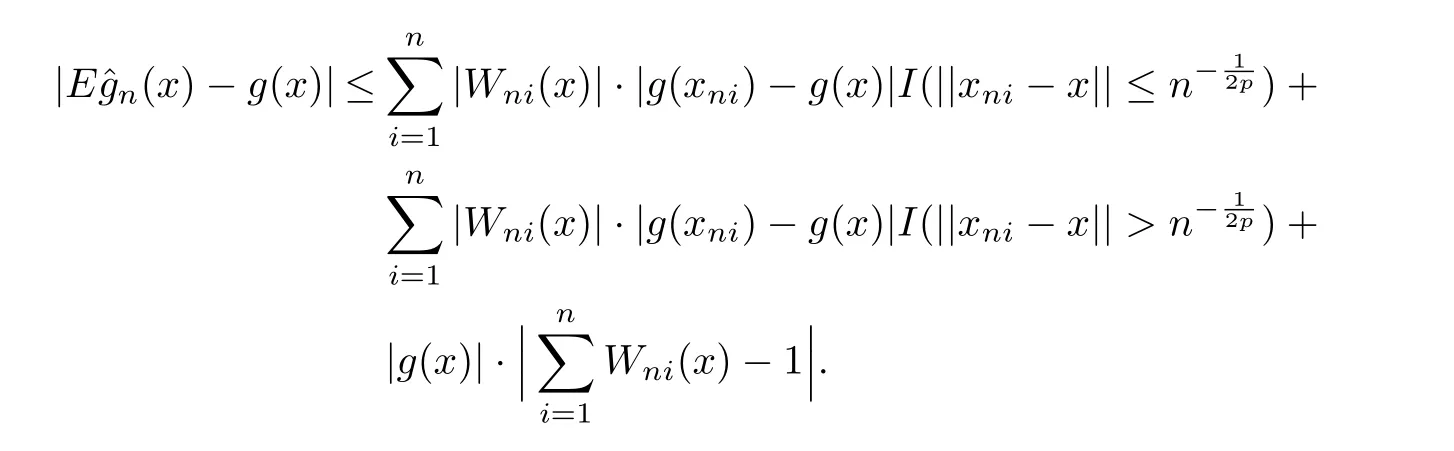
Since thatg(x)satisfies a local Lipschitz condition around the pointx,by(H1)-(H3)and the inequality above,we get that
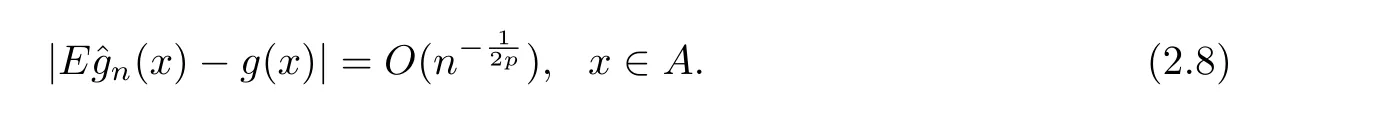
By the fact that for eachn,(εn1,...,εnn)has the same distribution as(ε1,...,εn),we establish that{Wni(x)εi,1≤i≤n}is also a mean zero-mixing sequence with the same mixing coefficients.Then,forx∈Aandp≥1,byEZ2p<∞,(H2)and Lemmas 1.1 and 1.2,we have that
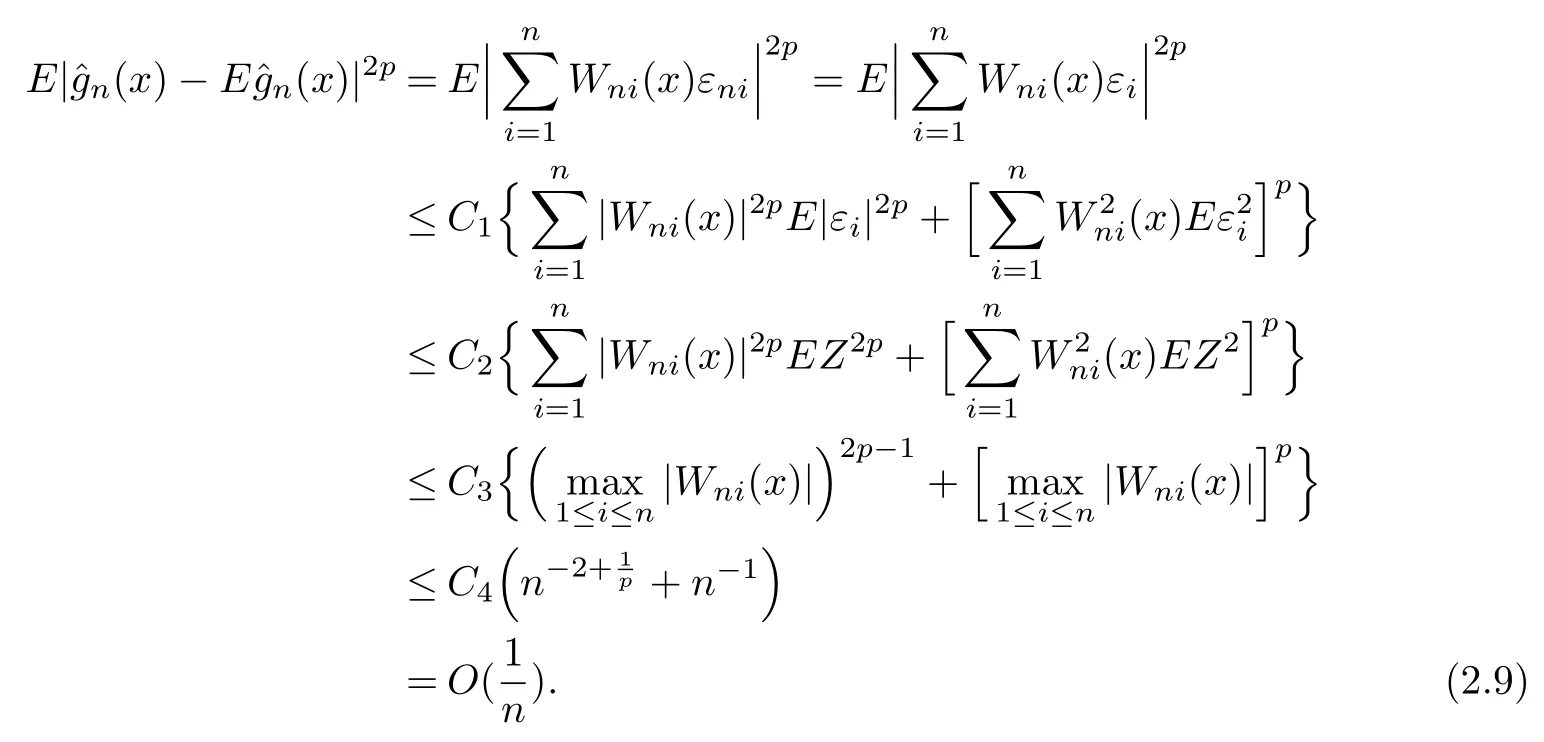
On the other hand,for somep≥1,it can be checked byCrinequality that

Therefore,(2.1)follows from(2.8)-(2.10)immediately.Last,by Markov inequality and(2.1),it has for allλ>0 that
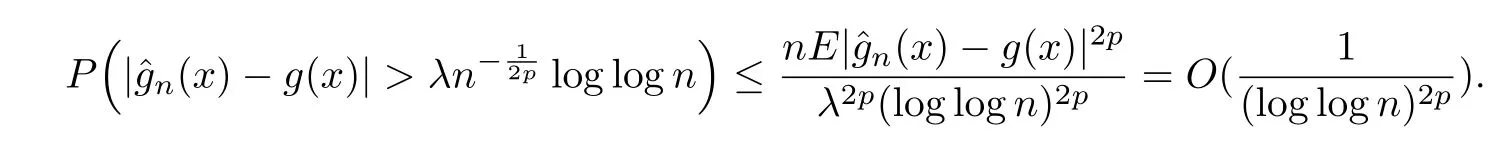
So we establish that the result of(2.2).
Acknowledgements
The authors are deeply grateful to the editor and the anonymous referees for their careful reading and insightful comments,which helped in improving an earlier version of this paper.
[1]STEIN S.A bound for the error in the normal approximation to the distribution of a sum of dependent random variables[J].Proc Sixth Berkeley Symp on Math Statist and Prob,1972,2:583-602.
[2]BRADLEY R C.Every “l(fā)owerψ-mixing” Markov chain is “interlacedρ-mixing”[J].Stochastic Process Appl,1997,72(2):221-239.
[3]BRADLEY R C.On the spectral density and asymptotic normality of weakly dependent random fields[J].J Theoret Probab,1992,5(2):355-373.
[4]PELIGRAD M.Maximum of partial sums and an invariance principle for a class of weak dependent random variables[J].Proc Amer Math Soc,1998,126(4):1181-1189.
[5]UTEV V,PELIGRAD M.Maximal inequalities and an invariance principle for a class of weakly dependent random variables[J].J Theoret Probab 2003,16(1):101-115.
[6]PELIGRAD M,GUT A.Almost-sure results for a class of dependent random variables[J]J Theoret Probab,1999,12(1):87-104.
[7]WU Qun-ying.Convergence properties ofρ-mixing random sequences[J].Chin J of Eng Math,2001,18(3):58-64 turn to 50.
[8]GAN Shi-xin.Almost sure convergence for-mixing random variable sequences[J].Stat Probab Lett,2004,67(4):289-298.
[9]KUCZMASZEWSKA A.On complete convergence for arrays of rowwise dependent random variables[J].Stat Probab Lett,2007,77(11):1050-1060.
[10]AN Jun,YUAN De-mei.Complete convergence of weighted sums forρ?-mixing sequence of random variables[J].Stat Probab Lett,2008,78(12):1466-1472.
[11]SUNG S H.Complete convergence for weighted sums ofρ?-mixing random variables[J].Discrete Dyn Nat Soc,2010,Article ID 630608,13 pages.
[12]WANG Xue-jun,LI Xiao-qin,YANG Wen-zhi,et al.On complete convergence for arrays of rowwiseweakly dependent random variables[J].Appl Math Lett,2012,25(11):1916-1920.
[13]SUNG S H.On the strong convergence for weighted sums ofρ?-mixing random variables[J].Stat Pap 2013,54(3):773-781.
[14]SUNG S H.On inverse moments for a class of nonnegative random variables[J].J Inequal Appl,2010,Article ID 823767,13 pages.
[15]HU Shu-he,WANG Xing-hui,YANG Wen-zhi,et al.A note on the inverse moment for the nonnegative random variables[J].Commun Stat Theory Methods,2014,43(8):1 750-1757.
[16]YANG Wen-zhi,HU Shu-he.Large deviation for a least squares estimator in a nonlinear regression model[J].Statist Probab Lett,2014,91:135-144.
[17]SHEN Ai-ting,ZHU Hua-yan,ZHANG Ying.Exponential inequalities and complete convergence for extended negatively dependent random variables[J].Chin Quart J of Math,2014,29(3):344-355.
[18]WU Yong-feng,SHEN Guang-jun.Complete moment convergence for arrays of rowwise negatively associated random variables[J].Chin Quart J of Math,2013,28(4):510-521.
[19]ZHENG Lu-lu,XU Chen,HUANG Xu-feng,et al.On the strong rates of convergence for arrays of rowwise extended negatively dependent random variables[J].Chin Quart J of Math,2014,29(4):592-601.
[20]WANG Xue-jun,XIA Feng-xi,GE Mei-mei,et al.Complete consistency of the estimator of nonparametric regression models based on-mixing sequences[J].Abstr Appl Anal,2012,Article ID 907286,12 pages.
[21]GEORGIEV A A,GREBLICKI W.Nonparametric function recovering from noisy observations[J].J Stat Plan Infer,1986,13(1):1-14.
[22]MüLLER H G.Weak and universal consistency of moving weighted averages[J].Period Math Hungar,1987,18(3):241-250.
[23]GEORGIEV A A.Consistent nonparametric multiple regression:the fixed design case[J].J Multivar Anal,1988,25(1):100-110.
[24]ROUSSAS G G,TRAN L T,IOANNIDES D A.Fixed design regression for time series:Asymptotic normality[J].J Multivar Anal,1992,40(2):262-291
[25]TRAN L,ROUSSAS G,YAKOWITZ S,et al.Fixed-design regression for linear time series[J].Ann Stat,1996,24(3):975-991.
[26]HU Shu-he,ZHU Chun-hua,CHEN Ye-bin.Fixed-design regression for linear time series[J].Acta Math Sci Ser B Engl Ed,2002,22(1):9-18.
[27]HU Shu-he,PAN Guang-min,GAO Qi-bing.Estimate problem of regression models with linear process errors[J].App1 Math J Chinese Univ Ser A,2003,18(1):81-90.
[28]LIANG Han-ying,JING Bing-yi.Asymptotic properties for estimates of nonparametric regression models based on negatively associated sequences[J].J Multivar Anal,2005,95(2):227-245.
[29]YANG Wen-zhi,WANG Xue-jun,WANG Xing-hui,et al.The consistency for estimator of nonparametric regression model based on NOD errors.J Inequal Appl,2012,2012:140,pages 13.
[30]PENG Zhi-qing,ZHENG Lu-lu,LIU Yan-fang,et al.Asymptotic property for the estimator of nonparametric regression models under negatively orthant dependent errors[J].Chin Quart J of Math,2015,30(2):300-307.
[31]ADLER A,ROSALSKY A.Some general strong laws for weighted sums of stochastically dominated random variables[J].Stoch Anal Appl 1987,5(1):1-16.
[32]ADLER A,ROSALSKY A,TAYLOR R L.Strong laws of large numbers for weighted sums of random elements in normed linear spaces[J].Int J Math Math Sci,1989,12(3):507-530.
[33]WU Qun-ying.Probability Limit Theory for Mixed Sequence[M].Science Press,Beijing 2006.
[34]HANSON D L,WRIGHT F T.A bound on tail probabilities for quadratic forms in independent random variables[J].Ann Math Statist,1971,42(3):1079-1083.
[35]WRIGHT F T.A bound on tail probabilities for quadratic forms in independent random variables whose distributions are not necessarily symmetric[J].Ann Probab,1973,1(6):1068-1070.
 Chinese Quarterly Journal of Mathematics2017年4期
Chinese Quarterly Journal of Mathematics2017年4期
- Chinese Quarterly Journal of Mathematics的其它文章
- Fekete-Szeg? Problem for Certain Subclass of p-Valent Analytic Functions using Quasi-Subordination
- Global Stability of A Stochastic Predator-prey Model with Stage-structure
- A Kind of Identities Involving Complete Bell Polynomials
- Recover Implied Volatility in Short-term Interest Rate Model
- Adjacent Vertex Distinguishing I-total Coloring of Outerplanar Graphs
- The 1-Good-neighbor Connectivity and Diagnosability of Locally Twisted Cubes
