(王文元)

School of Mathematics and Statistics, Fujian Normal University, Fuzhou 350007, China;School of Mathematical Sciences, Xiamen University, Xiamen 361005, China E-mail: wywang@fjnu.edu.cn

Ruixing MING (明瑞星)?

School of Statistics and Mathematics, Zhejiang Gongshang University, Hangzhou 310018, China E-mail: rxming@zjgsu.edu.cn

Yijun HU (胡亦鈞)

School of Mathematics and Statistics, Wuhan University, Wuhan 430071, China E-mail: yjhu.math@whu.edu.cn

Abstract Motivated by recent advances made in the study of dividend control and risk management problems involving the U.S.bankruptcy code, in this paper we follow [44] to revisit the De Finetti dividend control problem under the reorganization process and the regulator’s intervention documented in U.S.Chapter 11 bankruptcy.We do this by further accommodating the fixed transaction costs on dividends to imitate the real-world procedure of dividend payments.Incorporating the fixed transaction costs transforms the targeting optimal dividend problem into an impulse control problem rather than a singular control problem, and hence computations and proofs that are distinct from [44] are needed.To account for the financial stress that is due to the more subtle concept of Chapter 11 bankruptcy,the surplus process after dividends is driven by a piece-wise spectrally negative L′evy process with endogenous regime switching.Some explicit expressions of the expected net present values under a double barrier dividend strategy, new to the literature, are established in terms of scale functions.With the help of these expressions, we are able to characterize the optimal strategy among the set of admissible double barrier dividend strategies.When the tail of the L′evy measure is log-convex, this optimal double barrier dividend strategy is then verified as the optimal dividend strategy, solving our optimal impulse control problem.

Key words spectrally negative L′evy process;Chapter 11 bankruptcy;De Finetti’s dividend problem; double barrier strategy; impulse control

1 Introduction

As an alternative risk management tool to that of ruin probability, De Finetti’s dividend control problem has remained an active research topic in corporate finance and insurance for decades, mainly due to its effectiveness in signaling the health and stability of financial companies.The goal of this type of risk management is to maximize the expected total net present value (NPV) of accumulated dividend payments, which is conventionally referred to as the value of the company.The literature of the past decades has witnessed fruitful research (see[16, 17, 21, 42] for some early works along these lines) on De Finetti’s dividend optimization involving stochastic regular,singular,or impulse control problems under a number of risk models, among which the spectrally negative L′evy risk model has been gaining in popularity in insurance applications, due to its capability to model the reserve process of an insurance company that collects premiums continuously and pays claim payments in lump sums.Early works on De Finetti’s dividend control problem under the spectrally negative L′evy risk model are[6, 25, 31, 32, 41]; see also the references therein.In particular, the works of [6, 31, 32, 43-45]verified that the optimal dividend strategy yielding the maximum NPV of accumulated dividends is the barrier strategy, here the fluctuation theory of spectrally negative L′evy processes and the standard approach of the Hamilton-Jacobi-Bellman(HJB)equation was adopted.For a more comprehensive review of developments in optimal dividends and the related methodology,we refer to two survey papers,[1]and[3],where thorough and insightful reviews on the classical contributions and recent progress in the dividend control field are provided.In addition, a variety of recent works have taken into account new and different risk factors, control constraints or model generalizations; see, for example, [4, 5, 10, 11, 15, 22, 28, 35, 36, 39, 43, 44, 46], etc..

In recent years, the modelling of the liquidation process (Chapter 7 bankruptcy) and the reorganization process (Chapter 11 bankruptcy) written in the bankruptcy code of the United States has attracted more and more research attention among at the insurance and finance communities; see, [8, 9, 13, 14, 27, 37] as well as the references therein.To get a real-world picture of Chapter 7 and Chapter 11 bankruptcy, [29] used a piece-wise time-homogeneous diffusion process, as well as three constant barrier levels,a,bandc(a ＜b ＜c), to model the reserve process of an insurance company.The lower barrierarepresents the liquidation barrier, i.e., once the reserve process falls belowa, the company is liquidated because its assets can no longer cover its debts.The middle barrierbrepresents the reorganization barrier, i.e.,once the reserve process falls belowb, the insurer enters a state of insolvency (the businesses of an insolvent insurer are subject to reorganization under the interventions of the regulator),and it may either return to the solvent state (a solvent insurer is free of interventions) if the reserve process recovers to the upper barriercwithin the grace period granted by the regulator,or it remains in a state of insolvency and is then liquidated.The upper barriercrepresents the solvency barrier, i.e., an insurer who possesses a reserve above this barrier is solvent, since it is able to meet its liabilities, and the solvent insurer will not switch to the insolvent state unless the reserve process falls belowbat some future time.In addition, the dynamics of the reserve process, subject to the state of the insurer, switches between two time-homogeneous diffusion processes with different drifts and volatilities.[29] obtained closed-form expressions of the liquidation probability and the Laplace transform of the liquidation time.

Inspired by the above mentioned works on the De Finetti dividend problems and the financial modelling of the liquidation and reorganization process, [44]considered a variant of the De Finetti optimal dividend control problem by incorporating an appealing feature of Chapter 11 bankruptcy to the piece-wise spectrally negative L′evy risk processes embedded with a reorganization barrierband a solvency barrierc(b ＜c); it turned out that a single barrier dividend strategy is the optimal dividend strategy.In this paper, to better imitate the realworld procedure of dividend payments, we would like to incorporate the real-life factor of fixed transaction costs on dividends into our new targeting variant for the De Finetti dividend optimization problem.In addition, we follow[44]in assuming that the uncontrolled reserve process(i.e., free of dividends) evolves as two spectrally negative L′evy processes switching between each other, where a change in the state of the insurer triggers a switch of the dynamics of the reserve process.To match the real life situation, we also assume that dividends are paid only when the reserve is higher thanc.An analytical characterization of the optimal strategy in the set of all double barrier admissible dividend strategies is provided.Then important properties of the optimal double barrier levels are studied.A sufficient condition that the L′evy measure has a log-convex tail is finally found; under that our optimal control problem is solvable, in that the optimal double barrier dividend strategy dominates all admissible impulse dividend strategies.We mention that, since no fixed transaction costs are considered, the dividend optimization problem addressed in [44] is a singular control problem.With the presence of fixed transaction costs, our new control problem becomes an impulse control problem, rather than a singular control problem as in [44].Therefore, compared with [44], we need distinct computations and arguments to solve our control problem and characterize the optimal impulse dividend strategy; for example, some different deep understandings of the scale functions and delicate computations on generators and slope conditions are needed.Another contribution of the current paper lies in that it helps understanding of how the impulse dividend decision can be affected by reorganization and by regulator’s intervention for a concrete example, see Section 4, where detailed discussions are provided.

The rest of the paper is organized as follows: some preliminary results on spectrally negative L′evy processes are presented in Section 2.Section 3 focuses on solving De Finetti’s optimal impulse dividend control problem by accommodating fixed transaction costs under Chapter 11 bankruptcy; here the optimal impulse control is shown to fit the double-barrier type dividend strategy by following a “guess-and-verify” procedure.In Section 4, a concrete example is provided and analyzed to illustrate the main results obtained in Section 3.

2 Preliminaries on Spectrally Negative L′evy Processes

We collect in this section some elementary facts on the spectrally negative L′evy processes;interested readers may refer to [23] for more details.A spectrally negative L′evy process is an upward-jump-free stochastic process having stationary and independent increments.Denote byX={X(t);t ≥0}a spectrally negative L′evy process defined on a filtered probability space(Ω,{Ft;t ≥0},P) satisfying the usual conditions.To avoid trivialities, we assume thatXhas no monotone paths.Let Pxbe the conditional probability, given thatXstarts fromx, and let Exbe the corresponding expectation operator.For simplicity, write P and E for P0and E0,respectively.The Laplace transform ofXis given by

We recall that the scale functionWqis left and right differentiable atx ∈(0,∞).Furthermore,Wqis continuously differentiable on (0,∞) ifXhas sample paths of unbounded variation or has sample paths of bounded variation and the L′evy measure is atomless; in particular, it is twice continuously differentiable on (0,∞) ifXhas a nontrivial Gaussian component.We are refer to [31] for more analytical properties of the scale functions.To make our impulse control problem solvable, we shall assume throughout this paper that the tail of the L′evy measureυis log-convex, and hence the scale functionWq(x) is continuously differentiable andW′q(x) is log-convex, implying thatW′q(x) is right and left differentiable over (0,∞) and is differentiable over (0,∞) except for countably many points.In the sequel, byW′′q(x), we mean the right derivative ofW′q(x) whenW′q(x) is not differentiable atx.

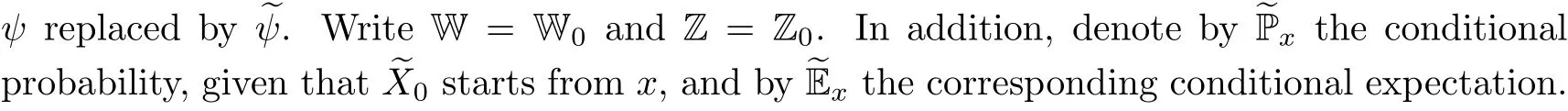
3 De Finetti’s Optimal Dividend under Chapter 11 Bankruptcy and Fixed Transaction Costs

This section investigates De Finetti’s optimal dividend control problem with fixed transaction costs on dividends under the Chapter 11 bankruptcy is written in the U.S.bankruptcy code.To describe the dynamics of switching under the regulator’s intervention, we introduce an auxiliary state processI(t), subject to the dividend control, as an indicator of the process of solvency and insolvency states.Supposing that the insurer is solvent at timet ≥0 (i.e.,I(t) = 0), it remains solvent until the reserve processUfalls below the reorganization barrierb, at which time the state of the insurer is switched to that of insolvency.On the other hand, if the insurer is in the insolvent state at timet ≥0(i.e.,I(t)=1),then it remains in the insolvent state until the reserve process climbs up to the safety barrierc, at which period the state of the insurer is switched to that of being solvent.As a result, the dynamics of the reserve processUfollows as a spectrally negative L′evy processXdeduced with dividends whenever the insurer is solvent, andUis governed by the spectrally negative L′evy processXwhenever the insurer is insolvent.We mention that Chapter 11 bankruptcy takes place if the insurer stays continuously in a state of insolvency for a time interval greater than that of the grace time limit granted by the regulator.It also needs to be mentioned that, due to the additional costs at the time of dividend payment, we shall restrict the admissible controls to impulse dividend strategies,instead of regular or singular dividend strategies.

3.1 Problem Formulation

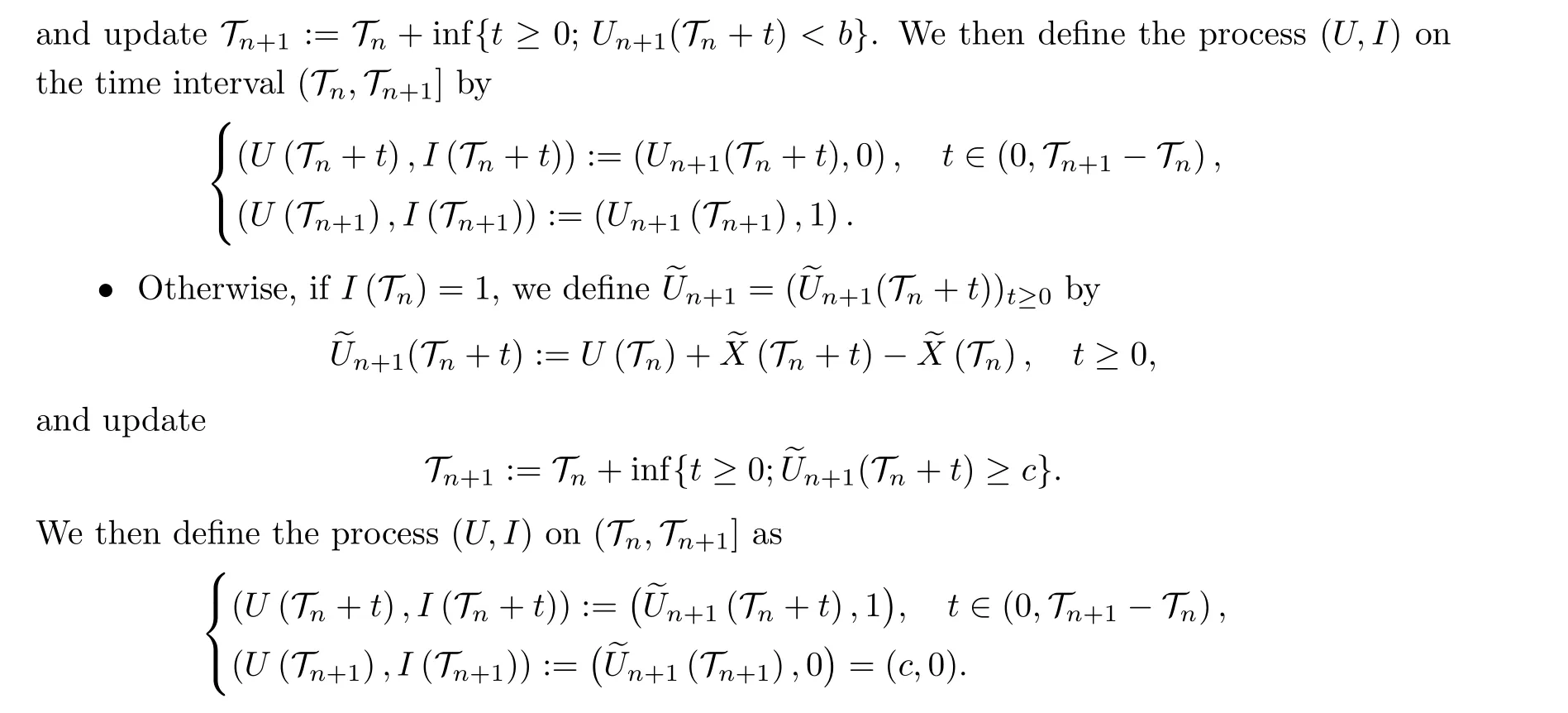
(b) Supposing that the process (U,I) has been defined on [0,Tn] for somen ≥0 withTn=∞, we updateTn+1=∞.

Let us denote byDthe set of all admissible impulse dividend controls, which consists of all pure-jump non-decreasing and left-continuous F-adapted processes.For an admissible impulse dividend controlD ∈D, we consider the next two expected NPVs with the fixed unit transaction costφsuch that

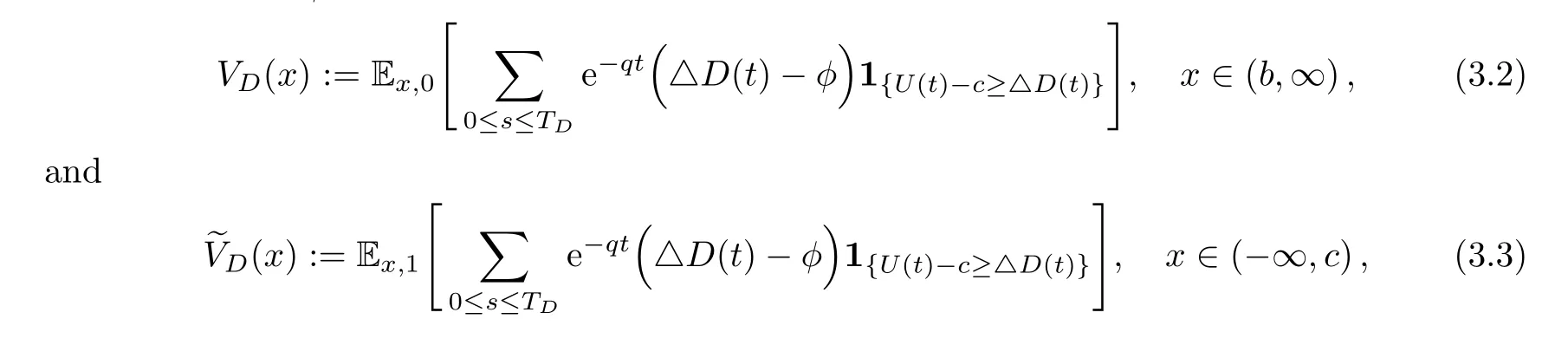
3.2 Expected NPVs of Dividends under a Double Barrier Strategy

which completes the proof.□

3.3 Optimal Double Barriers and Verification of the Optimality

For fixedbandcsuch that-∞＜b ＜c ＜∞, let us define the auxiliary function

which stands for the set of the maximizers of the above bi-variate functionξ.The following lemma investigates some properties ofMthat are useful for further computations and analysis;see Proposition 3.2 and the proof of Lemma 3.3, etc.:

Lemma 3.3The setMdefined in (3.12) is non-empty, and there exists az0∈(c,∞)such that

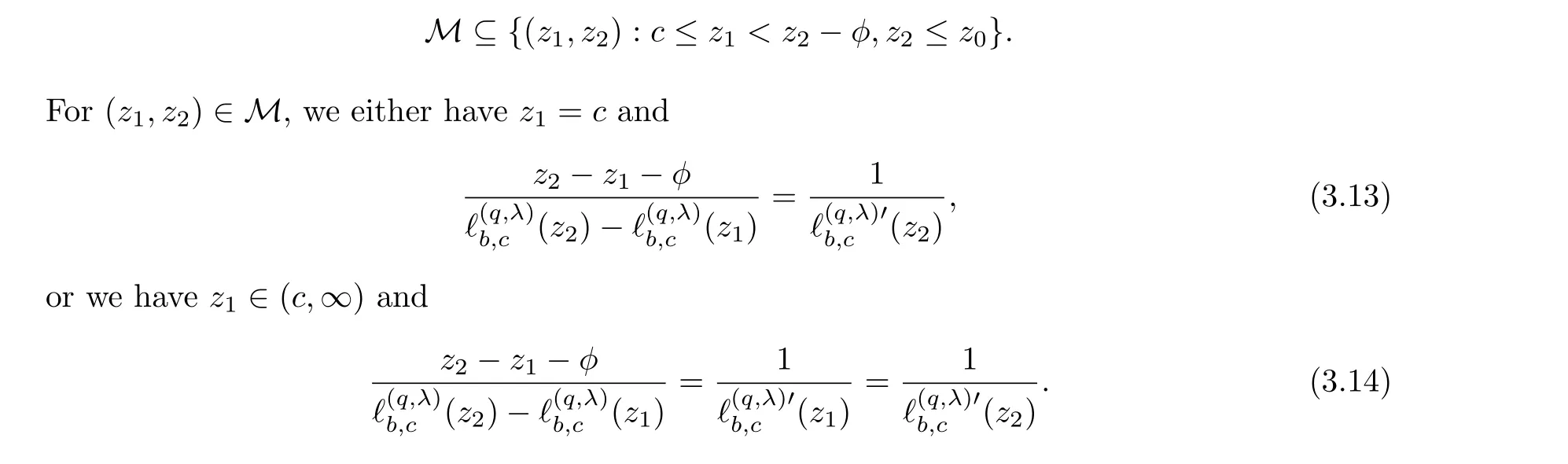
ProofFrom (2.1) and the L’H?ospital’s rule, it can be verified that

Proposition 3.4For (z1,z2)∈M, we have that

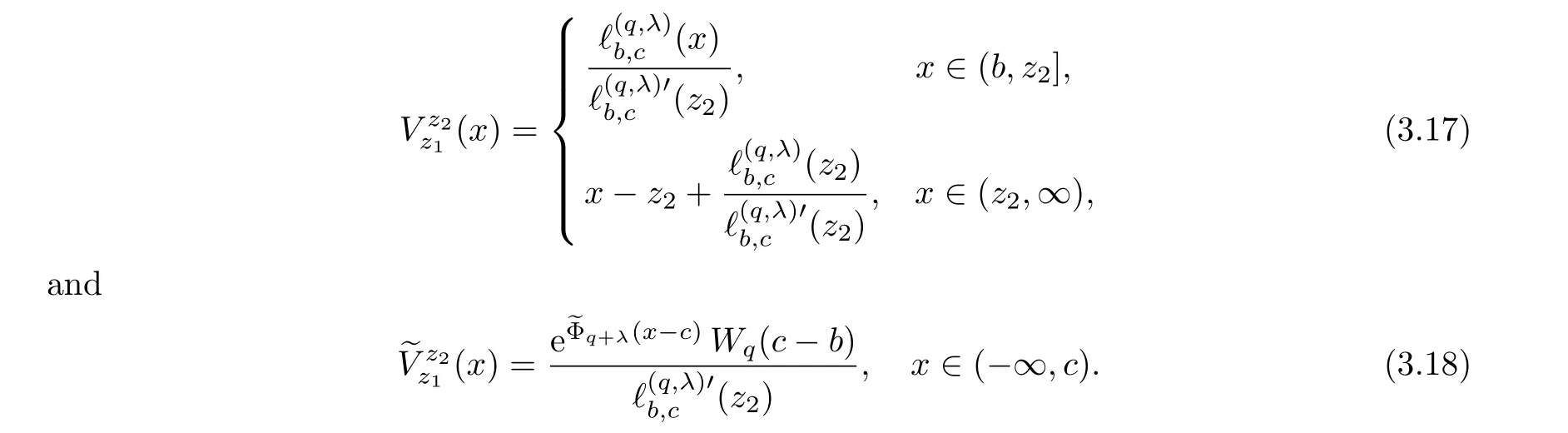
By the definition ofξ,Proposition 3.1 and Lemma 3.1,it seems reasonable to take a double barrier (z1,z2)∈Mdividend strategy as the candidate optimal strategy among the set of all admissible double barrier dividend strategies.As is stated above, we aim to show that the optimal impulse dividend control under fixed transaction costs fits this type of double barrier dividend strategy.To this end,we guess that the double barrier(z1,z2)∈Mdividend strategy is the optimal one among the set of all admissible impulse dividend strategies, and verify in the next lemma that its value function fits the Hamilton-Jacobi-Bellman (HJB) inequality to which the optimal value function should fit.

Lemma 3.5For (z1,z2)∈M, we have that

Putting all of the pieces together completes the proof.□

ProofFor a given strategyD ∈Dand the resulting surplus processU,given by Definition 3.1,we denote(Uc(t))t≥0as the continuous part of(U(t))t≥0.In addition,for a positive integerN ≥1, let us defineηN:=inf{t ≥0:|U(t)|＞N}as the sequence of localizing stopping times.By definition, it holds that, fort ＜ηN,

Theorem 3.8Suppose that the tail of the L′evy measure is log-convex.Recall thatMis as defined in (3.12).The double barrier (z1,z2)∈Mdividend strategy is the optimal impulse dividend strategy achieving the maximal value function up to the Chapter 11 bankruptcy time.

4 An Illustrative Example

Under the mild condition that the L′evy measure ofXhas a log-convex tail, Theorem 3.8 verifies that the double barrier dividend strategy with barriers (z1,z2)∈Mserves as the optimal impulse dividend strategy,and yields the maximum expected discounted total dividends(subtracting with transaction costs).To compute explicitly the two barriers of the optimal impulse dividend strategy, we consider the Cram′er-Lundberg processXwith exponential jump sizes; namely, a processXdefined by a deterministic driftp(the premium income) subtracting a compound Poisson process with jump intensityλ0and exponentially distributed jump sizes with a mean of 1/μ.It is well known that

·c ＜x0andφ0≤φ ＜x1-c.From (4.3) we have thatg(c)＞0, which, together with the fact thatgis strictly increasing, yields thatg(x)＞0 for allx ∈[c,x0], which contradicts the first equation in (3.14).Hence, there should not be an interior local maximum point ofξ,which implies thatMreduces to a singleton, i.e.,M={(c,z2)}withz2∈(x0,∞) being the unique solution of (4.2).

Conflict of InterestThe authors declare no conflict of interest.