郝國亮,吳愉琪,曾淑婷

(1.東華理工大學(xué)理學(xué)院,江西 南昌 330013;2.菏澤學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,山東 菏澤 274015)

1 預(yù)備知識

近幾十年來,基于不同的應(yīng)用背景,圖的控制參數(shù)問題得到了廣泛研究.[1-2]1999年,Stewart[3]提出了君士坦丁大帝時(shí)期防御羅馬帝國的策略“Defend the Roman Empire”.基于該策略,Cockayne等[4]引入了圖的羅馬控制的概念.2016年,Chellali等[5]將“Defend the Roman Empire”中的防御策略弱化,提出了圖的羅馬{2}-控制數(shù)的概念.隨后,羅馬{2}-控制被Henning等[6]重新命名為意大利控制.Gao等[7]計(jì)算了笛卡爾乘積圖的意大利控制數(shù)的精確值.Varghese等[8]研究了邊的增加對意大利控制數(shù)的影響.Banerjee等[9]給出了計(jì)算余圖的完美意大利控制數(shù)的線性時(shí)間算法.本文將研究圖的全局意大利控制問題,給出了一般圖的全局意大利控制數(shù)的界并且得到了某些特殊圖的全局意大利控制數(shù)的精確值.

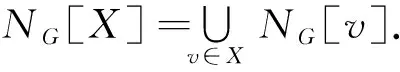
2 主要結(jié)論及其證明

命題1 對任意n階圖G,min{n,4}≤γgI(G)≤n.

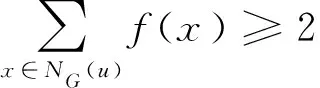
由于0

證明當(dāng)n∈{3,4}時(shí),由命題1知,γgI(Fn)=n.設(shè)n≥5且設(shè)扇形圖Fn是由路Pn-1=v2v3…vn和一個(gè)不在路Pn-1上的頂點(diǎn)v1組成,且使得v1與其他頂點(diǎn)都相鄰.

若5≤n≤10,由命題1,要證明γgI(Fn)=4成立,只需要證明γgI(Fn)≤4即可.如果n=5,則定義F5的全局意大利控制函數(shù)g使得g(v5)=0,且當(dāng)i≠5時(shí)g(vi)=1,于是γgI(F5)≤ω(g)=4;如果n∈{6,7},則定義Fn的全局意大利控制函數(shù)g使得當(dāng)i∈{1,2,5,6}時(shí)g(vi)=1,且當(dāng)i?{1,2,5,6}時(shí)g(vi)=0,于是γgI(Fn)≤ω(g)=4;如果n∈{8,9},則定義Fn的全局意大利控制函數(shù)g使得當(dāng)i∈{1,2,5,8}時(shí)g(vi)=1,且當(dāng)i?{1,2,5,8}時(shí)g(vi)=0,于是γgI(Fn)≤ω(g)=4;如果n=10,則定義F10的全局意大利控制函數(shù)g使得當(dāng)i∈{1,3,6,9}時(shí)g(vi)=1,且當(dāng)i?{1,3,6,9}時(shí)g(vi)=0,于是γgI(F10)≤ω(g)=4.

若n≥11,定義Fn的全局意大利控制函數(shù)g使得g(v1)=g(v2)=2,g(v3)=1且當(dāng)i?{1,2,3}時(shí),g(vi)=0,故γgI(Fn)≤5.往證γgI(Fn)≥5.由命題1,只要證明γgI(Fn)≠4即可.反證法.假設(shè)γgI(Fn)=4,令f是γgI(Fn)-函數(shù),則ω(f)=γgI(Fn)=4.

斷言1f(v1)=1.

這與f是γgI(Fn)-函數(shù)矛盾.因此f(v1)=1.斷言1得證.

斷言2f(vi-1)+f(vi)+f(vi+1)≥1,其中3≤i≤n-1.

事實(shí)上,若結(jié)論不真,則存在3≤i≤n-1使得f(vi-1)=f(vi)=f(vi+1)=0.則由斷言1知,

這與f是γgI(Fn)-函數(shù)矛盾.斷言2得證.

因?yàn)閚≥11,所以由斷言1和斷言2可得

易見上式中“=”成立.因此f(v2)=f(vn)=0.又因?yàn)閒(v1)=1,所以由γgI(Fn)-函數(shù)的定義知,f(v3)≥1且f(vn-1)≥1.因此由斷言1和2知,

矛盾.于是當(dāng)n≥11時(shí),γgI(Fn)≠4.

證明當(dāng)n∈{3,4}時(shí),由命題1知,γgI(Wn)=n.下設(shè)n≥5且設(shè)輪圖Wn是由圈Cn-1=v2v3…vnv2和一個(gè)不在圈上的頂點(diǎn)v1組成,且使得v1與其他頂點(diǎn)都相鄰.

假設(shè)n∈{6,8,10}.由命題1,要證明γgI(Wn)=4成立,只需證明γgI(Wn)≤4即可.如果n=6,則定義W6的全局意大利控制函數(shù)g使得當(dāng)i∈{2,3}時(shí)g(vi)=0,且當(dāng)i?{2,3}時(shí)g(vi)=1,于是γgI(W6)≤ω(g)=4;如果n∈{8,10},則定義Wn的全局意大利控制函數(shù)g使得當(dāng)i∈{1,2,5,8}時(shí)g(vi)=1,且當(dāng)i?{1,2,5,8}時(shí)g(vi)=0,于是γgI(Wn)≤ω(g)=4.

假設(shè)n∈{5,7,9}或n≥11.定義W5的全局意大利控制函數(shù)g使得對任意i∈{1,2,3,4,5},g(vi)=1,于是γgI(W5)≤ω(g)=5.當(dāng)n∈{7,9}或n≥11時(shí),定義Wn的全局意大利控制函數(shù)g使得g(v1)=2,當(dāng)i∈{2,3,4} 時(shí)g(vi)=1,且當(dāng)i?{1,2,3,4} 時(shí)g(vi)=0,于是γgI(Wn)≤ω(g)=5.接下來證明:當(dāng)n∈{5,7,9}或n≥11時(shí),γgI(Wn)≥5.由命題1,只需要證明γgI(Wn)≠4.用反證法.假設(shè)γgI(Wn)=4,令f是γgI(Wn)-函數(shù),則ω(f)=γgI(Wn)=4.

斷言1f(v1)=1且對任意i∈{2,3,…,n},f(vi)∈{0,1}.

事實(shí)上,類似于定理2中斷言1 的證明可得f(v1)=1.往證對任意i∈{2,3,…,n},f(vi)∈{0,1}.用反證法.不失一般性,若f(v2)?{0,1},則顯然f(v2)=2.于是

因此f(v3)和f(vn)中至少一個(gè)為0,不妨假設(shè)f(v3)=0,于是

這與f是γgI(Wn)-函數(shù)矛盾.因此對任意i∈{2,3,…,n},f(vi)∈{0,1}.斷言1得證.

類似于定理2 中斷言2 的證明可得如下斷言:

斷言2f(vi)+f(vj)+f(vk)≥1,其中2≤i,j,k≤n且NWn(vj)-{v1}={vi,vk}.

斷言3 不存在3個(gè)頂點(diǎn)vi,vj和vk使得f(vi)=f(vk)=1且f(vj)=0,其中2≤i,j,k≤n且NWn(vj)-{v1}={vi,vk}.

事實(shí)上,若結(jié)論不真,不失一般性,假設(shè)f(v2)=f(v4)=1且f(v3)=0.又因?yàn)閒(v1)=1,所以

這與f是γgI(Wn)-函數(shù)矛盾.于是斷言3得證.

與假設(shè)γgI(Wn)=4矛盾.

綜上所述,對任意n∈{5,7,9}或n≥11,γgI(Wn)≠4.