一道2022年江西預(yù)賽試題的多解探究與變式
成 敏 徐鳳旺 尹正波
貴州師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院 (550025)
1 試題呈現(xiàn)
分析:這是2022年全國(guó)高中數(shù)學(xué)聯(lián)賽江西賽區(qū)的一道根式函數(shù)求最大值的試題.文[1]通過(guò)三種方法求得該函數(shù)的最大值,并對(duì)其試題進(jìn)行了相應(yīng)的變式,讀后深受啟發(fā),于是對(duì)該題做進(jìn)一步的探究,得到了不同于文[1]中的三種解法和試題的幾個(gè)變式,與大家一起分享.
2 試題解析
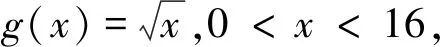
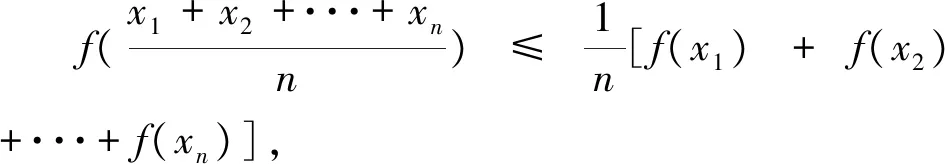
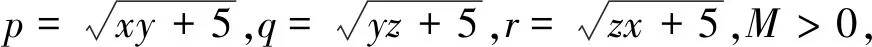
評(píng)注:此解法通過(guò)換元法,構(gòu)造二次函數(shù),將問(wèn)題轉(zhuǎn)化為二次函數(shù)的Δ≤0,即可求得該函數(shù)的最大值.
解法3:(構(gòu)造隨機(jī)變量X的分布列)由題意可得,可構(gòu)造隨機(jī)變量X的分布列為:

Xxy+5yz+5zx+5P131313
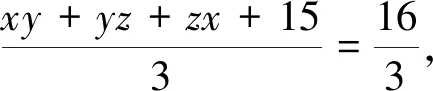
評(píng)注:此解法通過(guò)構(gòu)造隨機(jī)變量X的分布列,結(jié)合(EX)2≤EX2,求得函數(shù)的最大值.
3 試題變式
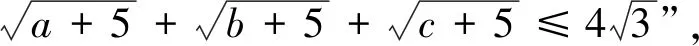
3.1 三元形式的變式
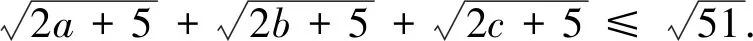

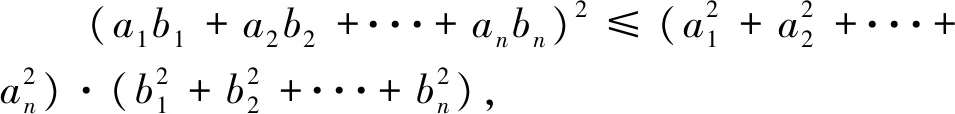
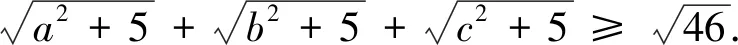
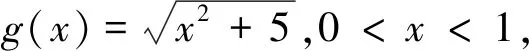
評(píng)注:此變式是將不等式每一項(xiàng)根號(hào)下未知數(shù)的冪從“1”變?yōu)椤?”得到.
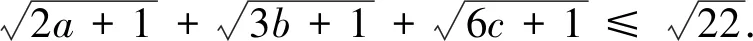

評(píng)注:此變式是將不等式每一項(xiàng)根號(hào)下的未知數(shù)的系數(shù)和常數(shù)項(xiàng)改變得到.
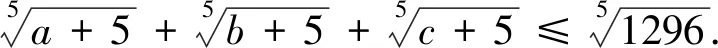
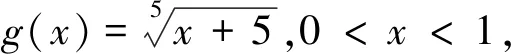
評(píng)注:此變式是通過(guò)改變不等式每一項(xiàng)的冪得到.
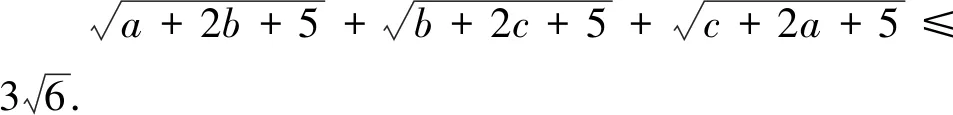
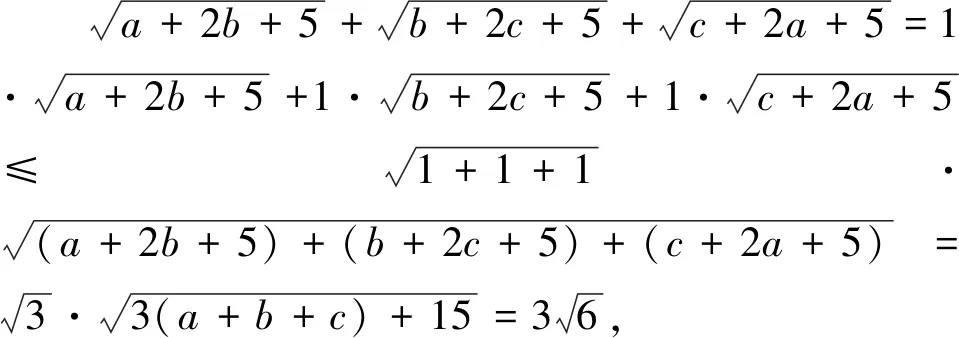
評(píng)注:此變式是通過(guò)改變不等式每一項(xiàng)根號(hào)下的代數(shù)式的結(jié)構(gòu)得到,將每一項(xiàng)根號(hào)下未知數(shù)的個(gè)數(shù)從“1”元變?yōu)椤?”元.
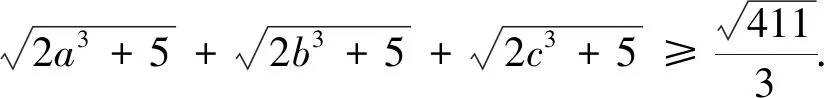
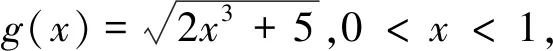
評(píng)注:此變式是通過(guò)改變不等式每一項(xiàng)根號(hào)下的未知數(shù)的冪和系數(shù)得到.
3.2 四元形式的變式


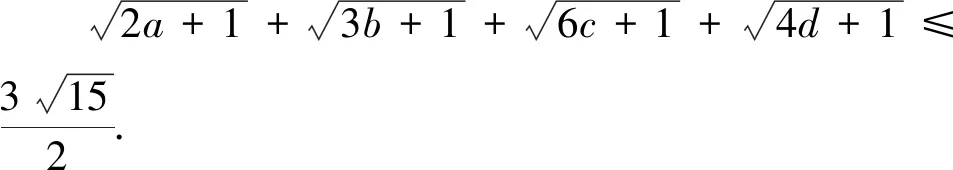
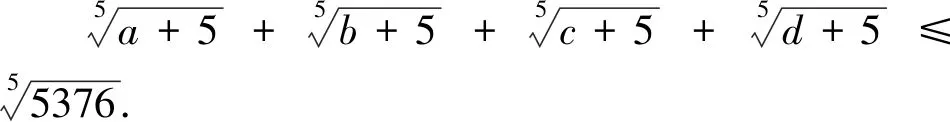
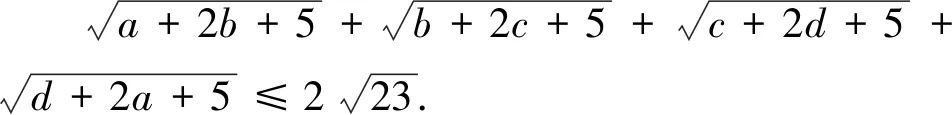

上述變式7到變式12均是在變式1到變式6的基礎(chǔ)上改變的,將未知數(shù)的個(gè)數(shù)從“3”元變到“4”元,變式7到變式12的證明方法分別對(duì)應(yīng)變式1到變式6的證明方法,證明方法一致,此處不再敘述.

