Shuxuan Wu(吳書(shū)旋) Zengtai Zhu(朱增泰) Yunxu Ma(馬云旭) Jinwu Wei(魏晉武)Senfu Zhang(張森富) Jianbo Wang(王建波) and Qingfang Liu(劉青芳)

1Key Laboratory for Magnetism and Magnetic Materials of the Ministry of Education,Lanzhou University,Lanzhou 730000,China

2Songshan Lake Materials Laboratory,Dongguan 523808,China

3Key Laboratory for Special Function Materials and Structural Design of the Ministry of the Education,Lanzhou University,Lanzhou 730000,China

We investigated the angle-dependent spin wave spectra of permalloy ring arrays with the fixed outer diameter and various inner diameters by ferromagnetic resonance spectroscopy and micromagnetic simulation. When the field is obliquely applied to the ring, local resonance mode can be observed in different parts of the rings. And the resonance mode will change to perpendicular spin standing waves if the magnetic field is applied along the perpendicular direction. The simulation results demonstrated this evolution and implied more resonance modes that maybe exist. And the mathematical fitting results based on the Kittel equation further proved the existence of local resonance mode.

Keywords: spin waves,magnetic resonance spectra,spintronic devices

1. Introduction

Periodically magnetic patterned structures have been extensively studied in the last decades.[1–8]As the progress of nanofabrication techniques, it is possible to prepare the nanoscale or submicron-scale pattern arrays on the magnetic films. To date, the arrays of dots, rings, and wires have been investigated by experimental observation or micromagnetic simulation.[4,9–13]Magnetic patterned films have opened the possibility of studying and designing the new magnetic storage, magnetic logic and spintronic devices. For example,there have been many studies on nanoring magnetic tunnel junctions.[14–17]Their static and dynamic magnetic properties strongly depend on the size and topological structures. The patterned magnetic films are also known as the magnonic crystals. As the propagation of light in the photonic crystals, the propagation properties of spin waves in the magnonic crystals can be modified by the well-designed patterns.[18]Therefore,magnonic crystals are considered to offer new functionalities that are unavailable in regular electronic devices. Depending on the scale of magnetic pattern structures,exchange interaction and dipolar interaction play significant roles,respectively.In fact, the patterns introduce a kind of size confine, which makes the magnetization motion become very different from that in the continuous films. Demagnetizing field, edge pinning and anisotropy of patterns are all supposed to be important for the magnetic properties of patterned films.[5,11,19]

Although the ferromagnetic resonance (FMR) spectra of patterned films have been wisely researched, recent studies showed rich spin wave spectra of magnetic disks and rings at different magnetized states.[13,20,21]For example,when the magnetic field was applied in the film plane, the magnetic disks at remanence showed a magnetization transition from onion to vortex state depending on the magnitude of the applied field.[22–24]On the other hand, splitting of excitation spectra was observed if the magnetic rings magnetized along the direction of out-of-plane.[21]Furthermore, the resonance spectra of ring arrays are more complex than those of disks because of the unique topological structure of rings. In other words, disks are internally connected but rings are not. The geometric ring will introduce the radial demagnetizing field,which provides more dimensions to design the spintronic devices or storage the information. The more complex structure represents more difficulties in manipulating the performance of rings. The previous research focused on the FMR spectra and dynamic magnetic properties of rings. Multi-peak resonance was always observed at both vertical and horizontal magnetization states. However,the evolution of resonance modes is still not clear, which is important to understand and adjust the dynamic magnetic properties of rings.

In this paper, we prepared a series of permalloy ring arrays with the fixed outer diameter and various inner diameters and presented the observation of FMR spectra when the applied magnetic field rotated from in-plane to out-of-plane direction. Several absorption modes were observed at different magnetized angles. Micromagnetic simulations qualitatively agree with the experimental results and indicate the evolution of resonance modes. When the field is applied obliquely, the local resonance modes depend on the magnetic field magnitude,while the perpendicular spin standing wave(PSSW)can be observed if the magnetic field is applied vertically. Mathematical fitting results further prove the evolution pattern of resonance modes.

2. Experimental and simulation methods

Isotropic permalloy(Py,Fe20Ni80)film was deposited on Si(100)wafer by radio frequency magnetron sputtering technique. The base pressure of the sputtering chamber was better than 5×10-5Pa. Based on the sectional images of scanning electron microscopy (SEM), the thickness of the permalloy film was about 220 nm. The as-deposited film was divided into several 5 mm×5 mm square chips. Periodic ring arrays were fabricated on the prepared samples by using a laser direct write lithography (DWL, Heidelberg 66FS) and lift-out processes. The outer diameters(D)of rings were fixed at 30 μm.The inner diameters(d)were 10 μm,15 μm, 20 μm, 25 μm,respectively. The space between centers of rings was kept at 40 μm.For convenience,the samples withdof 10 μm,15 μm,20 μm, 25 μm are represented as sample 1–4, respectively.The morphology of the prepared ring arrays was characterized by field emission scanning electron microscopy(FESEM,Tescan Mira 3 xmu, Czech Republic). Dynamic properties were characterized by electron spin resonance (ESR, JES-FA300)commercial equipment. All measurements were conducted at room temperature.

To validate the experimental results,micromagnetic simulation is performed by the MuMax3 code.[25]The magnetization dynamics of a ring is governed by the Landau–Lifshitz–Gilbert(LLG)equation[26]

whereMrepresents the magnetization,Msis the saturation magnetization,Heffis the effective magnetic field,γis the gyromagnetic ratio andαis the dimensionless Gilbert damping constant. The magnetic parameters of the Py film are chosen asMs=8.0×105A/m, exchange constantA=1.3×10-11J/m, uniaxial anisotropy constantKu= 0 J/m3,α=0.02 in the simulation. The unit cell size of a single ring is set as 5 nm×5 nm×4 nm. To indicate the spatial profiles of resonance amplitude for dynamic magnetization at different fields, the excitation field is applied with sinc function type,H=H0sinc(2π f0(t-t0)), where the amplitudeH0=5 mT,frequencyf0=9 GHz,andt0=1 ns. Then,the magnetization components as a function of time and space are computed by the fast Fourier transform. Therefore, the resonance frequencies of different spin excitation modes can be acquired,as well as the spatial distributions of the fast Fourier transformation amplitude at specific oscillation frequency.

3. Results and discussion

Figure 1 shows the SEM image of sample 4. It can be seen that uniform edges were achieved in most of the rings.The measured diameters of rings are the same as the designed one. For convenient description,we will use the designed size to represent the samples in the following text.

Fig.1.Scanning electron micrograph of permalloy ring arrays with the inner diameter of 25 μm.

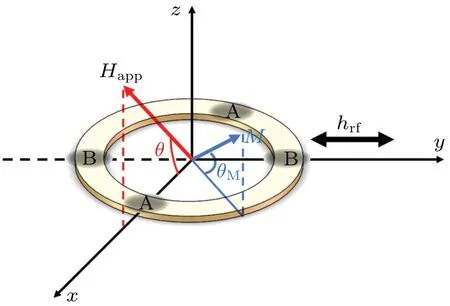
Fig. 2. The coordinate system used for the measurement and analysis of FMR,and the spatial relationship between Happ, hrf, and M. The sample lies in the xy-plane.

Figure 2 shows the coordinate system used to analyze FMR results.Happandhrfare the applied DC and microwave magnetic fields, respectively.θis the angle betweenHappand film plane.θMis the angle betweenMand film plane.Figure 3 shows the in-plane (θ=0) field-swept FMR differential spectra of samples at 9 GHz. As can be seen, high field (HF) mode and low field (LF) mode are observed for sample 1. Similar results were also found in nano-ring magnetic tunnel junction samples, where HF and LF modes were identified as acoustic-like and optical-like fundamental resonance modes,respectively.[16,17]The HF mode exhibits larger intensity. When the inner diameter increased, the HF mode weakened while the LF mode enhanced. Meanwhile,a transition resonance mode is clearly visible between the two modes whend=20 μm. Furthermore,resonance peaks shift slightly with the change ofd. Since all the resonance modes should follow the Kittel equation, this can be explained as the result of spatial variations of demagnetizing fields.

In order to understand how the magnetization state affects resonance spectra, we measured the out-of-plane FMR spectra of samples. Figure 4 shows the FMR spectra of different samples as a function ofθ,which is the angle between film plane and applied magnetic field. The resonance fields would increase when the applied field rotates from the easy axis (in-plane) to the hard axis (out-of-plane). Let us focus on the resonance spectra of sample 1 as shown in Fig. 4(a).Whenθchanged from 2°to 72°,noticeable mutation was not observed no matter in relative intensity or the number of resonance peaks. Whenθchanged from 72°to 81°, two resonance peaks tended to merge into one peak with a relatively larger linewidth. If the magnetic field was close to the perpendicular direction (θ=90°), the resonance peak split into 3 modes in which the intensity increased with magnetic field.For samples 2–4, the similar trend was observed as shown in Figs.4(b)–4(d). That is,resonance peaks gradually merged at lower angle and re-split at higher angle,which happened nearθ=70°,80°. But for sample 3,the transition mode is always visible whenθ ≤80°. To conclude,the resonance modes are divided into three stages with the rise ofθ, and 70°, 80°are two characteristic points of mode evolution.

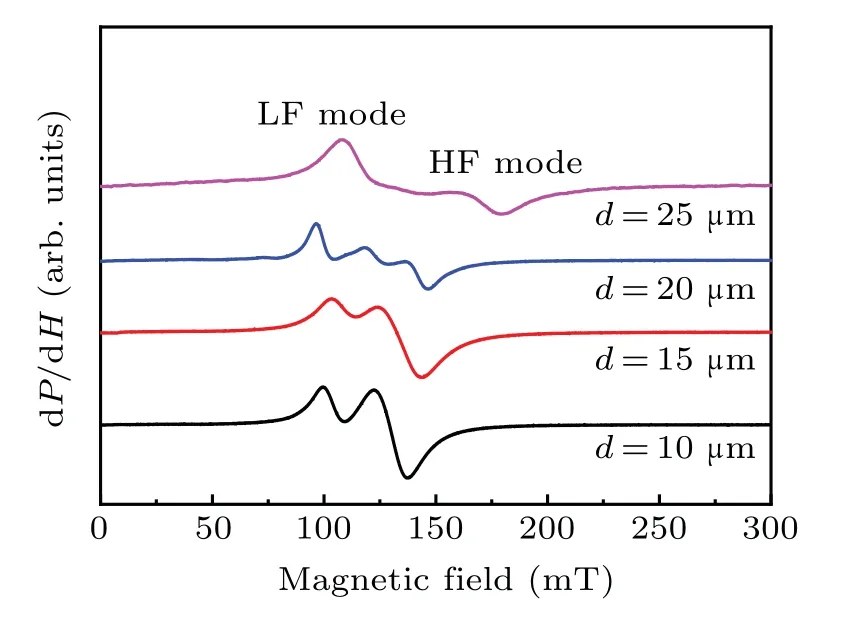
Fig.3. In-plane FMR spectra of samples with different d at 9 GHz.

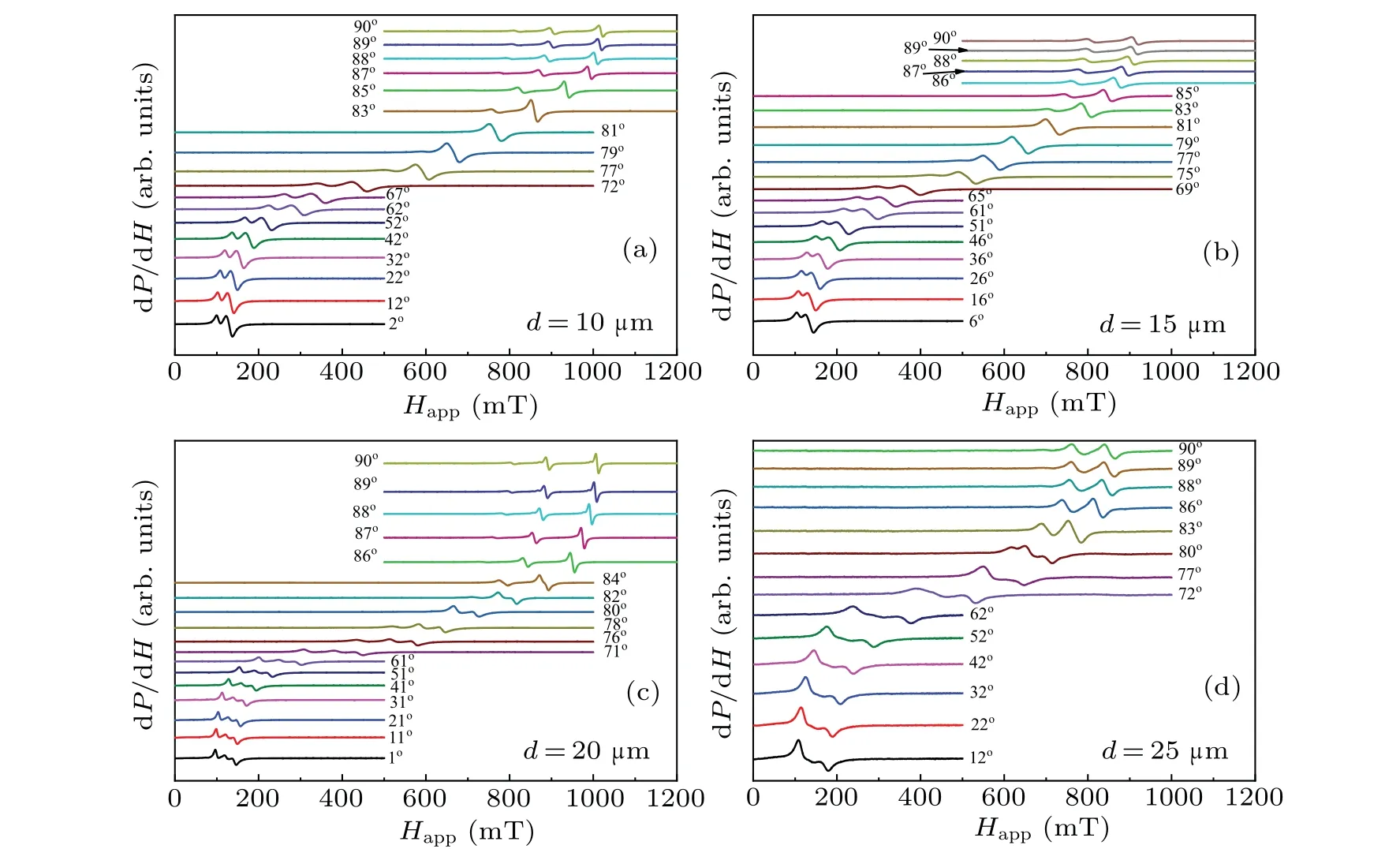
Fig.4. Angle-dependent out-of-plane FMR spectra of samples with different d at 9 GHz. The angle indicated in the figure is the angle between the external magnetic field and the film plane.

Micromagnetic simulation was used to further understand the evolution of resonance modes. Figure 5 shows the simulation results of angle-dependent FMR differential spectra and resonance mode profiles for a Py ring with the size ofD=1200 nm andd=1000 nm. The thickness of the ring is 4 nm. The ratio ofDanddfor simulation item is the same as that of sample 4. DC magnetic field is along thexaxis,and excitation field is along theyaxis. We have selected four characteristic points of 0°, 70°, 80°, and 90°to simulate the actual resonance evolution in the samples. Simulation results show two distinctly different resonance modes when the field is obliquely or horizontally applied on the Py ring. These two resonance modes correspond to LF and HF modes in the experimental results.For LF mode,the magnetization precession mainly occurs in area B,as the gray part shown in Fig.2. For HF modes,multiple resonance peaks are observed. The magnetization precession mainly occurs in area A.The upper parts of Fig.5 show the resonance profiles under different DC magnetic fields,which shows that the multiple HF modes are spin standing waves(SSW)of different orders. For area A,the DC magnetic field is applied along the radial direction of the Py ring. The limited size of radial direction promotes the formation of SSW,which makes multi-order HF modes easier to be observed than the LF mode. High-order HF modes were not observed in the experimental FMR spectra.This may be due to the first-order HF mode with a strong intensity, which makes other high-order signals difficult to be measured. Whenθis 70°and 80°[Figs. 5(b) and 5(c)], the main resonance modes are still LF mode and multi-order HF mode,and the resonance fields of each modes rise slightly. Whenθis 90°[Fig.5(d)],the resonance mode transforms to the PSSW mode.[27]The resonance profiles of the Py ring show that the precession of magnetization occurs throughout the sample instead of local resonance mode.

A distinct difference between experimental and simulation results is the critical angle of mode evolution. For experimental results, as we have pointed out,θ=70°, 80°are two characteristic points. However, whenθ ≤80°, simulation results maintain the similar local resonance mode. Whenθ=90°,the resonance mode of the Py ring changes to PSSW mode of multiple orders,as shown in Fig.5(d). the evolution of resonance modes from local resonance to PSSW probably takes place between 80°and 90°. Because of the different sizes between experimental and simulation samples,the positions of peaks in simulation results would not agree well with the experimental data. Despite this,the simulation results give a reliable evolutionary tendency of the resonance spectra.

To further verify the reliability of simulation results, the Kittel equation is used to analyze resonance field (Hr) as a function ofθ.Considering the geometric structure of Py rings,the demagnetizing fields are important parameters. Based on the coordinate system shown in Fig. 2, the demagnetization factors ofx,yandzdirections are represented asNx,Ny, andNz,respectively.For the HF mode existing in area A,the Kittel equation can be written as[28]

whereωis the angular frequency of the AC excitation field.Also,for the LF mode,

here,θMis the angle between magnetization and film plane.We use Eq. (5) to fit the FMR data. Figure 6 shows the experimental results (dots) and fitting results (lines) ofHras a function ofθ. Obviously,the fitting lines agree well with the experimental results, which strongly verifies our discussion about the evolution of resonance modes. The fitting parameters of all the samples are listed in Table 1. With the rise ofd,Meffgradually decreases, which is due to the reduction ofNz. At the same time,HRdgrows with the rise ofd. In other words,the effective radial demagnetizing field will increase if the ring becomes narrower.

Fig.5. Simulation FMR spectra and the profiles of resonance modes at different resonance fields. The angle between film plane and applied magnetic field is (a) 0°, (b) 70°, (c) 80°, and (d) 90°, respectively. The coordinate system shown in (d) is applicable for all the simulation results,which is the same as Fig.2.

Fig.6. Experimental(dots)and fitting(lines)results of FMR resonance field as a function of θ. (a)d=0 μm;(b)d=15 μm;(c)d=20 μm;(d)d=25 μm.

Table 1. The magnetic parameters obtained from FMR theoretical fitting for all the samples.

Acknowledgement

Project supported by the National Natural Science Foundation of China (Grant Nos. 12074158, 12174166, and 12104197).

4. Conclusions

In summary,the experimental,micromagnetic simulation and mathematical fitting results drew a picture of resonance modes evolution for the Py rings. WhenHappwas applied on the film plane, it would break the original symmetry of Py rings at remanence. Local resonance modes consisting of the high and low field modes occurred at different parts of the rings. The simulation results revealed the existence of high-order high field modes, which were the SSW resonances derived from size limitation. As the magnetic field angle increased, the asymmetry of Py rings gradually disappeared. The high and low field modes merged to a single resonance peak with a relatively larger linewidth. When the magnetic field was applied vertically to the film plane, the multiple resonance peaks shown in the FMR spectra were actually PSSW resonance mode, which was due to the size limitation in the thickness direction of the thin films. Even though multiple peaks were usually measured in the FMR spectra of the magnetic patterned films,which probably possess completely different resonance modes. Our results revealed the evolution of resonance modes at different magnetization state for the Py ring arrays, which is meaningful in designing the microwave and spintronic devices.