LOCALIZED NODAL SOLUTIONS FOR SCHR?DINGER-POISSON SYSTEMS*
Xing WANG (王星) Rui HE (何銳) Xiangqing LIU (劉祥清)
Department of Mathematics,Yunnan Normal University,Kunming 650500,China
E-mail: 1948872435@qq.com;493202750@qq.com;lxq8u8@163.com
Abstract In this paper,we study the existence of localized nodal solutions for Schrdinger-Poisson systems with critical growth We establish,for small ε,the existence of a sequence of localized nodal solutions concentrating near a given local minimum point of the potential function via the perturbation method,and employ some new analytical skills to overcome the obstacles caused by the nonlocal termOur results improve and extend related ones in the literature.
Key words Schrdinger-Poisson systems;localized nodal solutions;perturbation method.
1 Introduction
In this paper,we study the semiclassical states of the Schrdinger-Poisson systems with critical growth
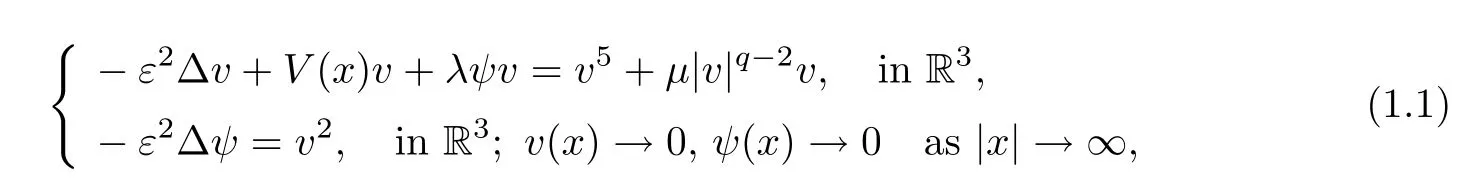
whereε >0 is a small parameter,λ,μ >0.For the potential functionV,we assume that
(V)Vis aC1-function satisfying
(V1) there existc0,c1>0 such that,forx∈R3,c0≤V(x) ≤c1;
(V2) there exists a bounded domainMin R3with smooth boundary?Mand
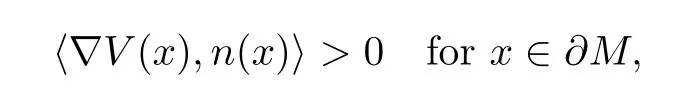
wheren(x) is the outer normal of?Mat a pointx∈?M.
Without loss of generality,we assume that 0 ∈M.Under the assumption (V2),the critical set A ofVcontained inMis a nonempty closed set
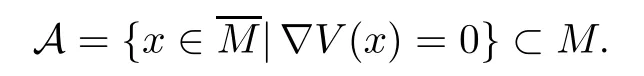
For a setB?R3andδ >0,we denote that
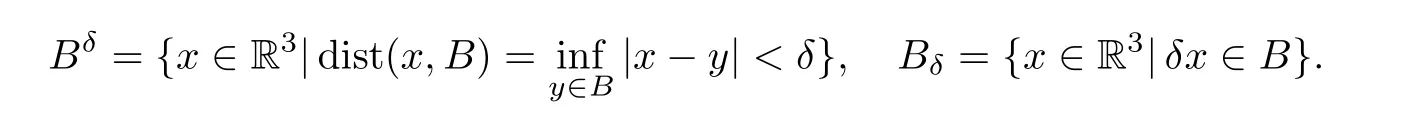
Here is our main result:
Theorem 1.1Assume that 5<q <6 and (V).Then for any positive integerk,there existsεk>0 such that if 0<ε <εk,the problem (1.1) has at leastkpairs of nodal solutions±vj,ε,j=1,2,···,k.Moreover,for anyδ >0,there existα >0,c=ck>0 andεk(δ)>0 such that,if 0<ε <εk(δ),then it holds that
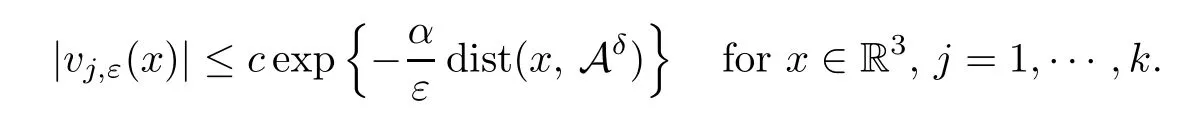
Denoteu(x)=v(εx),φ(x)=ψ(εx).The problem (1.1) reduces to
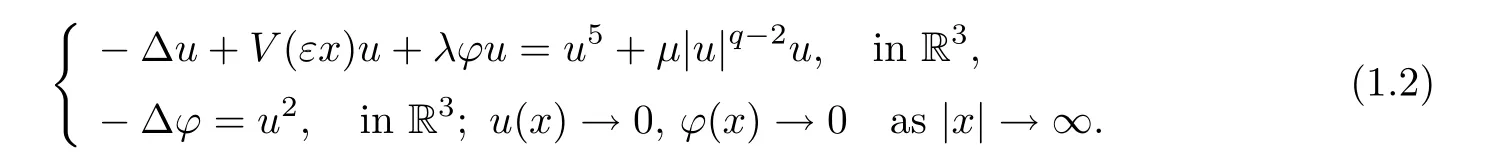
Obviously Theorem 1.1 follows from
Theorem 1.2Assume that 5<q <6 and (V).Then for any positive integerk,there existsεk>0 such that if 0<ε <εk,the problem (1.2) has at leastkpairs of nodal solutions±uj,ε,j=1,2,···,k.Moreover,for anyδ >0,there existα >0,c=ck>0 andεk(δ)>0 such that,if 0<ε <εk(δ),then it holds that
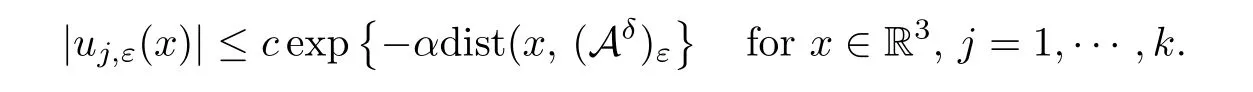
The problem (1.2) has a variational structure given by the functional
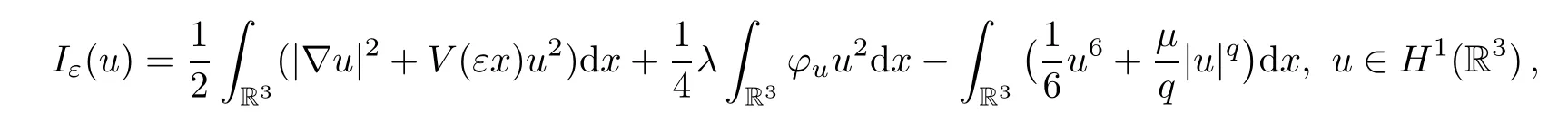
whereφ=φu∈D1,2(R3) is the unique solution of the Poisson equation
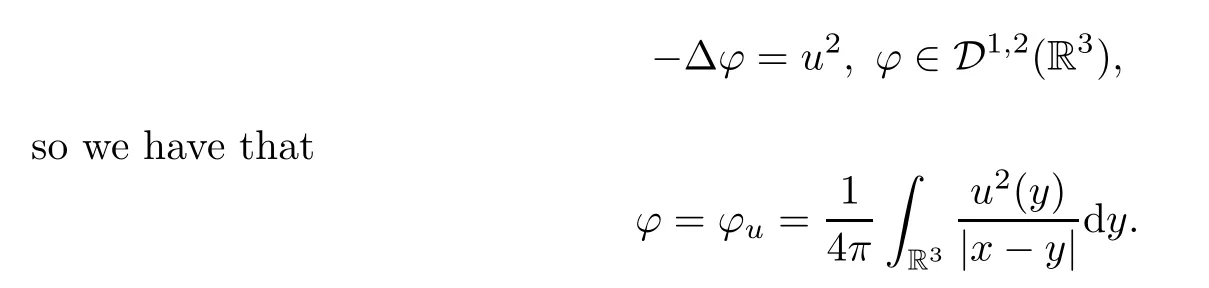
Now we define the perturbation functionals.We need some auxiliary functions.Letξ∈C∞(R,[0,1]) be a smooth,even function such thatξ(t)=1 for |t| ≤1,ξ(t)=0 for |t| ≥2 and-2 ≤ξ′(t) ≤0 fort≥0.Forε,ν∈(0,1],x∈R3,z∈R,define
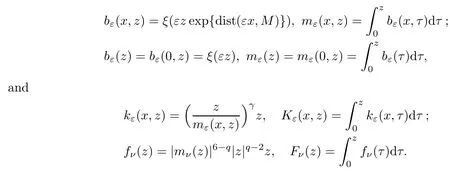
Letζ∈C∞(R) be a smooth function such thatζ(t)=0 fort≤0,ζ(t)=1 fort≥1 and 0 ≤ζ′(t) ≤2.Define
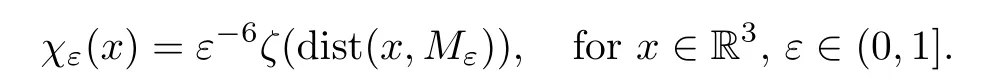
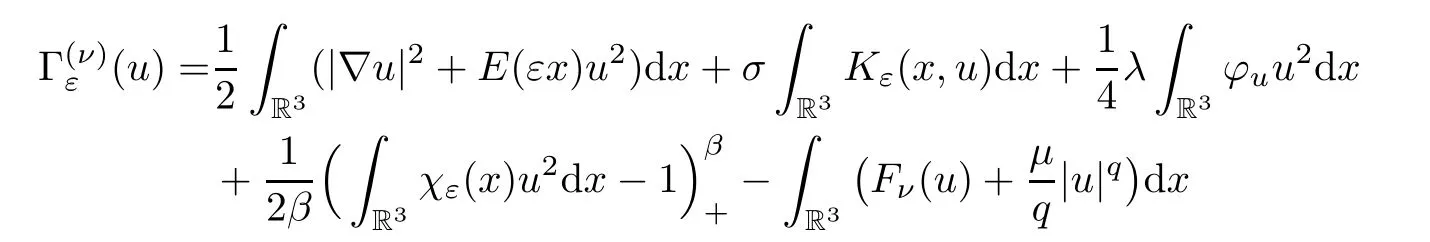
foru∈,whereε,ν∈(0,1],2<2β <q,4<2 +γ <q,E(x)=V(x) -σandσ >0 is small so thatEsatisfies the assumption (V)(with a different constant),andis a weighted space defined as
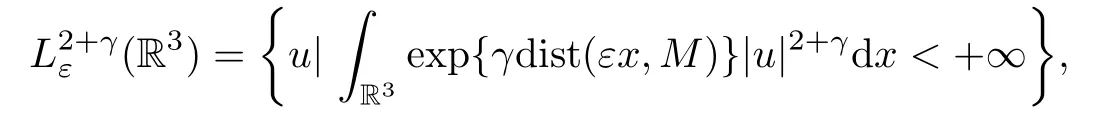
endowed with the norm
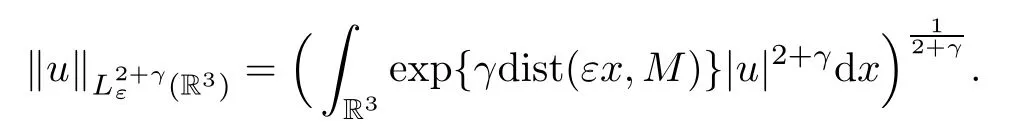
Lettingu∈Xεbe a critical point of,
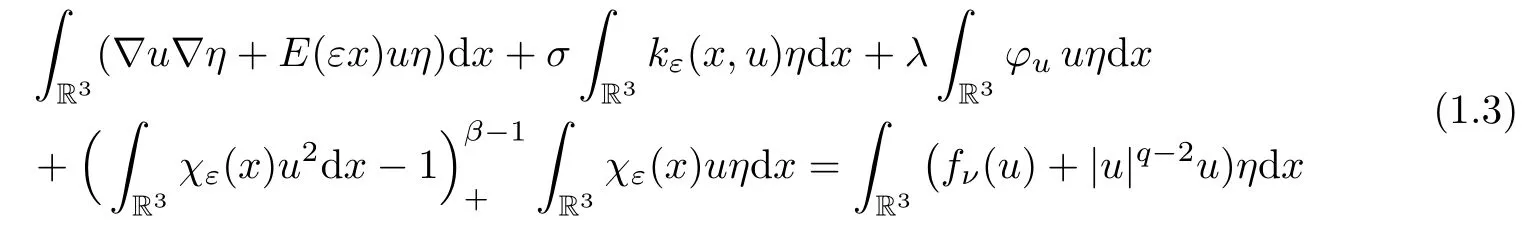
forη∈Xε.Notice that the perturbed nonlinear termfνis of subcritical growth.Since the spaceXεis compactly imbedded intoLp(R3)(1 ≤p <6)(see Lemma 2.2),the functionalsatisfies the Palais-Smale condition.We construct a sequence of nodal critical points of the functionalby using the method of invariant sets with descending flow (see [1]).Now suppose that we have a “good” estimate on the solutionuof (1.3),that is,
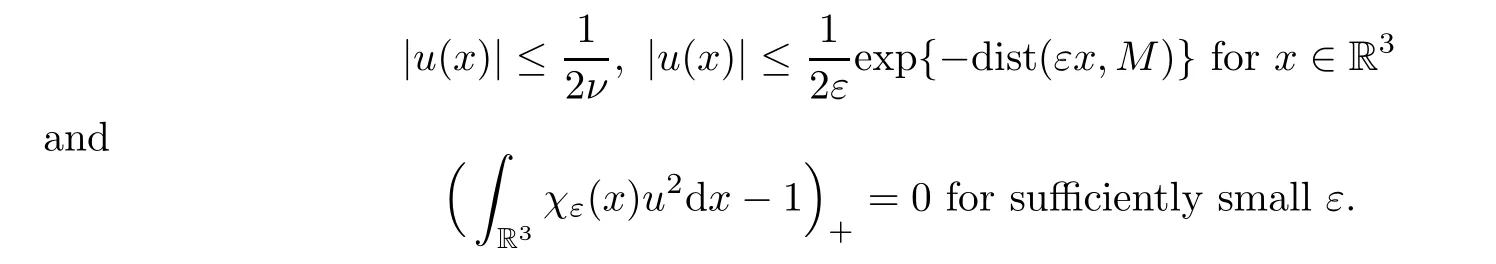
Thenuwill be a solution of the problem (1.2) and localized near the critical set A.
The paper is organized as follows: in Section 2 we prove preliminary results and verify the Palais-Smale condition for the functional.In Section 3 we construct a sequence of nodal critical points ofby using the invariant sets method.In Section 4 we prove our main theorems based on uniform bounds on the critical points obtained in Section 3.
Throughout this paper,we usecto denote different constants,and we use →and?to denote the strong convergence and the weak convergence in a given space,respectively.
2 Preliminary Results
In this section we collect elementary results about the auxiliary functions used to define the perturbed functional,and we prove that the functionalsatisfies the Palais-Smale condition.
Lemma 2.1Forx∈R3,z,w∈R,it holds that
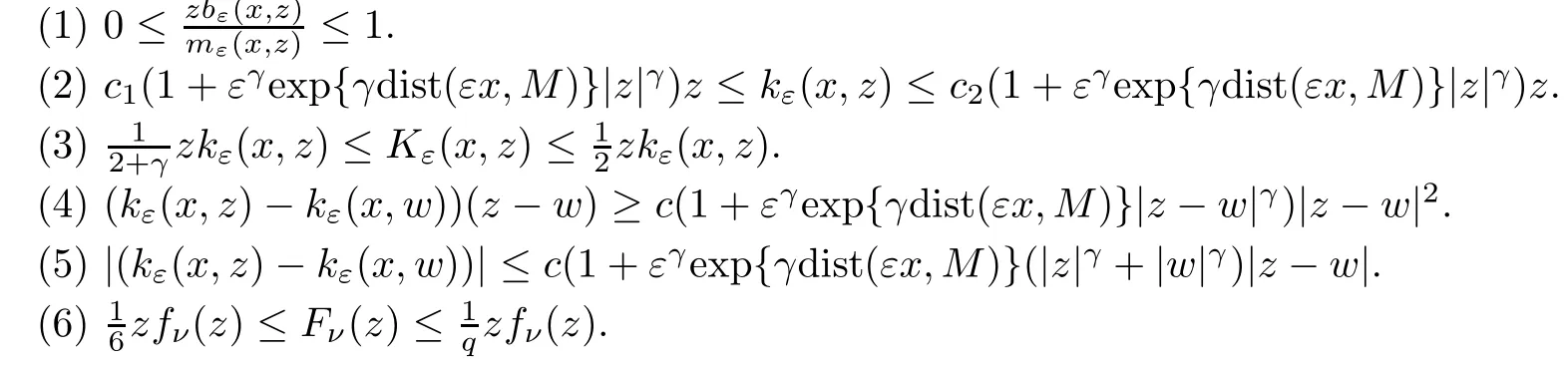
ProofThe proof is straightforward.We prove (3).
(3) Forz >0,mε(x,z) is increasing inz,sois decreasing inzand forz >0.Consequently,forz∈R
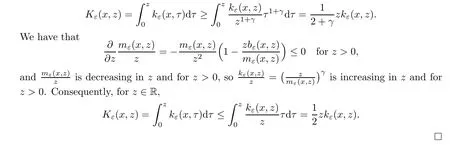
Lemma 2.2The imbeddingis compact for 1 ≤p <6.
ProofLet {un} be bounded inXε,and assume thatun?uinXεand thatun→uin,with 1 ≤p <6.We first proveun→uinL1(R3).ForR >0,we have that
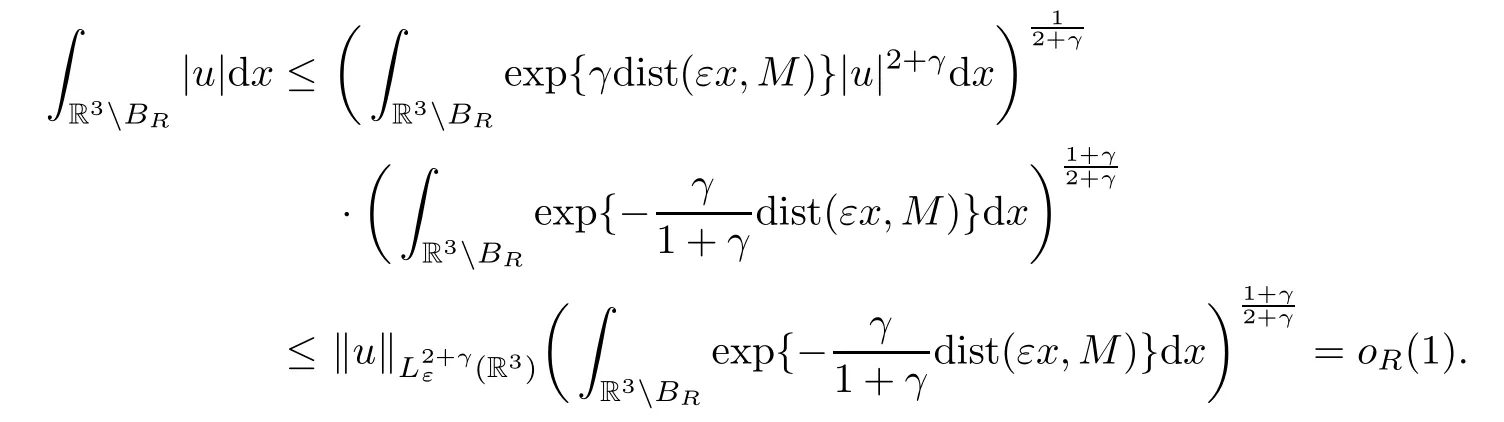
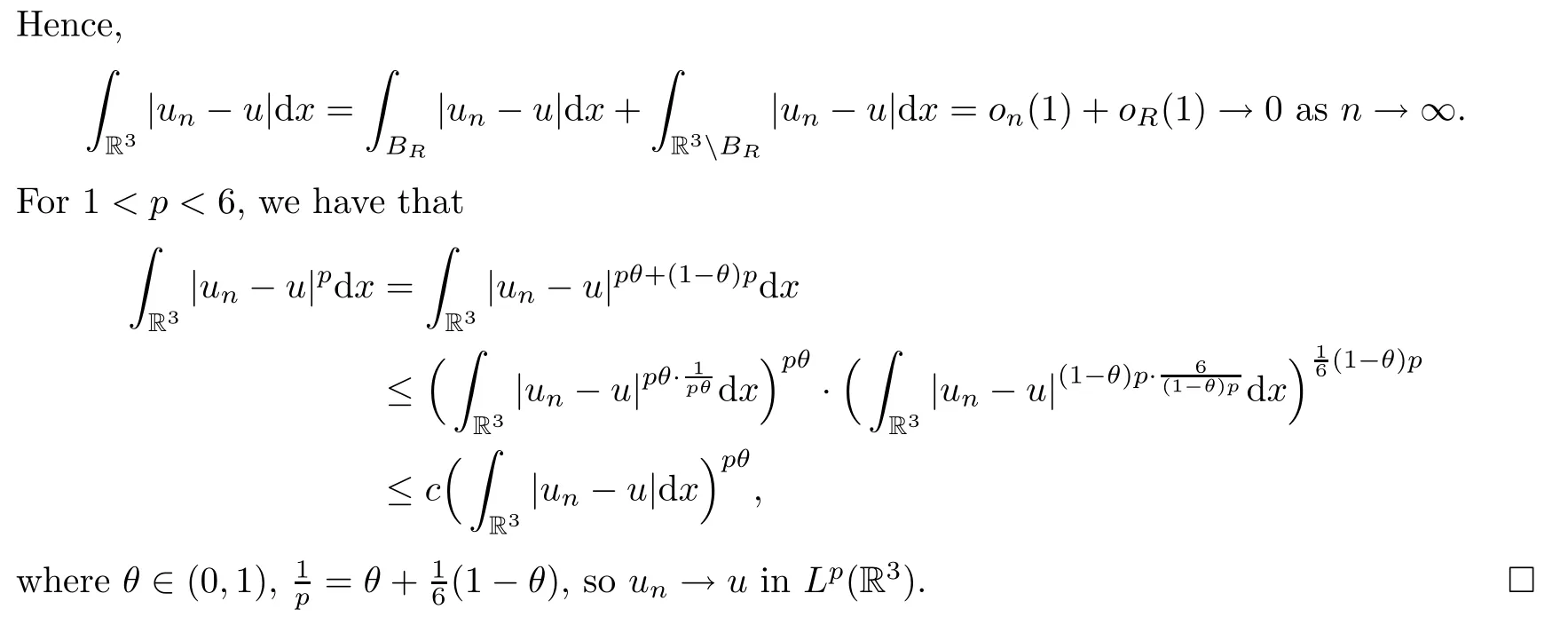
Considering the Poisson equation
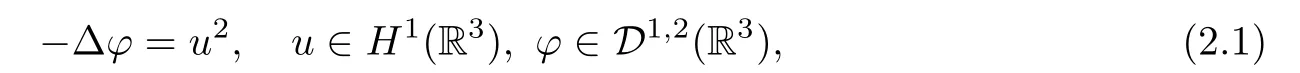
φ=φucan be expressed as
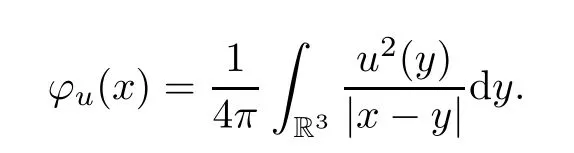
The functionφuhas the following properties (see [7,8]):
Lemma 2.3Foru∈H1(R3),it holds that
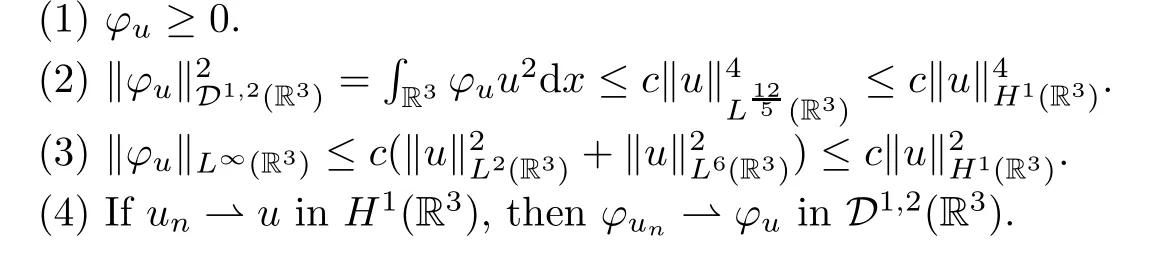
Proof(1) It is obvious.
(2) By the equation (2.1) and Sobolev’s inequality,
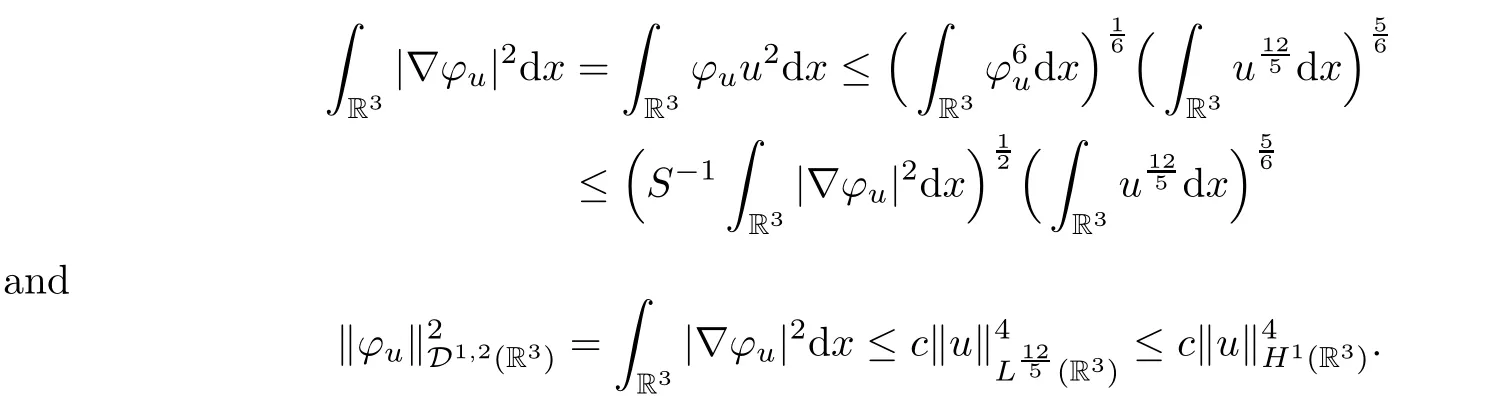
Noticing that
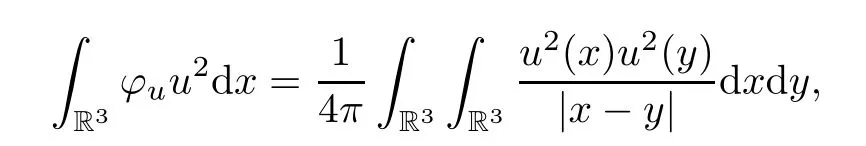
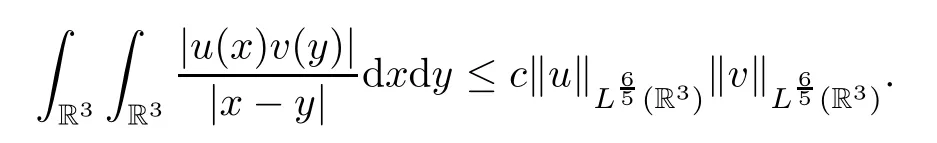
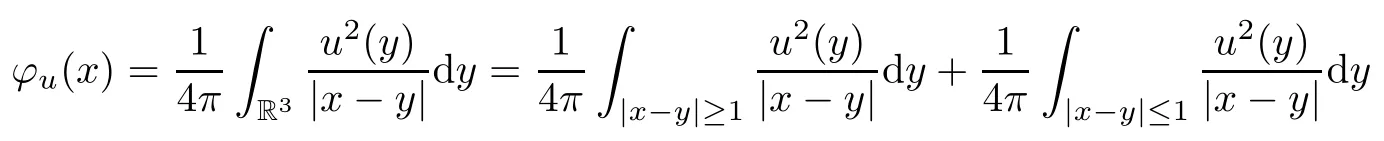
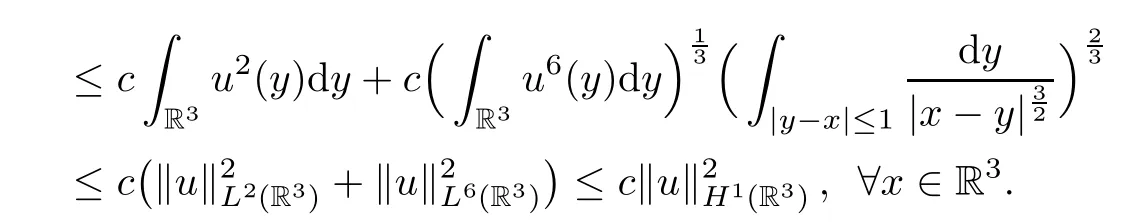
(4) Assume thatun?uinH1(R3).Thenφunis bounded in D1,2(R3).Assuming thatφun?φin D1,2(R3),we obtain that
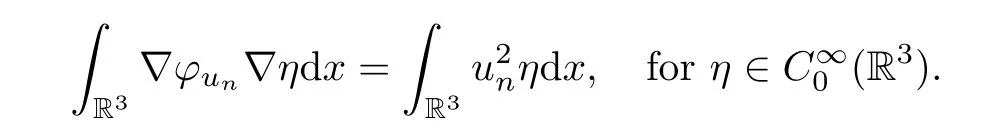
Taking the limitn→∞,we obtain that

hence,φ=φu;that is,φun?φuin D1,2(R3). □
Lemma 2.4Let {un} be a Palais-Smale sequence of the functional.Then {un} is bounded inXε.
ProofWe have that
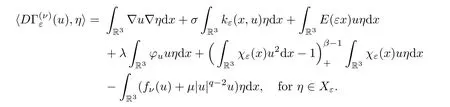
By Lemma 2.1 and Lemma 2.3,we have that
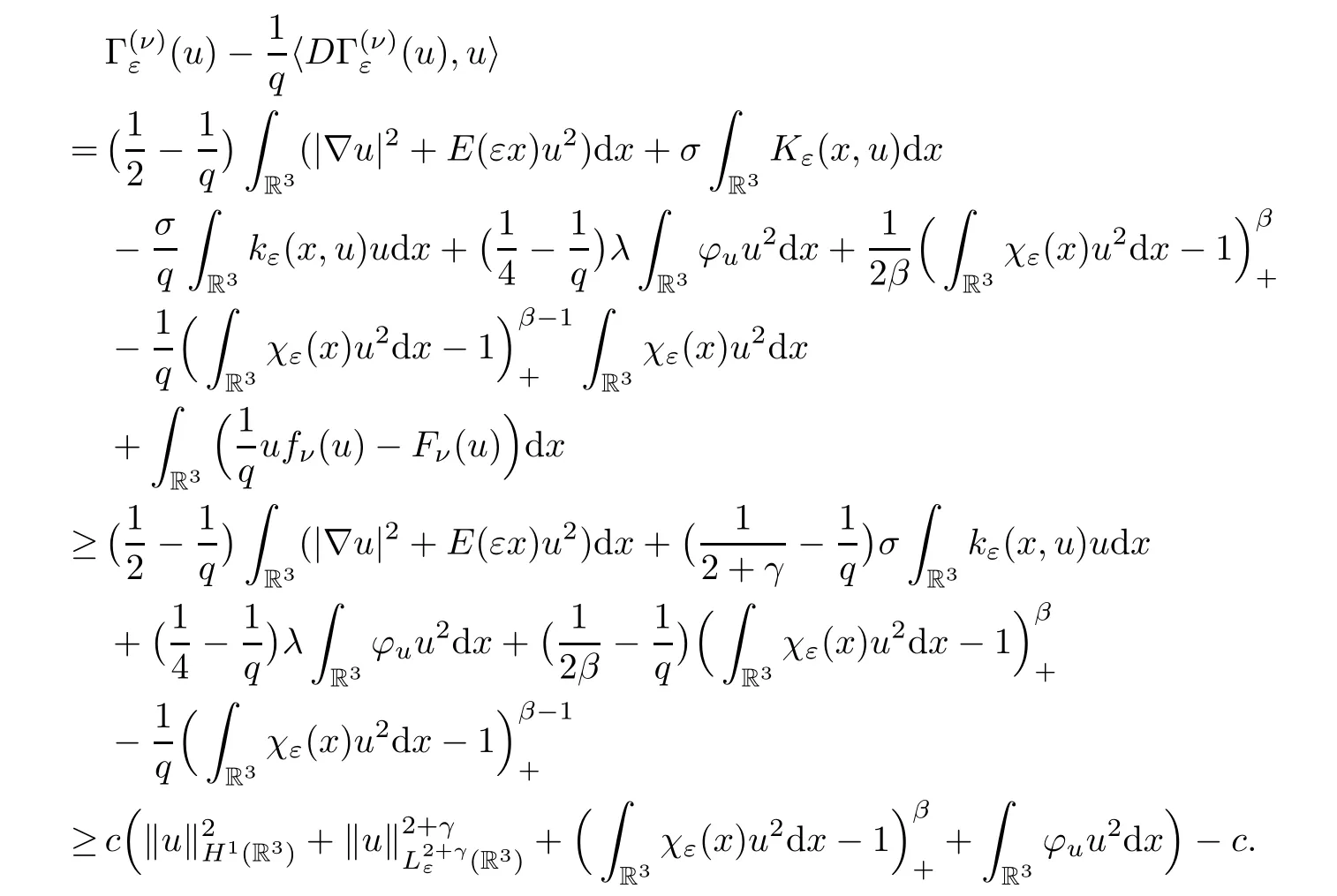
Hence any Palais-Smale sequence is bounded inXε. □
Lemma 2.5satisfies the Palais-Smale condition.
ProofLet {un} be a Palais-Smale sequence of the functional.By Lemma 2.4,{un}is bounded inXε,so by Lemma 2.2,we can assume thatun→uinLp(R3)(1 ≤p <6).By Lemma 2.1 and Lemma 2.3,we get that

Then {un} is a Cauchy sequence inXε. □
3 Critical Points of the Functional Γ
In this section we construct a sequence of nodal critical points of the perturbed functionalby using the method of invariant sets with respect to descending flow.First we define an operatorA:Xε→Xε;the vector fieldu-Auwill be used as pseudo-gradient vector field of the functional.
Definition 3.1Givenu∈Xε,definev=Auby the following equation:
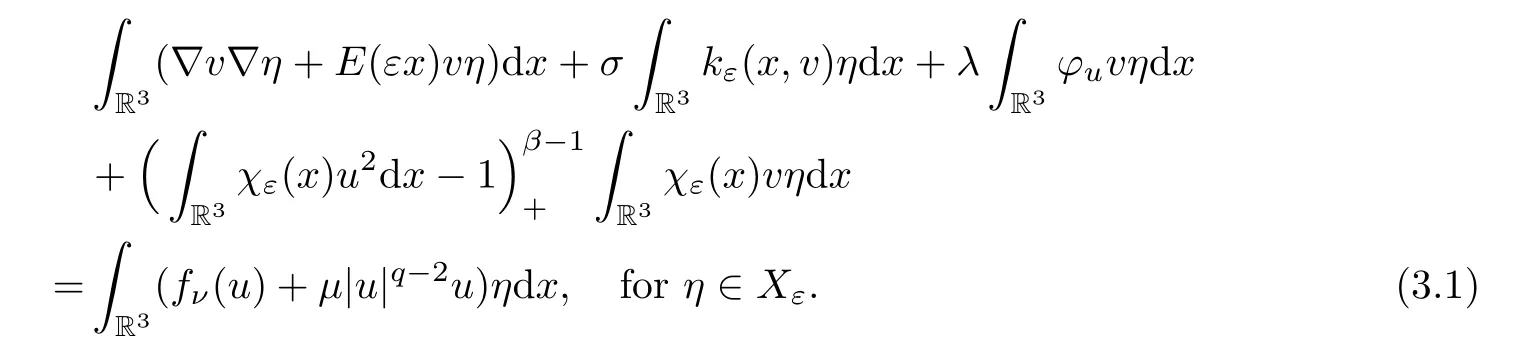
Lemma 3.2The operatorAis well-defined and continuous.
ProofDenote that

forη∈Xε.The operatorB:v∈Xε→B(v) ∈X*εis strongly monotone.In fact,
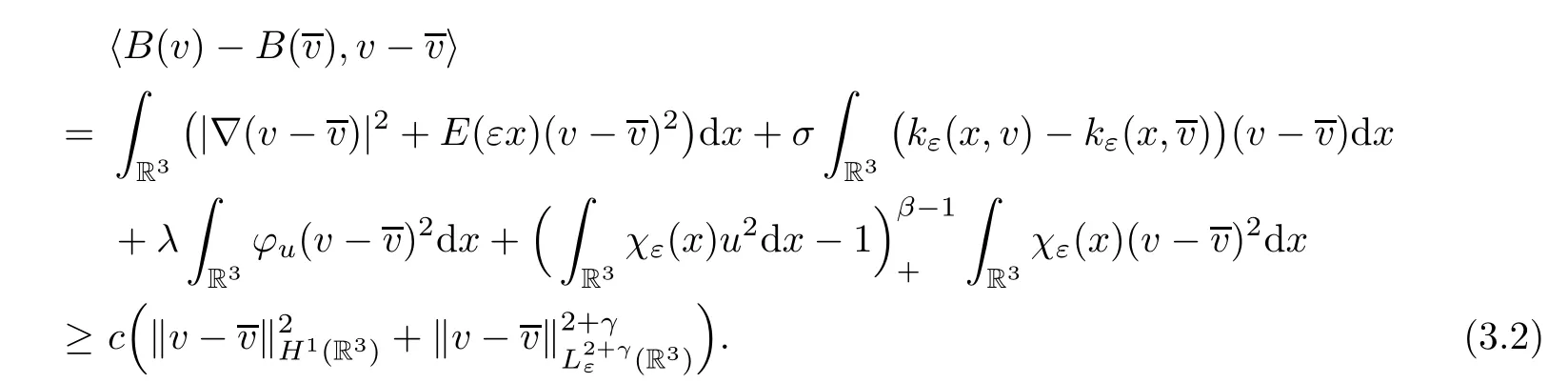
Hence the equation (3.1) has a unique solution:v=Au.Assume that∈Xε,v==.Then
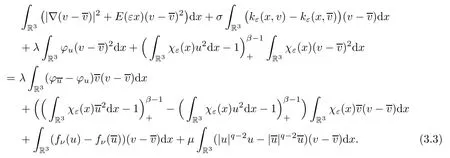
The right hand side of (3.3) is
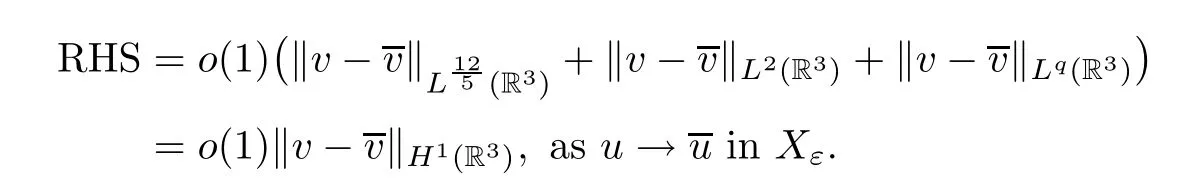
The left hand side of (3.3) is
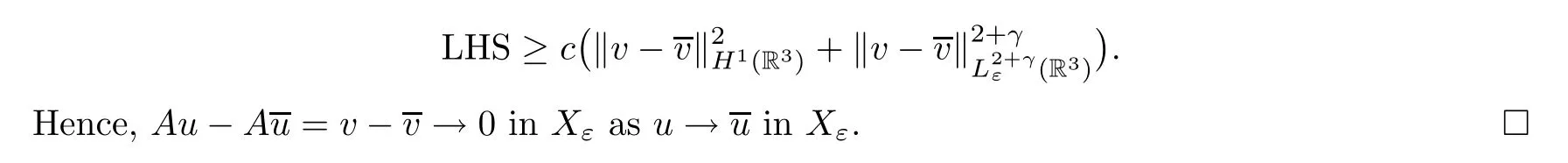
Lemma 3.3There exist constantsd,c,α >0 such that
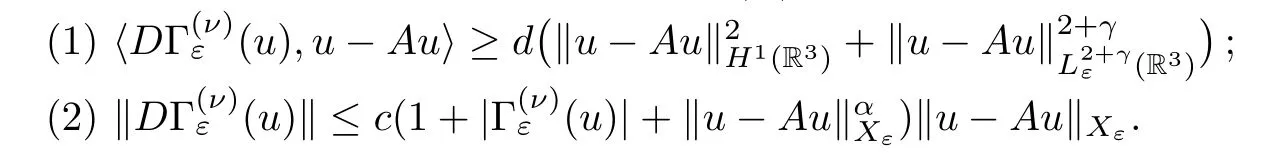
Proof(1) By the definition of the operatorA,we have that
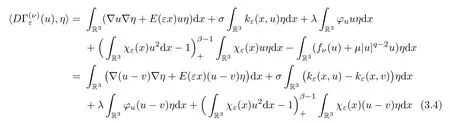
forη∈Xε.Hence
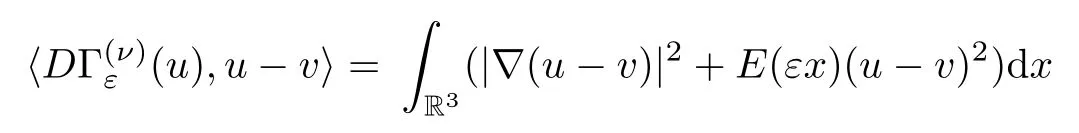
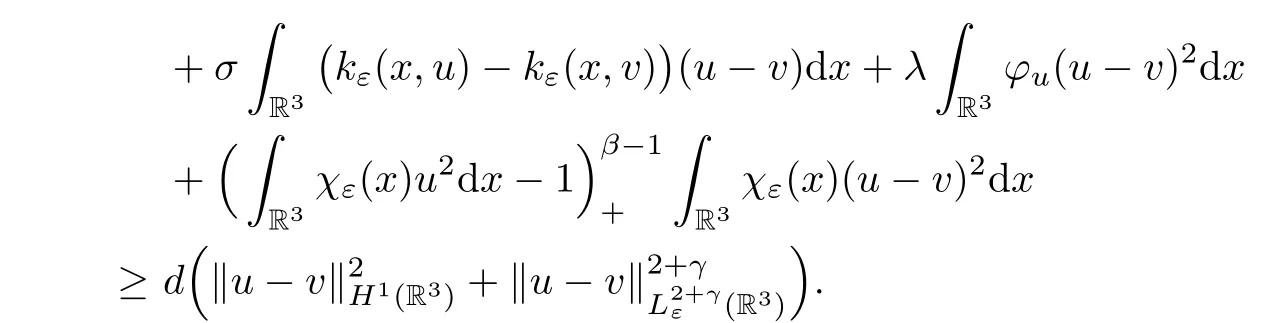
(2) By (3.4),we have that
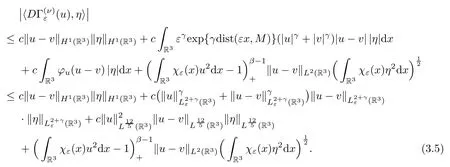
In the above we have used the estimate
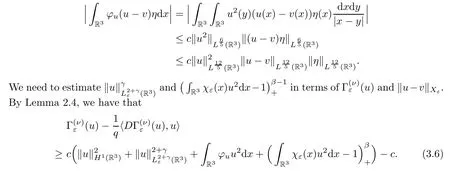
The left hand side of (3.6) is
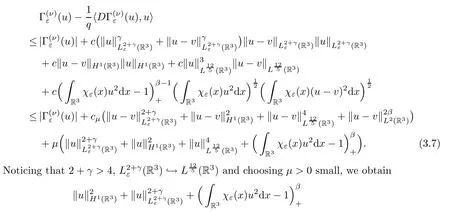
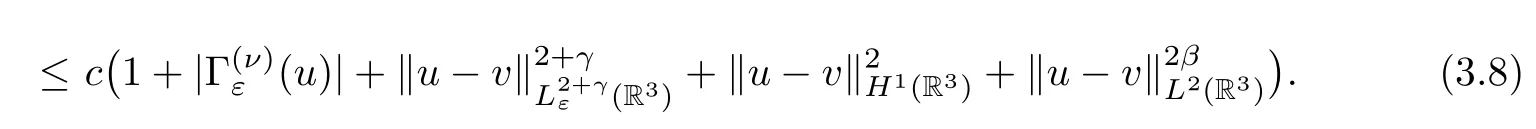
By (3.5) and (3.8),we obtain that
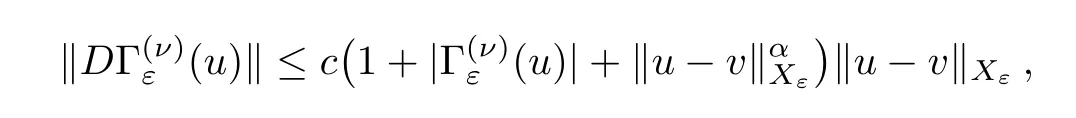
whereα=max{2 +γ,2,2β}. □
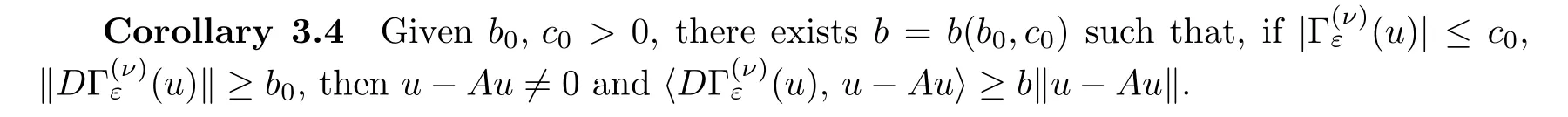
Now we define the convex open setsPandQ:
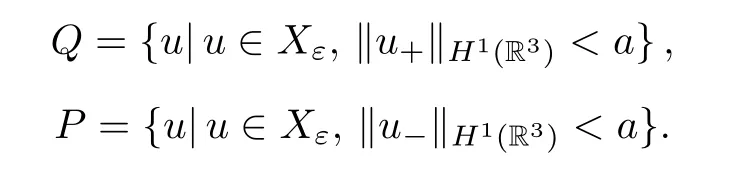
Hereais a positive constant.
Lemma 3.5There existsa0>0 such that,for 0<a <a0,A(?Q) ?Q,A(?P) ?P.
ProofGivenu∈Xε,denote thatv=Au,vsatisfies the equation (3.1);that is
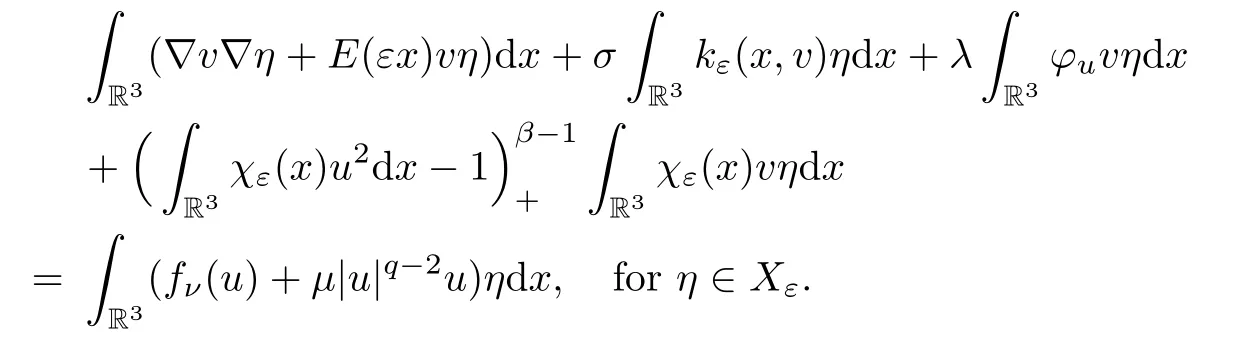
Takingη=v+as a test function,we have that
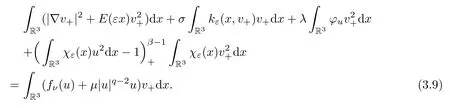
We estimate the left hand side of (3.9) as

whered0is a positive constant.The right hand side of (3.9) is
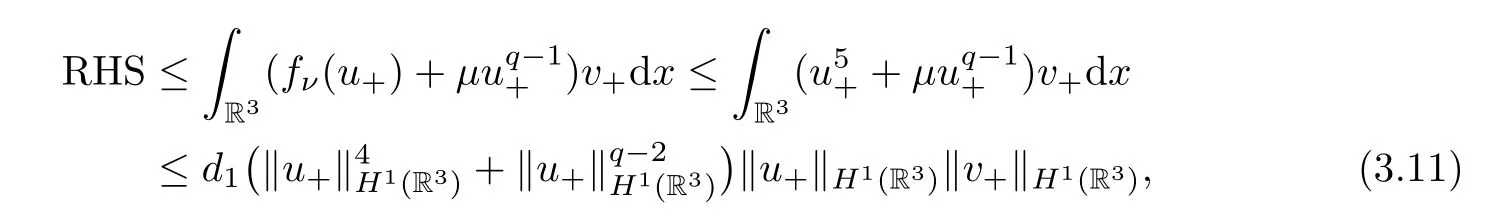
whered1is a constant.Choosea0such that
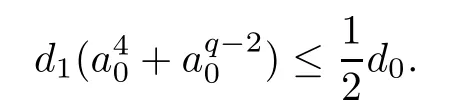
Then,for 0<a <a0,u∈?Q,‖u+‖H1(R3)=a,we have that
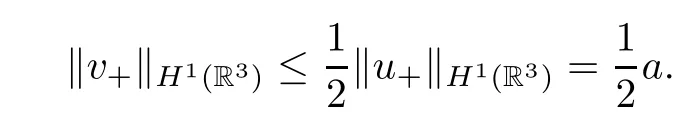
Hence,v∈Q;that isA(?Q) ?Q.Similarly,A(?P) ?P. □
Lemma 3.6There existsa0>0 such that,for 0<a <a0,
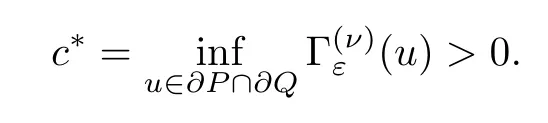
ProofForu∈?P∩?Q,we have that
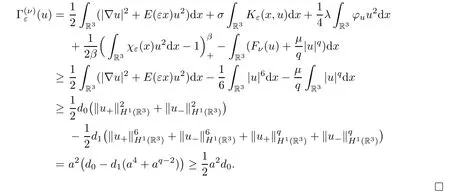
In summary,we have defined the functional,the odd mapA:Xε→Xε,the convex open setsPandQ,and have verified that
(I1)is aC1-functional and satisfies the Palais-Smale condition (Lemma 2.5);
(I2)(u)>0 (Lemma 3.6);
(A1) givenc0,b0>0,there existsb=b(c0,b0)>0 such that,ifthenu-Au0 and≥b‖u-Au‖ (Corollary 3.4);
(A2)A(?P) ?P,A(?Q) ?Q(Lemma 3.5).
Now we define the sequence of critical values of
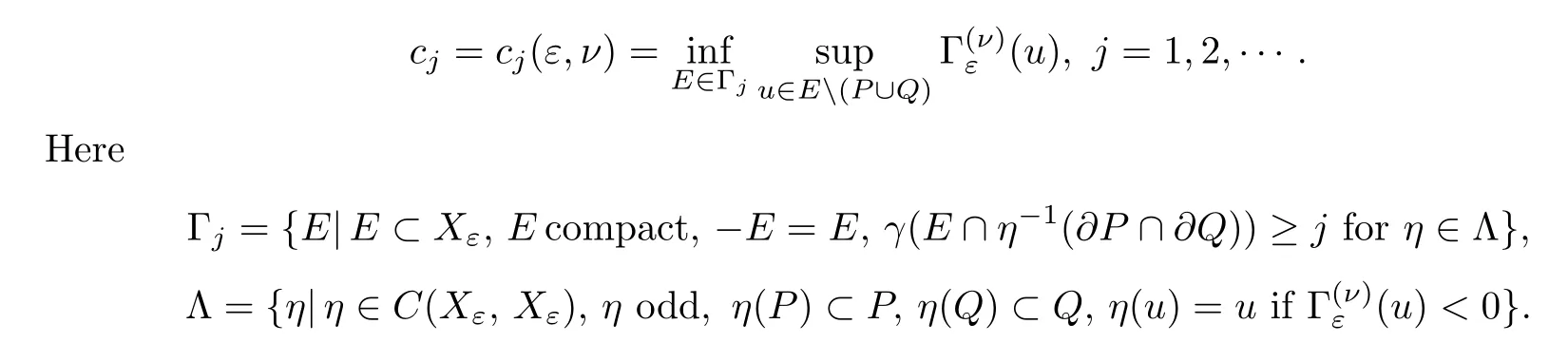
Lemma 3.7Γjis nonempty,j=1,2,···.
ProofAssume thatB={x∈R3||x| ≤r} ?M.Letting {en}∞n=1be a family of linearly independent functions inC∞0(B),then there exists an increasing sequence {Rn} such that
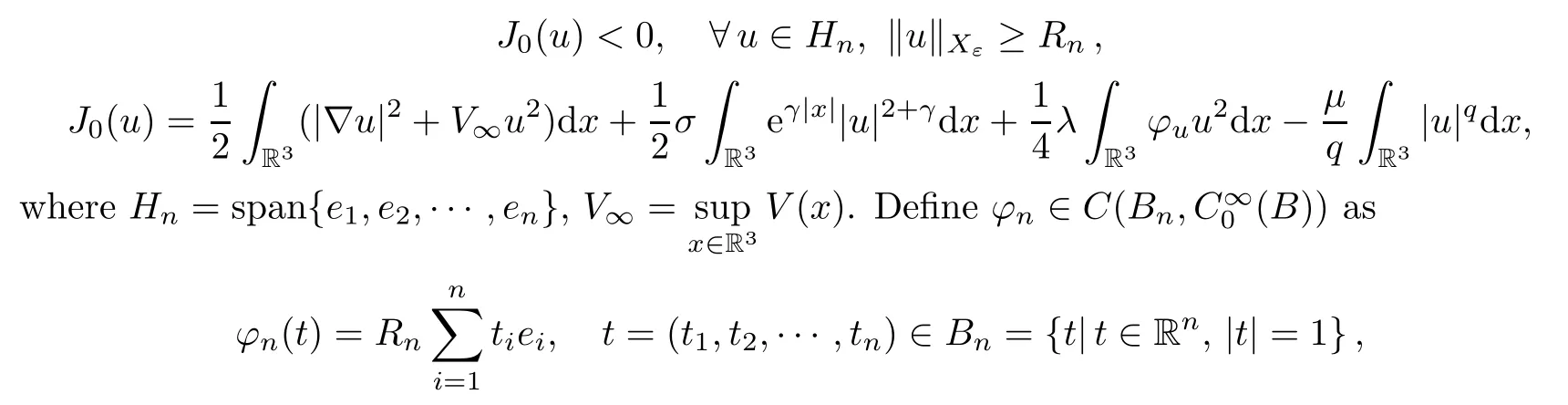
whereRnis chosen so that ‖φn(t)‖Xε≥Rnfort∈?Bn.By Lemma 5.6 in [12],we have thatEj=φj+1(Bj+1) ∈Γj,j=1,2,···. □
We are now in a position to prove the following proposition:
Proposition 3.8The functionalhas a sequence of nodal critical points ±uj,ε,j=1,2,··· satisfying that
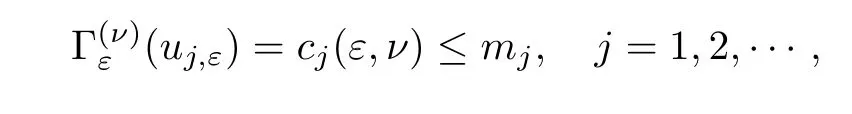
wheremjis independent ofν,ε,j=1,2,···.
The assumptions (I1),(I2),(A1),(A2) and (Γ) hold.Apply the abstract theorem (see [12,Theorem 4.1]),we conclude that
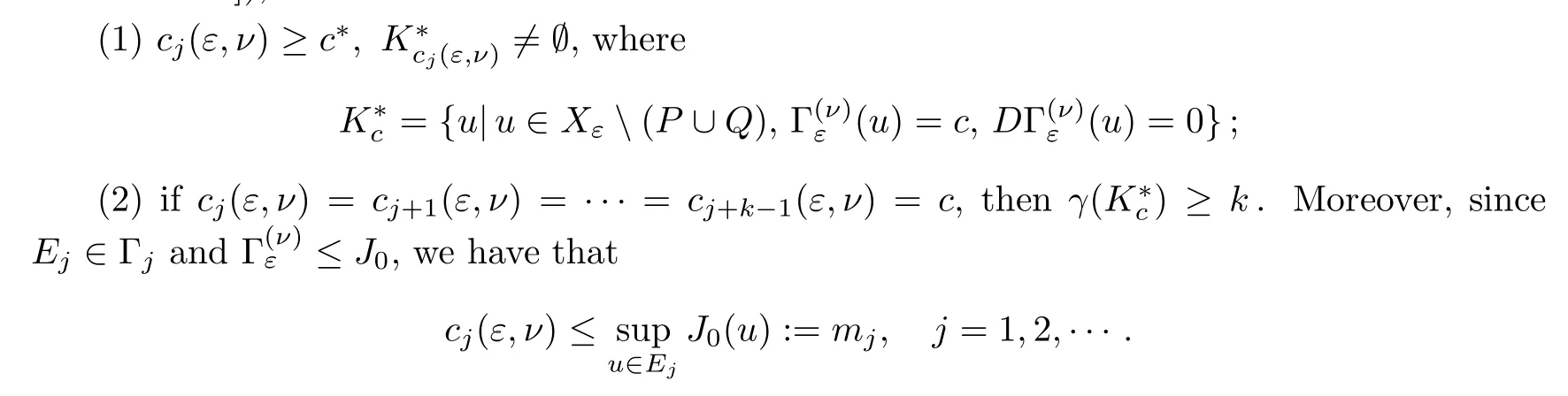
4 The Proof of Theorem 1.2
In this section we prove that the critical points of the functionalobtained in Section 3 satisfy some uniform bounds,and consequently,for a suitable choice ofνthese critical points are also critical points of the functionalIε,that is,solutions of our original problem.
Aside from the functionalIεand,we introduce another perturbed functional:
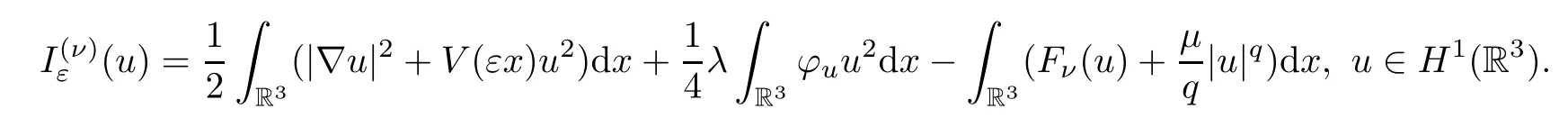
We have the following uniform bounds:
Proposition 4.1Givenν∈(0,1],L >0,assumeu∈Xε,Then there exist positive constantsα,cindependent ofεsuch that,for anyδ >0,there existsε(δ)>0 such that,for 0<ε <ε(δ),
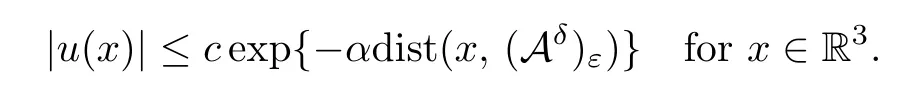
Proposition 4.2Assume thatL >0,u∈H1(R3),Then there exists a positive constantMindependent ofν,εsuch that
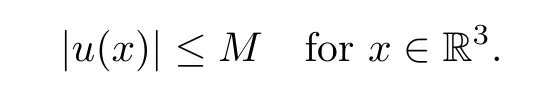
Proof of Theorem 1.2Given a positive integerk,by Proposition 3.8,the functional,ν,ε∈(0,1] haskpairs of nodal critical points ±uj,ε,j=1,···,k,and the corresponding critical values satisfy
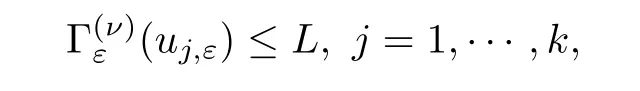
whereLis independent ofν,ε.
Assume thatu∈H1(R3),.By Proposition 4.2,there exists a positive constantM,independent ofν,ε,such that
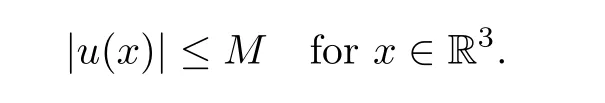
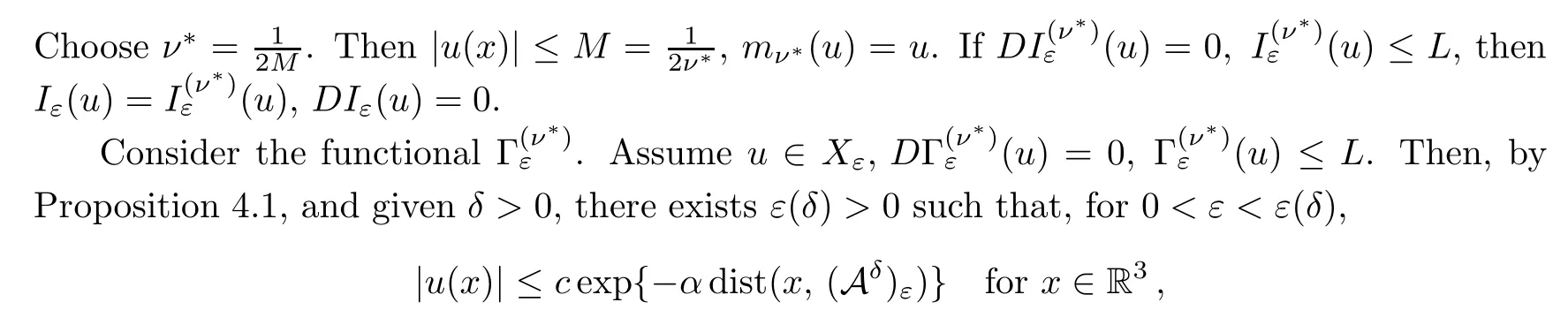
wherec,αare independent ofε.Assume that.Then,for 0<ε <ε(δ),
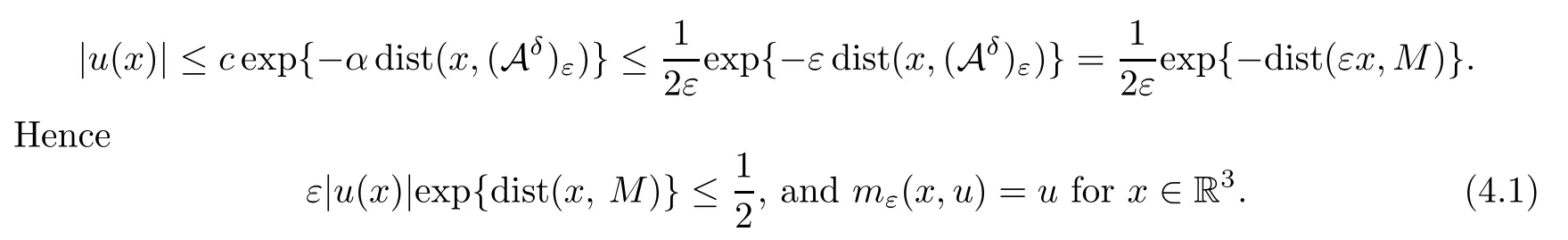
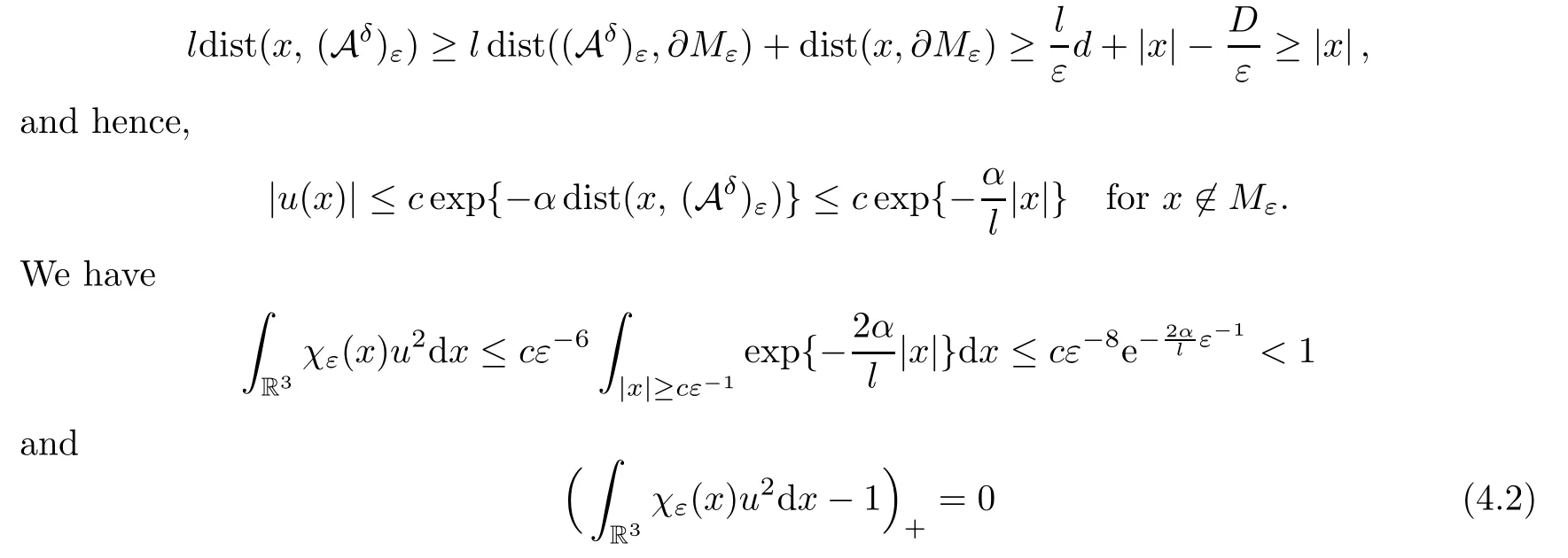
forε <ε(δ) sufficiently small.It follows from (4.1) and (4.2) that
In summary,given a positive integerk,by Proposition 3.8,we obtainkpairs of nodal critical points ±u1,ε,···,±uk,εof the functionalsatisfying
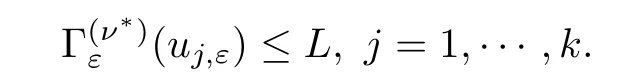
Givenδ >0 there existsε(δ) such that,forε≤ε(δ),uj,ε,j=1,···,ksatisfy
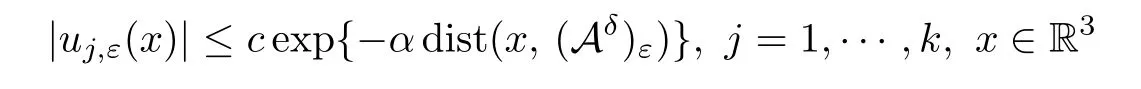
andIε(uj) ≤L,DIε(uj)=0.Hence
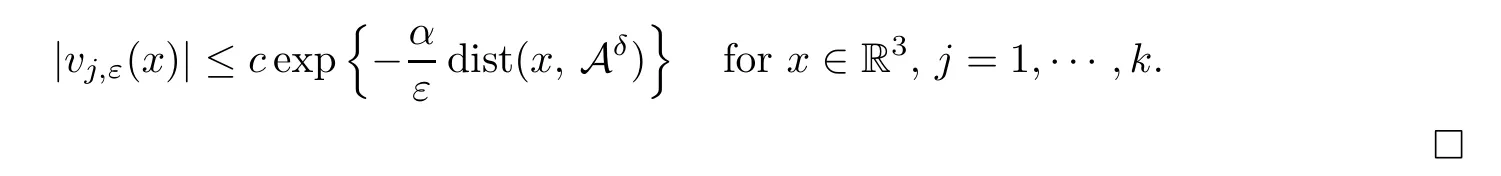
5 Uniform Bounds
In this section we prove Propositions 4.1 and 4.2.The main ingredients of the proof are the profile decomposition of the bounded sequence of the Hilbert space and the local Pohoaev equality.In this section the parameterνis fixed.
Lemma 5.1Assume thatu∈Xε,L >0,.Thenuis bounded inXε.
ProofSee Lemma 2.4. □
Lemma 5.2Assume thatu∈Xε,L >0,.Then there existsKindependent ofεsuch that |u(x)| ≤Kforx∈R3.Moreover,for anyδ >0,there existsc=c(δ) independent ofεsuch that |u(x)| ≤cε3forx∈R3(Mε)δ.
ProofIt is by Moser’s iteration.
(1) Fork≥1,T >0,letuT(x)=u(x) if |u(x)| ≤T,anduT(x)=±Tif ±u(x) ≥T.Chooseη=|uT|2k-2uas test function in.Then we have that
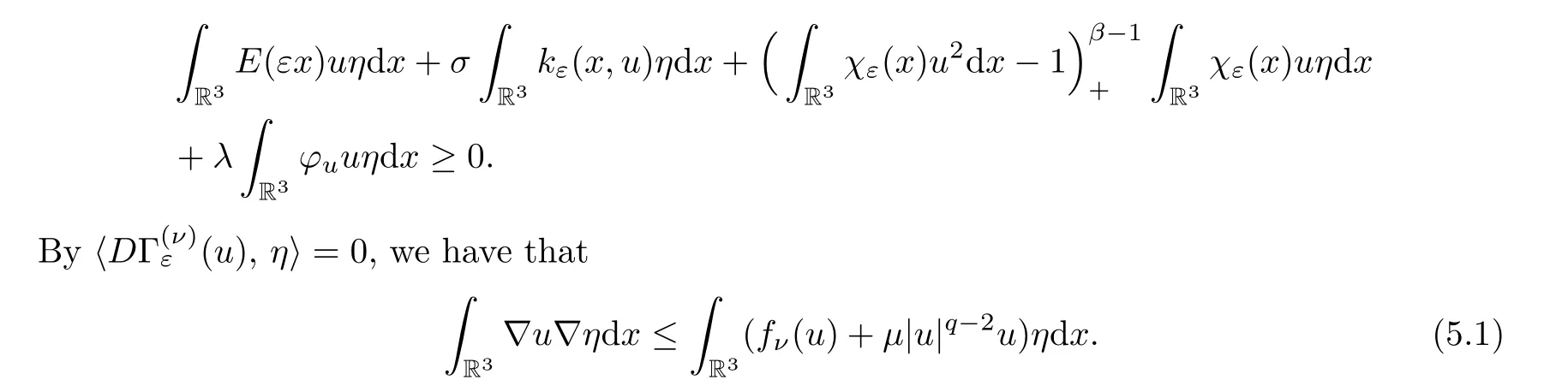
First,we estimate the right hand side of (5.1).Sinceνis fixed,|fν(z)|=|mν(z)|6-q|z|q-1≤cνq-6|z|q-1,so
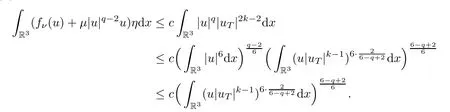
The left hand side of (5.1) is
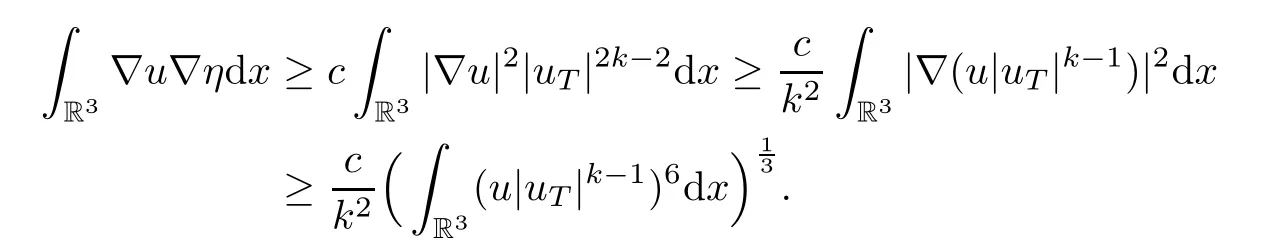
Thus,by (5.1),we have that
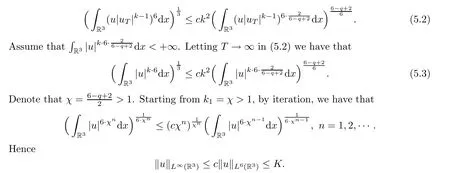
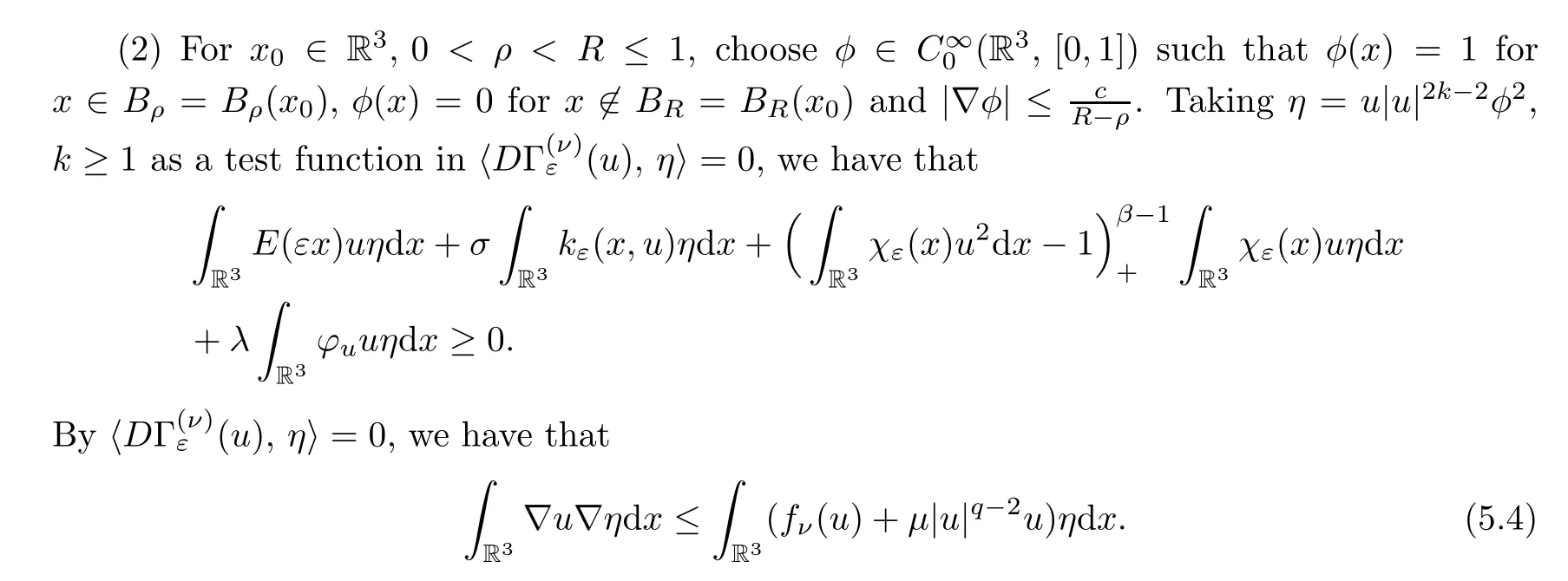
We estimate the left hand side of (5.4) as
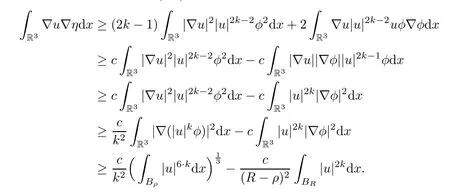
The right hand side of (5.4) is
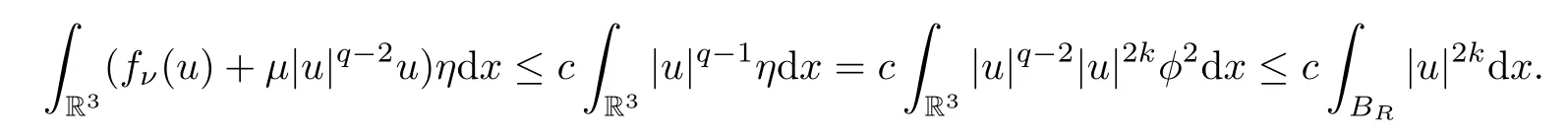
Then we have that
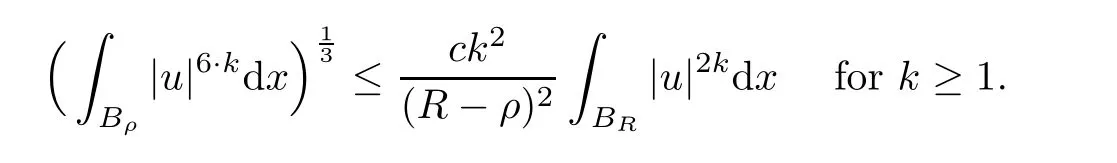
By iteration,we get that
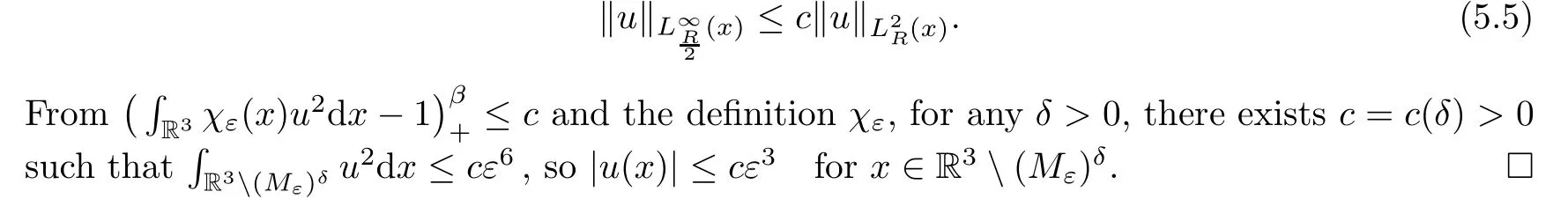
Now we assume thatεn→0,un∈Xεn,L >0,.By Lemma 5.1,unis bounded inH1(R3).The following profile decomposition holds (see[14]):
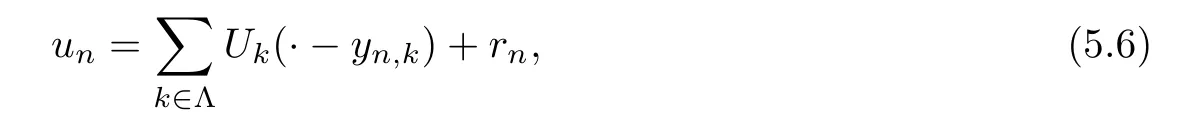
where Λ is an index set,yn,k∈R3,andUk,rn∈H1(R3),satisfying that
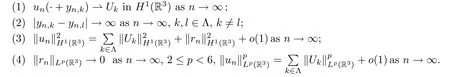
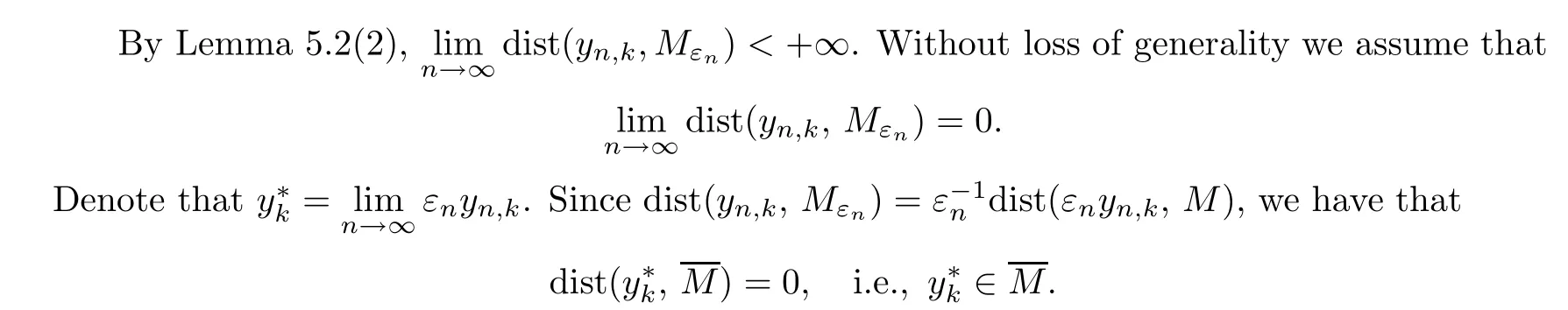
Lemma 5.3Assume thatyn∈R3,wn=un(· +yn)?UinH1(R3).ThenZ=|U|satisfies that
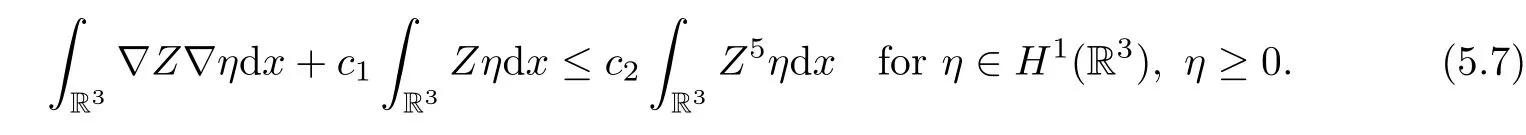
ProofBy Kato’s Lemma,zn=|un(·)| satisfies that
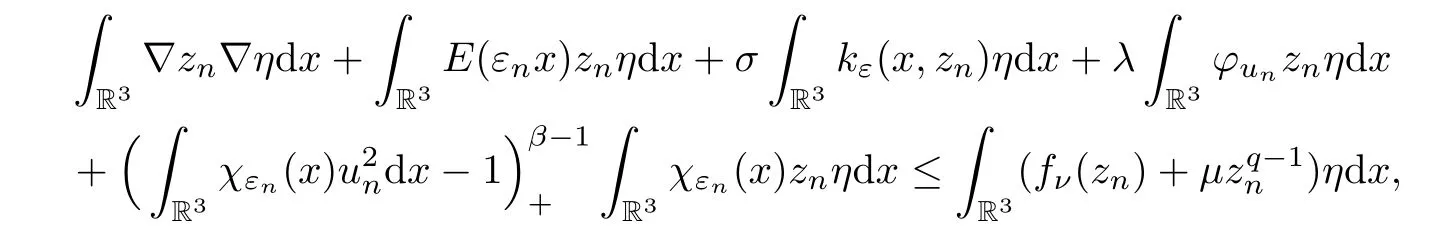
forη∈H1(R3),η≥0.Noticing thatkε(x,zn) ≥zn,φun≥0,fν(zn) ≤we have that
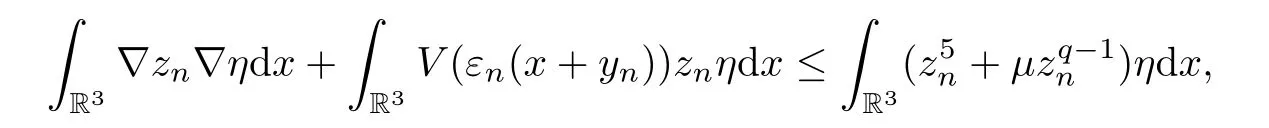
forη∈H1(R3),η≥0.Choose constantsc1,c2such that
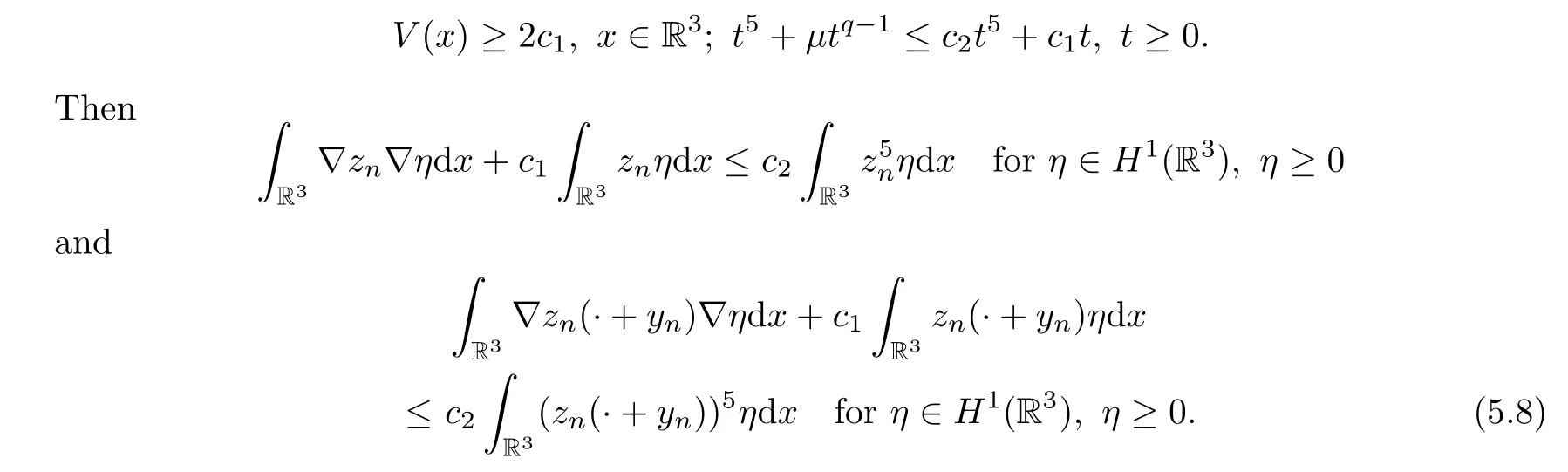
Sincezn(· +yn)=|un(· +yn)|=|wn|?|U|=Zasn→∞inH1(R3),by taking the limitn→∞in (5.8),we obtain that
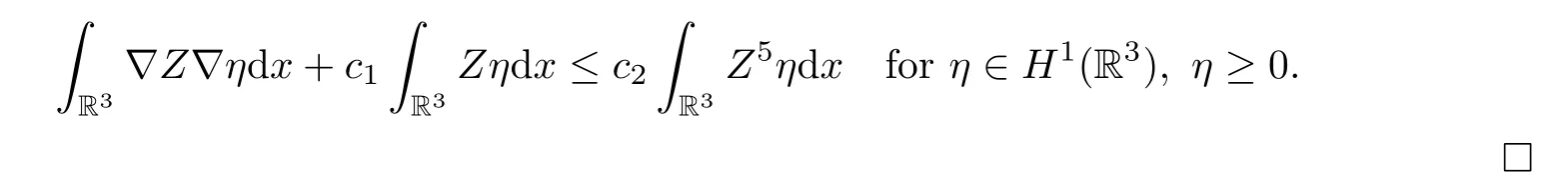
Remark 5.4Assume that the profile decomposition holds.By Lemma 5.3,Zk=|Uk|satisfies the inequality (5.7),and hence there existc,α >0 such that
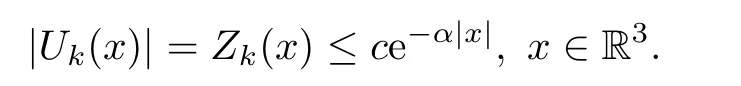
Moreover,takingη=Zkas a test function in (5.7),we have that
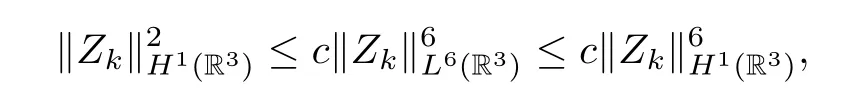
hence there existsm >0 independent ofk∈Λ such that
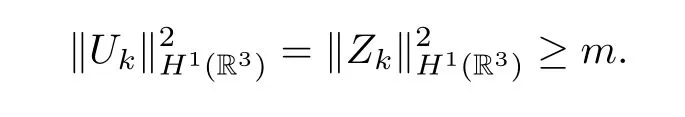
Lemma 5.5The index set Λ of the profile decomposition (5.6) is finite.
ProofIt follows from Remark 5.4 and property (3) of the profile decomposition that Λ is a finite set. □
Denote
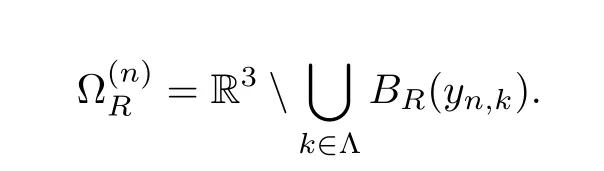
Lemma 5.6There existc,α >0,independent ofn,such that
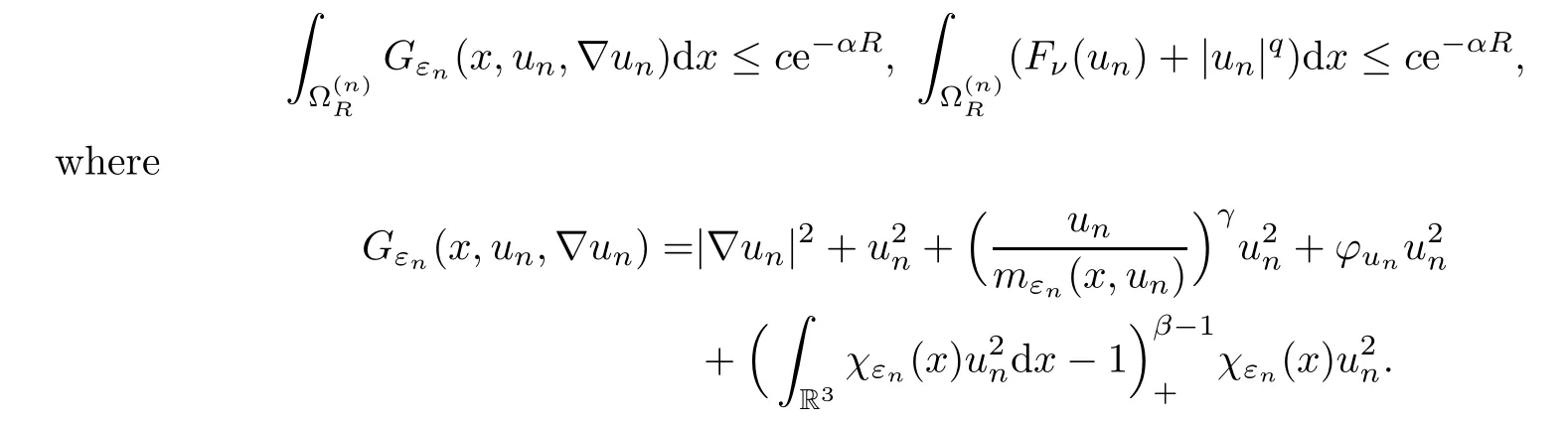
ProofBy Remark 5.4,Ukdecays exponentially.In the profile decomposition ‖rn‖Lp(R3)=o(1),2 ≤p <6.Hence
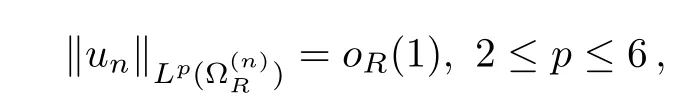
whereoR(1) →0 asR→+∞.By Moser’s iteration (Lemma 5.2,formula (5.5)),

Letφbe aC∞(R3) cut-offfunction such thatφ(x)=0 forand |?φ| ≤2.Choosingη=unφ2as a test function in,we have that
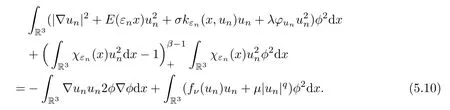
ForRlarge enough,by (5.9),we have that
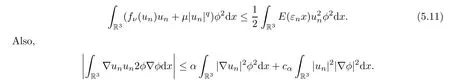
Thus,by (5.10),we have that
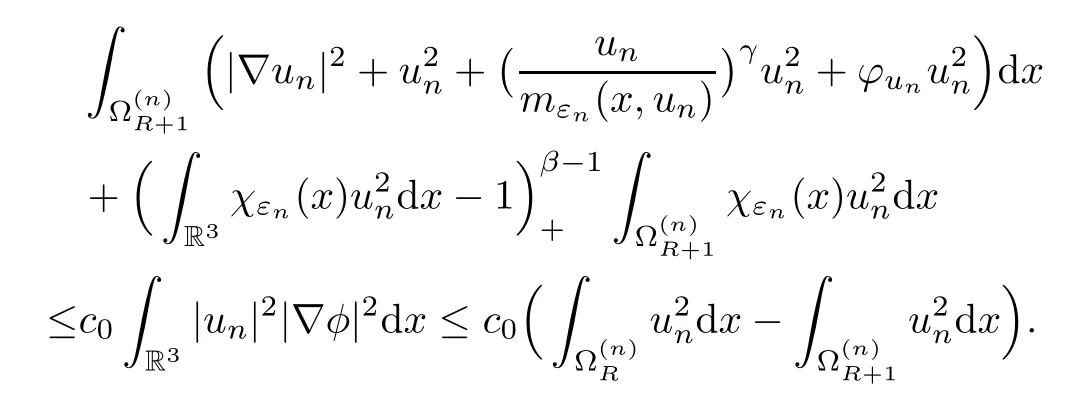

whereα=-lnθ >0.By (5.11),we have that

Without loss of generality,we assume thatδ1<δ2and choose that.Denote that

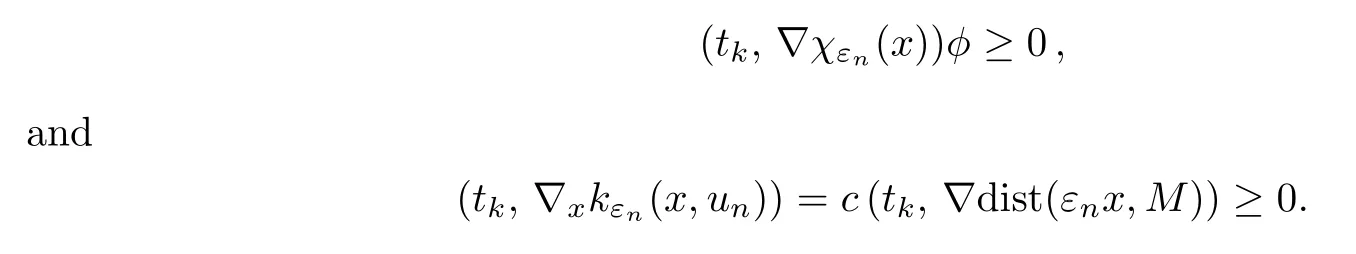
Hence,for the left hand side of (5.14),

For the right hand side of (5.14),

Finally,we estimate the term,since
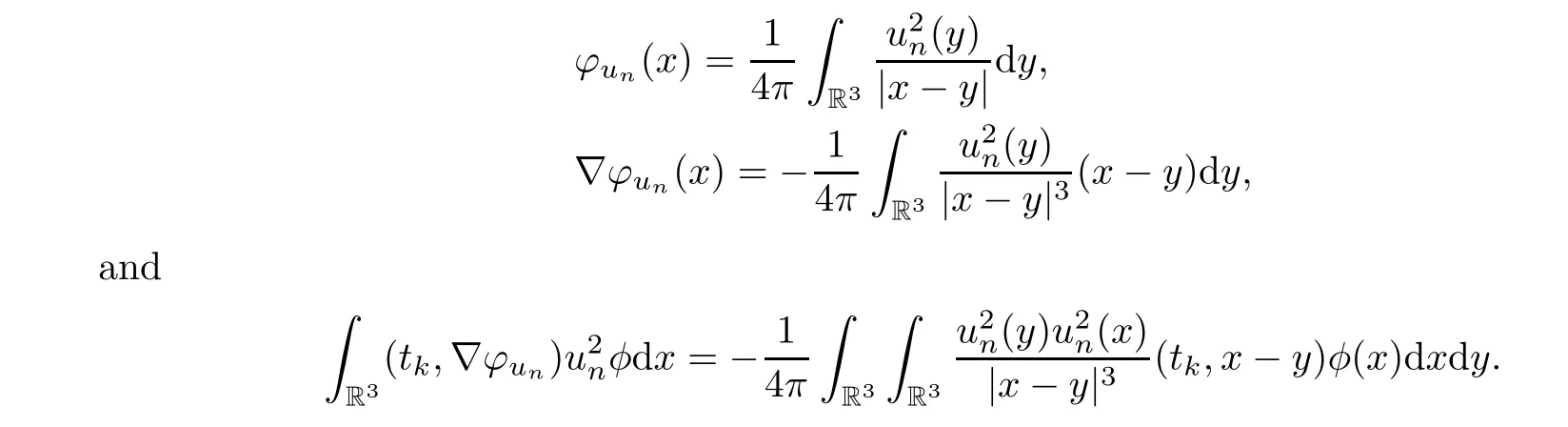
Notice that,by the variable change (x,y)(y,x),we have that
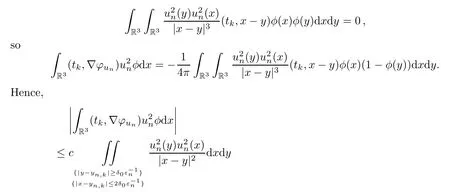

Altogether the left hand side of (5.14) is LHS,and we arrive at a contradiction forεnsufficiently small:□
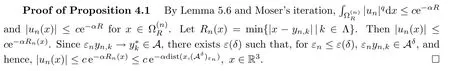
Next we will prove Proposition 4.2.
Lemma 5.8Assume thatu∈H1(R3),L >0,.Thenuis bounded inH1(R3).
ProofSince
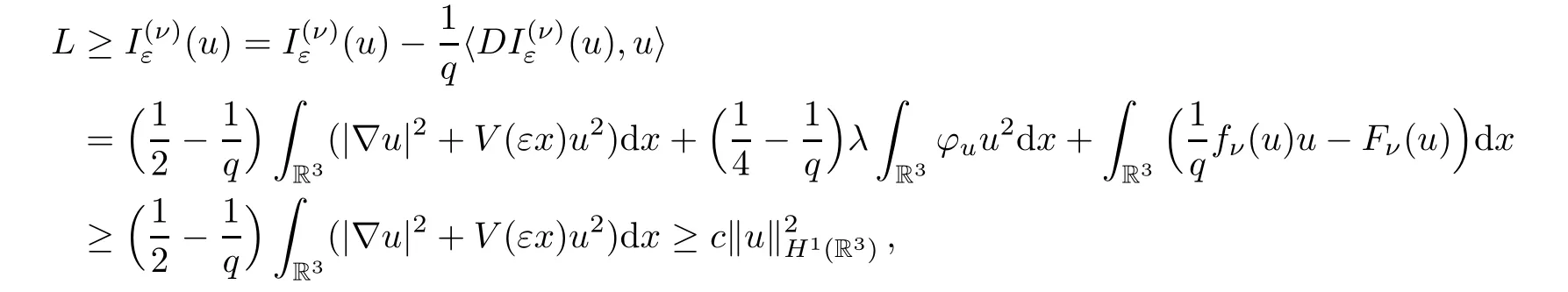
the lemma is proved. □
Assume thatun∈H1(R3),L >0,,νn→0,εn→ε*∈[0,1].The caseνn→ν*∈(0,1] is easier,since we need only to deal with subcritical problems.By Lemma 5.8,unis bounded inH1(R3),we have the following profile decomposition (see [14]):
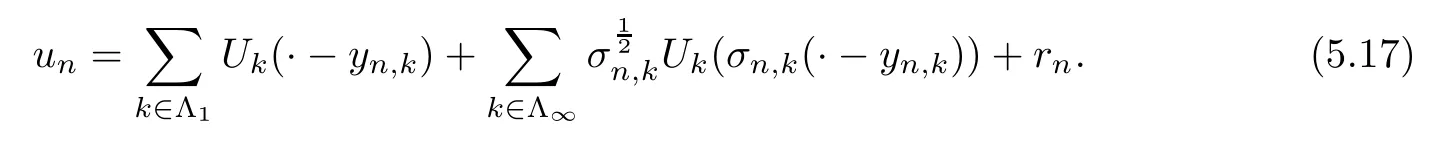
Hereyn,k∈R3,σn,k∈R+andUk∈H1(R3) fork∈Λ1,Uk∈D1,2(R3) fork∈Λ∞,rn∈D1,2(R3),satisfying that
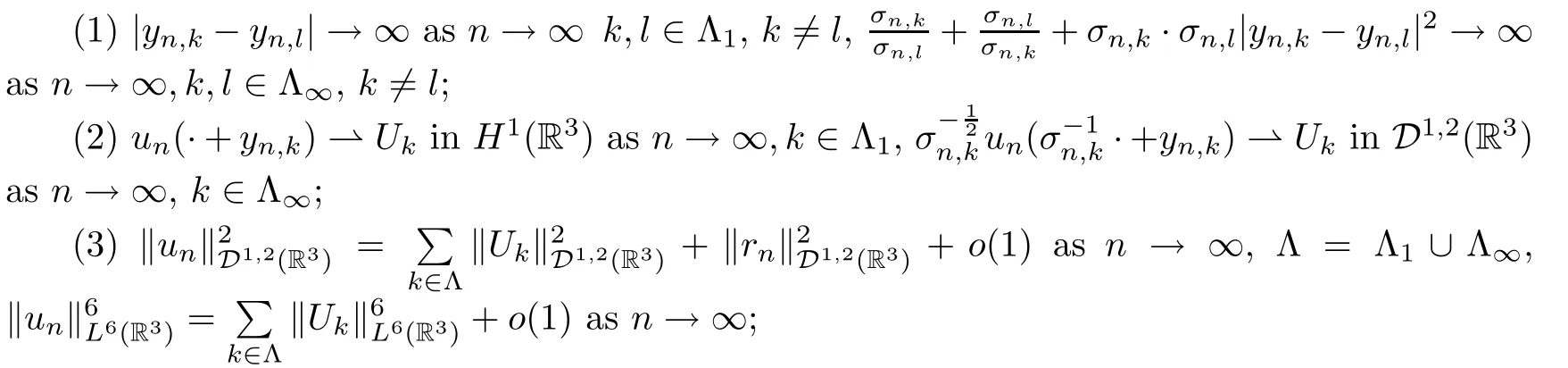
(4)rn→0 inL6(R3) asn→∞.
Lemma 5.9(1) Assume thatyn∈R3,wn=un(· +yn)?UinH1(R3).ThenZ=|U|satisfies that
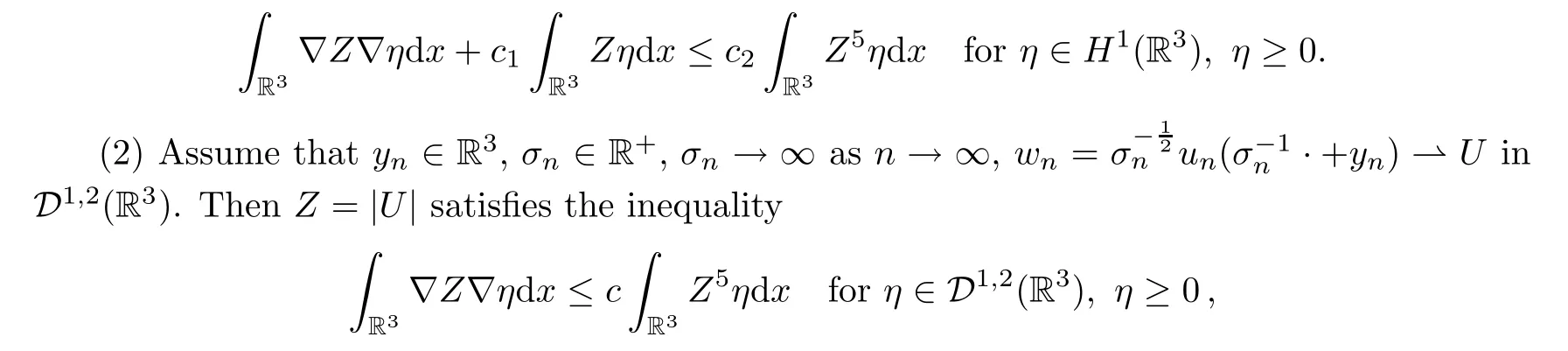
wherec,c1,c2are positive constants.
Proof(1) The proof is the same as Lemma 5.3.(2) Letzn=|un|.As in Lemma 5.3,znsatisfies
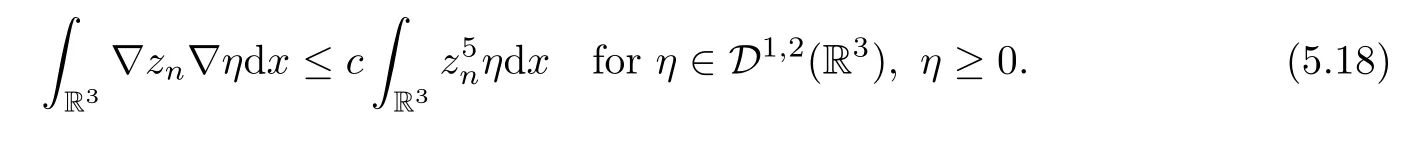
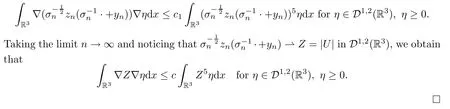
Remark 5.10By Lemma 5.9 there exist positive constantsc,αsuch that
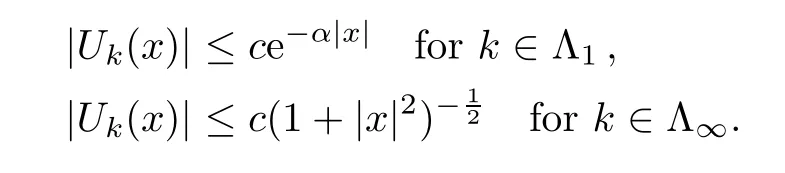
Lemma 5.11The index sets Λ1,Λ∞in the profile decomposition (5.17) are finite.
ProofFork∈Λ1∪Λ∞we have
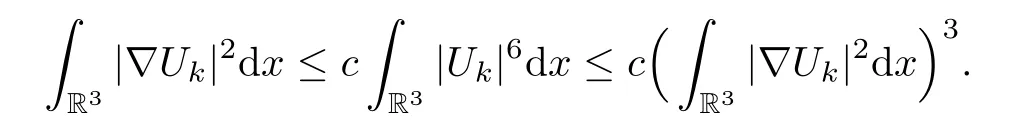
By using the profile decomposition,the following two lemmas can be proved in a similar way as in [5].
Lemma 5.12Assume that the profile decomposition (5.17) holds.Without loss of generality,assume thatσn=σn,1=min{σn,k|k∈Λ∞},yn=yn,1.For 3<p2<6<p1<+∞,it holds that ‖un‖p1,p2,σn≤c,where the norm ‖· ‖p1,p2,σnis defined as
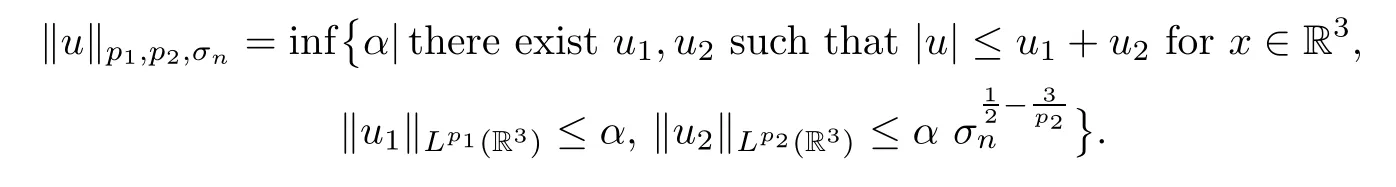
Lemma 5.13There exist positive constantscandcsuch that
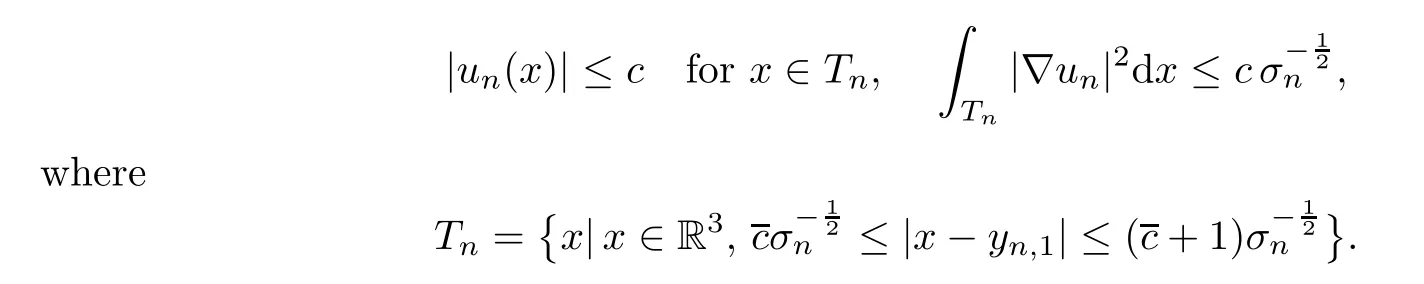
Lemma 5.14The index set Λ∞in the profile decomposition (5.17) is empty.
ProofWe have the local Pohoˇzaev identity
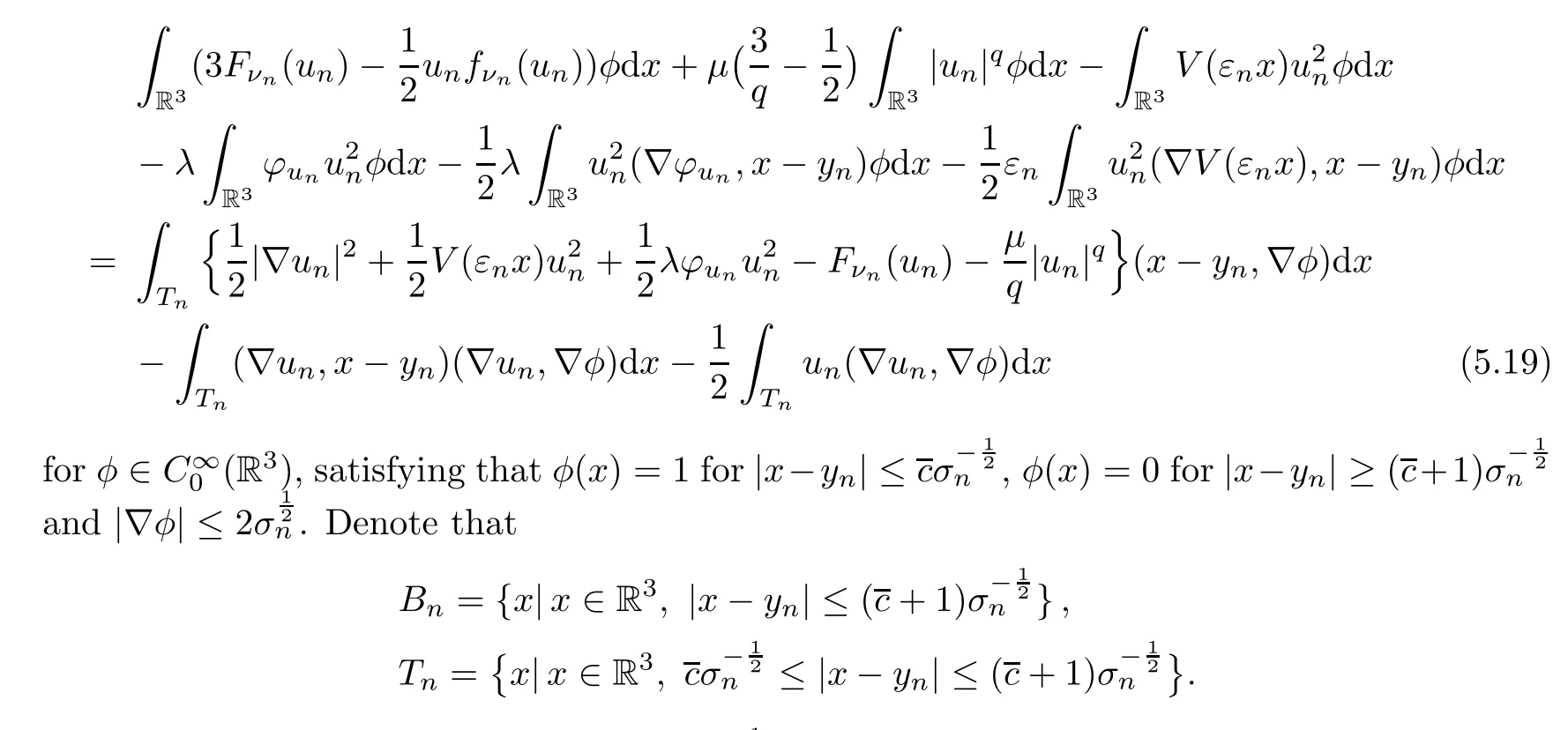
Notice that in the regionTn,andφun(x) ≤cforx∈R3.By Lemma 5.13,the right hand side of (5.19) is
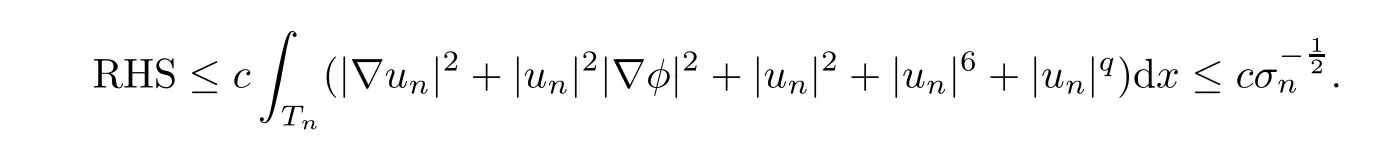
For the terms on the left hand side of (5.19),we have
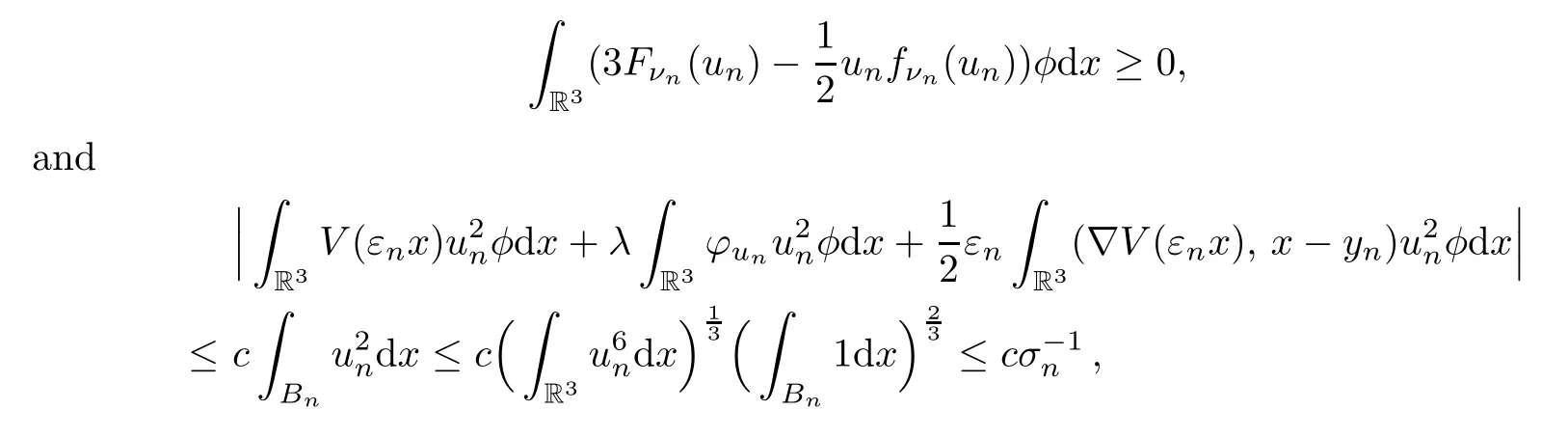

We arrive at a contradiction forσnlarge enough andq >5:

Proof of Proposition 4.2By Lemma 5.14 and the profile decomposition,(5.17) reduces to
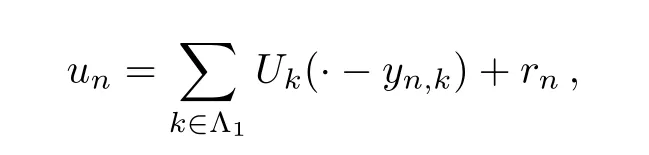
wherern→0 inL6(R3) asn→∞andUk,k∈Λ1satisfies the estimate |Uk(x)| ≤ce-α|x|for somec,α >0.Now,by theε-regularization theorem for the elliptic equation with critical growth and Moser’s iteration,we conclude thatunare uniformly bounded,that is,there exists a constantMdepending onL,but not onn,such that

Appendix
We also consider the subcritical case with a general nonlinearity,namely,
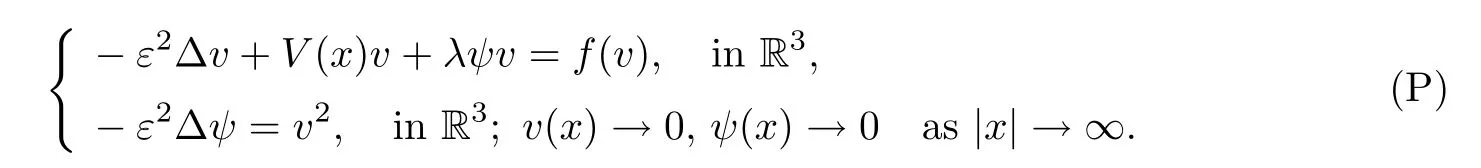
For the nonlinear functionf,we assume that
(F)fis a continuous function satisfying that
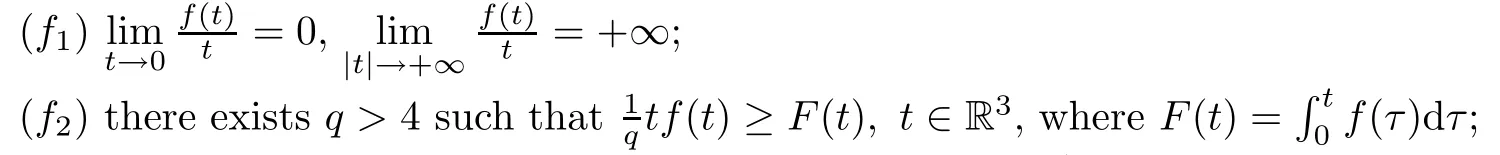
(f3) there existc >0,r <6 such that |f(t)| ≤c(1 +|t|r-1).
Obviously,the functionf(t)=|t|q-2t,q∈(4,6) satisfies the assumption (F).
Theorem A.1Assume (V) and (F).Then,for any positive integerk,there existsεk>0 such that,if 0<ε <εk,the problem (P) has at leastkpairs of nodal solutions ±vj,ε,j=1,2,···,k.Moreover,for anyδ >0,there existα >0,c=ck>0 andεk(δ)>0 such that,if 0<ε <εk(δ),then it holds that
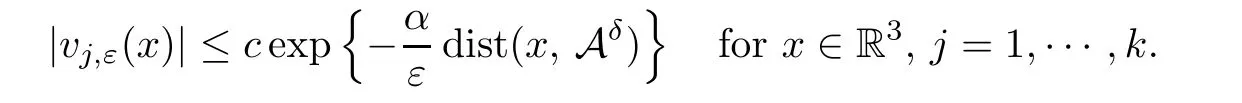
 Acta Mathematica Scientia(English Series)2022年5期
Acta Mathematica Scientia(English Series)2022年5期
- Acta Mathematica Scientia(English Series)的其它文章
- ERRATUM TO: SEEMINGLY INJECTIVE VON NEUMANN ALGEBRAS(Acta Mathematica Scientia,2021,41B(6): 2055–2085.)*
- EXPONENTIAL STABILITY OF A MULTI-PARTICLE SYSTEM WITH LOCAL INTERACTION AND DISTRIBUTED DELAY*
- THE ASYMPTOTIC BEHAVIOR AND SYMMETRY OF POSITIVE SOLUTIONS TO p-LAPLACIAN EQUATIONS IN A HALF-SPACE*
- GLOBAL WELL-POSEDNESS FOR THE FULL COMPRESSIBLE NAVIER-STOKES EQUATIONS*
- POINTWISE SPACE-TIME BEHAVIOR OF A COMPRESSIBLE NAVIER-STOKES-KORTEWEG SYSTEM IN DIMENSION THREE*
- PROBING A STOCHASTIC EPIDEMIC HEPATITIS C VIRUS MODEL WITH A CHRONICALLY INFECTED TREATED POPULATION*
