FAN Mingzhi(樊明智)

( School of Science,Xuchang University,Xuchang 461000, China)

Abstract:A low order H1-Galerkin mixed finite element method (for short FEM) is proposed for a class of nonlinear dispersion dissipative wave equations with the simplest bilinear rectangular element and zero order Raviart-Thomas(for short R-T) element.By use of the interpolation operator instead of the traditional Ritz projection,together with integral identity technique,the superclose properties of u in H1-norm and →p in H(div,Ω)-norm are deduced for the semi-discrete and fully-discrete schemes,which improve the results in the associated existing literature.Finally,numerical results are provided to confirm the validity of our theoretical analysis.

Key words:Nonlinear dispersion dissipative wave equations; H1-Galerkin MFEM;Superclose property;Semi-discrete and fully-discrete schemes

1.Introduction

Consider the following dispersion-dissipative wave equations[1]

whereΩis a convex polygonal domain in R2with bounded boundary?Ω,J=(0,T] is the time interval,X=(x,y),u0(X),u1(X) are known smooth functions,f(u) is a Lipschitz continuous function.

The nonlinear dispersion-dissipative wave equations (1.1) are usually used to diserible the propagation problems of lenghways-wave in nonlinear elastic rods and ion-sonic of space transformation by weak nonlinear effect,and there have been appeared some studies.For example,[1] discussed this problem which initial boundary value condition;[2-4] studied solitary wave solution,[5-6] proved existence and asymptotic behaviour of the global solution,respectively;[7] investigated mixed covolume methods;[8] derived convergence results for semi-discrete and the backward Euler fully-discrete schemes;although,[9] deduced the superclose properties and the superconvergence results of conforming linear triangular FEM,however.Unfortunately,there is no consideration on Crank-Nicolson fully-discrete scheme of equations (1.1),up to now.

In recent years,a lot of studies have been devoted to mixed FEMs for partial differential eauation[10-21].For example,[10-11] established the general theory of Mixed FEMs;[12]developed a new FEM called expand Mixed FEMs.However,the pair of the approximating spaces has to satisfy the LBB consistency condition on the approximating spaces.[13]proposed theH1-Galerkin Mixed FEMs,and has been applied to different PDEs.For exemple parabolic partial integro-differential equations[14],second order hyperbolic equations[15],hyperbolic type integro-differential equation[16],Sobolev equations[17]and pseudo-hyperbolic equations[18],etc.

At present work,we mainly study the superclose properties of the lowest orderH1-Galerkin mixed FEM for equations (1.1) under semi-discrete and fully-discrete schemes.the bilinear FE and the zero order R-T FE spaces are taken as approximation spaceV hfor the original variableuandfor the stress=?ut,respectively.Firstly,we derive the superclosed properties with orderO(h2) foruinH1-norm and forinH(div,Ω) for semidiscrete scheme.Secondly,we obtain the superclosed results with orderO(h2+Δt)/O(h2+(Δt)2) foruinH1-norm and for→pinH(div,Ω) under backward Euler and Crank-Nicolson fully-discrete schemes,respectively.The results of this paper for semi-discrete scheme and Euler fully-discrete scheme is one order higher than the results with respect tohin[18].This proposed mixed FE scheme has a smallest total degrees of freedom (about 3NP,NP denotees the numbers of the nodal points in the subdivision).

Throughout this paper,hand Δtdenote the mesh size and the time step,respectively.Cdenotes a general positive constant which does not depend onhand Δt,andCmay represent different values in different places.

2.Construction of Mixed FEs and Two Important Lemmas

3.Superclose Analysis for Semi-discrete Scheme

We reurite the problem (1.1) into the following system

4.Superclose Analysis of the Backward Euler Fully-discrete Scheme

In this section,we will derive the error estimates between the exact solution an its approximation solution for fully-discrete scheme.

Let 0=t0＜t1＜...＜tN-1＜tN=Tbe a given partition of the time interval [0,T]with step length Δt=T/N,tn=nΔt,n=1,2,···,N,for some positive integerN.Next,we introduce some notations as follows

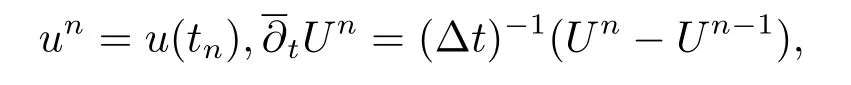
5.Superclose Analysis of the Crank-Nicolson Fully-discrete Scheme

6.Numerical Results

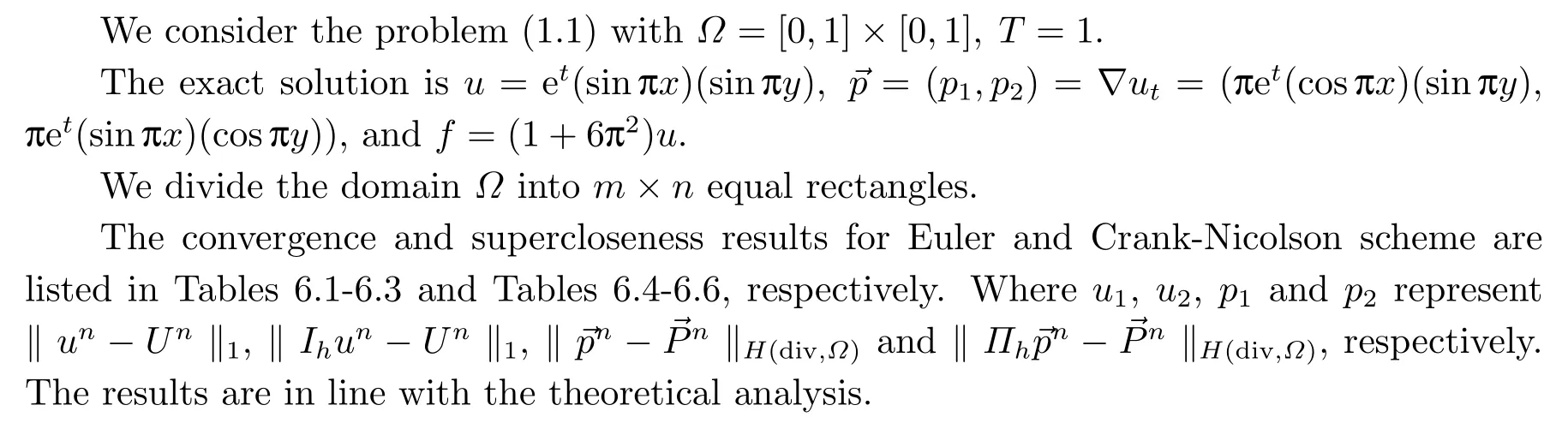
Tab.6.1 Numerical results for Euler scheme at t=0.1

Tab.6.2 Numerical results for Euler scheme at t=0.5

Tab.6.3 Numerical results for Euler scheme at t=1.0

Tab.6.4 Numerical results for Crank-Nicolson scheme at t=0.1

Tab.6.5 Numerical results for Crank-Nicolson scheme at t=0.5

Tab.6.6 Numerical results for Crank-Nicolson scheme at t=1.0