關于非齊次樹指標m重馬氏信源的一個強極限定理
2022-10-31 12:39:38金少華田雪然
應用數(shù)學 2022年4期
金少華,田雪然
(河北工業(yè)大學理學院,天津 300401)
1.引言
樹指標隨機過程已成為近年來發(fā)展起來的概率論的研究方向之一.強極限定理一直是國際概率論界研究的重要課題.楊等人在文[1]中給出了關于樹指標非齊次馬氏鏈的廣義熵遍歷定理.ZHONG等在文[2]中通過引入樹指標馬爾科夫鏈的概念,證明了Cayley樹指標下馬爾科夫鏈關于二元函數(shù)延遲和的一個強極限定理.ZHONG等在文[3]中首先引入漸近對數(shù)似然比作為二叉樹上任意隨機場與分叉馬爾科夫鏈之間偏差的度量,然后通過構造一個非負鞅,建立了二叉樹指標馬爾科夫鏈的一類強偏差定理.WANG等在文[4]中給出了連續(xù)狀態(tài)非齊次馬氏鏈滑動平均的強大數(shù)定律.李世林等人在文[5]中研究了在有限狀態(tài)空間取值的二叉樹上非齊次馬氏鏈轉移概率調(diào)和平均的極限性值.金少華等人在文[6]中給出了非齊次樹上馬氏雙鏈轉移矩陣的一個強極限定理.本文通過引入相對熵密度偏差的概念和構造非負鞅,研究給出了關于非齊次樹指標m重馬氏信源的一個強極限定理.
2.基本概念
設T是一個具有根頂點o的無限樹,{Nn,n ≥1}是一列正整數(shù)集,如果T的第n(n ≥0)層上的每個頂點均與第n+1層上的Nn+1個頂點相鄰,則稱T為廣義Bethe樹或廣義Cayley樹.特別地,若對非負整數(shù)集N,用模m的同余關系對其分類得到如下模m的剩余類
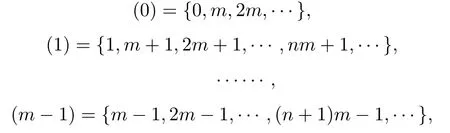

3.強極限定理




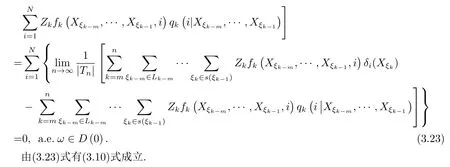
猜你喜歡
大江南北(2023年2期)2023-02-11 05:45:56
電腦報(2022年37期)2022-09-28 05:31:07
數(shù)學物理學報(2021年3期)2021-07-19 06:02:44
現(xiàn)代計算機(2021年14期)2021-07-09 17:19:40
數(shù)學物理學報(2020年6期)2021-01-14 01:00:44
數(shù)學年刊A輯(中文版)(2020年1期)2020-05-19 00:30:50
數(shù)學物理學報(2018年2期)2018-05-14 07:32:07
雜文月刊(2017年18期)2017-11-12 17:35:00
武漢輕工大學學報(2016年4期)2017-01-16 08:53:03
領導文萃(2016年6期)2016-12-26 10:13:55
- 應用數(shù)學的其它文章
- A Sufficient Condition for the Noncorrelation of Binary Pattern Sequences
- The Effects of θ on Stability in the θ-Milstein Method for Stochastic Differential Equations
- 基于分布式大數(shù)據(jù)的Expectile回歸分析
- 具有時滯的Lotka-Volterra食餌-捕食者成年種群模型的穩(wěn)定性分析
- 求解多目標優(yōu)化問題的非單調(diào)牛頓法的超線性收斂性
- 固定效應變系數(shù)空間自回歸面板數(shù)據(jù)模型的空間效應檢驗

