時(shí)統(tǒng)業(yè),曾志紅

(1. 海軍指揮學(xué)院,江蘇 南京 211800; 2. 廣東第二師范學(xué)院 學(xué)報(bào)編輯部,廣東 廣州 510303)

1 相關(guān)知識(shí)

定理1[1](Ostrowski 不等式)設(shè) :f[a,b]→R 在[a,b]上連續(xù),在(a,b)上可微,則對任意 x ∈[a,b],有

文[2]證明了若f 在[a,b]上滿足M-Lipschitz 條件,即對任意 t1,t2∈[a,b],有 | f(t2)-f(t1)|≤M |t2- t1|,則Ostrowski 不等式也成立．

利用Grüss 不等式[3],可建立Ostrowski-Grüss 型不等式. 關(guān)于Ostrowski 型不等式和Ostrowski-Grüss型不等式的結(jié)果見文[4～11]．本文參照文[12]引入?yún)?shù)求最值的方法,建立若干帶有參數(shù)的不等式,在特殊情況下得到Ostrowski 型不等式和Ostrowski-Grüss 型不等式的加強(qiáng)．

為方便起見,引入記號

引理1[4]設(shè)f 在[a,b]上可微,且f＇在[a,b]上可積,λ∈ [0,2],則對于任意 x ∈[a,b],有

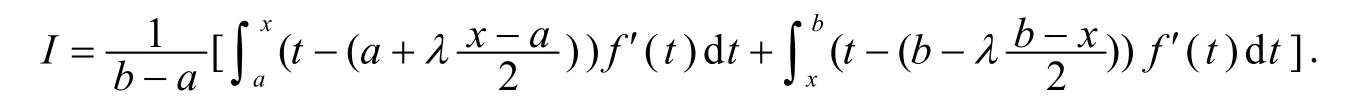
引理2設(shè)f在[a,b]上二階可微,且f＇在[a,b]上可積,λ∈[0,2],則對于任意x∈[a,b],有

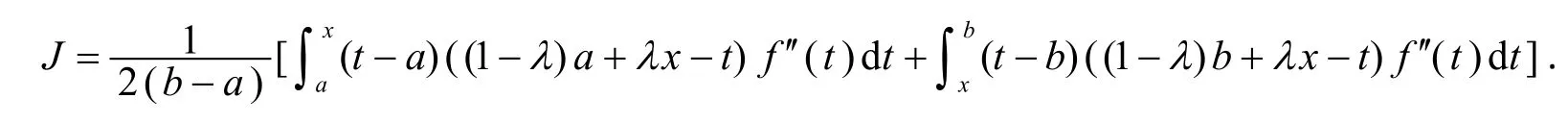
2 主要結(jié)果

定理2設(shè)f在[a,b]上可微,且f＇在[a,b]上可積,存在常數(shù)γ和Γ(γ＜Γ),使得對于任意t∈[a,b],有γ≤f＇(t)≤Γ,則對于任意λ∈[0,2]和任意x∈[a,b],有

其中

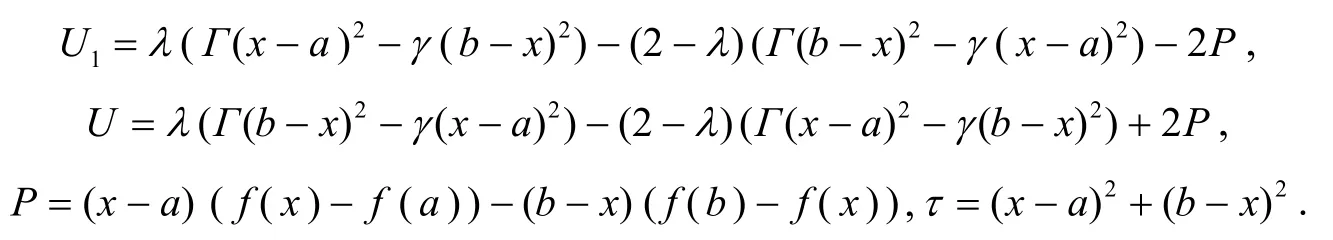
證明先考慮x≠a的情形．將P表示為

利用式(2)得γ(x-a)2-Γ(b-x)2≤P≤Γ(x-a)2-γ(b-x)2,于是有 -(2 -λ)τ(Γ-γ)≤U≤λτ(Γ-γ),從而在式(3)中取ε=ε1,則式(1)的右邊不等式得證.

再考慮x=a的情形．記對任意常數(shù),由引理1 得

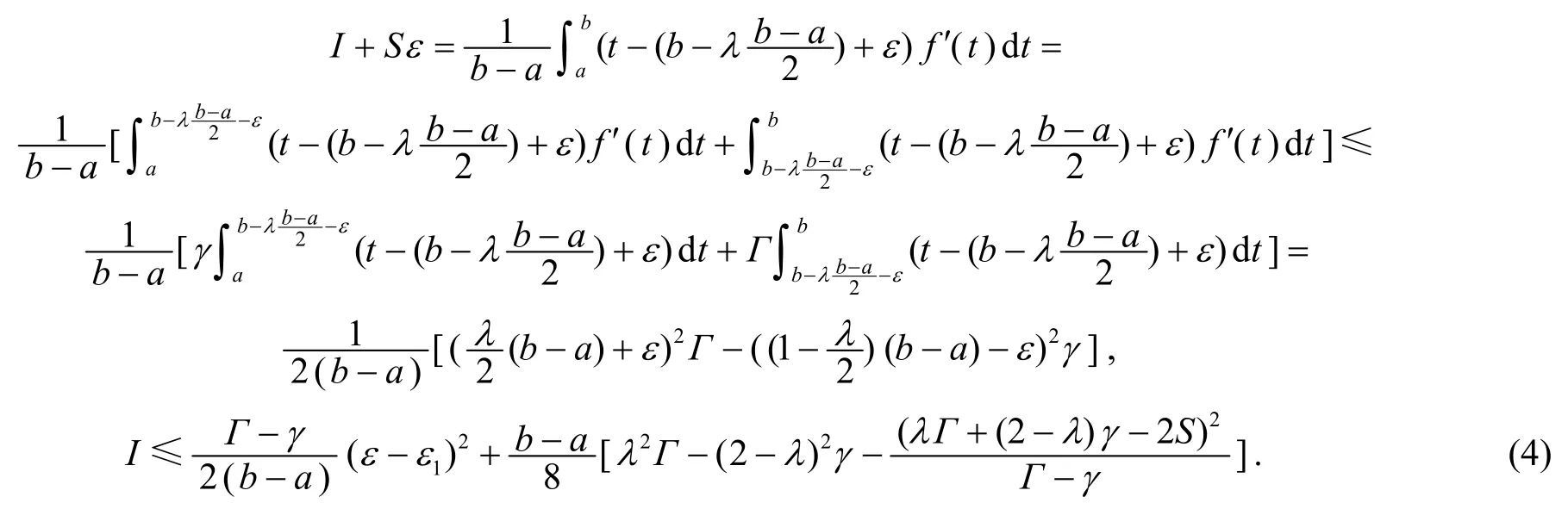
推論1設(shè)條件同定理2,則對任意λ∈ [0,2]和任意x∈[a,b],有

證明如果A1+B1≤I≤A2-B2,則A1+min{B1,B2} ≤I≤A2-min{B1,B2},從 而利用這個(gè)事實(shí),由定理2 即得推論.

注1推論1 是文[5]定理的加強(qiáng)．

推論2設(shè)f在[a,b]上可微,f＇在[a,b]上可積,存在常數(shù)γ和Γ(γ＜Γ),使得對于任意t∈[a,b],有γ≤f＇(t)≤Γ,則對任意λ∈ [0,2],有

證明在定理2 中取x=a即可得證．

注2因?yàn)?/p>

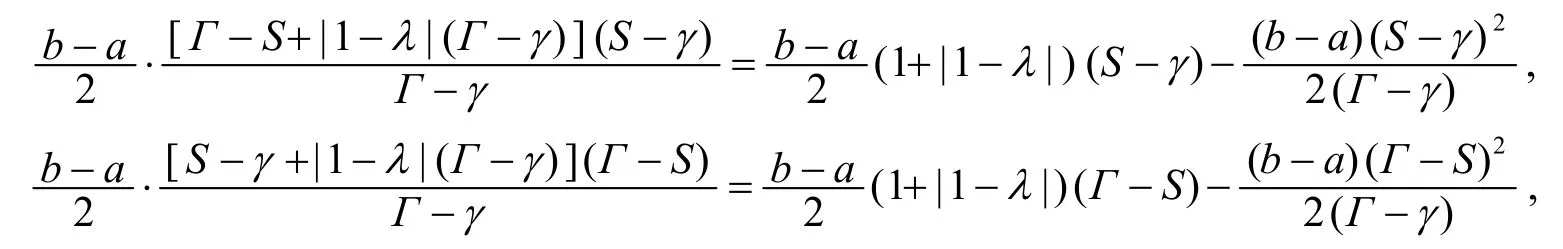
所以推論2 為文[4]推論5 中不等式的加強(qiáng)．

推論3設(shè)f在[a,b]上可微,f＇在[a,b]上可積,存在常數(shù)γ和Γ(γ＜Γ),使得對于任意t∈[a,b],有γ≤f＇(t)≤Γ,則對任意λ∈ [0,2],有

證明在定理2 中取即可得證.

推論4設(shè)條件同定理2,則對任意x∈[a,b],有

證明在定理2 中取λ= 0即可得證．

推論5設(shè)f在[a,b]上可微,f＇在[a,b]上可積,存在常數(shù)M,使得對于任意t∈[a,b],有|f＇(t)|≤M,則對任意x∈[a,b],有

證明在推論4 中取Γ=-γ=M即可得證．

注3推論5 給出了Ostrowski 不等式的加強(qiáng)．

推論6設(shè)條件同定理2,則對任意x∈[a,b],有

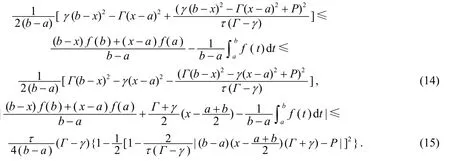
證明在定理2 中取λ= 2即可得證．

定理3設(shè)f:[a,b]→R 滿足(γ,Γ)-Lipschitz 條件,即存在常數(shù)γ和Γ,使得對于任意s,t∈[a,b],s＜t,有γ(t-s)≤f(t)-f(s)≤Γ(t-s),則對任意λ∈ [0,2],x∈[a,b],式(1)成立．

證明當(dāng)x≠a時(shí),對任意常數(shù)有

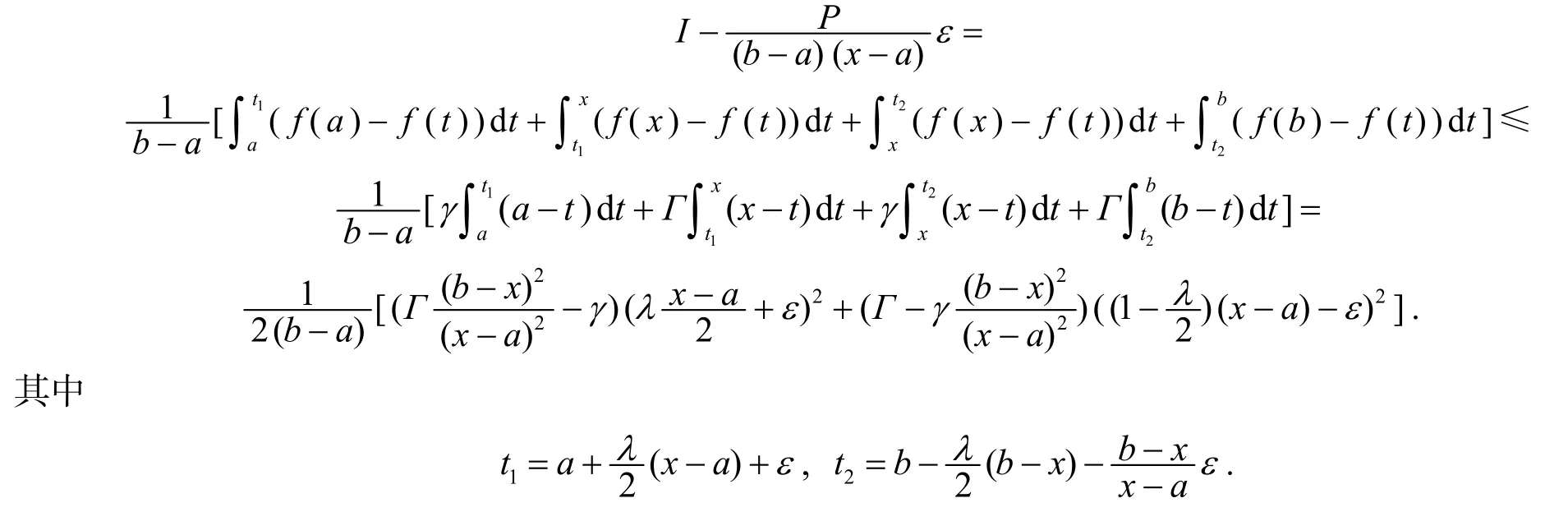
當(dāng)x=a時(shí),對任意常數(shù)有

以下證明同定理2,故略去．

推論7設(shè)條件同定理3,則對任意λ∈[0,2]和任意x∈[a,b],式(5)成立; 對任意λ∈ [0,2],式(11)～(15)成立．

推論 8設(shè)條件同定理3,則對任意λ∈ [0,2],式(6)～(10)成立．

定理4設(shè)f在[a,b]上二階可微,f＇在[a,b]上可積,存在常數(shù)γ和Γ(γ＜Γ),使得對于任意t∈[a,b],有γ≤f＇≤Γ,則對于任意λ∈ [0,2]和任意x∈[a,b],有

證明先考慮x≠a的情形．對任意常數(shù)ε∈ [-λ(x-a),(1 -λ)(x-a)],由引理2 得

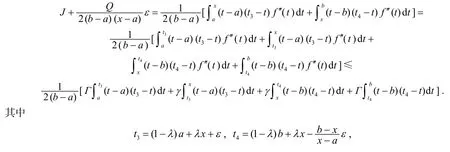
在式(17)中取ε=ε3,則式(16)的右邊不等式得證．

再考慮x=a的情形．對于任意常數(shù)ε∈ [-λ(b-a),(1 -λ)(b-a)],令t5=(1 -λ)b+γa-ε,則

在式(18)中取ε=ε4則式(16)的右邊不等式也成立. 當(dāng)γ≤f＇(t)≤Γ時(shí),-Γ≤ -f＇(t)≤ -γ,對-f應(yīng)用已證明的結(jié)果,則式(16)的左邊不等式得證．

推論9設(shè)條件同定理4,則對任意x∈[a,b],有

進(jìn)而有

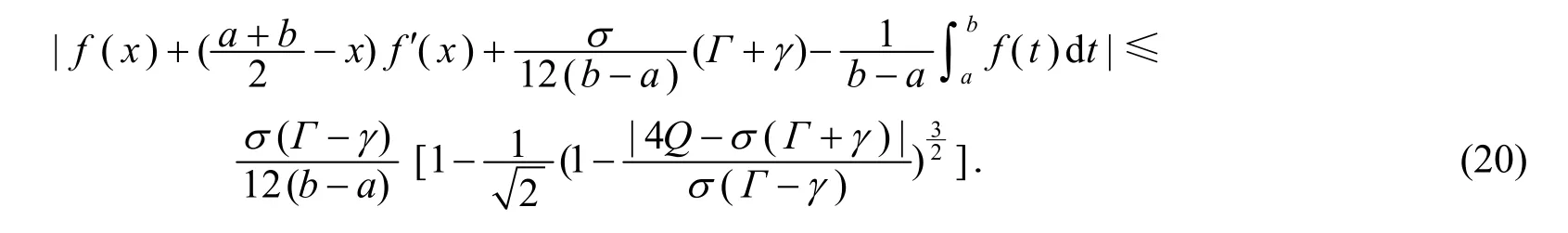
證明在定理4 中取λ= 0即可得證．

推論10設(shè)條件同定理4,則對任意x∈[a,b],有

進(jìn)而有

其中

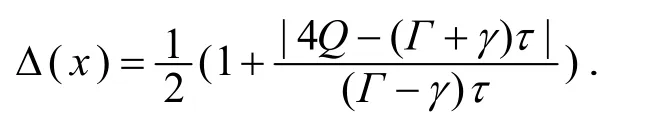
證明在定理4 中取λ=1 即可得證．

注4注意到,所以式(21)是文[10]式(8.5)的推廣和加強(qiáng)．

定理5設(shè)f:[a,b]→R 滿足(γ,Γ)-Lipschitz 條件,即存在常數(shù)γ和Γ,使得對于任意s,t∈ [a,b],s＜t,有γ(t-s)≤f＇(t)-f＇(s)≤Γ(t-s),則對任意λ∈[0,2],x∈[a,b],式(16)成立．

證明先考慮x≠a的情形．對任意常數(shù)ε∈ [-λ(x-a),(1 -λ)(x-a)],有

再考慮x=a的情形．對于任意常數(shù)ε∈ [-λ(b-a),(1 -λ)(b-a)],令t5=(1 -λ)b+γa-ε,則

接下來的證明類似于定理4,故略去過程．

推論11設(shè)條件同定理5,則對任意x∈[a,b],式(19)和式(20)成立．

推論12設(shè)條件同定理5,則對任意x∈[a,b],式(21)和式(22)成立．