Guan Wang(王冠), Zhixia Ding(丁芝俠), Sai Li(李賽), Le Yang(楊樂(lè)), and Rui Jiao(焦睿)

Hubei Key Laboratory of Optical Information and Pattern Recognition,School of Electrical and Information Engineering,Wuhan Institute of Technology,Wuhan 430205,China

Keywords: finite-time Mittag–Leffler synchronization, fractional-order complex-valued memristive neural networks,time delay

1. Introduction

As a crucial component of artificial intelligence, neural networks have been widely applied in optimization, signal processing,associative memory,parallel computation,pattern recognition, artificial intelligence, image processing, control system,and so on.[1–5]Most of the related results concentrate on real-valued neural networks(RVNNs).[6–8]Notably,the research direction of neural networks is changing from the traditional real-valued domain to the complex-valued domain,and some scholars are beginning to study complex-valued neural networks(CVNNs).[9]Compared with RVNNs,CVNNs have more complex characteristics and wider practical applications,which make it possible to solve those problems that RVNNs cannot, for instance, the problem of XOR[10]and the detection problem of symmetry.[11]Nowadays,an increasing number of scholars carry out the study on CVNNs,[12–15]and the potential of CVNNs in electromagnetic, optoelectronics, filtering, remote sensing, signal processing, and other areas are also developed.[16–20]

Fractional-order calculus can describe the systems with genetic and memory properties more accurately due to its nonlocality and infinite memory.[21–25]In recent years,fractionalorder complex-valued neural networks(FCVNNs)have drawn extensive attention and some interesting phenomenons have been reported.[26–34]It is noteworthy that most of the research methods are based on splitting the FCVNNs into two real-valued systems and obtaining the relevant conditions by studying these real-valued systems. Since the separation of complex-valued activation functions cannot always be explicitly separated and the increase in system dimensionality may lead to the complexity of system analysis. Therefore, it may be more valuable to analyze the FCVNNs as an entirety. In Ref. [34] we considered the FCVNNs as an entirety and obtained the global dissipativity and quasi-Mittag–Leffler synchronization of the systems by proposing a new fractionalorder inequality.

In 1971, Chua first introduced the nonlinear resistive element which is called the memristor.[35]Since memristors have memory properties similar to biological synapses,the memristive neural networks (MNNs) can better simulate the human brain and have been widely used in novel biological models for associative memory, real-time encoding and compression, optimization with massively parallel computing,[36–39]etc. Nowadays, some interesting results on fractional-order complex-valued memristive neural networks(FCVMNNs)have been published.[40–45]However,due to the limited switching speed of the amplifier,time delay is unavoidable in neural network circuits,which could influence the stability of the system.[45,46]Taking these facts into consideration,time delay should be considered in the FCVMNNs.

Synchronization was raised by Pecora and Carroll in 1990,[47]which denotes the phenomenon of system states consistency in time. In recent years, synchronization has been widely applied in secure communication, information processing, biology,[48–50]etc. Currently, related synchronization results of FCVMNNs have been studied in literature.[41,43,44,51,52]In Ref.[41],by designing a simple linear feedback controller, the global asymptotical synchronization of FCVMNNs with parameter uncertainties and multiple time delays was derived according to the comparison principle. By using the Gronwall–Bellman integral inequalities and feedback control technique,the finite-time projective synchronization of FCVMNNs with time delays was achieved in Ref. [43]. The ultimate Mittag–Beffler synchronization of FCVMNNs with time delays was achieved by the fractionalorder Leibniz rule, Razumikhin-type method and complexvalued adaptive controller in Ref. [44]. In Ref. [51], the authors dealt with the complex projection synchronization for a class of FCVMNNs with multiple delays by employing the hybrid control strategy. Some sufficient criteria were obtained to ensure the quasi-synchronization of FCVMNNs with switching jumps mismatch by constructing a suitable Lyapunov function in Ref.[52]. Note that most scholars concentrate on asymptotic behavior, which means that synchronization is achieved when the time is infinite. Compared to the infinite-time synchronization, the finite-time synchronization has a faster convergence speed and better robustness,[53]which is more reasonable in realistic applications. It is worth noting that finite-time synchronization has been applied in many practical applications, such as image encryption and satellite positioning. Hence,it is indispensable to investigate the finitetime synchronization of FCVMNNs.

Taking into account the above factors,in this paper we investigate the FTMLS of FCVMNNs with time delay, and the major contributions are summarized as follows:

(i) Unlike the traditional separation technique in Refs. [26,28,29,32,40–45], this paper considers the FCVMNNs as an entirety. Based on the property of complexvariable function and Lyapunov stability theorem, some sufficient conditions are established to realize the FTMLS of FCVMNNs with time delay.

(ii) Based on the complex-valued sign function, a novel complex-valued feedback controller is devised to realize the FTMLS of FCVMNNs with time delay. By adjusting controller parameters, the FTMLS of FCVMNNs with and without time delay can also be realized. In addition, the asymptotic synchronization of FCVMNNs with time delay can be obtained by utilizing the comparison theorem, which extends the existing results in Refs.[33,42,43].

(iii) The upper bound of synchronization settling time(SST) can be estimated by establishing a new fractional differential inequality. Moreover, compared with the previous results in Ref. [43], the upper bound of SST in this paper is more flexible and less conservative.

This article proceeds as follows. In Section 2,some preliminaries are given. The main results and simulation examples are provided in Sections 3 and 4,respectively. Finally,the summary is provided in Section 5.

2. Preliminaries and system description

2.1. Preliminaries

Definition 1[54]g(t):[0,+∞)→C is an integrable function and the fractional-order integral ofg(t)is

Ifσ ＞0 andιi ＞0,then limt→+∞L(t)=0.

2.2. System description

whereε ∈(0,1);si(t)∈Cnrepresents the state of thei-th neuron at the timet;ci ＞0 denotes the self-regulating constant;fj(·),gj(·)∈C are the activation functions of thej-th neuron at the timetandt-τ, respectively;Ii(t)∈C denotes the external input;si(0)=si0∈C is the initial condition of Eq.(2);ai j(sj(t))andbi j(sj(t))are complex-valued memristive weights,defined by

In FCVMNNs (2) and (3), the memristive connection weightsai j(·)andbij(·)are discontinuous.Thus,we deal with such systems under the framework of Filippov solution.[56]

Through the differential inclusion theory,system(2)can be transformed to

fori,j ∈N+,or there existφij(t)∈K[aij(sj(t))]andβij(t)∈K[bij(sj(t))]such that

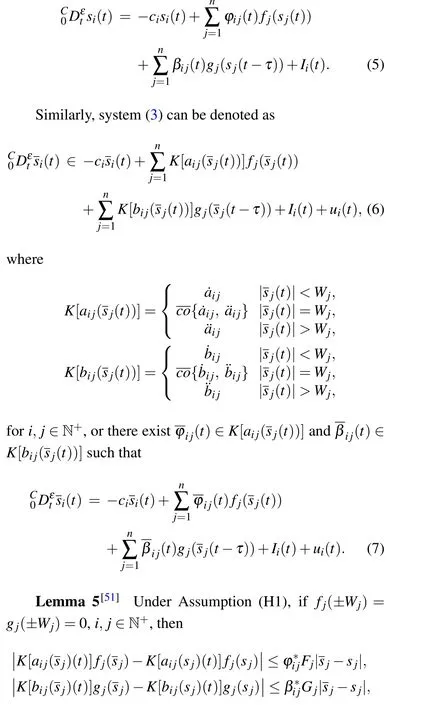
is called the upper bound of SST. Particularly, whenε=1,the FTMLS are reduced to the finite-time exponential synchronization.

3. Main results

which shows that the error system (10) is Mittag–Leffler stable. In other words, it means that the systems(2)and(3)are Mittag–Leffler synchronization.

In the following,the SST of systems(2)and(3)is given.

From Eq.(17),we have w w

Therefore,the state trajectories of systems(2)and(3)can be synchronized withinT1under controller(9).

Remark 1 From Theorem 1,we can realize that the SSTT1decreases monotonically with respect to the controller gainξi. This means that the SSTT1can be adjusted by flexibly changing the controller parameters,which improves the reliability and safety of systems.

Remark 4 The proof of Corollary 2 is similar to Theorem 1. In Theorem 3 of Ref.[33],the finite-time synchronization of FCVNNs was investigated by the property of complexvariable functions. However,time delay and memristive connection weights are not discussed in Ref. [33]. Hence, the result of Corollary 2 can be seen as the generalization of Theorem 3 in Ref.[33].

When neglecting the effect of|zi(t-τ)|1and|zi(t)|1in controller(9),the converted controller is as follows:

whereΞ(t)＞0,and the initial condition ofΞ(t)is consistent with that ofL3(t).

Remark 5 Evidently,by adjusting the controller parameters, the FTMLS of FCVMNNs with and without time delay can be realized, and the asymptotic synchronization of FCVMNNs with time delay can also be obtained by utilizing the comparison theorem,which extends the existing results in Refs.[33,42,43]. Hence,our results are more general and less conservative.

4. Numerical examples

To demonstrate the validity of the results,some numerical simulations are provided as follows:

Example 1 Consider FCVMNNs(2)and(3)as the driveresponse systems,wherei=1,2,3,ε=0.95,τ=0.1,the activation functionfj(sj(t))=tanh(Re(sj(t)))+itanh(Im(sj(t)))andgj(sj(t-τ)) = tanh(Re(sj(t-τ)))+itanh(Im(sj(t-τ)));I(t)=0 and

Fig.1. (a)Phase plot of the real part of drive-response systems(2)and(3)without the controller(9). (b)Phase plot of the imaginary part of drive-response systems(2)and(3)without the controller(9).

Without the controller (9), the phase trajectories of real and imaginary parts of systems(2)and(3)are shown in Fig.1.Especially,Fig.2 shows the state trajectories of real and imaginary parts of systems(2)and(3). Obviously,systems(2)and(3)cannot reach the same state in finite time,which means that systems(2)and(3)cannot achieve FTMLS.

By simple computation, we can obtainFi=Gi=1,i=1,2,3. When choose?=0.75,K=(10+7i,10+7i,10+7i)T,ξ=diag(8,8,8),ri=diag(9,9,9). Under the controller(9), the state trajectories of systems (2) and (3) are given in Fig. 3. The simulation results show that systems (2) and (3)can realize FTMLS,and the SSTT1=0.8303 is evaluated according to Theorem 1.

When?=0,τ=0.1 and the controller parameters remain the same,system(10)can converge to zero in finite time,which is shown in Fig.4(a). And the SSTT2=1.4766 is evaluated based on Corollary 1. By choosing 10 random initial conditions, the synchronization errors state can converge to zero in finite time,which is shown in Fig.4(b).

Remark 6 When we choose the same initial values conditions of systems(2)and(3)and the same controller parameters,in Ref.[43],the SSTT*can be evaluated by

Evidently, in Fig. 4(a),T2=1.4766＜T*, the result given in Corollary 1 is accurate than the result in Ref. [43]. Hence,Corollary 1 provides a more general result.

Fig.2. Under τ =0.1,? =0.75: (a)the state trajectories of the real parts of drive-response systems(2)and(3)without controller(9),(b)the state trajectories of the imaginary parts of drive-response systems(2)and(3)without controller(9).

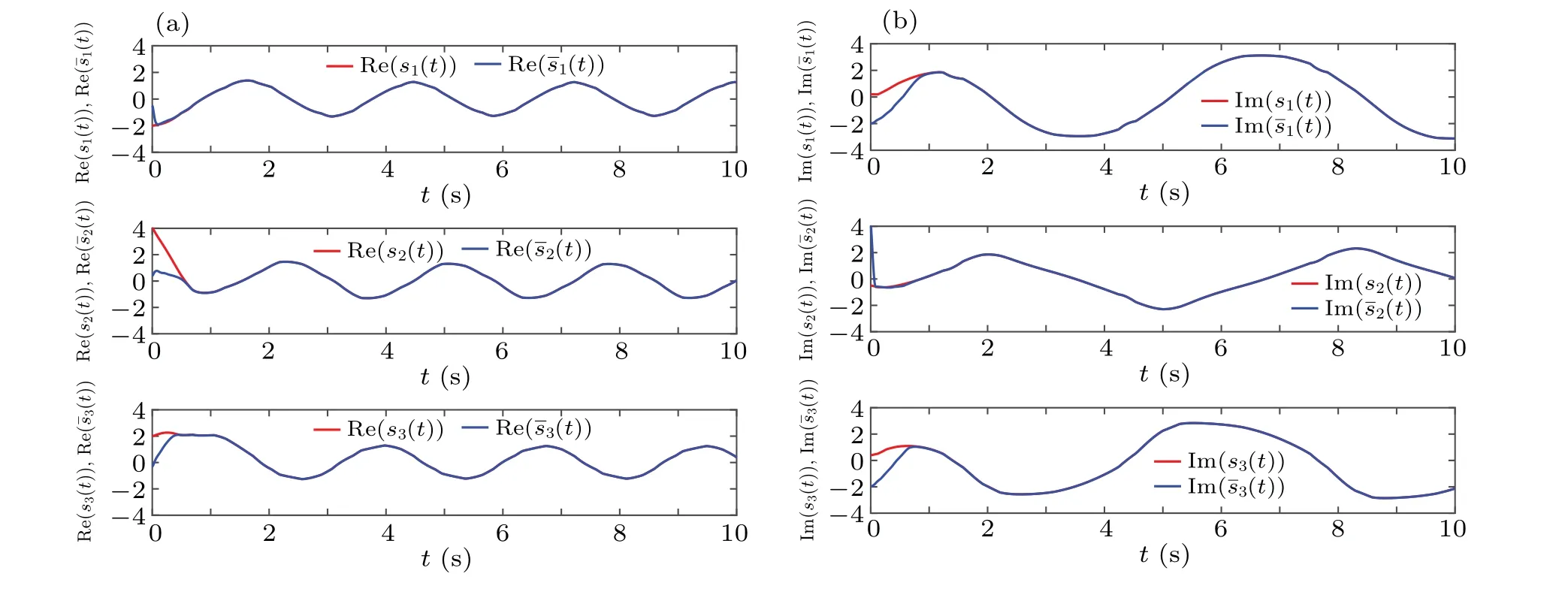
Fig.3. Under τ =0.1,? =0.75: (a)the state trajectories of the real parts of drive-response systems(2)and(3)under controller(9),(b)the state trajectories of the imaginary parts of drive-response systems(2)and(3)under controller(9).

Fig.4. Under τ =0.1, ? =0: (a) the error state trajectories under controller (28), (b) state trajectories of error system z(t)with 10 random initial conditions.

5. Conclusions

In summary, we have considered the FTMLS of a class of FCVMNNs with time delay. Different from the separation technique, we take the FCVMNNs as an entirety to analyze the system. Firstly, under the framework of Filippov solution, the original systems are transformed into the righthand continuous systems. Moreover, based on the property of complex-variable function and Lyapunov stability theorem,some sufficient conditions of FTMLS are obtained by devising a complex-valued feedback controller. Meanwhile, the upper bound of the SST can be estimated by fractional differential inequality. Compared with the results in Ref. [43],our SST is less conservative. Furthermore, by adjusting controller parameters, the global asymptotic synchronization of FCVMNNs with time delay can also be realized, which improves and enrich the results in Refs.[33,42,43]. Note that in Ref. [36], the authors focused on the application of memristive neural networks in image encryption. In the future, we will consider applications of FCVMNNs in image encryption.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.62176189 and 62106181)and the Hubei Province Key Laboratory of Systems Science in Metallurgical Process(Wuhan University of Science and Technology)(Grant No.Y202002).