Time evolution law of a two-mode squeezed light field passing through twin diffusion channels
Hai-Jun Yu(余海軍) and Hong-Yi Fan(范洪義)
1School of Materials and Engineering,University of Science and Technology of China,Hefei 230026,China
2School of Electronic Engineering,Huainan Normal University,Huainan 232038,China
We explore the time evolution law of a two-mode squeezed light field (pure state) passing through twin diffusion channels, and we find that the final state is a squeezed chaotic light field (mixed state) with entanglement, which shows that even though the two channels are independent of each other,since the two modes of the initial state are entangled with each other,the final state remains entangled.Nevertheless,although the squeezing(entanglement)between the two modes is weakened after the diffusion,it is not completely removed.We also highlight the law of photon number evolution.In the calculation process used in this paper,we make full use of the summation method within the ordered product of operators and the generating function formula for two-variable Hermite polynomials.
Keywords: two-mode squeezed light field,twin diffusion channels,time evolution law,entanglement
1.Introduction
Photon diffusion and photon dissipation are two processes in optical communications[1–4]in which decoherence usually happens.[5,6]In previous works, the diffusion and dissipation of photons have been investigated using different methods.The diffusion coefficient for photon migration should be dependent on the absorption in an absorbing medium; as a result, the absorption-dependent diffusion coefficient has been inferred from diffusion theory.[7]In addition, the evolution from a single-mode squeezed vacuum state to a squeezed chaotic state with decreasing squeezing and decoherence in an amplitude-dissipative channel has been studied.[8]Exploration has also been made of the evolution of a two-mode squeezed vacuum when it passes through a two-mode amplitude dissipative channel,with the same decay rate κ,using the continuousvariable entangled state approach.[9–12]
In this paper,we study the time evolution of a two-mode squeezed state,[13,14]which can be generated in a parametric amplifier, passing through twin diffusion channels, which means that each mode independently passes through a singlemode diffusion channel.It should be noted that a two-mode squeezed state is,itself,an entangled state,which involves the idle mode and the signal mode, so it is interesting to investigate how these modes evolve and how the photon number in these modes varies.[15–17]In the following,we make full use of the summation method within the ordered product of operators and the generating function formula of two-variable Hermite polynomials.
Theoretically,a two-mode squeezed state is expressed by

where tanhθ is a squeezing parameter anda,a?;b,b?are the two modes’photon annihilation and creation operators,which obey[a,a?]=[b,b?]=1.The density operator of a two-mode squeezed state is
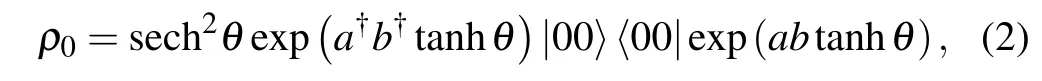
which is a pure state.To calculate thea-mode photon number(theb-mode is the same),we set

Then,from

we have
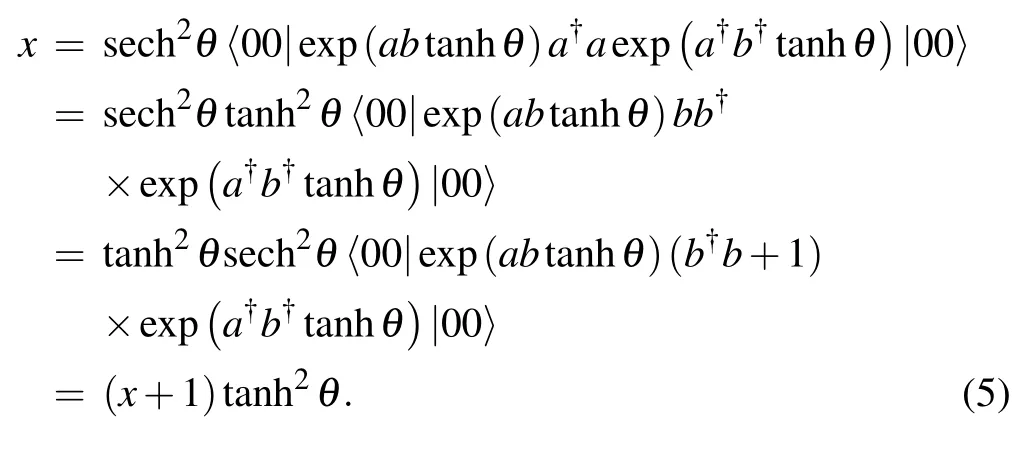
Thus,thea-mode photon number is
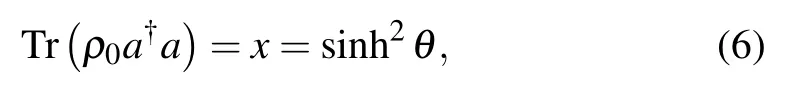
which only relies on the squeezing parameter.In the following we discuss the time evolution law of a two-mode squeezed state passing through twin diffusion channels,and we find that it evolves into a two-mode squeezed chaotic state,after which,the photon number variation can be derived correspondingly.
2.Time evolution of the density operator of a two-mode squeezed state in twin diffusion channels
It is known that the time evolution equation for a density operator in a single-mode diffusion channel is[18,19]

Here, κ is the diffusion coefficient.Using an entangled state representation[20–23]and integration within the ordered product of operators (IWOP),[24,25]we can obtain the solution in an infinitive summation form[26]
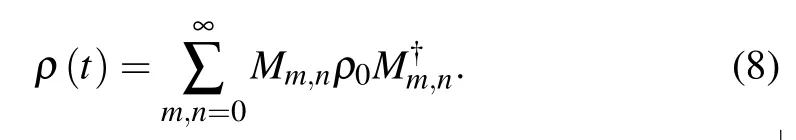
Here,ρ0is the initial density operator andMm,nis
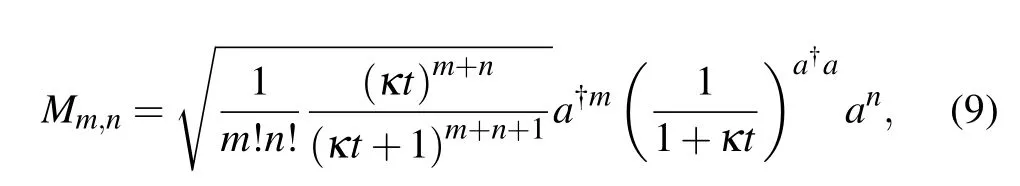
Another equation describing the evolution ofb-mode diffusion channels is
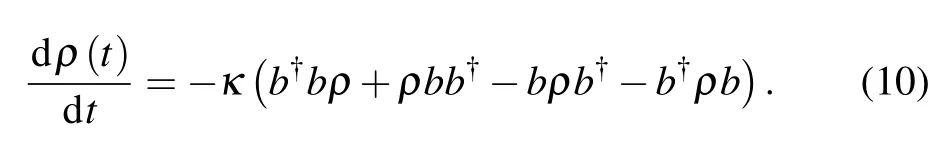
For both theamode and thebmode,the density operator solution to the diffusion equation is
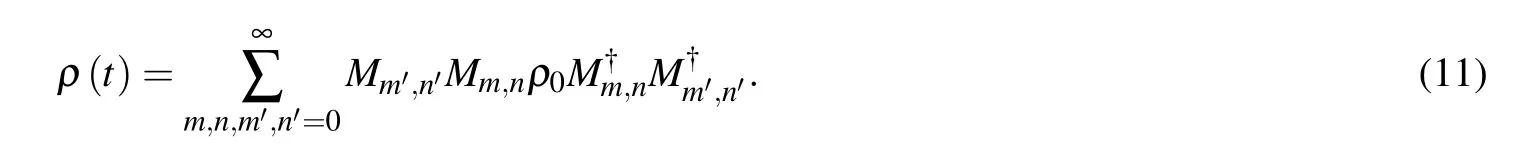
By substituting Eq.(2)into Eq.(11)and using Eq.(9),we obtain
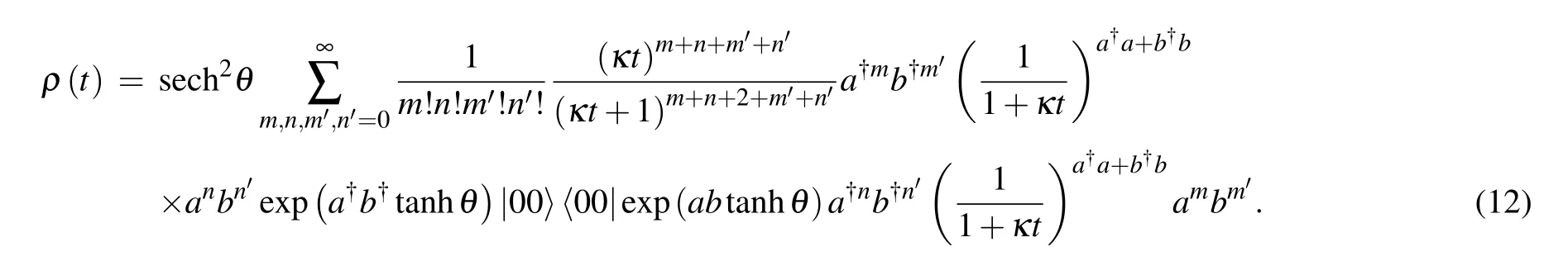
It is difficult to perform summation over the operators,since creation operators do not commute with annihilation operators.Thus, we should adopt the method of summation within the ordered product of the operators,[27,28]because within an ordered product of operators, permutation is possible.Let us first examine the part of Eq.(12)

where we have used

Due toa|z〉=z|z〉,we can employ the over-completeness relation of the coherent state= 1 and the IWOP method,which leads to

here
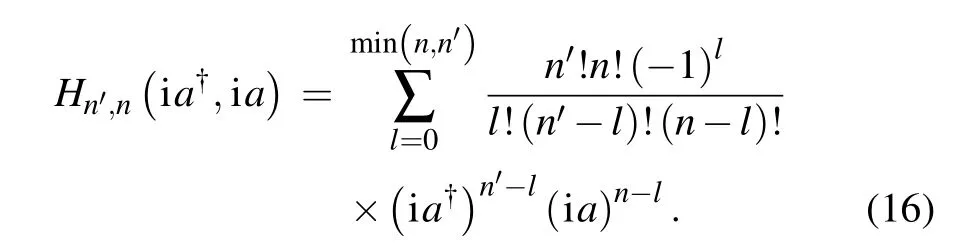

Further,using the operator identity
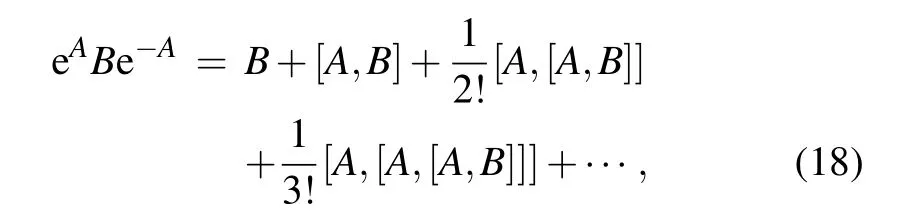
we can deal with the terms in Eq.(17)and obtain


Going back to examine ρ(t)in Eq.(12)and using
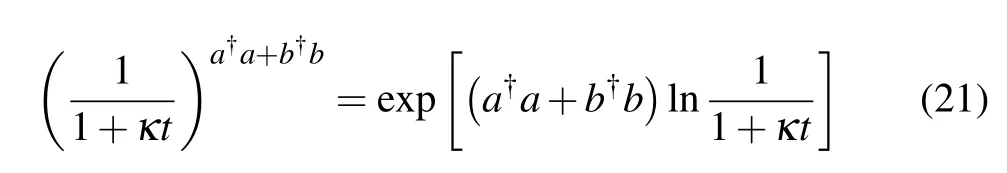
to operate on Eq.(20),we obtain
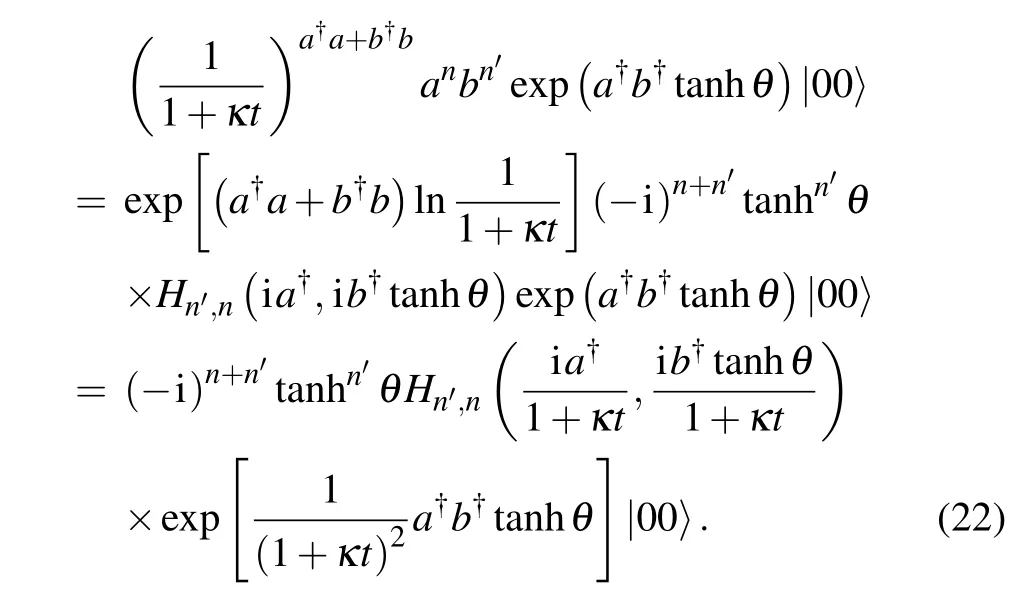
With this result and using the new generating function formula[32]forHm,n(x,y):
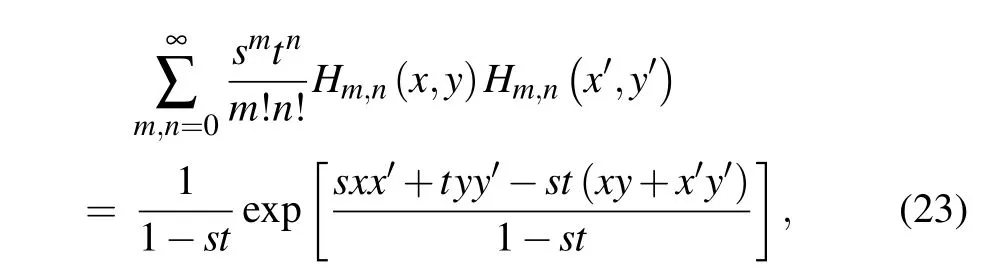
we can convert Eq.(12)into
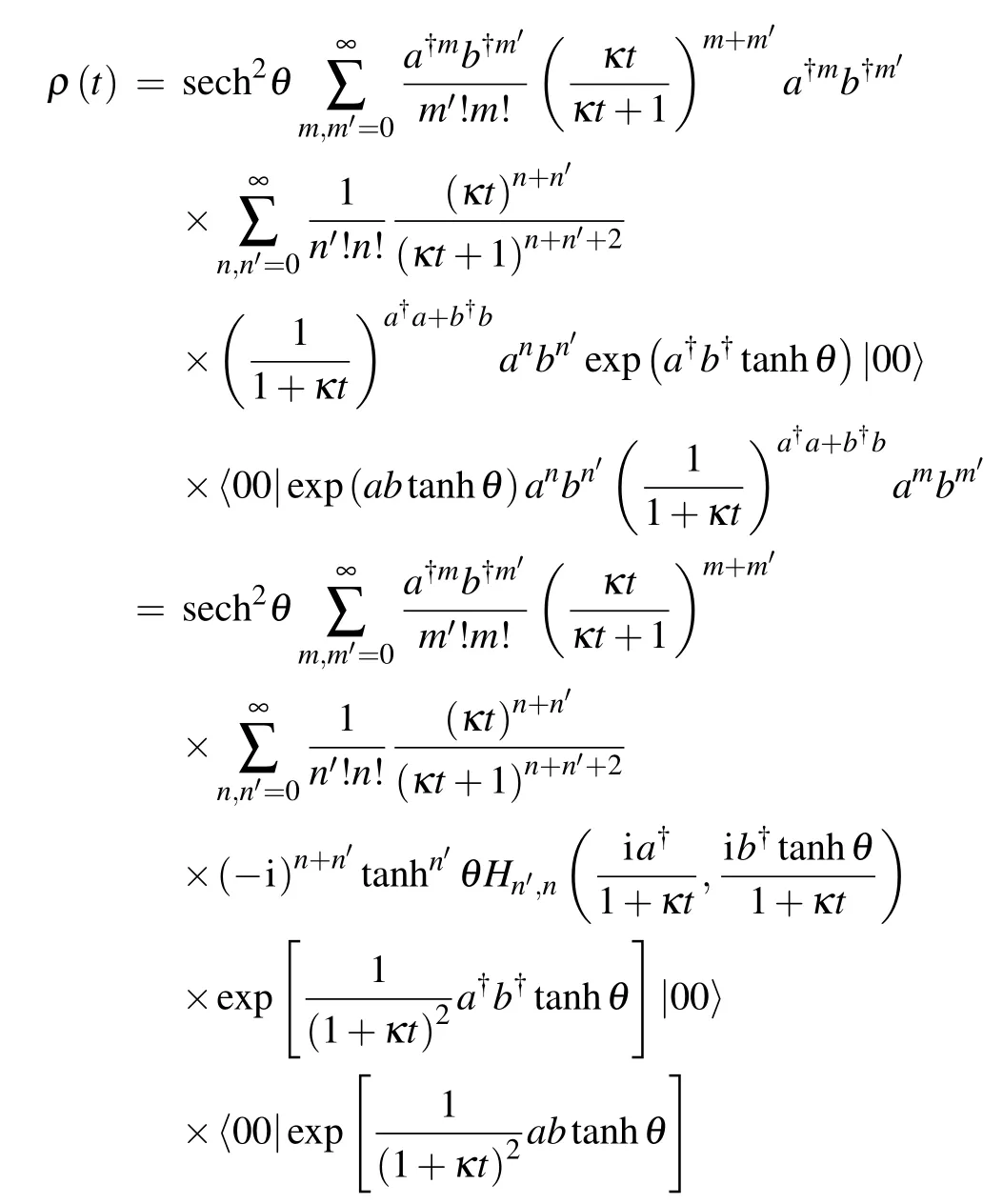
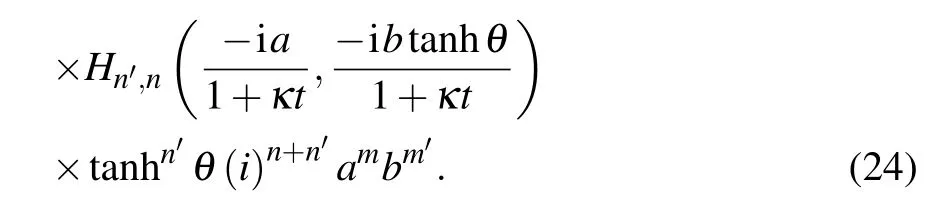
Remembering the vacuum projector |00〉〈00| =:exp(?a?a?b?b):,we see
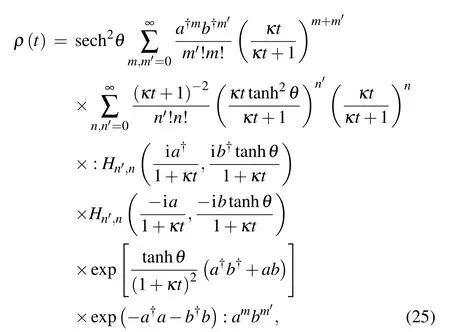
where the summation overn,n′is now within normal ordering;therefore,the creation operators can be permuted with the annihilation operators within: :,and the summation overn,n′is feasible.Using Eq.(23),we obtain

Noticing that the right-hand side is still in normal ordering,the summation overm,m′can be performed as well.The result is

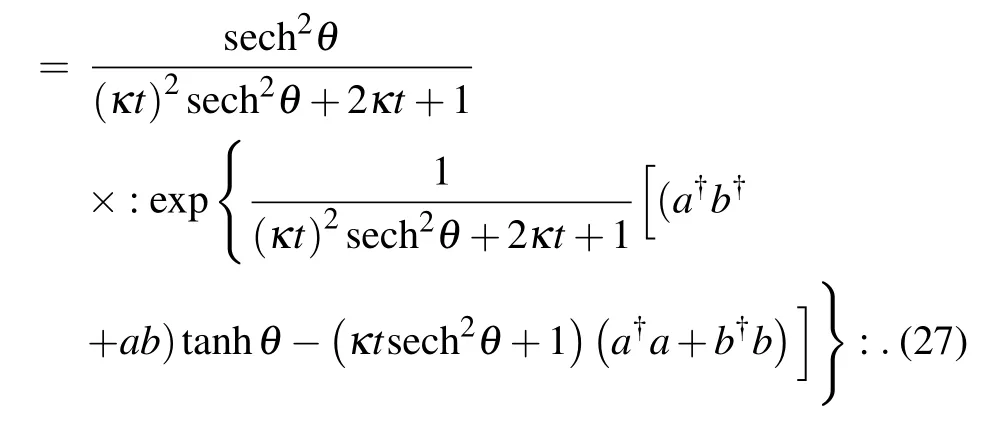
This result indicates that after passing through twin diffusion channels,the initial two-mode squeezed state ρ0(pure state) evolves into the squeezed chaotic state (a mixed state)described by Eq.(27),[33]where the exponential term involving(a?a+b?b)embodies the chaos.Clearly, whent= 0,Eq.(27)reduces to Eq.(2).
On the other hand, from Eq.(27), we can see that the original squeezing parameter tanhθ has changed to

and due to
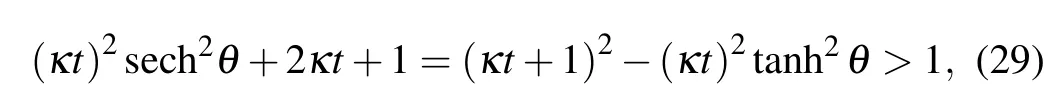
we conclude that after passing through the twin diffusion channels, the squeezing becomes weaker.Nevertheless, even though the squeezing(entanglement)between the two modes is weakened after the diffusion,the entanglement is not completely removed.
We letA=(κt)2sech2θ+2κt+1; we can now put the final density operator into a neater form
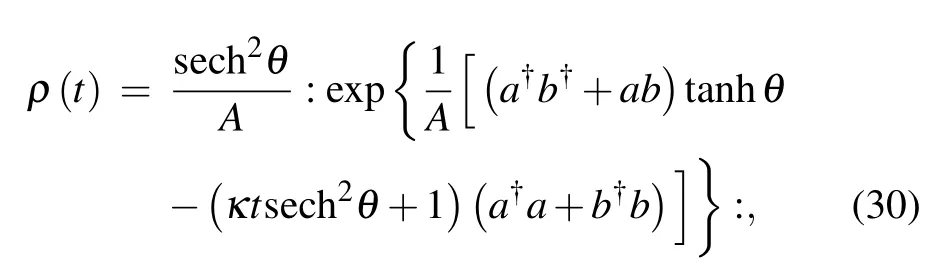
and it is necessary to check
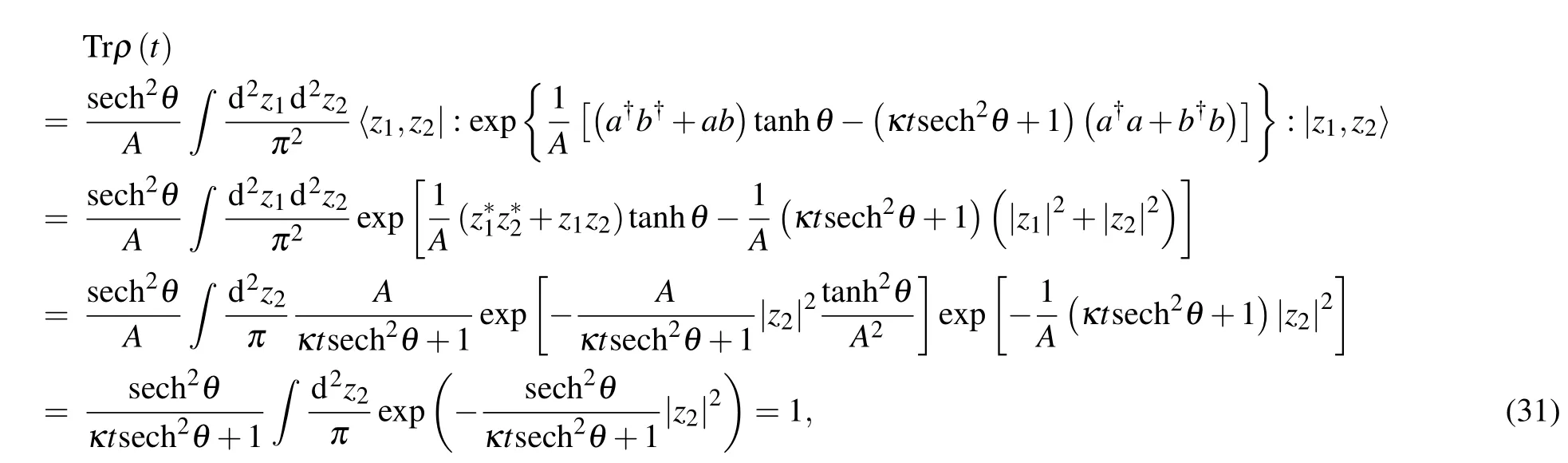
which confirms the correctness of our calculations.
3.The photon number in the final state
After performing a partial trace over thebmode for Eq.(27),we derive
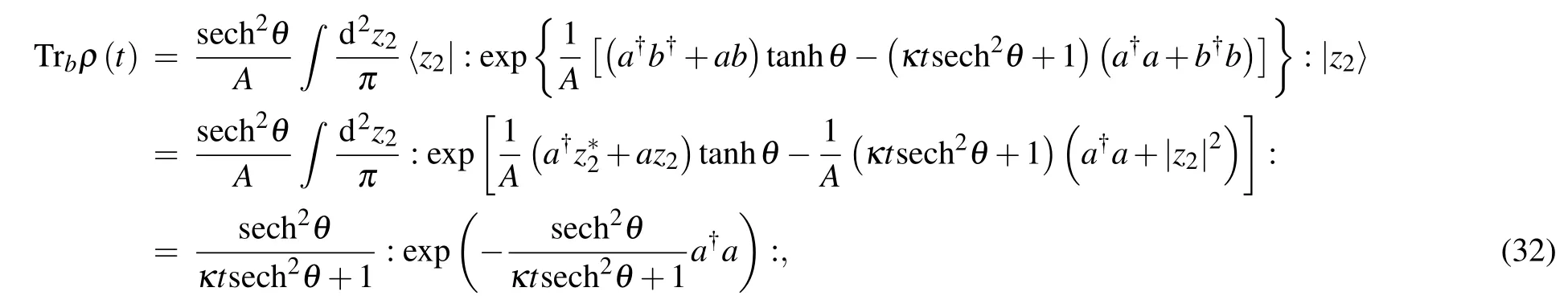
which results in a chaotic field in theamode;we then deduce thea-mode photon number in the final state
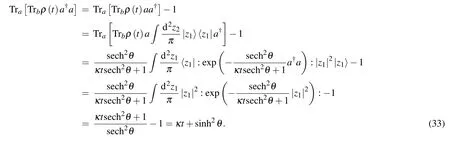
By comparison with the initial photon number in Eq.(6),we find that in the final state, thea-mode photon number has increased by an amount κt,which is proportional to the diffusion parameter.Theb-mode photon number also increases by the same amount κt.
4.Conclusion
We have discussed the time evolution law of a two-mode squeezed state passing through twin diffusion channels, and we find that it evolves into a two-mode squeezed chaotic state.The photon number in each mode increases by an amount κt.In the calculation process used in this paper,we have made full use of the summation method within the ordered product of operators and the generating function formula of two-variable Hermite polynomials.We also pointed out the law of photon number evolution.
Acknowledgments
Project supported by the National Natural Science Foundation of China (Grant No.11775208), the Foundation for Young Talents in College of Anhui Province, China (Grant No.gxyq2019077), and the Natural Science Foundation of the Anhui Higher Education Institutions of China (Grant Nos.KJ2019A0688 and KJ2020A0638).
- Chinese Physics B的其它文章
- A broadband self-powered UV photodetector of a β-Ga2O3/γ-CuI p-n junction
- High-sensitive terahertz detection by parametric up-conversion using nanosecond pulsed laser
- High efficiency,small size,and large bandwidth vertical interlayer waveguide coupler
- High-fidelity resonant tunneling passage in three-waveguide system
- An analytical model for cross-Kerr nonlinearity in a four-level N-type atomic system with Doppler broadening
- Determine the physical mechanism and source region of beat wave modulation by changing the frequency of high-frequency waves