劉麗平, 彭建文

(重慶師范大學數(shù)學科學學院, 重慶 401331)

1.引言

設(shè)H是一實Hilbert空間, 其內(nèi)積和范數(shù)分別表示為〈·,·〉和‖ · ‖,K ?H是非空閉凸集.設(shè)f:H →R∪{+∞}是一個真凸下半連續(xù)函數(shù)且T:K →2H是一個集值映射.在本文中, 我們考慮如下的集值混合變分不等式問題(簡記為SMVIP(T,K)): 求x* ∈K,且存在ω* ∈T(x*),使得

我們用Sol(T,K)表示SMVIP(T,K)的解集.

對SMVIP(T,K)的研究已經(jīng)引起了廣泛的關(guān)注.[1-5,14,17]下面各種問題可以看作是問題(1.1)的特殊情況.

顯然, 若f= 0, 則SMVIP(T,K)退化為如下集值變分不等式問題[6-8]: 求x* ∈K, 且存在ω* ∈T(x*), 使得

其次, 設(shè)φ:K →R∪{+∞}是連續(xù)凸函數(shù), 令T=?φ, 其中?φ是φ的次微分, 則x* ∈K是SMVIP(T,K)的解的充分必要條件為:x* ∈K是如下的不可微優(yōu)化問題:

的解.

當T是單值映射時,ω*=T(x*),則SMVIP(T,K)退化為如下的混合變分不等式問題[9-10]:求x* ∈K, 使得

進一步地, 若函數(shù)f= 0, 則混合變分不等式問題(1.4)就退化為經(jīng)典的變分不等式問題[11-12]: 求x* ∈K, 使得

XIA等[5]引入了一類投影次梯度方法來求解集值混合變分不等式問題(1.1), 并在T為仿單調(diào)和Lipschitz連續(xù)映射的假設(shè)條件下, 證明了由投影次梯度方法所產(chǎn)生的序列弱收斂于集值混合變分不等式問題(1.1)的解.最近, Anh和Vinh[11]在Hilbert空間中提出了一類自適應(yīng)慣性投影梯度算法來求解單調(diào)且半連續(xù)或強偽單調(diào)經(jīng)典變分不等式(1.5), 該算法的步長是動態(tài)選擇的, 且在不與混合/粘度或線搜索方法相結(jié)合的情況下, 獲得了強收斂性的結(jié)果.

因此, 為求解集值混合變分不等式問題(1.1), 我們在Hilbert空間中引入了一類新的自適應(yīng)慣性投影次梯度方法.該算法的優(yōu)點是, 步長是動態(tài)選擇的, 并且增加了慣性項以加速收斂特性.在集值映射T是f-強偽單調(diào)或單調(diào)且H-半連續(xù)的假設(shè)條件下, 我們證明了由該新算法所產(chǎn)生的序列強收斂于集值混合變分不等式問題(1.1)的解.

2.預(yù)備知識

在這一節(jié), 我們回顧或給出本文所需的定義和引理.

定義2.1[13]設(shè)T:K →2H是一集值映射.

1)T稱為閉圖象的, 如果其圖象

graph(T)={(x,y)∈K×H:x ∈K,y ∈T(x)}

是K×H中之一閉集;

2)T稱為在集合U(?K)上是緊的, 如果是H中的相對緊集.

定義2.2[14]設(shè)f:K →R∪{+∞}是一個真凸下半連續(xù)函數(shù),T:K →2H是一集值映射.則映射T稱為

1) 在K上單調(diào)的, 若對?(x,x*),(y,y*)∈graphT有:

2) 在K上仿單調(diào)的, 若T是單調(diào)的且〈y* -x*,y-x〉= 0和(x,x*),(y,y*)∈graphT可推出(x,y*),(y,x*)∈graphT;

3) 在K上強偽單調(diào)的, 若存在γ ＞0, 使得對?(x,x*),(y,y*)∈graphT有:

4) 在K上f-強偽單調(diào)的, 若存在γ ＞0, 使得對?(x,x*),(y,y*)∈graphT有:

5) 在K中的子集B上是Lipschitz連續(xù)的, 若存在L ＞0, 使得

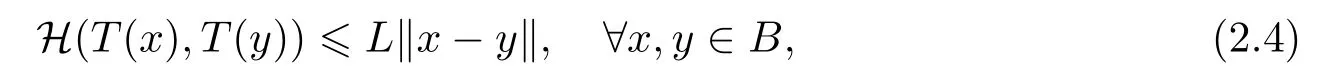
其中H(·,·)是H中的非空有界閉子集的Hausdorff度量, 即

注2.1[14]各種單調(diào)性之間蘊含關(guān)系如下:

定義2.3[15]對于一個凸函數(shù)f:H →(-∞,+∞], 我們用domf={x ∈H:f(x)＜+∞}表示其有效域, 對于給定的點x ∈domf,f在點x的ε-次微分用?εf(x)來表示, 其中

若ε=0, 則?f(x)=?0f(x)表示f在點x的次微分.

定義2.4[16]設(shè)K是Hilbert空間H上的非空閉凸子集, 則點z到K的距離定義為

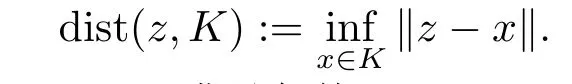
用PK(z)表示點z到K上的投影, 即PK(z)滿足條件

引理2.1[16]設(shè)K是Hilbert空間H上的非空閉凸子集, 那么有如下性質(zhì)成立:

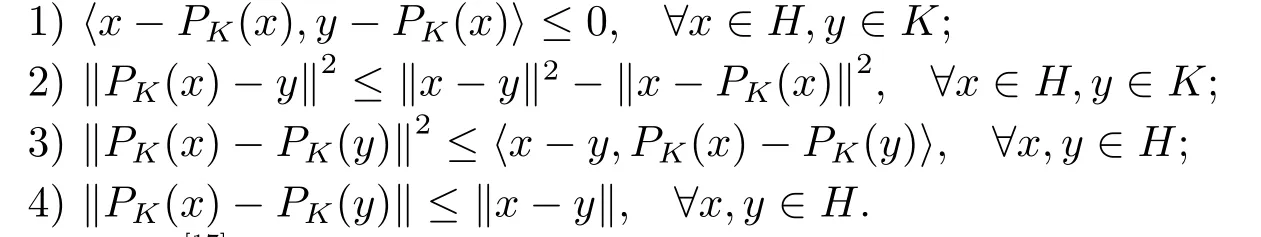
定義2.5[17]一個具有非空弱緊值的集值映射T:K →2H稱為H-半連續(xù)的, 如果對于?x,y ∈K, 函數(shù)H(T(x+t(y-x)),T(x)) : [0,1]→R+在0+處是連續(xù)的, 其中R+= [0,∞),H為Hausdorff度量.

下面的引理是文[17]中引理2.2的特殊情形.

引理2.2[17-18]設(shè)f:H →R∪{+∞}是一個真凸下半連續(xù)函數(shù),T:K →2H是具有非空弱緊值的H-半連續(xù)且單調(diào)的集值映射, 則對于x* ∈K, 下面兩個式子等價:

3.算法及其收斂性分析

下面將介紹一種求解f-強偽單調(diào)或單調(diào)集值混合變分不等式問題(1.1)的自適應(yīng)慣性投影次梯度方法.在我們的研究中, 需要使用下面的條件:

(A1)T是f-強偽單調(diào)映射;

(A2)T是具有非空弱緊值H-半連續(xù)且單調(diào)映射;

(A3)T在有界集上是有界的;

(A4) Sol(T,K)?;

(A5)f:H →R∪{+∞}是一個真凸下半連續(xù)函數(shù)且K ?int(domf),?εf在K上是有界.

算法設(shè)計如下:

算法A(SMVIP(T,K)的自適應(yīng)慣性投影次梯度算法)

步0 取初始點x0∈K,v0∈T(x0),θ ∈[0,1), 令k:=0.

步1 若0∈T(xk)+?f(xk), 則停止; 否則執(zhí)行步2.

步2 選擇αk, 使得其中

計算

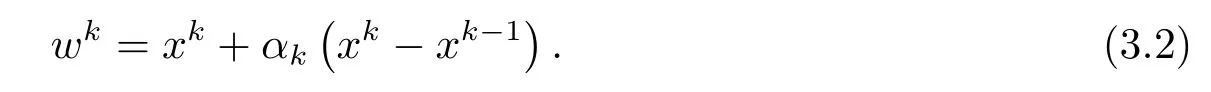
取uk ∈?εkf(xk),ηk=max{1,‖vk‖+‖uk‖}, 計算

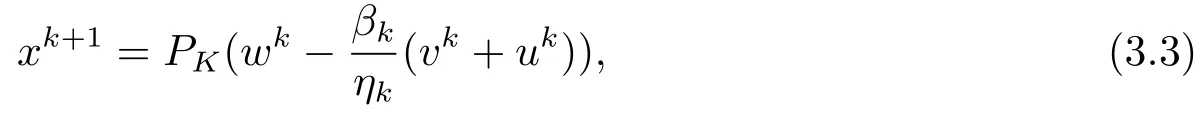
其中

步3 取vk+1∈T(xk+1), 使得

令k=k+1并轉(zhuǎn)回步1.

注3.1若我們?nèi)ˇ? 0, 從而= 0,αk= 0, (3.2)式變成wk=xk, (3.3)式變成xk+1=則此時算法A即為文[5]中的投影次梯度算法.

注3.2若T是單值映射, 則我們可以計算vk+1=T(xk+1), 則步3中的(3.5)式自然成立.

注3.3在步2中(3.2)式采用慣性技術(shù), 將投影方法與步長規(guī)則相結(jié)合.

引理3.1設(shè)序列{xk}是由算法A生成的, 則對?z ∈K, 有下面的不等式成立:

證由φk的定義有

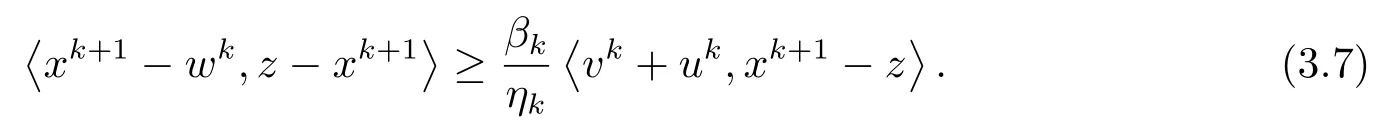
結(jié)合(3.6)和(3.7), 我們有

另外

由(3.8)和(3.9)有

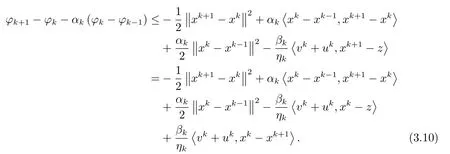
利用Cauchy-Schwarz不等式和均值不等式有

以及

因此, 結(jié)合(3.10), (3.11)和(3.12)有

故結(jié)論得證.

下面分析由算法A所生成序列{xk}的收斂性.

定理3.1若由算法A所生成的序列{xk}只有有限個元, 則xk是SMVIP(T,K) 的解.

證若序列{xk}只有有限個元, 則對于某個xk, 算法A將在步1處停止.從而, 0∈T(xk)+?f(xk), 故存在ω ∈T(xk), 使得-ω ∈?f(xk).由次微分的定義知:

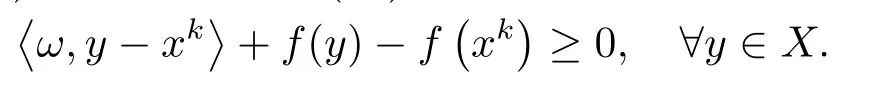
從而,xk是SMVIP(T,K)的解.

下面, 我們假設(shè)由算法A所產(chǎn)生的序列{xk}有無窮多個元.

定理3.2假設(shè)條件(A1), (A3), (A4)和(A5)成立, 則由算法A生成的序列{xk}強收斂于SMVIP(T,K)的唯一解.

證由假設(shè)(A1)知T是f-強偽單調(diào)的, 這表明SMVIP(T,K)的解具有唯一性.

事實上, 設(shè)x1,x2∈Sol(T,K), 且分別存在ω1∈T(x1),ω2∈T(x2), 使得

和

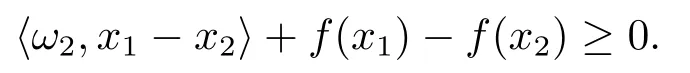
由T的f-強偽單調(diào)性可得, 存在γ ＞0, 使得

結(jié)合(3.13)和(3.14)可得

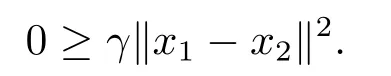
因此x1=x2.

現(xiàn)在設(shè)x* ∈Sol(T,K), 由引理3.1可得

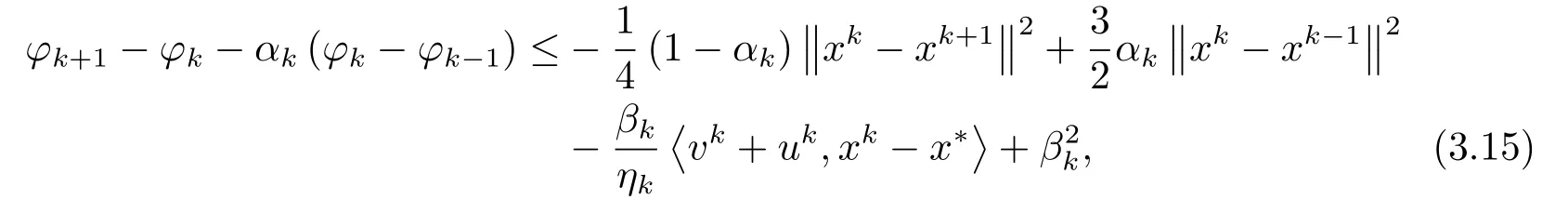
因為uk ∈?fεk(xk), 則有

從而

將(3.16)代入(3.15)中有

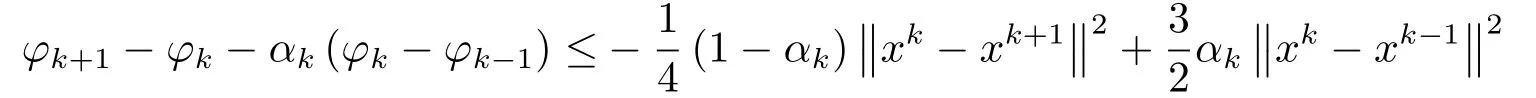
因為x* ∈Sol(T,K), 且存在ω* ∈T(x*), 使得

又由T的f-強偽單調(diào)性知, 存在vk ∈T(xk), 使得

從而(3.17)化簡得

利用引理2.4, 令

將(3.18)代入(3.19), 再利用φk的定義有

由前面的證明知序列xk有界.設(shè)B是包含xk的一個有界集, 且ˉε=sup{εk}.則

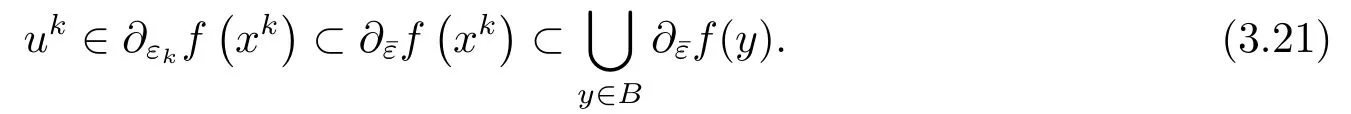
由(3.21)和假設(shè)(A3),(A5)知,序列uk和vk都有界,則存在ρ ＞1,使得對所有的k,有≤ρ.從而

則

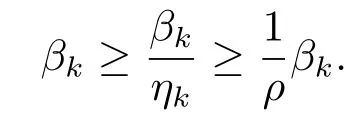
再結(jié)合(3.4)得

即{xk}強收斂于SMVIP(T,K)的唯一解.

注3.4與文[11]的算法不同的是, 本文將文[11]針對經(jīng)典變分不等式問題的算法推廣到集值混合變分不等式問題.定理3.2在T為f-強偽單調(diào)條件下, 證明了該算法的強收斂性.而文[5]的定理3.5在T是仿單調(diào)的情況下證明了算法3.1的弱收斂性.

當算法A中的θ=0時, 我們可以得到如下的算法B.[5]

算法B(SMVIP(T,K)的投影次梯度算法)

步0 取初始點x0∈K,v0∈T(x0),θ ∈[0,1), 令k:=0.

步1 若0∈T(xk)+?f(xk), 則停止; 否則執(zhí)行步2.

步2 取uk ∈?εkf(xk),ηk=max{1,‖vk‖+‖uk‖}, 計算

其中

步3 取vk+1∈T(xk+1), 使得

令k=k+1并轉(zhuǎn)回步1.

接下來我們分析由算法B所生成的序列{xk}的收斂性.

定理3.3假設(shè)條件(A2)-(A5)成立,則由算法B所生成的序列{xk}弱收斂于SMVIP(T,K)的一個解.

證當θ=0 時, 則αk==0, 利用引理3.1, 對?z ∈K, 有

再利用φk的定義有

則

因為uk ∈?fεk(xk), 則有:〈uk,xk-z〉≥f(xk)-f(z)-εk, ?z ∈K.

則

從而

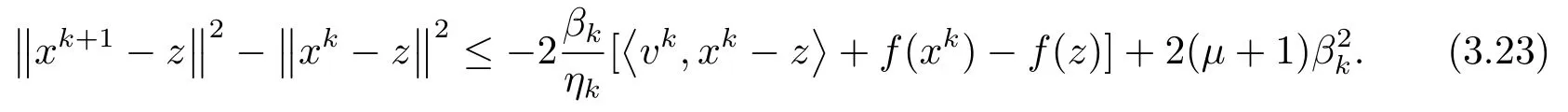
若z ∈Sol(T,K), 且存在ω ∈T(z), 使得

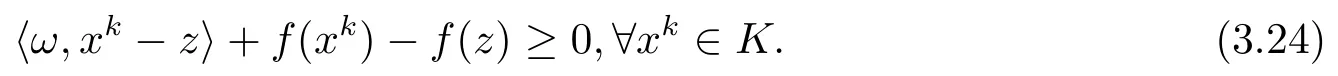
由于T是單調(diào)的, 則對ω ∈T(z),vk ∈T(xk)有

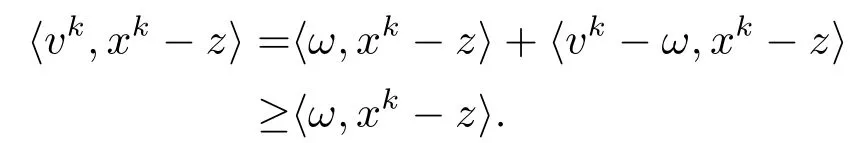
將上式代入(3.23)得

將(3.24)代入(3.25)有

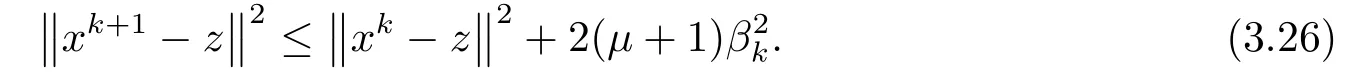
這表明序列{xk}關(guān)于Sol(T,K)是quasi-Fejr收斂.由引理2.3中1)知,{xk}有界.

先證明{xk}的所有弱聚點屬于Sol(T,K).設(shè)是{xk}的弱聚點, 則存在{xk}的子列{xkj},有:xkj ?

將(3.25)整理后有

在(3.27)用kj取代k有

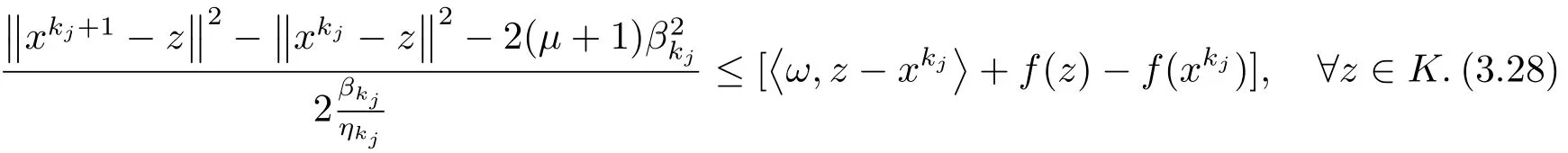
由假設(shè)(A2), (A5)和引理2.2知, 上式等價于

注3.5在定理3.3中, 假設(shè)條件(A2), (A3)與文[5]的假設(shè)(A3)(即:T是具有有界凸值的仿單調(diào)映射, 使得T是弱閉且在H的有界子集上是Lipschitz連續(xù))相比,T是不需要Lipschitz連續(xù)性, 其中文[14]中的例3說明了我們的假設(shè)(A1), (A3)的合理性.

注3.6在定理3.3中,T是單調(diào)映射, 文[5]要求T是仿單調(diào)映射, 兩者的關(guān)系見注2.1.

下面我們增加假設(shè)條件: Sol(T,K)的內(nèi)部非空, 可獲得{xk}的強收斂性.

定理3.4假設(shè)條件(A2)-(A5)成立且int Sol(T,K)?, 則由算法B生成的序列{xk}強收斂于SMVIP(T,K)的一個解.

證由定理3.3知{xk}有界, 則存在R ＞0, 使得對?k, 有‖xk‖≤R.定義序列{zk}:

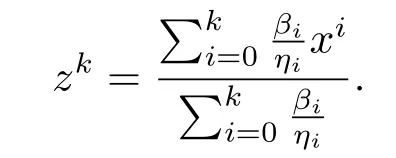
由于f是凸函數(shù), 則有

從而

故化簡不等式(3.30)得

上式用kj取代k有

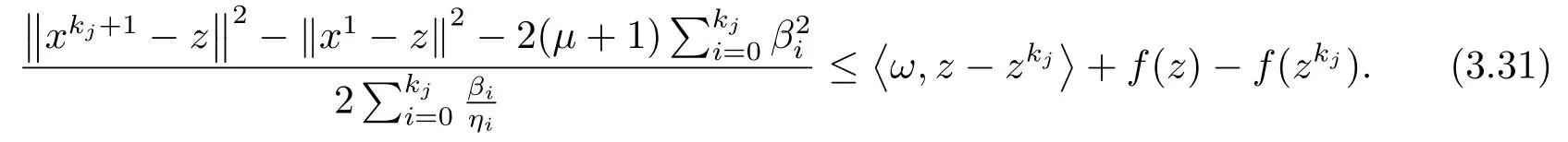
注3.7定理3.4證明了由算法B生成序列的強收斂性, 而文[5]的定理3.5只獲得了弱收斂的結(jié)果.

4.結(jié)論

本文是針對在實Hilbert空間中的集值混合變分不等式問題, 對之前學者提出的投影次梯度算法以及結(jié)果進行了適當?shù)母倪M, 引入一類新的自適應(yīng)慣性投影次梯度算法, 在合適的假設(shè)條件下, 證明了該算法的強收斂性.