On the performance of full-duplex non-orthonogal multiple access with energy harvesting over Nakagami-m fading channels①
Guo Weidong(郭衛(wèi)棟),Zheng Dong
(*School of Information Science and Engineering,Shandong University,Qingdao 266237,P.R.China)
(**School of Cyber Science and Engineering,Qufu Normal University,Qufu 273165,P.R.China)
Abstract
Key words:non-orthogonal multiple access(NOMA),full-duplex(FD),energy harvesting(EH),Markov chain
0 Introduction
As one of the promising key techniques of the fifth generation(5G) wireless networks,non-orthogonal multiple access(NOMA)has been applied in various areas[1-2].NOMA utilizes the power domain to achieve multiple-access strategies,which is unlike the conventional orthogonal multiple access(OMA)structures.Since the NOMA technique exploits the new dimension of the power domain,it has the potential to be integrated with existing MA paradigms.On the other hand,the technique of cooperative transmission can form a virtual multiple-input multiple-output(MIMO)scheme to process data cooperatively,which can enhance the communication reliability for the users who are in poor channel conditions.It is reasonable to integrate NOMA into relaying networks.Ref.[3]proposed a new cooperative NOMA scheme and analyzed the outage probability and diversity gain of the system.In Ref.[4],it is revealed that cooperative NOMA achieves the same diversity order and the superior coding gain compared to cooperative OMA.
To avoid additional bandwidth cost for cooperative NOMA system,full-duplex(FD)has attracted considerable attention,because transmission and reception are performed simultaneously on the same carrier frequency in FD operation[5].Two main types of FD relay techniques,namely FD amplify-and-forward(AF)relaying and FD decode-and-forward(DF)relaying,had been discussed in Refs[6-8].The outage probability of FD-AF relaying with a non-negligible direct link was analyzed in Ref.[6],which considers the processing delay of relaying in practical scenarios.Ref.[7]analyzed the outage probability of a basic three-node FDAF relaying system.Ref.[8]characterized the outage performance of FD-DF relaying and demonstrated that it is possible to determine which duplex mode is superior under the target outage probability.
Another goal of 5G networks is to maximize the energy efficiency.Therefore,energy harvesting(EH),a technique to harvest energy from radio frequency signals,has received considerable attention as a solution to overcome the bottleneck of energy constrained system[9].Recently,relays with EH capabilities have attracted lots of research interests,where the relay can use the energy harvested from the other nodes to perform the data forwarding[10].This can solve the problem of the energy supply of relays and expand the application of EH-based wireless communications.Ref.[11]investigated a dual-hop cooperative communication system,where source node communicates with destination node through direct and EH relaying paths.Ref.[12]addressed energy efficiency-spectrum efficiency trade-off in an EH cooperative cognitive radio network operated in a frame structure comprising of spectrum sensing and cooperation-transmission mode.Nevertheless,the amount of energy harvested from RF radiation is often restricted and it is desirable for relays to accumulate the harvested energy in the energy storage such as super-capacitors or rechargeable batteries[13].In Ref.[14],different from the conventional battery-free EH relaying strategy,harvested energy is prioritized to power information relaying while the remainder is accumulated and stored for future usage with the help of a battery in the proposed strategy,which supports an efficient utilization of harvested energy.
In order to improve the spectral efficiency and energy efficiency,the FD-NOMA relaying for the downlink transmission over Nakagami-mfading channels is considered and a comprehensive performance analysis is provided.The analysis of this paper provides more general results,as the Nakagami-mfading can incorporate the most commonly used Rayleigh fading and Rice fading as special cases,which can be obtained by adjusting the fading parameter.The main contributions of this paper are summarized as follows.
(1)This paper studies a NOMA-based downlink FD-AF relaying network over Nakagami-mfading channels.The relays have no other energy supplies,but they are equipped with chargeable battery and can harvest and store the wireless energy broadcasted by the source.Based on this structure,a new relay selection scheme is proposed considering both the channel state information(CSI)and the battery statuses of relays.
(2)This model combines NOMA,cooperative communication,FD and EH together reasonably and can improve spectral efficiency and energy efficiency simultaneously.
(3)The amount of energy stored in the battery of each relay is modeled as finite states and a finite Markov chain is used to model the variation of energy at each relay.Both the transition probability and the steady-state probability are derived for the next performance analysis.
(4)The asymptotic expressions of outage probability and the ergodic sum-rate for both near and far users are derived.Finally,simulation results are presented to validate the theoretical analysis and verify the superiority of FD-NOMA relaying over the traditional HD-NOMA relaying and OMA relaying.
This paper is different from the recent work[15].The main differences between them are summarized as follows.
(1)The models of two papers are quite different.In Ref.[15],the model is very simple.The source has no direct link with users.The channels are assumed to follow Rayleigh fading and relays operate in half-duplex mode.In this paper,the source has direct link with users and the channels are assumed to follow Nakagami-mfading which is more accorded with actual communication scenarios.In addition,relays in this paper operate in full-duplex mode which improves the spectral efficiency.
(2)In Ref.[15],the source transmits information to all users simultaneously using NOMA scheme.While in this paper,2-user NOMA is used.In general,2-user NOMA is a typical scenario,where two of all users are selected to perform NOMA.The decoding complexity and delay at the receivers are lower and shorter compared with all-user NOMA.
(3)In Ref.[15],only outage probability is analyzed,while in this paper,both outage probability and ergodic sum-rate are analyzed.
The rest of this paper is organized as follows.System model is introduced in Section 1.The relay selection scheme is illustrated in Section 2.The closed-form expressions of outage probability and ergodic sum-rate are derived in Section 3.Numerical and simulations results are presented in Section 4 and conclusions are drawn in Section 5.
1 System model
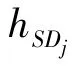
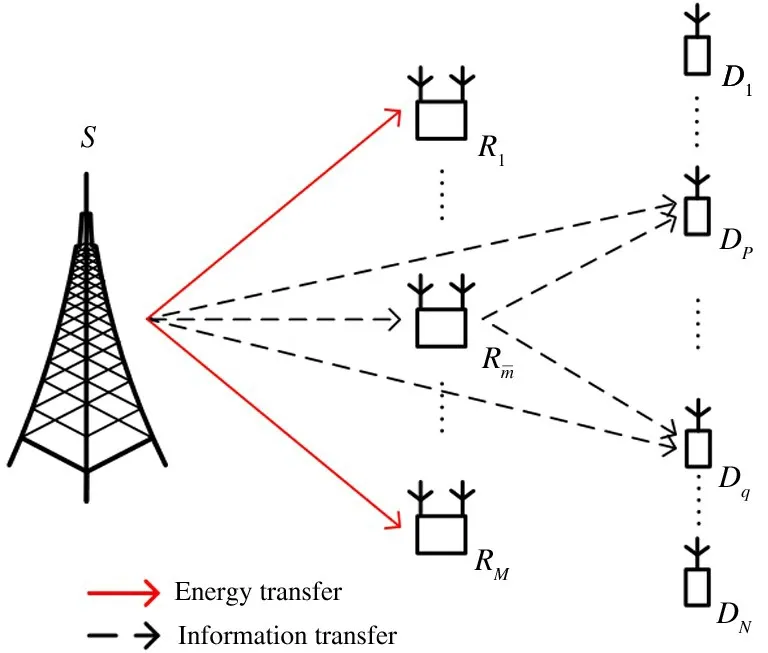
Fig.1 A reference model for multi-relay cooperative FD-NOMA network
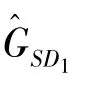
AF-NOMA protocol is used for downlink transmission and a normalized unit block time(i.e.,T=1)is considered.Before the transmission,each relay judges if it has enough energy to forward the information.If the relay does not have enough energy,it performs EH in this time block and stores the harvested energy into its battery.The amount of energy harvested from the source can be expressed as

where,PSis the source power,ηis the energy harvesting efficiency at each relay.
For those relays with sufficient energy,they report their CSI toSfor the relay selection decision.Lettingωidenote the amount of energy in the battery of relayRi,relays with enough energy are defined as the eligible set
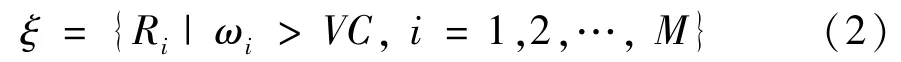
where,Cis the energy harvesting threshold to activate the EH circuit,Vis a positive integer.If the selected relay for forwarding data is assumed to have the same transmitting power asS,Vmust satisfy
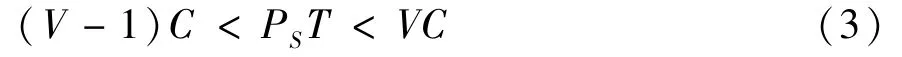
Among this set of relays,Rˉmis selected,which can be expressed as


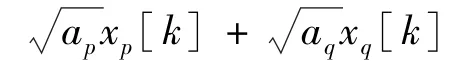
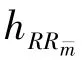
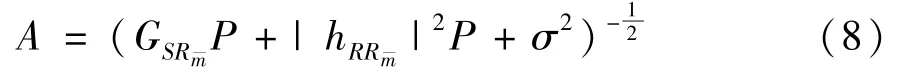
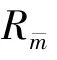

Using selection combining(SC),the instantaneous SINR ofDpcan be obtained as
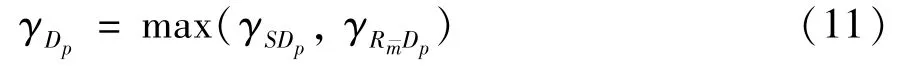
As forDq,the successive interference cancellation(SIC)is applied to decode information ofDp.Particularly,Dqfirst decodes the message ofDp,then subtracts this component from the received signal to detect its own information.Therefore,the received SINRs atDqfor the decoding of the information ofDpare given by

After SIC operation,the instantaneous SINRs atDqfor the decoding of its own information are expressed by

Similar to Eq.(11),according to the SC,the instantaneous SINR ofDqcan be expressed as
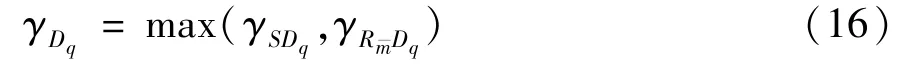
2 Relay selection rule
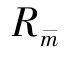
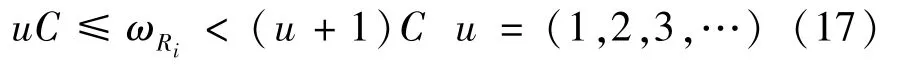
This assumption is closer to the practical scenario,and the evolution of the battery status of each relay can be modeled as a finite-state Markov chain.Using the transition probability matrix of this chain,the steady state probability vector which can be used for analyzing the performance can be got.
The above analysis is computationally intense whenMis large.To facilitate the computation,an approximated approach based on two simplified assumptions is proposed.Firstly,the relay energy amount at the selection epoch is denoted as a random variableZ.To ease the computation,Zis approximated as a uniform random variable over[0,BC].This approximation is inspired by considering the amount of harvested energy in a transmission block follows the geometric distribution with parameter 1/2[18].The effectiveness of the assumption will be discussed in the simulation part.Secondly,it is easy to find that each relay may be either short of enough energy to participate in relay selection or otherwise,so the evolution of relay energy amount is captured by using two states,either active or inactive.With this two-state Markov chain,a relay is ins0if the relay lacks sufficient energy to transmit,or ins1when the relay has enough energy for transmission.Next,how to obtain the transition probability matrix of this two-state Markov chain will be discussed.
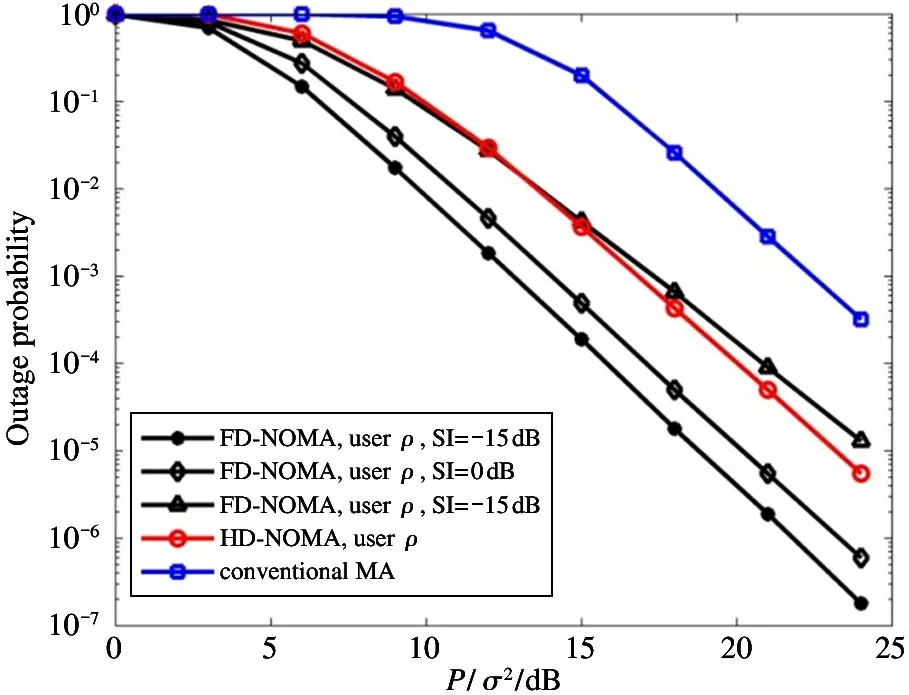
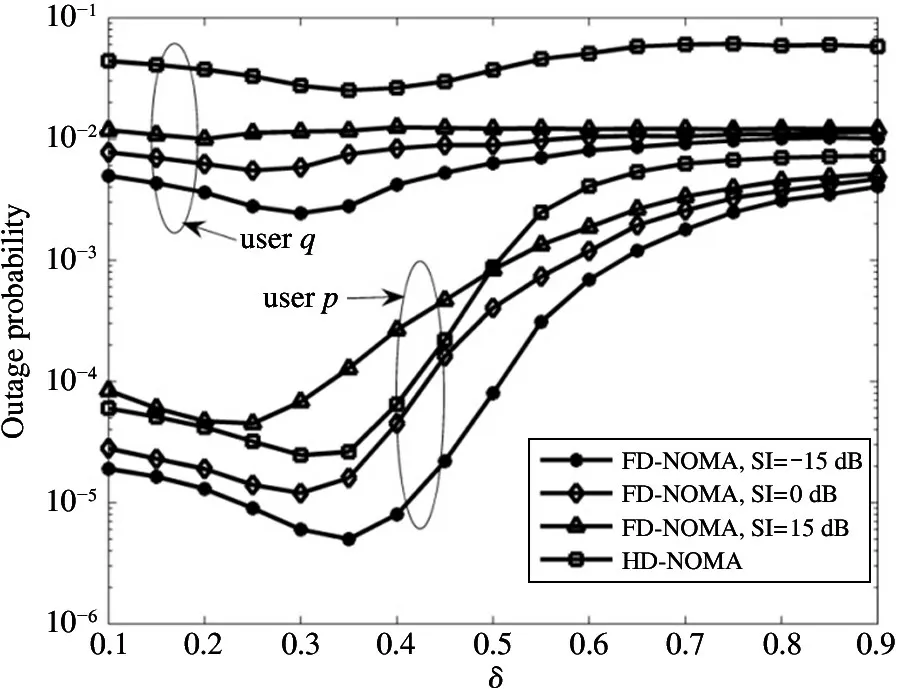
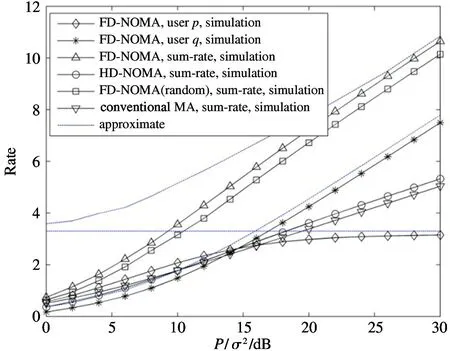
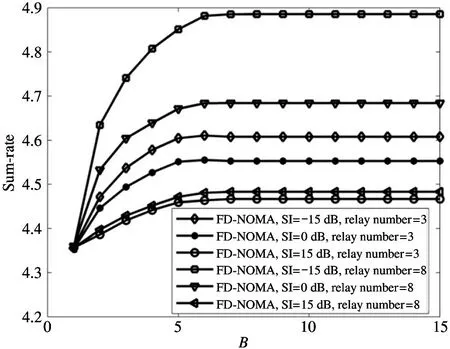
The transition froms0tos0happens when a relay has no enough energy to transmit(i.e.,Z whereΓ(·)is Gamma function[19].The corresponding cumulative distribution function(CDF) is expressed by Ifm1takes positive integer value,then with the help of Ref.[19],Eq.(18)can be solved as The transition froms0tos1happens when the relay enters the EH mode in the current bock and the accumulated energy exceedsVC.Hence, Similar to the derivation of Eq.(22),Eq.(25)can be obtained. The transition froms1tos0happens when the relay with enough energy is selected as the best relay for transmitting and its remaining energy is not enough for another transmitting.Hence,the transition probability is given by Using this PDF,the first term in the right of Eq.(26)can be obtained as As to the second term,it is noted that the i.i.d.fading assumption implies each relay inξhas an equal chance to be selected as the best relay.To simplify the analysis,the cardinality ofξis approximated by its mean such that The transition probability froms1tos1can be solved in the similar manner as the previous case,so the derivation is omitted. When the two-state Markov chain is formulated,the steady-state probability vector can be easily obtained as It should be noted that bothv0andv1involveP1,0,which is a function ofv1.By substitutingP0,1andP1,0into Eq.(31),v1can be solved explicitly.Taking the condition 2VC Withv1at hand,Pr(|ξ|=Ω)(Ω=1,2,3,…)can be got which follows the binomial distribution with the probability mass function given as According to the total probability law,the outage probability ofDporDqcan be written as The scheme would be in outage if the SINR falls below the pre-set threshold,so the outage probability of terminalDpis given by whereτ=γthp/γ(ap-aqγthp).It is noteworthy that Eq.(38)exists if and only ifγthp Next,the analysis of an outage event atDqis presented.Owing to the mechanism of SIC,the outage probability ofDqis given in the following. whereγthqis the threshold ofDq.J3can be expanded as Next,according to Eqs(13)and(15),J4can be written as The derivation of the integral in Eq.(43)is the same as Eq.(39),so it is omitted here.So far,the outage probability ofDqhas been derived by substituting Eqs(33),(42)and(43)into Eq.(34). In this section,the ergodic sum-rate for a pair of users is analysed which is given by The rate ofDpcan be calculated in the following,where approximation is attained under the condition ofγ→∞. All probabilities in the Eq.(46)can be got according to the above analysis.OnlyJ5,J6andJ7need to be derived in the following.Firstly,J5can be written as Using Eq.(37),Eq.(3.351.2)of Ref.[19]and Eq.(3.353.5)in Ref.[19],the close form ofJ5can be got as Now denoting the random variable: Thus an upper bound ofJ6is rewritten as Thirdly,J7can be rewritten as As the derivation process of Eq.(49),denoting the random variable Then,Eq.(53)can be written as In this section,Monto-Carlo simulations are performed to validate the theoretical analysis.In all simulations,the energy conversion efficiencyη=0.5,the fixed transmission rate of the source is 1 bit per channel use(bpcu).Cis set as the multiple of the source transmission energy,i.e.,C=δPT,whereδ>0 is the scaling factor.To facilitate the analysis,the following sets of parameters are used:N=3,σ2=1,m0=m1=m2=2,ΦSD=ΦSR=ΦRD=1,ap=8/9,aq=1/9,γthp=1 dB,γthq=2 dB,p=1,q=3. Fig.2 shows the performance of the proposed scheme and existing schemes versus the transmitting SNR of source.One relay is sleceted randomly from the eligible relay set when the FD-NOMA(random)scheme is used.It can be seen that the approximate analysis of finite Markov chain is accurate in the whole SNRs.Compared with the HD-NOMA,FD-NOMA(random)and conventional OMA relaying scheme,the outage behavior of each terminal in the FD-NOMA relaying system is better,even in the existence of SI at the relay.It can also be found that the diversity order for each user in the proposed shceme is equal to that in the HD cooperative NOMA system.Since the theoretical analyses agree well with the simulations,only analytical results will be plotted in the remaining outage probability figures. Fig.2 Outage probability with different user and scheme In Fig.3,the impacts of SI on the outage probability are investigated.It can be seen that the outage performance of the FD relaying(only take one user,e.g.,Dp,and vice versa)system will become worse than that in the HD relaying network for high-SNR values when SI is extremely severe.But both two schemes can have better outage performance than the conventional OMA scheme and spectral efficiency can be improved in the FD-NOMA system. Fig.3 Outage probability with different SI In Fig.4,the impacts ofδon the performance of the proposed scheme with different SI in medium SNR conditions(P/σ2=20 dB)are illustrated.For all the curves,the trends are the same for all schemes,namely,the probability first decreases then increases asδvaries from 0 to 1.This means that,when the other parameters are determined,there must be an optimal value ofδ.However,the values of the inflection points are not always the same for different users and SI.It can be seen that for the user with better channel condition(Dq),the optimal value is smaller than user with worse channel condition(Dp).This is becauseDphas the worse direct link,so it needs more power to enhance the relay link.It can also be seen that for the FD cooperative NOMA system,the optimal value shifts to the left with the increase in the level of SI and whenδis too big,the outage behavior is nearly the same under different values of SI.Compared to the HD cooperative NOMA system,the outage behavior ofDpis getting inferior when the value of SI is large andδis small.Finally,the optimal value ofδcan easily be obtained by a one-dimensional exhaustive search.With this optimal value ofδ,the system can resist fading more effectively.high-SNR regions,we will only plot the analytical results in the remaining rate figures.Secondly,the results clearly show that the FD-NOMA system can achieve a larger sum-rate compared with the HD relaying system,FD-NOMA(random)and conventional OMA system,but twice as much as HD-NOMA cannot be achieved owing to the effect of SI.More importantly,with the increase of system SNR,the rate ofDpapproaches a certain value,whereas theDqcan obtain improved performance.Both the two conclusions are consistent with the derivations in Eq.(45)and Eq.(46). Fig.4 Outage probability againstδ(M=6,B=10) Fig.5 Rate with different user and different scheme In Fig.6,the impact of battery size on the proposed finite battery scheme is investigated by varying the relay number and SI.It can be observed that the performance increases asBor relay number increase.However,the gain provided by a larger battery size does not increase whenBexceeds a certain value and this value is approximate to 6.From this figure,it can also be seen that the battery can not offer enough energy for forwarding the data whenB=1,so the performances are the same for all curves and the performance gap for different SI increases as the number of relay increases. Fig.6 Sum-rate against B(δ=0.5) A relay selection scheme for the FD-NOMA networks with EH over Nakagami-mfading channels has been proposed.The amount of harvested energy at each relay is modeled as a finite Markov chain and then the approximate closed-form expression of the outage probability and ergodic sum-rate are derived.Simulations are carried out to verify the effectiveness of the theoretical analysis.It is concluded that through carefully choosing the system parameters of the network,(e.g.,EH threshold),FD-NOMA performs much better than the HD-NOMA or the conventional OMA.

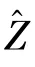
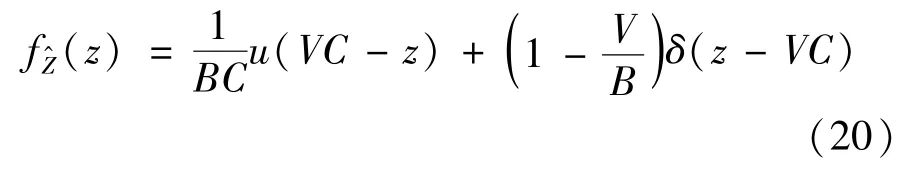
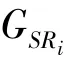
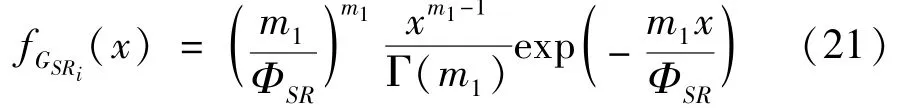
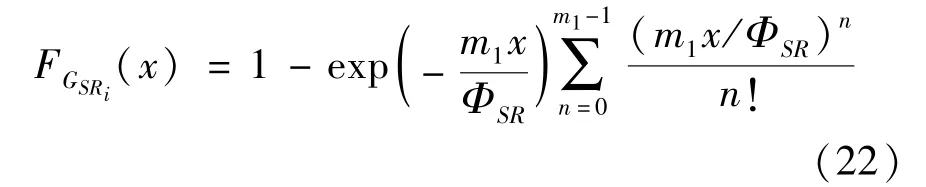
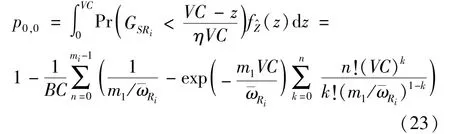

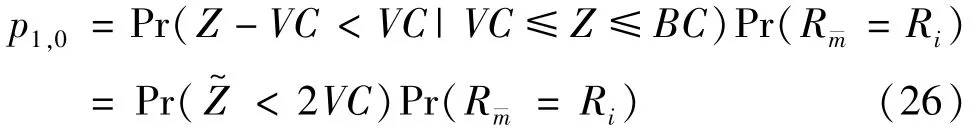
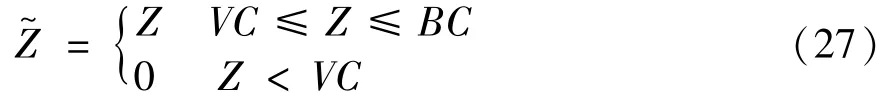
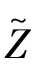
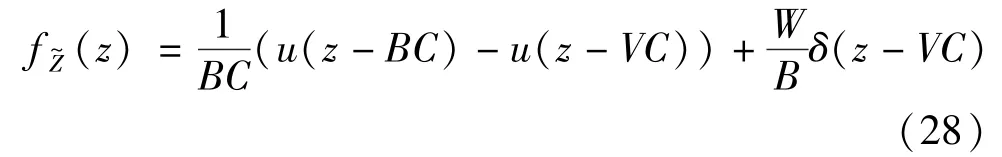

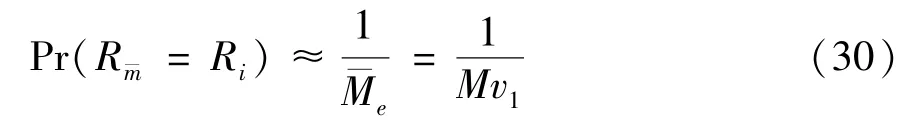
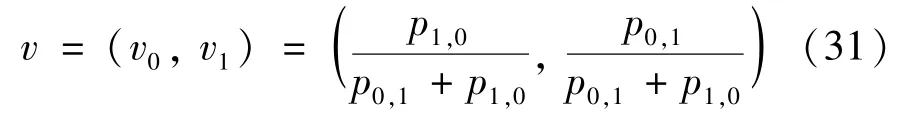
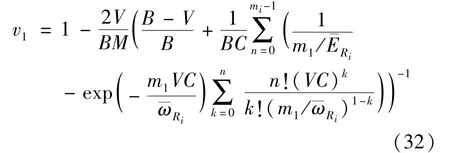
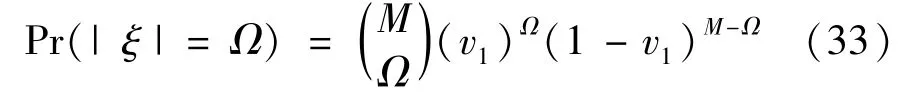
3 Performance analysis
3.1 Outage behavior
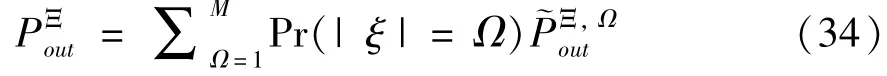
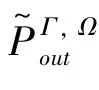
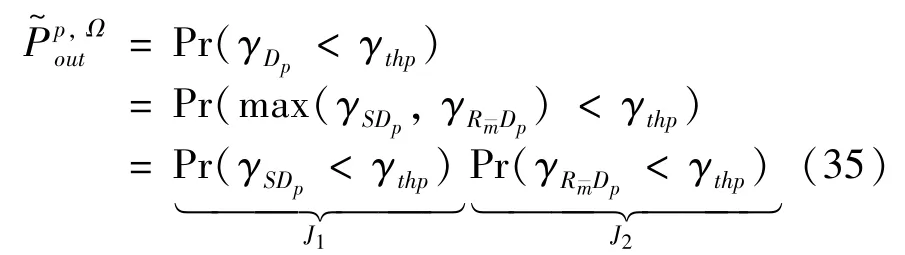
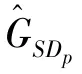
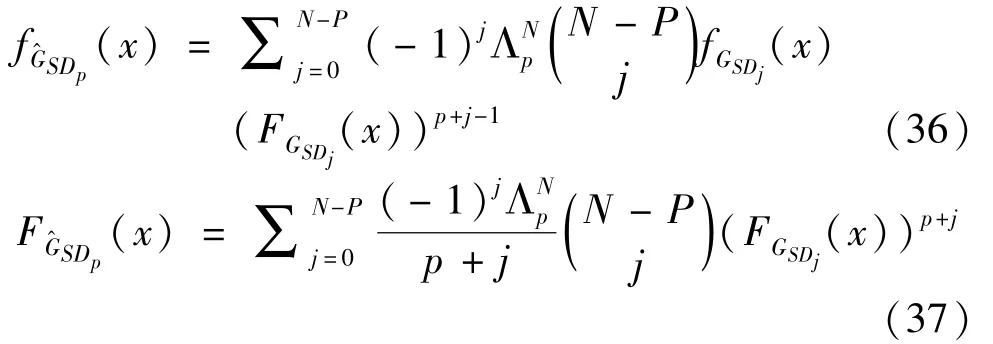
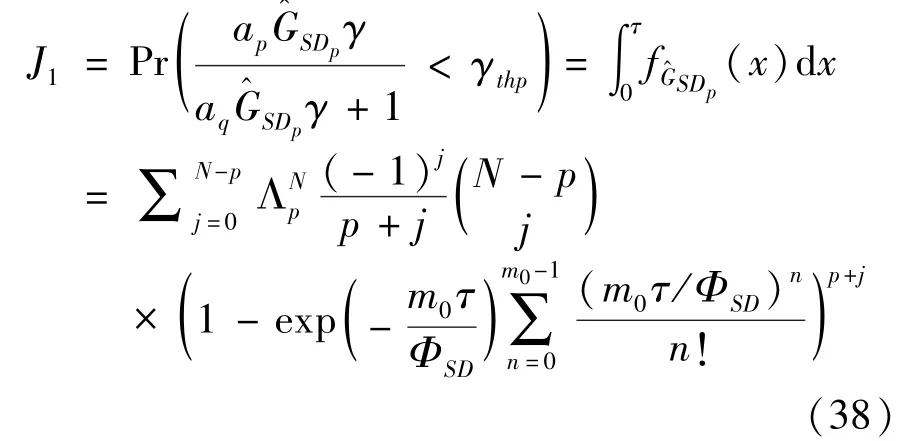
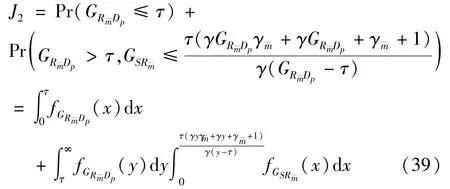
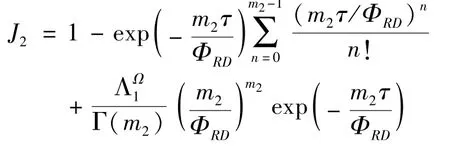
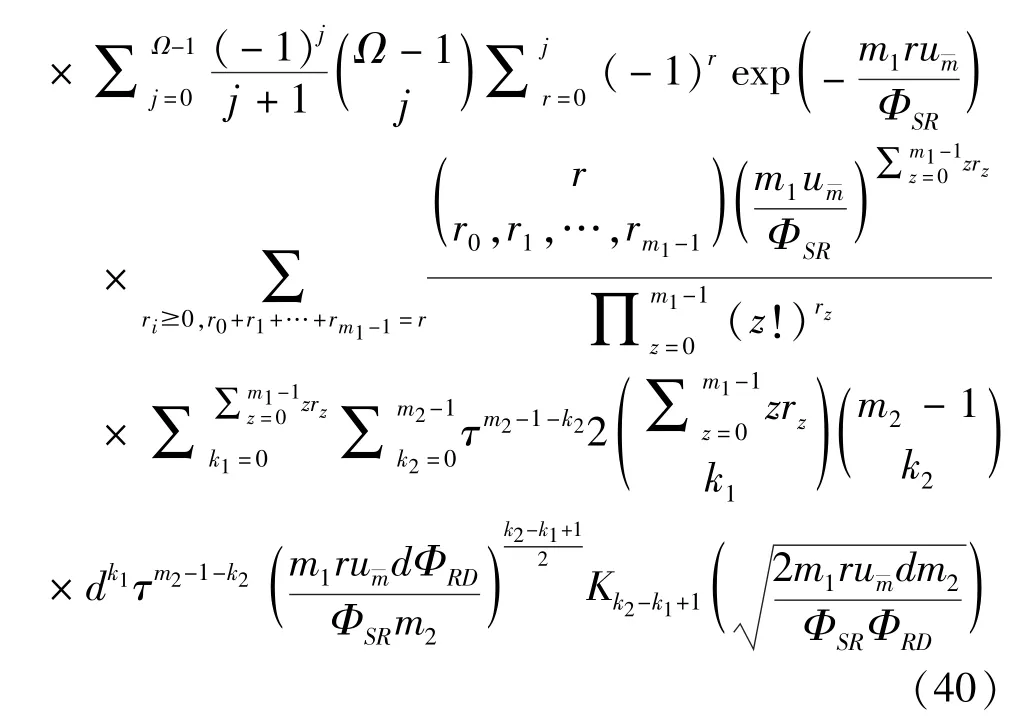
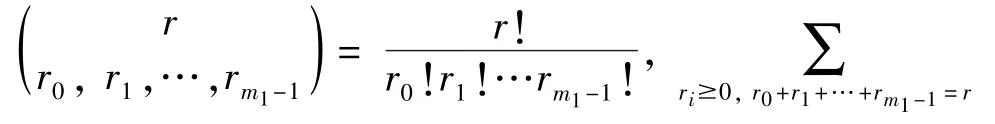
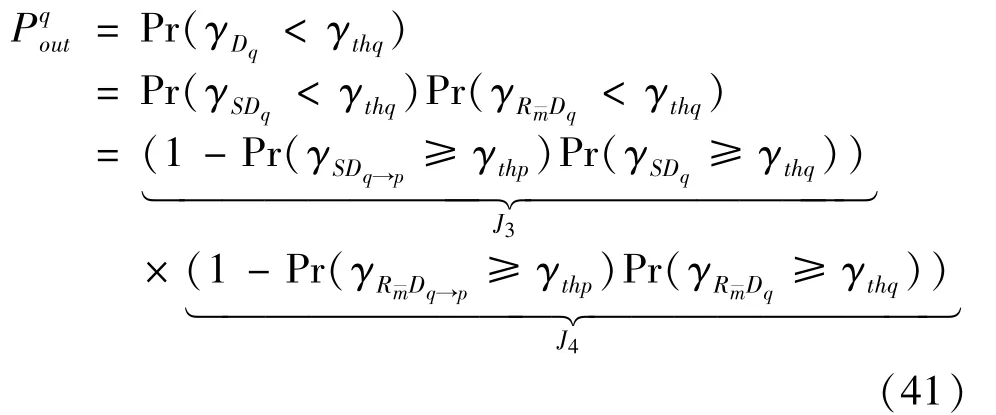
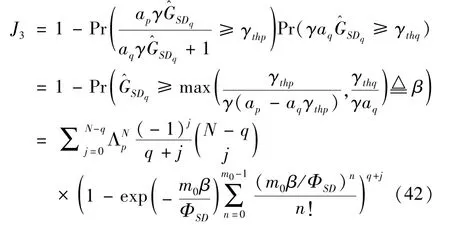
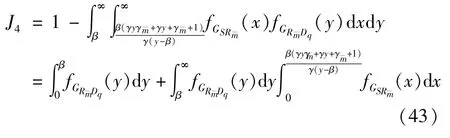
3.2 Ergodic sum-rate
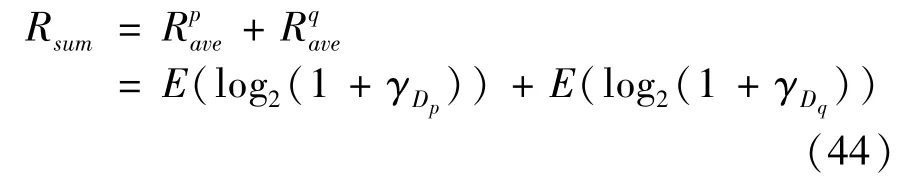

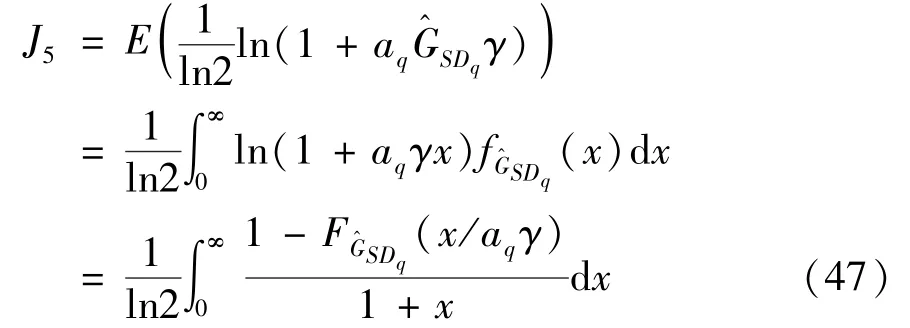


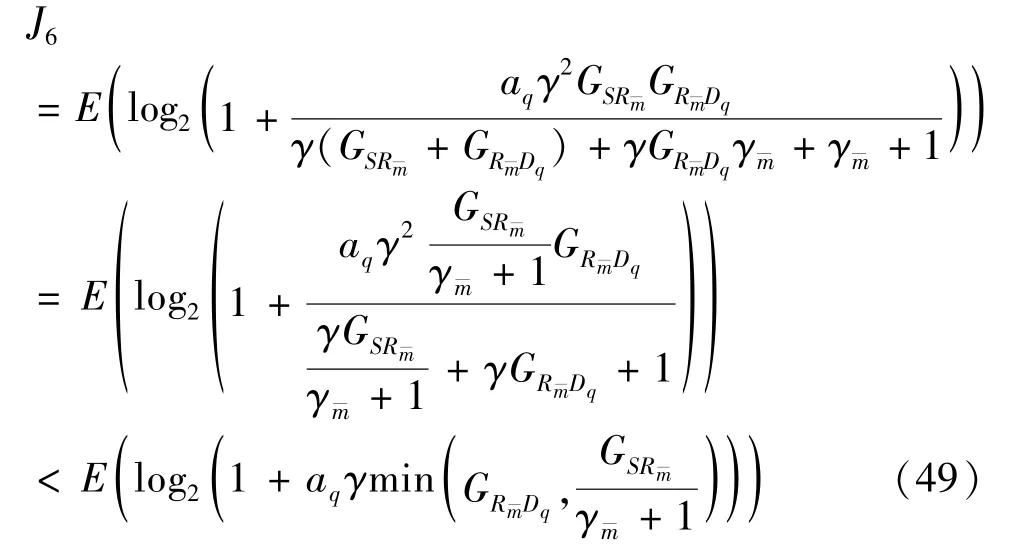
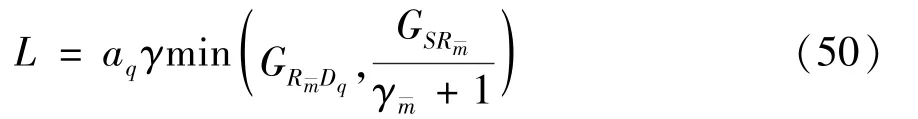
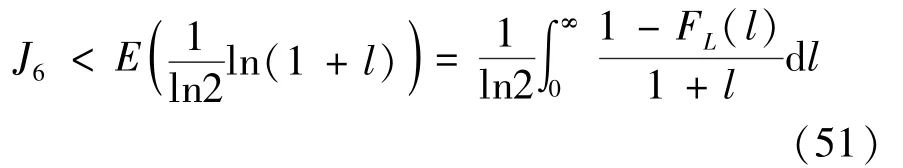
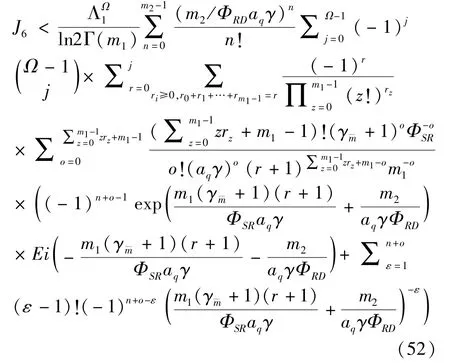
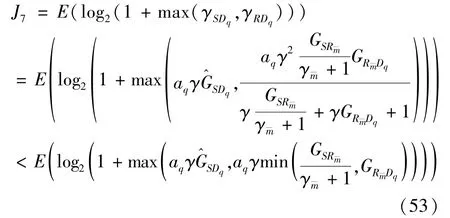
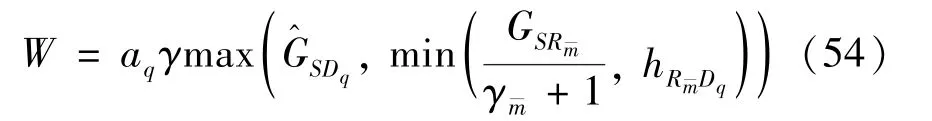
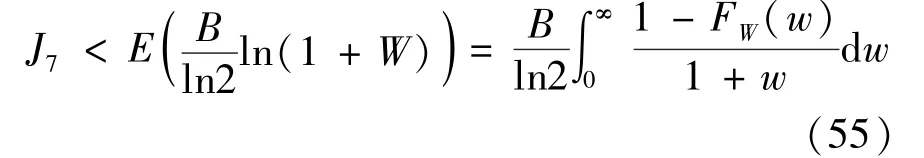
4 Results and discussion

5 Conclusions
 High Technology Letters2021年4期
High Technology Letters2021年4期
