Yu-Song Hu(胡玉松),Min Jiang(江敏),Tao Hong(洪濤),?,Zheng-Ming Tang(唐正明),and Ka-Ma Huang(黃卡瑪)

1School of Electronic Information Engineering,China West Normal University,Nanchong 637000,China

2College of Electronics and Information Engineering,Sichuan University,Chengdu 610065,China

Keywords:linear reaction,probability distribution,magnetization,anisotropic

1.Introduction

Microwaves,as one of the clean and highly effective energy,have been widely applied to chemical industry.In particular,the application of microwave energy to magnetic materials,e.g.,reduction of carbon bearing hematite fines and magnetite concentrate,[1]pig iron production,[2]reduction of magnetite iron coal composite particles,[3–5]was investigated,and the microwave reduction process is superior to conventional reduction in most cases.It is found that the magnetism of magnetite may be affected by microwave energy.For instance,the magnetic properties of NiMn2O4was controlled by the reduction reaction under the microwave magnetic field irradiation.[6]The influence of spin wave excited by microwave magnetic-field on magnetic material was investigated through the reaction kinetics of NiMn2O4under microwave magnetic-field heating.[7]However,thermal runaway and non-uniform heating may occur in the microwave heating process,since the relaxation of the magnetization in the reaction is barely investigated and most of the studies are only relevant to the chemical kinetics of magnetite in the microwave fields.

The magnetic relaxation of the magnetic particles has attracted much attention for a long time.Louis N′eel found that a particle of ferromagnetic material with a diameter of about 10 nm constitutes a single-domain particle showing strong thermal fluctuations.[8]Quasistatic magnetization curve of single-domain particles would be of Langevin type when the thermal energy is greater than or comparable to the anisotropy energy,especially at high temperatures.Thermal fluctuations of the magnetic particles should be taken into account to describe magnetic response of single-domain magnetic particles.A statistical approach was proposed to describe the magnetic response of single-domain magnetic particles by Brown.[9]Some researchers paid attention to the magnetic relaxation of anisotropic ferromagnetic particles under an external field,e.g.,the relaxation time of a single domain ferromagnetic particle under a collinear field,[10]and the magnetic relaxation of uniaxial single-domain ferromagnetic particles under a uniform magnetic field,[11]under an arbitrary strength AC magnetic field[12]or under a strong DC magnetic field of arbitrary orientation.[13]However,the magnetic relaxation of the reacting magnetic particles is barely studied.

In this paper,the response of the magnetization in uniaxial anisotropic single-domain magnetic particles with linear reaction dynamics is studied in a weak DC or AC magnetic field.The magnetization and the probability distribution of the magnetic particles in the reaction system are derived based on the reaction–diffusion theory.Then,the effect of the reaction process on the magnetization is discussed,and the results are compared with those from other models.

2.Basic equations

In the presence of a magnetic field,the dynamics of the magnetization of uniaxial single-domain magnetic particles can be described by Gilbert’s equation[14]

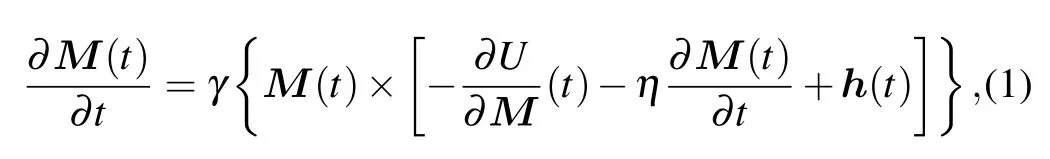
where h(t),U,γ,M(t),andηare the random field,the free energy per unit volume,the gyromagnetic ratio,the magnetization,and the damping parameter,respectively.

The parameter U in a time-harmonic field can be described as[13]

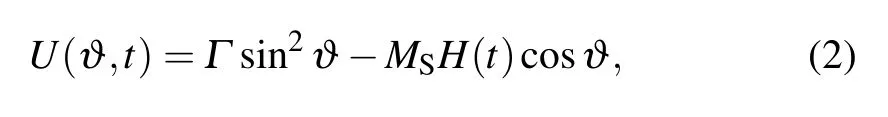
whereΓ,H(t),?,and MSrepresent the uniaxial anisotropy constant of the particle,the external field,the polar angle,and the saturation magnetization,respectively.Equation(1)can be expressed as the form of the Fokker–Planck equation(FPE)for the probability distribution function W of the orientation M[14]

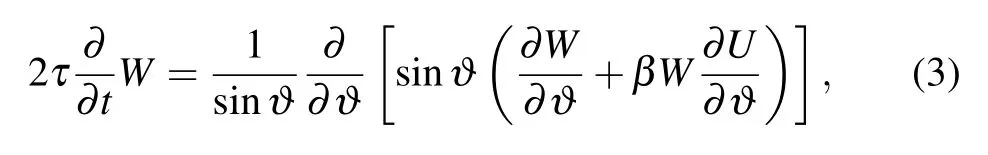
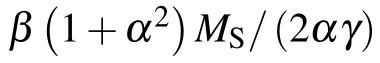
However,in an isomerization reaction with linear reaction dynamics,equation(3)is no longer suitable for describing the probability distribution function,and the chemical reaction process should be taken into consideration.[15]In this paper,the reactants decrease at a constant rate and the products are assumed to be nonmagnetic.Affected by the magnetic field,the magnetic reactants rotate with the external magnetic field,and split stochastically with reaction process proceeding simultaneously.Thus,the probability distribution function of the reactant concentration will depend on not only the rotational Brownian motion,but also the chemical process.Therefore,equation(3)for the probability distribution of the orientation will be modified with the rate of chemical reaction,which is similar to the scenario in Ref.[16],and the resulting equation is shown below:

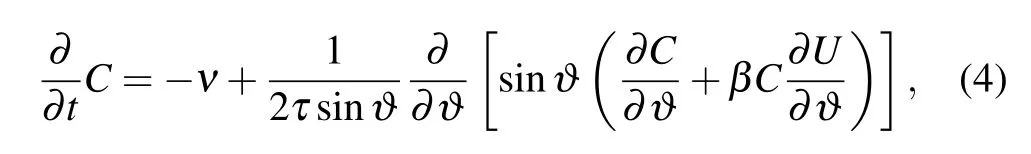
where C represents the probability distribution function of the reactant concentration,andνdescribes the effect of the reaction process,which is given by[15,17]

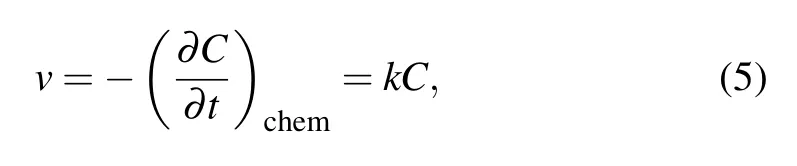
where k is the chemical reaction rate constant.

An infinite hierarchy of differential-recurrence equations for Eq.(4)can be obtained to simplify the derivation by using the Legendre polynomials Pn(cos?),

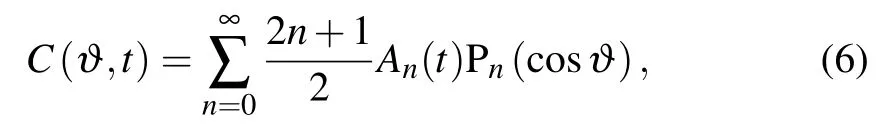
where An(t)is the corresponding coefficient of the Legendre polynomials.

Taking Eq.(6)into Eq.(4),we get

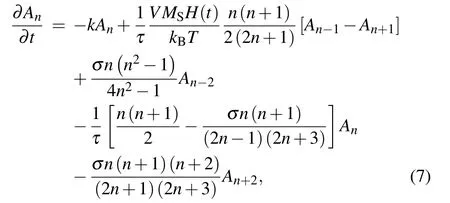
whereσ=βΓ.The high-order magnetic field is neglected to simply the calculation of magnetization M(t),since the external field is weak.By using the orthogonality of the Legendre polynomials,M(t)can be expressed as[18]

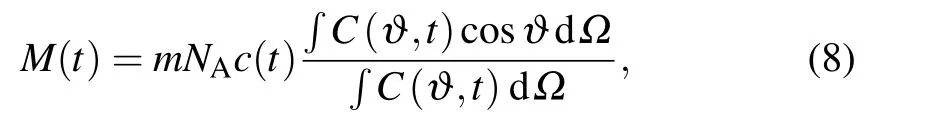
where NAis Avogadro’s number,

is the magnetic moment of a particle,and c(t)is the concentration.

In the irreversible isomerization reaction,only one reactant is considered here.Therefore,the magnetization can be obtained by combining Eqs.(6)and(8)

Because equation(7)is an infinite hierarchy of differentialrecurrence equations,it is very difficult to acquire its analytical solution.Now,by assuming that the energy of external field applied is weaker enough than the thermal energy,only the first two expansion coefficients need to be calculated to obtain the analytical expression in this situation.

Setting n=0,equation(7)will be changed into

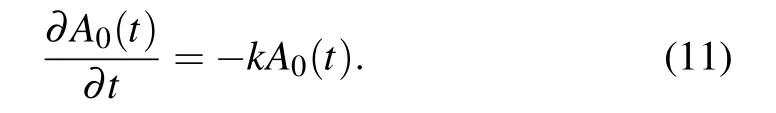
The form of Eq.(11)is similar to that of the linear reaction dynamic equation,so we can obtain the expression of A0(t)as follows:

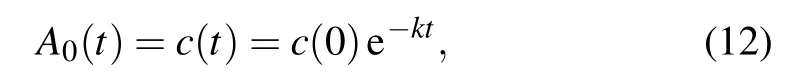
where c(0)is the initial concentration.

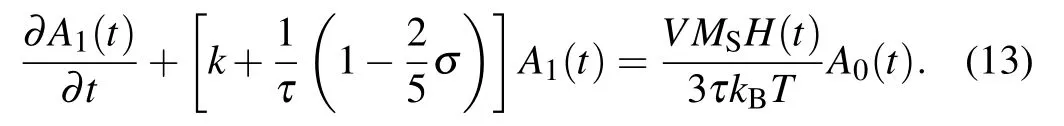
Setting n=1 and neglecting the higher-order magnetic field,equation(7)can be expressed as It can be seen that equation(13)is reduced to a constantcoefficient differential equation.We assume that the chemical reaction is started at t=0 and the external field is added at the same time.Therefore,we may regard the whole system as an equilibrium system for t<0.The analytic solution of Eq.(13)is obtained by the Laplace transformation

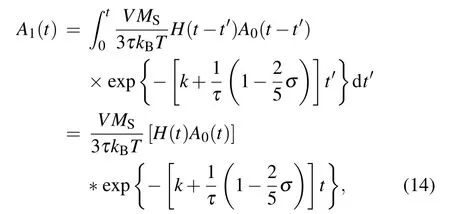
where?means the convolution.

Substituting A0(t)and A1(t)into Eqs.(6)and(10),we can obtain the expressions of the magnetization and the distribution function as follows:

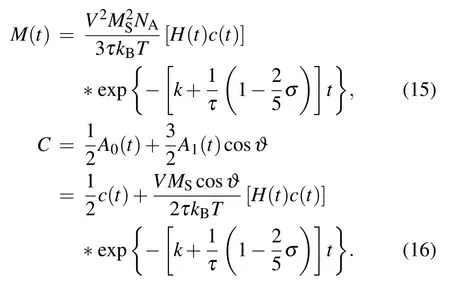
3.Results and discussion

3.1.Static or harmonic magnetic field

The expression of the magnetization is derived based on the Legendre polynomials as shown in Eq.(15).It can be seen that the magnitude will decrease with time increasing,because the reactant is gradually annihilated with the reaction.A similar phenomenon can be observed in Eq.(16).Equation(15)shows that the magnetization varies withσand can be affected by the external magnetic field and chemical reaction process.

For a weak DC field,equations(15)and(16)can be expressed by

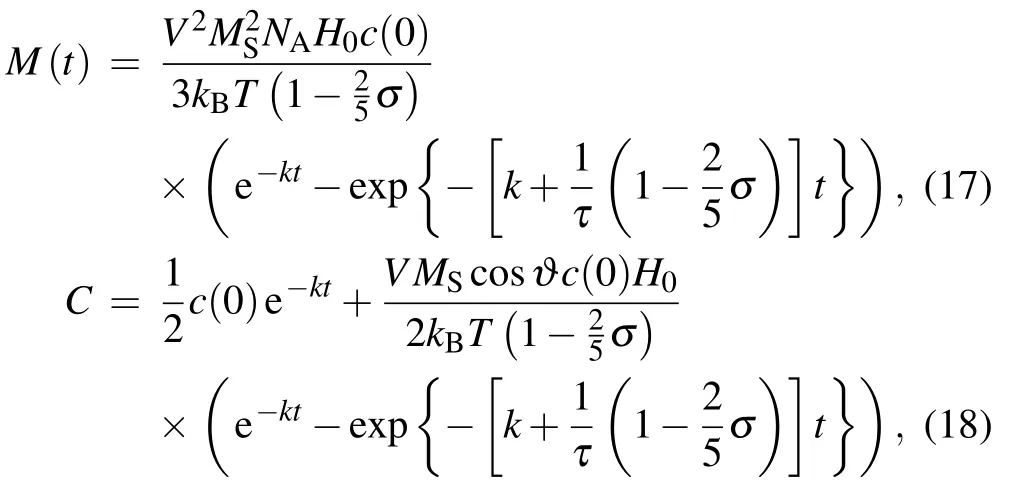
where H(t)=H0is the amplitude of the magnetic field.

For a weak AC field,H(t)=H0cosωt(ωis the angular frequency),equations(15)and(16)can be expressed by

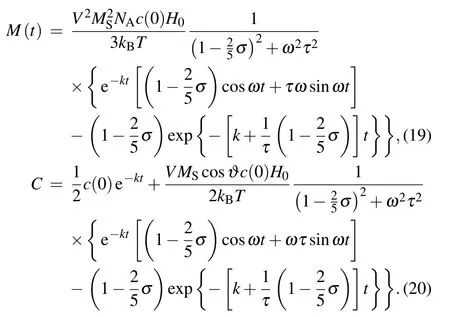
For uniaxial isotropic ferromagnetic particles(σ=0),we obtain

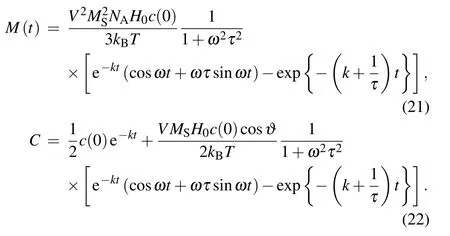
In order to intuitively understand the influence of anisotropy value,the numerical simulation is carried out.For a weak external field and slow chemical reaction,we assume ξ=VMSH0/kBT=0.5,k=0.1,andτ=0.5.The angular frequency of the time-harmonic field is set to be 1.Different values of the anisotropy parameter is taken into consideration.When the anisotropy parameter is positive or negative,the component in the vertical or horizontal direction plays a dominant role,which directly affects the instantaneous value of magnetization.

The concentration probability distribution functions of the magnetic particles at various times are shown in Fig.1,with the parameterξ=0.5,k=0.1,τ=0.5,σ=?2,?1,?0.5,0,0.5,1,2,andω=0 or 1.Hereω=0 or 1 represents the static magnetic field or the harmonic magnetic field,respectively.As shown in Fig.1,due to the reaction process,the mean value of the probability distribution function decreases with time increasing.At the same time,the case with smaller value ofσshows a more homogeneous distribution of the particles in the dc magnetic field.Affected by the harmonic magnetic field,the trend of the mean value of probability distribution function is uncertain,and the case with smallerσpresents a more homogeneous distribution.

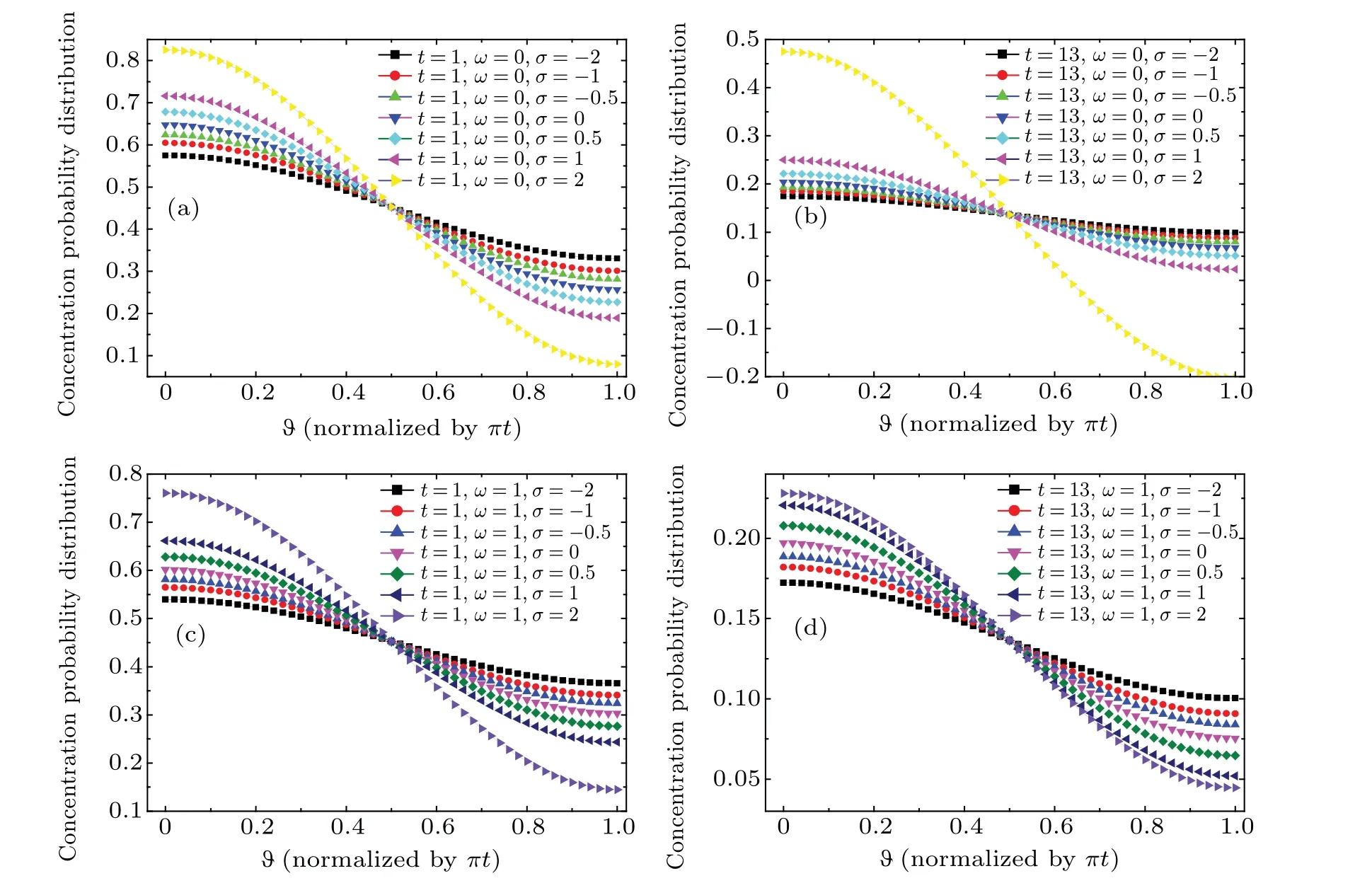
Fig.1.Concentration probability distributions(normalized by c(0))of magnetic particles in reaction system with(a)ω=0,t=1;(b)ω=0,t=13;(c)ω=1,t=1;and(d)ω=1,t=13,forσ=?2,?1,?0.5,0,0.5,1,2.

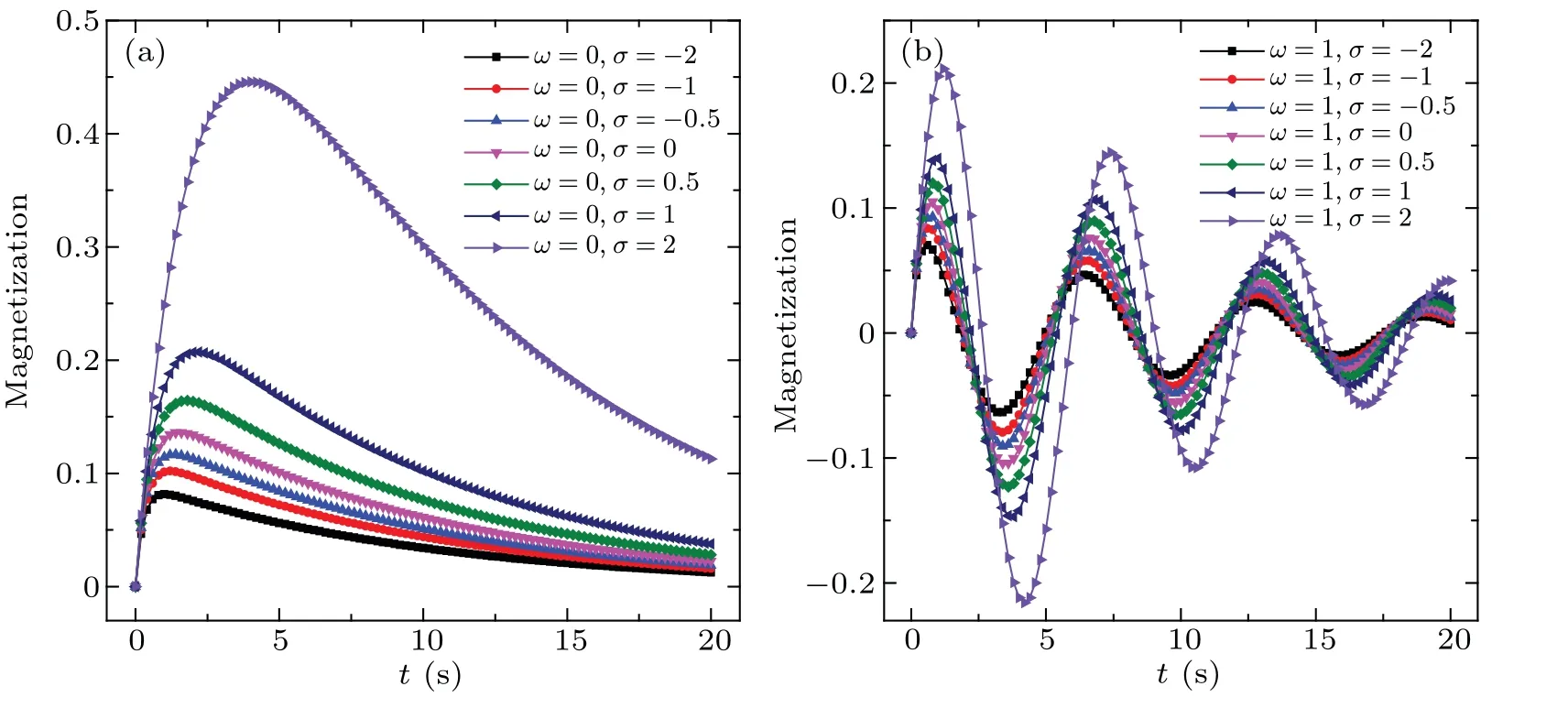
Fig.2.Magnetization(normalized by NAMSVc(0))of the reaction magnetic particle system with(a)ω=0 and(b)ω=1 in time range from 0 s to 20 s,forσ=?2,?1,?0.5,0,0.5,1,2.

In Fig.2,the magnetization of the reacting magnetic particles is shown withξ=0.5,σ=?2,?1,?0.5,0,0.5,1,2,k=0.1,τ=0.5 andω=0 or 1.The results show that the magnetization reaches a maximum value quickly then decreases with time increasing in the DC field case,for which the reason is similar to that for the probability distribution function in Fig.1.In the ac magnetic field case,the amplitude of the magnetization varies with the external magnetic field frequency,which is similar to the process of the damped oscillation.The case with larger value ofσshows a higher peak of magnetization in the DC magnetic field,and also in the AC magnetic field.

3.2.Comparison with other models

In order to compare with the reaction-free case,the magnetization function and the probability distribution function of the reaction-free magnetic particle system are derived.Let c(t)equal the initial concentration,then we will obtain the following equations:

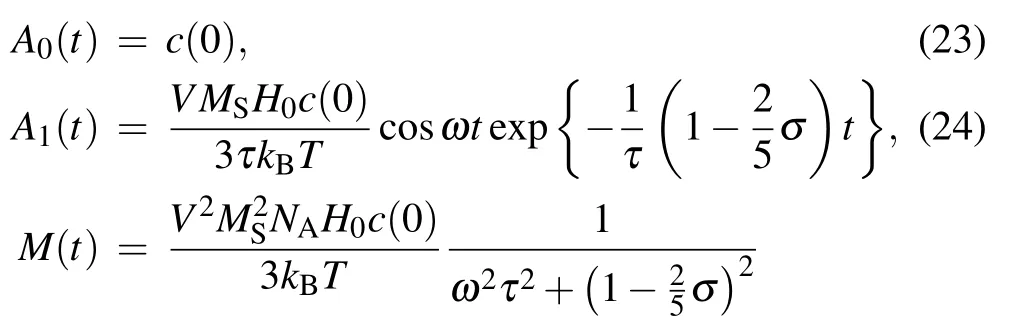
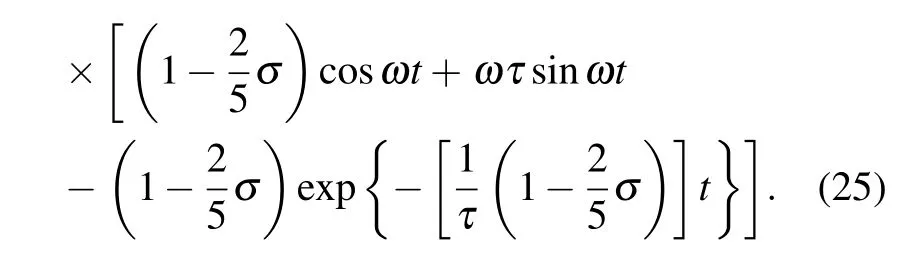
In Fig.3,the magnetization of the magnetic particles with or without reaction process is shown withξ=0.5,σ=2,k=0.1,τ=0.5,andω=1.In the non-reaction case,the magnetization reaches a maximum valie and keeps dynamic balance after one magnetic field period,since none of the magnetic particles can timely response to the external field when the relaxation time is close to the period of the field applied.In the reaction case,the magnetization decreases with time increasing.A conclusion can be made that the influence of the chemical reaction on the magnetization cannot be ignored because the reactants change with the process of reaction.

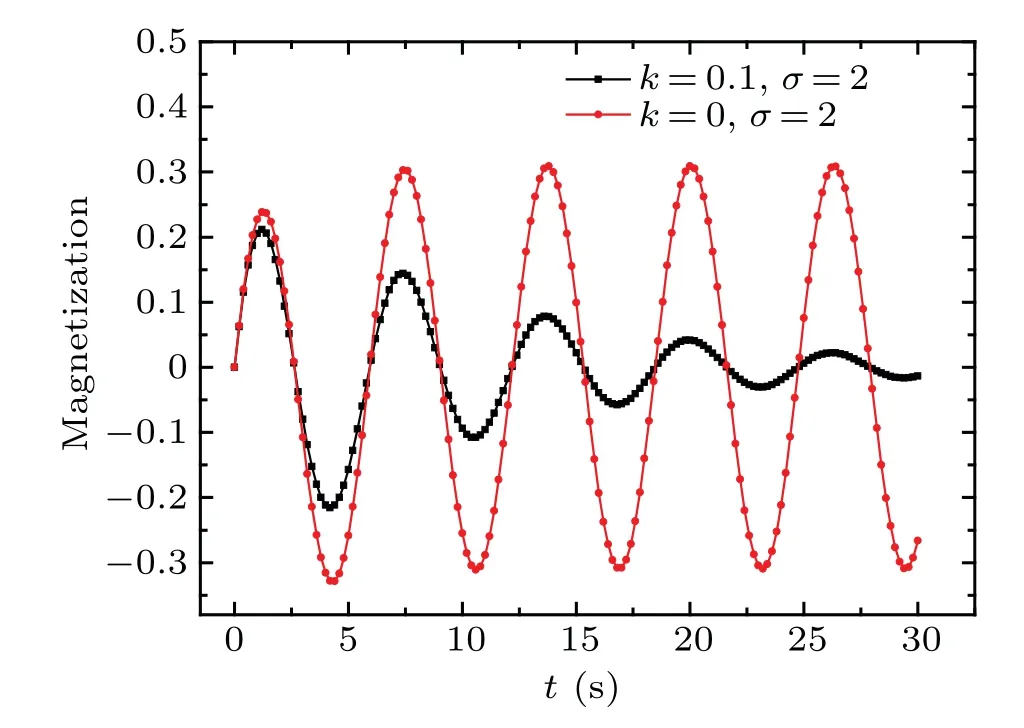
Fig.3.Comparison between the curves of magnetization(normalized by NAMSVc(0))versus t of the particles with or without reaction.

On the other hand,if the anisotropic parameter is ignored,equation(21)is similar to the result of Ref.[16]in the isomerization reaction case.Moreover,when the reaction dynamics is also ignored,equation(25)is similar to the expression in Ref.[19]in the weak external field.Once both the reaction dynamics and the anisotropic parameter are ignored,forσ=0 and k=0,the results can be reduced to

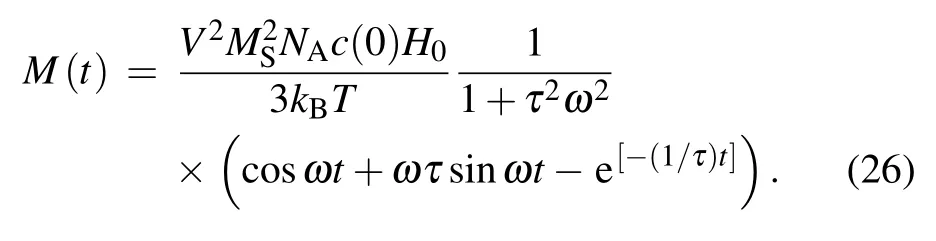
Equation(26)is similar to the expression of Debye mode in an external time-harmonic field indicated in Ref.[20].Their only difference lies in the exponent term in Eq.(27),if the lower limit of integral is assumed to be negatively infinite,equation(28)turns into an equation whose form is the same as the Debye mode’s.

4.Conclusions

We have derived the magnetization and the concentration probability distribution of uniaxial anisotropic single-domain ferromagnetic particles with linear reaction dynamics subjected to AC or DC bias magnetic field based on the reaction–diffusion equation theory.By using the Legendre polynomials,we obtain the expression of magnetization and distribution function.As the reactants vanish with time increasing,both magnetization and distribution function decrease with the chemical process.On the other hand,the external magnetic field has an obvious influence on the properties of magnetic reactants.The uniformity of the probability distribution is affected by the anisotropic parameter.The case with smaller anisotropic value shows a more homogeneous distribution of the particles.The trend of the magnetization is different from the that of the concentration probability distribution,and the amplitude of magnetization shows higher peak in DC magnetic field and also in the AC magnetic field when the anisotropic value is larger.The magnetization reaches a maximum value and keeps dynamic balance after one magnetic field period in the non-reaction case.The magnetization decreases with time increasing due to the reaction process in the reaction case.Meanwhile,the magnetization of the chemical reaction can be reduced to the expressions of different modes when the anisotropy or the reaction process,or both of them are ignored.