Wen-Xiu Ma

Department of Mathematics,Zhejiang Normal University,Jinhua 321004,Zhejiang,China

Department of Mathematics,King Abdulaziz University,Jeddah 21589,Saudi Arabia

Department of Mathematics and Statistics,University of South Florida,Tampa,FL 33620-5700,United States of America

School of Mathematical and Statistical Sciences,North-West University,Mafikeng Campus,Private Bag X2046,Mmabatho 2735,South Africa

Abstract A linear superposition is studied for Wronskian rational solutions to the KdV equation,which include rogue wave solutions.It is proved that it is equivalent to a polynomial identity that an arbitrary linear combination of two Wronskian polynomial solutions with a difference two between the Wronskian orders is again a solution to the bilinear KdV equation.It is also conjectured that there is no other rational solutions among general linear superpositions of Wronskian rational solutions.

Keywords:soliton equation,Wronskian solution,rational solution,rogue wave,the KdV equation

1.Introduction

The Wronskian formulation is one of powerful approaches to soliton solutions[1,2].It has been generalized to present more diverse solutions[3,4],particularly rational solutions and complexiton solutions[5,6].There are plenty of recent studies on nonlinear dispersive waves[7–9],including optical solitons and rogue waves[10–12].The corresponding soliton equations and even hierarchies of soliton equations can be solved through the inverse scattering transform[13–15]and Riemann–Hilbert problems(see,e.g.[16]).

It is shown[5]that when the functionsφi,0≤i≤N-1,satisfy

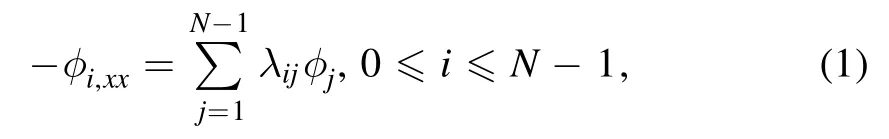
and

whereλijare arbitrary constants,the Wronskianf=W(φ0,φ1,…,φN-1)yields a solutionu=-2 (lnf)xxto the KdV equation

Particularly,rational,soliton,negaton and complexiton solutions correspond to the cases of zero,positive,negative and complex eigenvalues of the coeffciient matrixΛ=(λij)0≤i,j≤N-1,respectively[5].

One of the resulting rational solutions is given byassociated withφ0=x.Through the x-translational and ttranslational invariance:=u(x+a,t+b)and the Galilean invariance:=u(x+6ct,t)+c,where a,b and c are arbitrary constants,we can generate rogue wave solutions from the Wronskian rational solutions for the KdV equation.Obviously,one such rogue wave solution is

wherea≠0,b and c are arbitrary real constants,and a special case withb=0 andc=-1 leads to the rogue wave solution presented recently in[17]:

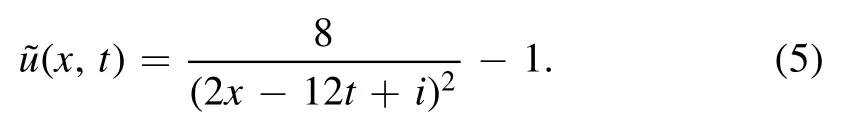
Generally,since the KdV equation is nonlinear,the linear superposition principle can not be applied to its solutions.However,a special linear superposition can exist among Wronskian rational solutions to the KdV equation.This will be the main topic of our discussion in this paper.More specifically,we would like to explore a linear superposition principle for two Wronskian rational solutions to the KdV equation,which have a difference two between the orders of the two involved Wronskian determinants.

The rest of the paper is organized as follows.In section 2,we will set up Wronskian rational solutions.In section 3,we will present a polynomial identity,originated from a linear superposition of Wronskian rational solutions,and in section 4,we will show that it is equivalent to the polynomial identity that a sum of two Wronskian polynomial solutions with a difference two between the Wronskian orders is again a solution to the bilinear KdV equation.A few concluding remarks will be given in the final section,together with a conjecture on general linear superpositions of Wronskian rational solutions.

2.Wronskian rational solutions

Let us recall that the KdV equation(3)is transformed into a Hirota bilinear form

underu=-2 (lnf)xx[5].Actually,we have

Obviously,a polynomial solution f to the bilinear KdV equation(6)will lead to a rational solution to the KdV equation(3)by the indicated transformation.

LetN≥0 be an arbitrary integer.Assume that fNis a polynomial solution,defined by the Wronskian[5]:

whereφi,i≥0,are polynomial functions of x and t,determined by(1)and(2)with

We only consider the above case of the coefficient matrix Λ,since similar transformations of Λ generate the same Wronskian solutions to the KdV equation.

Some examples of such Wronskian rational solutions are determined by[5]:

More examples can be generated from the Adler–Moser polynomials introduced in[19].The Wronskian rational solutions can also yield rogue wave solutions through using the x-translational and t-translational invariance and the Galilean invariance of the KdV equation,as illustrated earlier.

3.A polynomial identity

For a sequence of smooth functions of x:φi=φi(x),i≥0,we define

Assume thatm,n≥1 are two integers.Note that a Wronskian of order m is denoted by

Similarly,let us denote

We will discuss about Wronskian rational solutions,and so let us focus on the sequence of polynomialsφi,i≥0,determined by

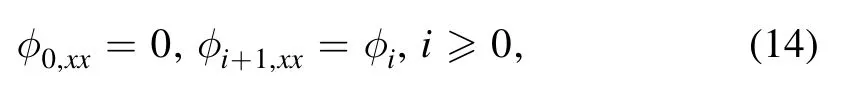
which follows from the assumption for Λ in(9).

A polynomial identity:LetN≥3 be an arbitrary integer.Then we conjecture[18]that under(14),the following equality holds for generalized Wronskians:

More compactly,the identity(15)can be expressed as

or rewritten in an even more compact form:

By the Laplace expansion around the firstN+2 rows,we can also put(15)simply in a determinant form:

It can be readily seen thatf1+f3andf2+f4solve the bilinear KdV equation(3),where fm's are the Wronskian solutions defined by(8).In the general case,we would like to show that the identity in(15)is equivalent to say thatfN+fN+2is again a polynomial solution to the bilinear KdV equation(6).We refer the reader to[19,20]for more illustrative examples of such solutions generated from linear combinations.without any sign change in the six terms,where

and

The identity(15)is very similar to the simplest case of the Plücker relations[7],but we do not know what kind of mathematical property it reflects really.It might be helpful in proving the identity(15)if we apply the Laplace expansion for determinants and Jacobi’s identity for Wronskians:

The identity(15)will be used to show a linear superposition principle for Wronskian rational solutions,including rogue wave solutions,to the KdV equation.

4.Linear superposition

It is common sense that there is no linear superposition principle for nonlinear equations.However,among the Wronskian rational solutions to the KdV equation,we would like to explore a special kind of linear superpositions of solutions.

Let f and g be two Wronskian solutions to the bilinear KdV equation(6).Then,we have

where c is an arbitrary constant.Therefore,for two Wronskian solutions f and g,we see that an arbitrary linear combination of f and g solves(6)iff so does f+g.

Theorem 4.1.LetN≥3 be an arbitrary integer and the polynomial functionsφi,i≥0,determined by(14)and

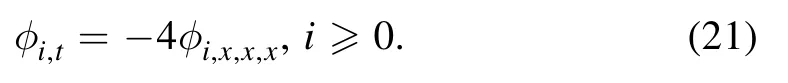
Then for the bilinear KdV equation(6),fN+fN+2=a sum of two Wronskian solutions,again presents a solution iff the equality(15)holds.Proof:Note thatλii=0,i≥0.By(2.5)of lemma 2.2 in[5],we have

and computing its derivative with respect to x leads to

By(2.7)of lemma 2.2 in[5],we have

and combining(2.7)and(2.8)of lemma 2.2 in[5]tells

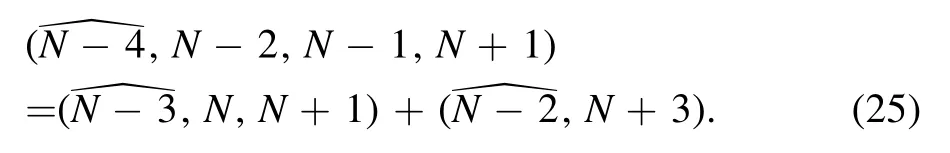
where we have used(22)and(25)in(27)and(29),respectively.Moreover,by using the conditions in(21),we have

and then,upon using(23)and(24)in(30)and(31),respectively,we obtain

Now,it is direct to see that

and

5.Concluding remarks

We have discussed about a specific linear superposition of Wronskian rational solutions to the KdV equation.It has been explored that it is equivalent to a polynomial identity that a linear combination of two Wronskian polynomial solutions with a difference two between the Wronskian orders is again a solution to the bilinear KdV equation.

It is easy to see that there is only the linear combination solution

among

where fmis the Wronskian of order m defined by(8)andci,1≤i≤5,are arbitrary constants.We conjecture that such a statement in a general case will be true,i.e.there is no other solution among the linear combinations

wheren≥1 is an arbitrary integer andci,1≤i≤n,are arbitrary constants,besidesfN+c2fN+2.

Recently,there have been various studies on a kind of simple but important rational solutions,called lump solutions,to nonlinear dispersive wave equations(see,e.g.[21,22])and different nonlinearities can go together to engender nonlinearity-managed lump solutions[23,24].It is known that for local integrable equations,soliton solutions can be derived from the τ-function[25]and Hirota bilinear forms(see,e.g.[26]),and lump solutions can be obtained by taking longwave limits of soliton solutions[27].How about generating lump solutions for nonlocal integrable equations?Can we apply the Riemann–Hilbert technique(see,e.g.[28,29]for solitons)to exploring their phase interaction characteristics?Certainly,any investigation in this research area would be helpful in understanding complex dynamical phenomena(see,e.g.[30,31])in dispersive wave theories.

Acknowledgments

The work was supported in part by NSFC under the Grant Nos.11975145 and 11972291.The authors would also like to thank Alle Adjiri,Ahmed Ahmed,Mohamed Reda Ali,Yushan Bai,Nadia Cheemaa,Morgan McAnally,Solomon Manukure,Rahma Sadat Moussa,Fudong Wang and Melike Kaplan Yal??n for their valuable discussions.