Ammarah Raees,Umer Farooq,Muzamil Hussain,5,Waseem Asghar Khanand Fozia Bashir Farooq

1 Faculty of Computer Science and Software Engineering,Huaiyin Institute of Technology,Huai’an,China

2 Department of Mathematics,COMSATS University Islamabad,Park Road Chak Shahzad Islamabad 44000,Pakistan

3 Department of Mathematics,College of Sciences AlZulfi,Majmaah University,Al Majma’ah,11952 Saudi Arabia

4 Department of Mathematics,Imam Muhammad ibn Saud Islamic University,Riyadh 11432,Saudi Arabia

5 Department of Mathematics,University of the Poonch Rawalakot,Rawalakot 12350,Pakistan

Abstract The aspiration of this research is to explore the impact of non-similar modeling for mixed convection in magnetized second-grade nanofluid flow.The flow is initiated by the stretching of a sheet at an exponential rate in the upward vertical direction.The buoyancy effects in terms of temperature and concentration differences are inserted in the x-momentum equation.The aspects of heat and mass transfer are studied using dimensionless thermophoresis,Schmidt and Brownian motion parameters.The governing coupled partial differential system(PDEs)is remodeled into coupled non-similar nonlinear PDEs by introducing non-similar transformations.The numerical analysis for the dimensionless non-similar partial differential system is performed using a local non-similarity method via bvp4c.Finally,the quantitative effects of emerging dimensionless quantities on the nondimensional velocity,temperature and mass concentration in the boundary layer are conferred graphically,and inferences are drawn that important quantities of interest are substantially affected by these parameters.It is concluded that non-similar modeling,in contrast to similar models,is more general and more accurate in convection studies in the presence of buoyancy effects for second-grade non-Newtonian fluids.

Keywords:non-similar modeling,second-grade fluid,exponentially stretching surface,local non-similarity,bvp4c

1.Introduction

Study of the flows induced by the stretching of the surfaces is of significant importance in view of its use in technical manufacturing,such as aerodynamics,the cooling process of metal sheets,extrusion of plastic sheets,the condensation process of fluid films,chemical processing equipment,glass and polymer industries,crystal growth and several heat exchanger projects.In such situations,the outputs with the required attributes depend on the rate of cooling and stretching in the process.Sakiadis[1]was the pioneer in this field who theoretically explored the moving solid structures.He addressed the problem by applying similarity transformation via a numerical technique.Moreover,Erickson et al[2]continued the exploration by assuming a moving surface with nonzero transverse velocity.The 2D steady flow was investigated by Crane[3]over a stretching surface.He attempted to concentrate on a stretching sheet as he realized that this case was a pivotal subject in the polymer industry.Gupta and Gupta[4]utilized that that was introduced by Crane[3]and extended those examinations.They explored heat and mass transfer by incorporating suction effects over an expanding surface.Rajagopal et al[5]inspected the flow of viscoelastic fluid in the absence of heat transfer and discussed its applications in the polymer industry.Using the momentum integral method,Bujurke et al[6]performed convection studies for second-grade fluid flow.Magyari and Keller[7]examined steady flow using both analytical and numerical solutions.They also compared heat and mass transfer features of the considered problem with already proven results of earlier authors.Elbashbeshy[8]introduced a new dimension in the analysis of an exponentially stretching surface.He examined the effects of suction in a surface which is expanding at exponential rate.Partha et al[9]studied mixed convection flow with viscous dissipation consequences over a vertical surface expanding at exponential rate.Khan et al[10]studied viscoelastic fluid over an exponentially expanding surface.Xu et al[11]analytically examined the unsteady electrically conductive incompressible viscous fluid in which flow is initiated by the expansion of the surface in two lateral directions.Latterly Khan[12]and Bataller[13]analytically reviewed convection equations for viscoelastic fluid flow persuaded by a stretchable sheet.Tan and Liao[14]analytically examined the 3D unsteady incompressible viscous rotating fluid flow over an impulsive surface.Sajid and Hayat[15]surveyed thermal radiation effects in an exponentially expanding sheet.Sekhar and Chethan[16]examined heat transfer using Boussinesq–Stokes suspension numerically in the fluid flow,which is started by the exponentially expanding surface.Siddheshwar et al[17]expanded this research by considering the magnetic field in a transversal direction.Ramzan et al[18],with the help of surface heat flux,examined the effects of thermal radiation and mixed convection on 3D second-grade nanofluid.Rasheed and Anwar[19]studied magnetohydrodynamic(MHD)viscoelastic fluid flow with homogeneous–heterogeneous reactions in the flow domain.By utilizing the time-dependent magnetic field,Muhammad[20]analyzed the impact of heat absorption/generation effects over a curved surface.Ahmad et al[21]inspected 3D unsteady flow with thermophoresis and Brownian motion effects.Jamil et al[22]examined heat transfer of viscoelastic incompressible unsteady flow generated by a stretching surface with heat radiation and chemical reaction effects.Irfan et al[23]examined 3D MHD nonlinear radiated flow of mixed convection Carreau nanofluid over a stretching surface.

In accordance with industrial and technical applications,flow models based on non-Newtonian fluids are more acceptable than Newtonian fluids.Non-Newtonian fluids show a nonlinear stress and strain rate relationship at any point of flow.Mathematically,compared to the Newtonian the constitutive equations of non-Newtonian fluids are much more complex because of the nonlinear relation of the stress and strain rate.Constitutive equations are more complex,containing a number of parameters,and the solutions of the resulting equations are more complicated to find in general.Numerous variable viscous fluid models have been suggested which demonstrate the complexity of their governing equations.Now,several researchers are engaged in the study of analytical or numerical solutions to fluid flow problems that generate from the use of various non-Newtonian fluid models.Viscoelastic fluids are common types of non-Newtonian fluids.However,the most widely used basic type of viscoelastic fluid is the second-order fluid,which may address problems that are far from trivial.The fluid property viscoelasticity refers to the rise in the order of differential equations that describe the flow.Nevertheless,flow equations are typically more nonlinear compared to Newtonian fluid equations.Among these reasons,the field of research on non-Newtonian fluids poses some fascinating and impressive tasks for computer scientists,physicists and mathematicians alike.

Mathematical simulations of physical processes in fields such as fluid dynamics,diffusion,wave dynamics,chemical kinetics and general transport problems are governed by nonlinear partial differential equations whose solutions are difficult to find analytically.Consequently,the conversion technique for analyzing nonlinear partial differential system(PDEs)into ordinary differential equations(ODEs)has been very influential in the study of various convection equations.Ames[24]presented many types of these reduction approaches and thought about the developments in fluid dynamics,wave propagation and nonlinear diffusion from the use of PDEs to the reduction approach to ODEs.Although a similar approach has frequently been used in the literature[25–29],the approach cannot be used to a significant extent because of a limitation clarified underneath.Success of this approach depends vigorously on the achievement of a reduced ODEs solution.For a few cases,the reduced ODEs may be integrated in the form of elementary functions,but it is not an easy matter in most cases,so it was proposed that numerical methods be used to solve the converted ODEs.Generally,the given system is not fully converted to ODEs using a local similar method;to overcome this drawback Sparrow and Yu[30]introduced a method of local non-similarity.Hayat et al[31]numerically examined magnetic viscous fluid in nonlinear curved expansion.Zhang et al[32]investigated 3D pressure drop through a spherically coordinated helically coiled tube.Ray et al[33]utilized local non-similarity via a homotopy analysis scheme for mixed convection in the vertical flow of Eyring–Powell fluid with variable velocity.Farooq et al[34]employed local non-similarity via bvp4c for Darcy–Forchheimer–Brinkman flow in non-Darcy porous media.

The purpose of this work is to provide a realistic means of dealing with these circumstances in which governing equations cannot be reduced into ordinary differential systems.The laminar incompressible flow of magnetic secondgrade fluid over an exponentially expanding surface in the presence of buoyancy forces in terms of temperature and concentration with surface heat flux is considered.Under these premises,the governing convection differential equations are formulated.The appropriate non-similarity transformations are proposed.The governing equations are reduced into a dimensionless nonlinear partial differential system.The transformed system is solved numerically using local non-similarity via bvp4c,which is valid for a system of PDEs.Finally,tabular representations regarding the impact of concerning parameters on the friction coefficientCf,Nusselt numberNu,and Sherwood numberShare disclosed,and demonstrated graphically the effects of involved dimensionless parameters on the non-dimensional velocity,temperature and mass concentration profiles.

2.Formulation of convection equations

Consider mixed convection in a second-grade laminar,incompressible,steady,2D,magnetized second-grade fluid flow over a sheet positioned along thex-axis in the vertical direction,although fluid in the domainy>0 is constrained.It is also presumed that the sheet is stretched at an exponential ratewhereU0is the reference velocity.Figure 1 demonstrates the geometrical configuration of the present flow.

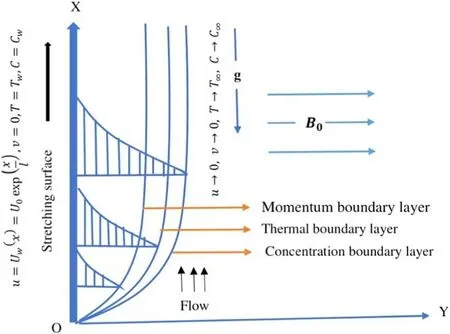
Figure 1.Flow over a hot vertical plate at temperature Tw immersed in a fluid at temperature∞T.

Figure 2.f′(η)for several values of“M”.

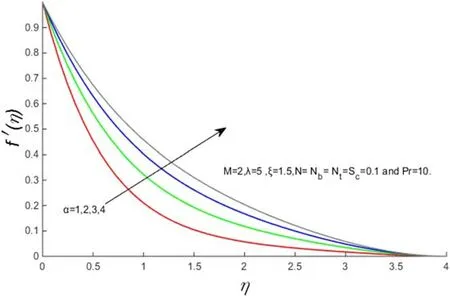
Figure 3.f′(η)for several values of‘α’.

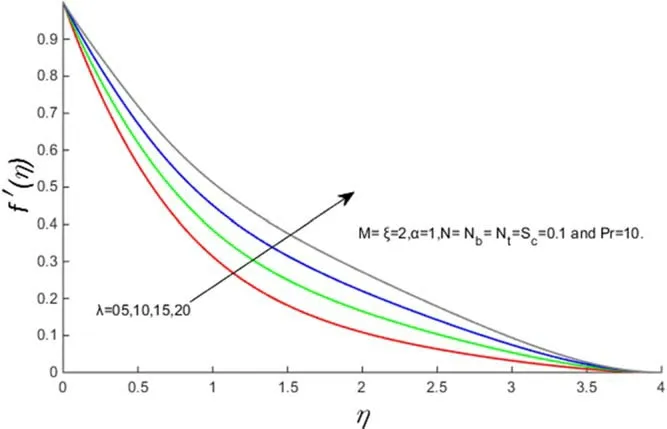
Figure 4.f′(η)for several values of‘λ’.

Figure 5.f′(η)for several values of‘N’.

The governing equations for

are as follows:

continuity equation

equation of motion

energy equation

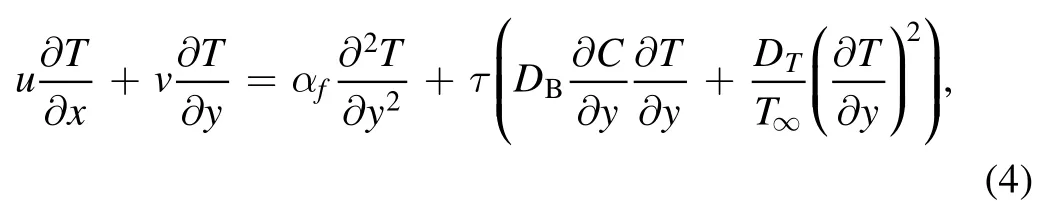
nanoparticle volume fraction equation

In the governing systemuandvare the velocity components along thex-andy-directions,whileTandCrepresent temperature and concentration variables,respectively,ρfis the fluid density,σrepresents the electrical conductivity,?is the kinematic viscosity,B0indicates the applied magnetic field,α1is the second-grade fluid material parameter,gis the gravitational acceleration,βTandβcare the thermal and concentration enlargement coefficients,respectively,τdescribes the ratio between the nanoparticle’s heat capacity and the original fluid heat capacity,DBrepresents the coefficient of Brownian diffusion,DTindicates the thermophoresis diffusion coefficient,∞Cand∞Tare upstream concentration and temperature,respectively,andαis thermal diffusivity.

The suitable boundary conditions for the considered flow problems are

3.Non-similar analysis

We propose the following non-similarity transformations

These transformations identically satisfy the continuity equation(2).Substituting(8)into(3)–(7),we get the following system of dimensionless PDEs

In the above equations,the magnetic parameter(M),secondgrade fluid parameter(α),Richardson number(λ),ratio of mass and heat transfer Grashof numbers(N),Brownian motion(Nb),Prandtl number(Pr),thermophoresis(Nt),and Schmidt number(Sc),respectively,are defined as

4.First truncation system

By using a local similarity technique the terms containing a partial derivative with respect toξare treated as approximately small and considered equal to zero.Therefore,equations(9)–(11)become

The boundary conditions are

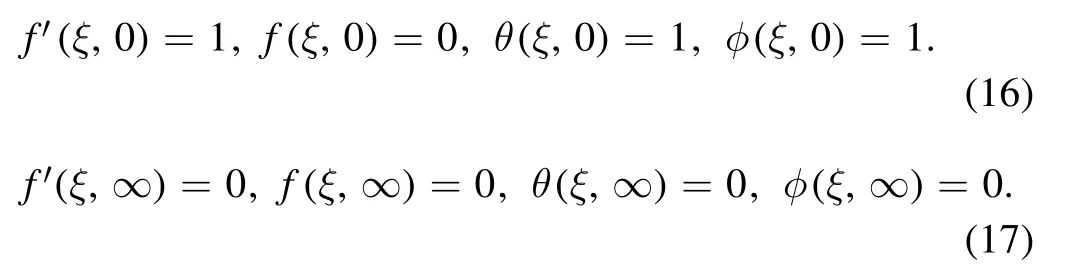
5.Second truncation system

For the second truncation system we considered

Equations(9)–(11)take the following form

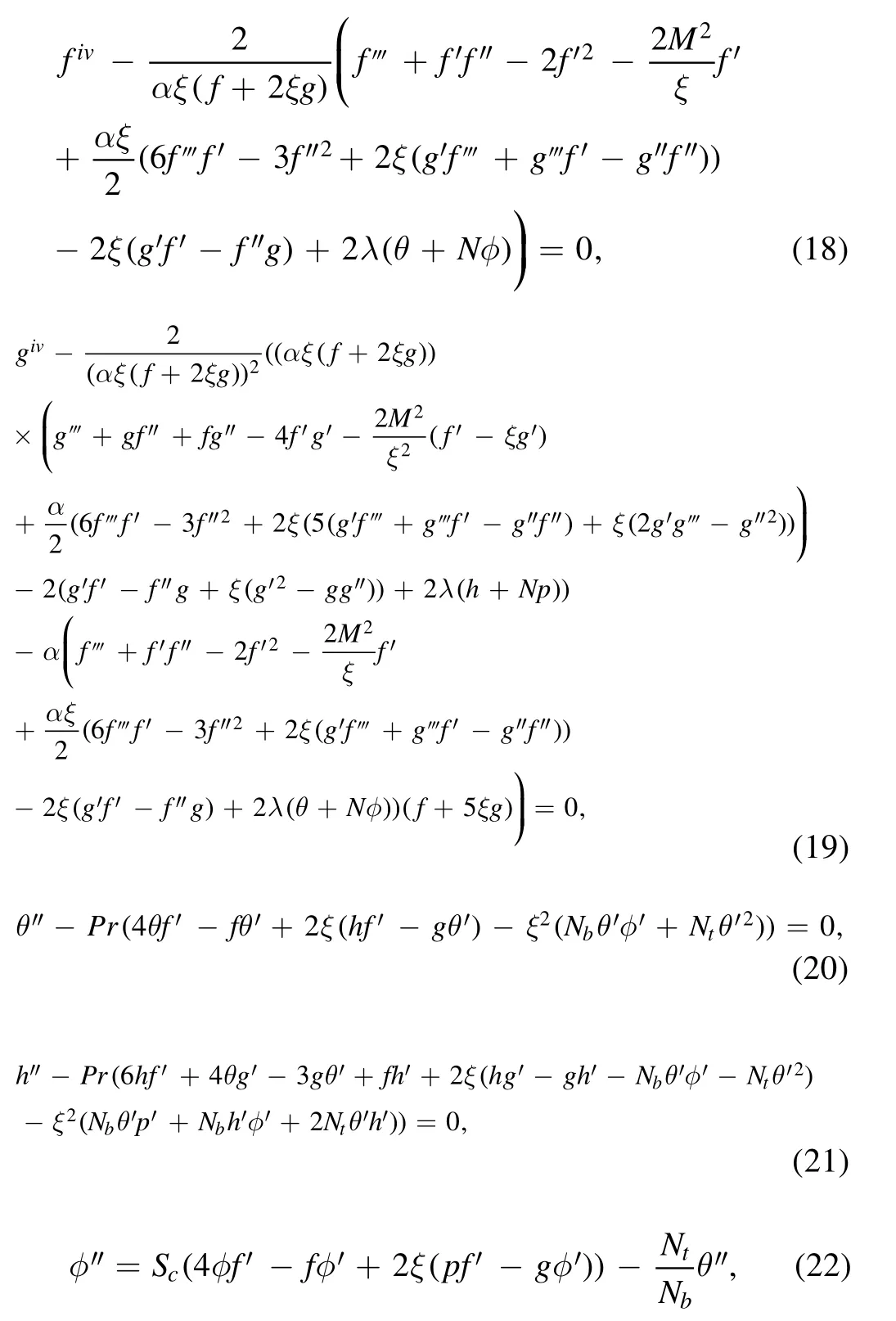
The boundary conditions are

The parameters of physical interest,such as the friction coefficientCf,the local Nusselt numberNuand the Sherwood numberShare defined as,

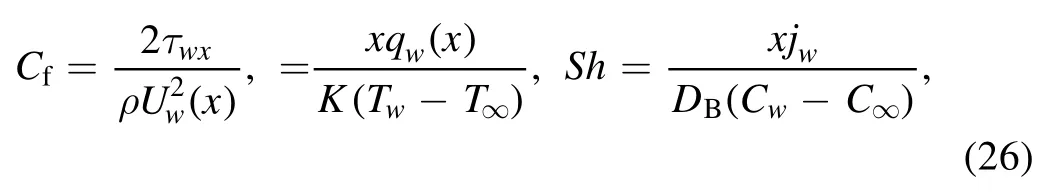
where the wall skin frictionτwx,heat fluxqwand mass fluxjware expressed as

Using(27)in(26)we get,

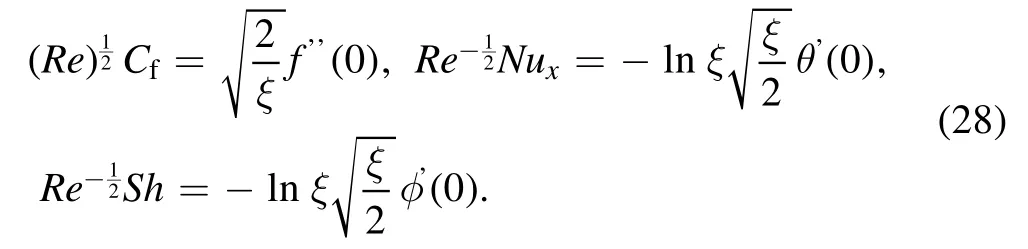
6.Results and discussion

The interpretation of solutions regarding the impacts of the different dimensionless quantities onf′(η),θ(η)andφ(η)arepresented in this section.The variation in the numerical data of the friction coefficient(Cf),Nusselt number(Nu)and Sherwood number(Sh)for numerous values of involved quantities are depicted in this tabular form.The Nusselt number is the ratio of convective to conductive heat transfer,and the Sherwood number is defined as the ratio of the convective mass transfer to the mass diffusivity at a boundary in a fluid.Large values of the Nusselt number show pre-eminence of convection of heat transfer over conduction and small values of the Nusselt number indicate that poor convection occurs.So the Nusselt number indicates the dominant heat transfer phenomenon of the system.Graphical analysis of the velocity,temperature and concentration fields are conferred to explain the current non-similar model.

Table 1 shows the range of governing parameters in which graphical solutions of velocity,temperature and concentration profiles reveal stable behavior.Table 2 depicts the impacts of the magnetic parameter(M),Richardson number(λ),second-grade fluid parameter(α)and ratio of mass and heat transfer Grashof numbers(N)on the local skin friction.We perceive that the friction coefficient decreases marginally asMincreases,while the coefficient of skin friction increases due to increases in the values ofα,λandN.

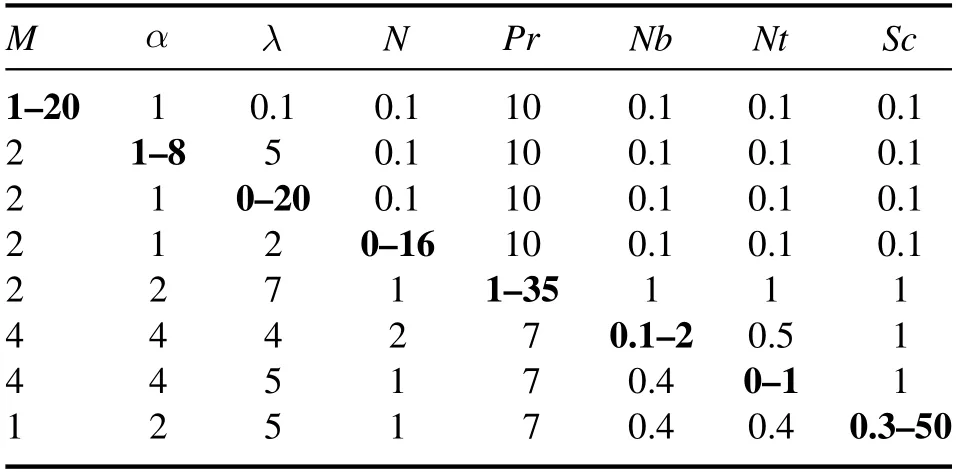
Table 1.The range of defined parameters for a stable solution.

Table 2.Numerical data for the skin friction coefficientfor various parameters.

Table 2.Numerical data for the skin friction coefficientfor various parameters.

?

Table 3 displays the local Nusselt number values for the various governing parameter values.It is established that the rate of heat transfer on the wall increases due to the increase inNb.It is also shown that uplifting the values of the parametersPrandNtresulted in a decline in the numeric values of the local Nusselt number.

Table 3.The local Nusselt numberfor various parameters.

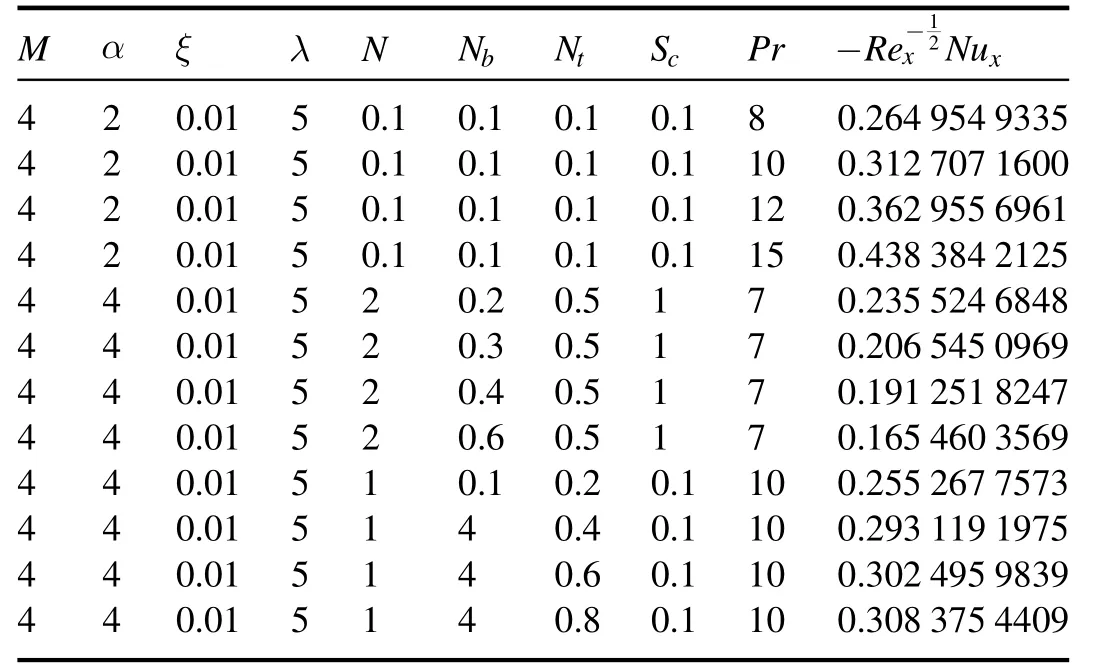
Table 3.The local Nusselt numberfor various parameters.

?

Table 4 describes the impact of governing parameters on the local Sherwood number.The table shows that for increasingNtandScvalues,the local Sherwood coefficient decreases.

Table 4.Numerical data for the local Sherwood numberSh for various parameters.

Table 4.Numerical data for the local Sherwood numberSh for various parameters.

M αξλ N NbNtScPr --Re Sh x 12 22 0.01 51 0.4 0.4 0.270.127 830 7934 22 0.01 51 0.4 0.4 0.470.141 073 9103 22 0.01 51 0.4 0.4 0.670.294 137 7066 22 0.01 51 0.4 0.4 0.870.307 232 1177 22 0.01 51 0.2 0.4 0.170.102 663 3317 22 0.01 51 0.3 0.4 0.170.101 851 7903 22 0.01 51 0.4 0.4 0.170.093 584 0243 22 0.01 51 0.5 0.4 0.170.095 747 2218 22 0.01 51 0.4 0.1 0.170.075 010 4120 22 0.01 51 0.4 0.2 0.170.084 432 5427 22 0.01 51 0.4 0.3 0.170.087 396 3154 22 0.01 51 0.4 0.4 0.170.093 584 0243

Whereas the local Sherwood number increases with the increasing values ofNb.

Figures 2–5 demonstrate the velocity profiles for different parameters likeM,α,λ andN.The consequence of an applied magnetic fieldMin the transverse direction on flow over a stretching sheet is shown in figure 2.It is observed that the increase in magnetic field reduces the fluid velocity.In general,an increase in the applied magnetic field in the transverse direction produces the Lorentz force which opposes the flow.We observed that the Lorentz force effect reduces the flow of the velocity profile.Figure 3 indicates that the fluid flow increases with increasing α,thus thickening the boundary velocity layer.Figures 4 and 5 give an insight into the effect of λ andNon velocity.From figure 4 it is conspicuous that the velocity profile increases with increasing values of λ.Figure 5 indicates that the velocity profile increases with the increasing values ofN(ratio of mass and heat transfer Grashof numbers)due to the buoyancy effect.

Figure 6.θ(η)for several values of‘Pr’.

Figure 6 reveals that the effect of increasing thePris a decrease in the temperature profile.The ratio of momentum diffusivity and thermal diffusivity is specified by the Prandtl number.So,it is clear that the rise inPrdecreases the thickness of the thermal boundary layer.Figure 7 expresses the dimensionless temperature for several values ofNb.It shows that due to a rise in the values ofNb,the temperature profile decreases.From figure 8 it is seen that the temperature profile rises with the increasing values of the thermophoresis parameterNt.

Figure 9 shows the influence of the Schmidt numberScon the mass concentration profile.It is seen that a rise inScleads to a reduction in the concentration boundary layer thickness.Figure 10 explains the impact of the Brownian motion parameterNbon the mass concentration profile.It is evident from the figure that the concentration profile rises with the upsurge in the values ofNb.The influence of the thermophoresis parameterNton the concentration profile is illustrated in figure 11.It is perceived that the concentration profile decreases with the increase inNt.

Figure 7.θ(η)for several values of‘Nb’.

Figure 8.θ(η)for several values of‘Nt’.

Figure 9.φ(η)for several values of‘Sc’.

Figure 10.φ(η)for several values of‘Nb’.

Figure 11.φ(η)for several values of‘Nt’.

7.Conclusions

In this research non-similar modeling is performed for second-grade magnetic nanofluid flow over a vertical surface which is stretching at an exponential rate.Non-similar solutions are obtained through local non-similarity via bvp4c.The important results are mentioned below.

?The velocity profile is increased by the increase inN,λ and α,while the velocity profile decreases as a result of the increase inM.

?The temperature profile is increased due to the increase inNt,although the temperature profile decreases due to the increase inNbandPr.

?The increase in the valueNbleads to the rise in the volumetric concentration profile,while the opposite is true forScandNt.

?Local skin friction increases due to the increase in the values ofα,λandNand slightly decreases as the values of theMincrease.

?It is observed that the local Nusselt number upsurges against theNb,whereas it declines by uplifting thePr andNtparameters.

?The local Sherwood number decreases with the increase inNtandSc,but the effect is the reverse forNb.

ORCID iDs