Remarks on Blow-Up Phenomena in p-Laplacian Heat Equation with Inhomogeneous Nonlinearity
ALZAHRANI Eadah Ahma and MAJDOUB Mohamed
Deapartment of Mathematics,College of Science,Imam Abdulrahman Bin Faisal University,P.O.Box 1982,Dammam,Saudi Arabia&Basic and Applied Scientific Research Center, Imam Abdulrahman Bin Faisal University, P.O.Box 1982,31441,Dammam,Saudi Arabia.
Abstract. We investigate the p-Laplace heat equation ut??pu=ζ(t)f(u)in a bounded smooth domain. Using differential-inequality arguments, we prove blow-up results under suitable conditions on ζ,f, and the initial datum u0. We also give an upper bound for the blow-up time in each case.
Key Words: Parabolic problems; p-Laplacian equation;blow-up;positive initial energy.
1 Introduction
In the past decade a strong interest in the phenomenon of blow-up of solutions to various classes of nonlinear parabolic problems has been assiduously investigated. We refer the reader to the books[1,2] as well as to the survey paper[3]. Problems with constant coefficients were investigated in[4],and problems with time-dependent coefficients under homogeneous Dirichlet boundary conditions were treated in[5]. See also[6]for a related system. The question of blow-up for nonnegative classical solutions ofp-Laplacian heat equations with various boundary conditions has attracted considerable attention in the mathematical community in recent years.See for instance[7–10].
There are two effective techniques which have been employed to prove non-existence of global solutions:the concavity method([11])and the eigenfunction method([12]). The latter one was first used for bounded domains but it can be adapted to the whole space RN. The concavity method and its variants were used in the study of many nonlinear evolution partial differential equations(see,e.g.,[13–15]).
In the present paper, we investigate the blow-up phenomena of solutions to the following nonlinearp-Laplacian heat equation:
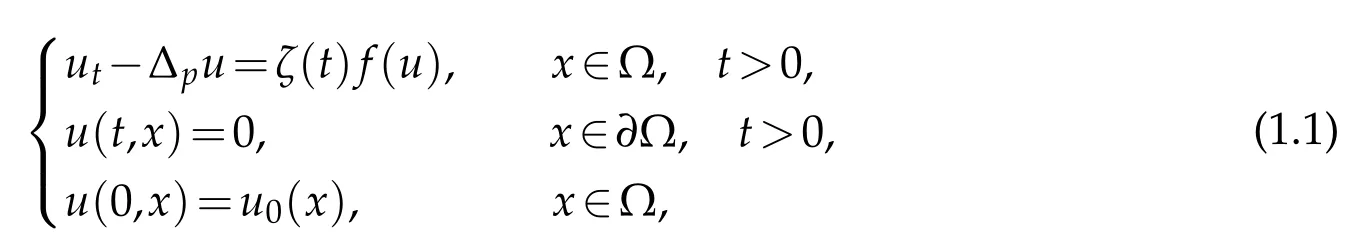
The case ofp=2 has been studied in [4] forζ(t)≡1, and in [5] forζbeing a nonconstant function oft. Concerning the casep>2,Messaoudi[10]proved the blow-up of solutions with vanishing initial energy whenζ(t)≡1. See also[9]and references therein.Recently, ap-Laplacian heat equations with nonlinear boundary conditions and timedependent coefficient was investigated in [7]. This note may be regarded as a complement,and in some sense an improvement,of[5,10].
Let us now precise the assumptions onfandζ. Ifp=2,we suppose either
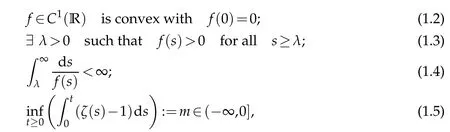
or
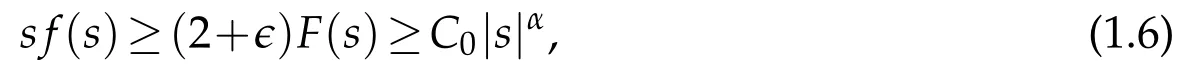
for some constants?,C0>0,α>2,and
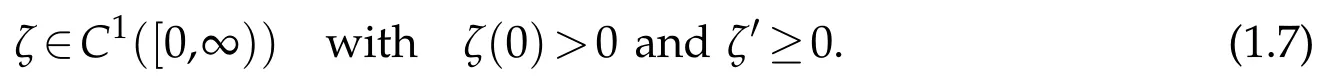
Here
Our first main result concerns the casep=2 and reads as follows.
Theorem 1.1.Suppose that assumptions(1.2)–(1.5)are fulfilled. Let0≤u0∈L∞(?)such thatis large enough. Then the solution u(t,x)of problem(1.1)blows up in finite time.
Remark 1.1.
(i) The functionφ1stands for the eigenfunction of the Dirichlet-Laplace operator associated to the first eigenvalueλ1>0,that is
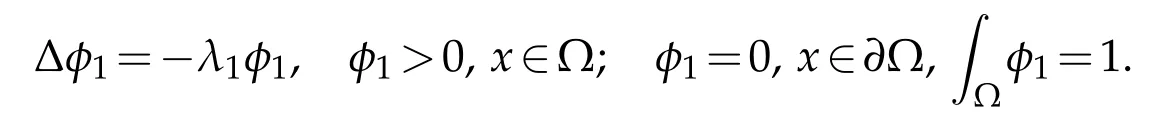
(ii) The assumptions(1.2)–(1.5)onfandζcover the example
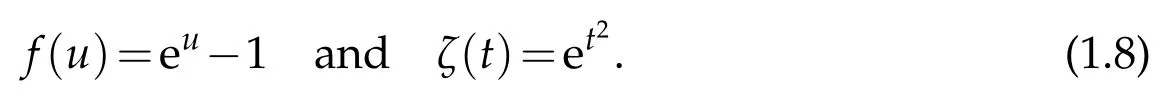
Note that this example is not studied in [5], and Theorem 1.1 can be seen as an improvement of Theorem 1 of[5].
(iii) As it will be clear in the proof below,an upper bound of the maximal time of existence is given by

wheremis as in(1.5)and
(iv) The conclusion of Theorem 1.1 remains valid for ?=RNif we replaceφ1by?(x)=
In order to state our next result(again forp=2),we introduce the energy functional
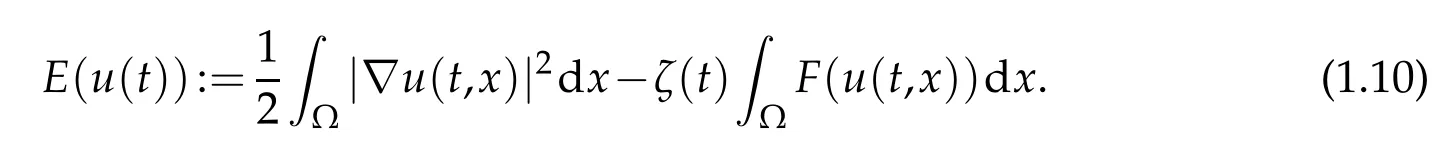
Using (1.7), we see thatis nonincreasing along any solution of (1.1). This leads to the following.
Theorem 1.2.Suppose that assumptions(1.6)-(1.7)are fulfilled. Assume that either E(u0)≤0or E(u0)>0andis large enough. Then the corresponding solution u(t,x)blows up infinite time.
Remark 1.2.An upper bound for the blow-up time is given by
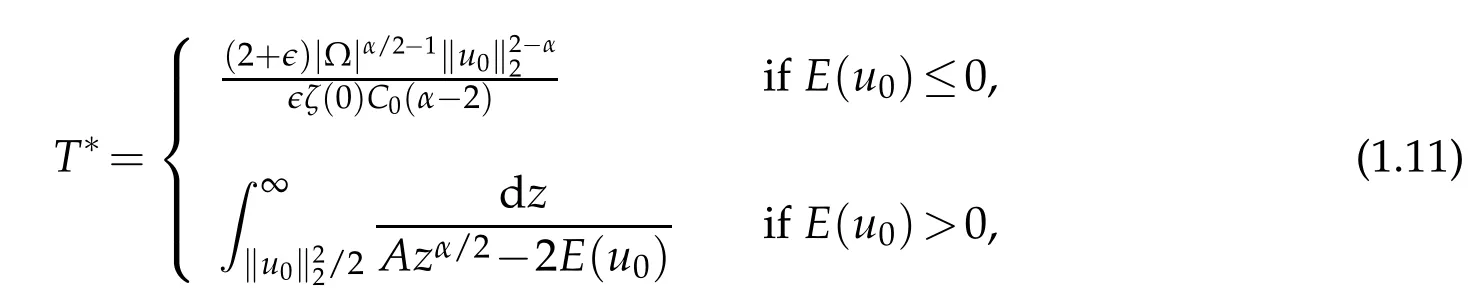
where
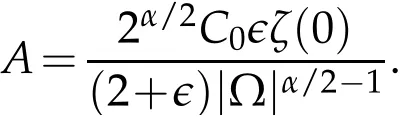
We turn now to the casep>2. In [16], the author studied (1.1) whenζ(t)≡1. He established:
? local existence whenf∈C1(R);
? global existence whenu f(u)|u|qfor someq ? nonglobal existence under the condition Later on Messaoudi[10]improved the condition(1.12)by showing that blow-up can be obtained for vanishing initial energy. Note that by adapting the arguments used in[16],we can show a local existence result as stated below. Theorem 1.3.Suppose ζ∈C([0,∞])and f∈C(R)satisfy|f|≤g for some C1?function g.Thenfor any,the problem(1.1)has a local solution The energy of a solutionuis We also define the following set of initial data Our main result concerningp>2 ca be stated as follows. Theorem 1.4.Suppose that assumption(1.7)is fulfilled. Let f∈C(R)satisfy|f|≤g for some C1-function g and Then for any u0∈Ethe solution u(t,x)of(1.1)given in Theorem1.3blows up in finite time. Remark 1.3.Theorem 1.4 and its proof are almost the result of[10]. In fact,withζsatisfying(1.7),it only accelerate the blow-up. Remark 1.4.Although the proof uses the Poincar′e inequality in a crucial way,we believe that a similar result can be obtained for ?=RN.This will be investigated in a forthcoming paper. We stress that the set E is non empty as it is shown in the following proposition. Proposition 1.1.Suppose that assumption(1.15)is fulfilled and ζ(0)>0. ThenE?. This section is devoted to the proof of Theorems 1.1-1.2-1.4 as well as Proposition 1.1. The main idea in the proof is to define a suitable auxiliary function y(t) and obtain a differential inequality leading to the blow-up. Define the function y(t)as where We compute where we have used a′/a?λ1=?λ1ζ. By using(1.2)and the fact that 0≤a≤1,we easily arrive at Since f is convex and due to(1.4),there exists a constant C≥λ such that f(s)≥2λ1s for all s≥C. Suppose y(0)>C. It follows from(2.4)that,as long as u exists,y(t)≥C. Therefore Hence This means that the solution u cannot exist globally and leads to the upper bound given by(1.9). Lety(t)be the auxiliary function defined as follows We compute whereE(u(t))is given by(1.13). Taking advantage of(1.6),we obtain that Moreover,we compute thanks to(1.7). It then follows thatE(u(t))is non-decreasing intso that we have From(2.5),(2.7),and the H?lder inequality,we find that To conclude the proof we use the following result. Lemma 2.1.Let y:[0,T)→[0,∞)be a C1?function satisfying for some constants C1∈R,C2>0,q>1. Then Proof of Lemma 2.1.We give the proof here for completeness.IfC1≤0 theny′(t)≥C2y(t)q. It follows that Integrating this differential inequality yields the desired upper bound in this case. Suppose now thatC1>0 and.Thenfor all 0≤t Integrating this differential inequality yields This finishes the proof of Lemma 2.1. We define and By using(1.1),we obtain that HenceH(t)≥H(0)≥0,by virtue of(1.7). Recalling(1.1),(2.11),and(1.15),we compute Applying H?lder inequality and then Poincar′e inequality yields whereC>0 is a constant depending only on ? andp. Hence Integrating the differential inequality(2.13)leads to Thereforeublows up at a finite time Recalling(1.15),we obtain that for some constantC>0. LetK?? be a compact nonempty subset of ?. Fix a smooth cut-of functionφ∈C∞(?)such that We look for initial datau0=λφwhereλ>0 to be chosen later. Clearlyu0∈L∞(?)∩and forλ≥1 we have using(2.14) we deduce thatu0∈E forλlarge enough.This finishes the proof of Proposition 1.1. Acknowledgement The authors are grateful to the anonymous referee for a careful reading of the manuscript and for his/her constructive comments.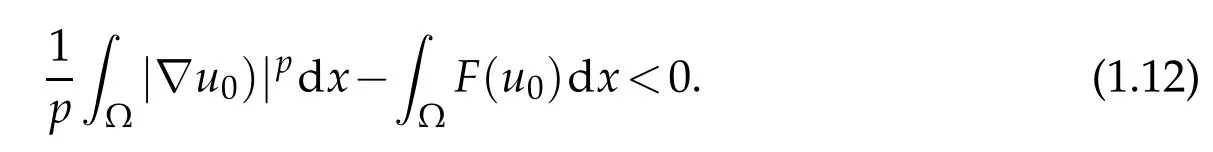
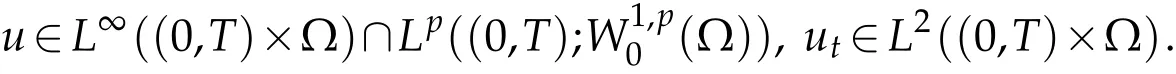
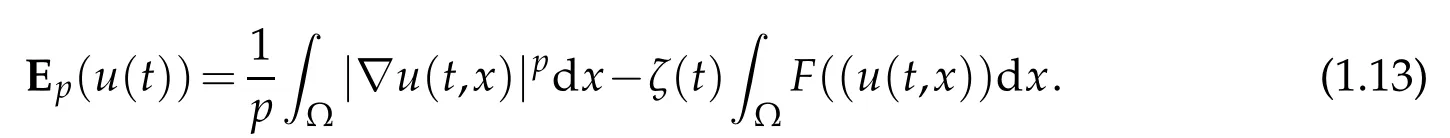

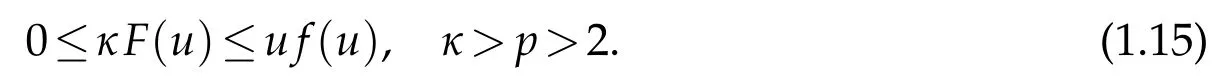
2 Proofs
2.1 Proof of Theorem 1.1
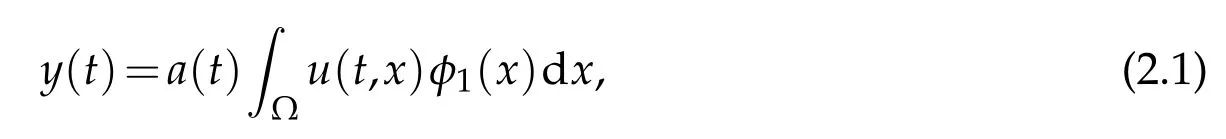

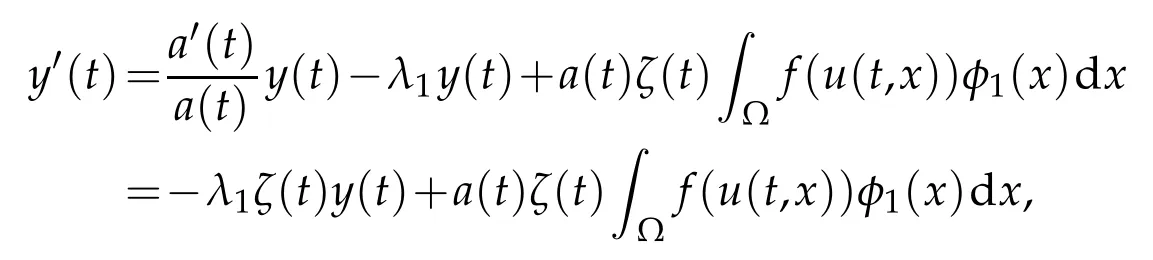
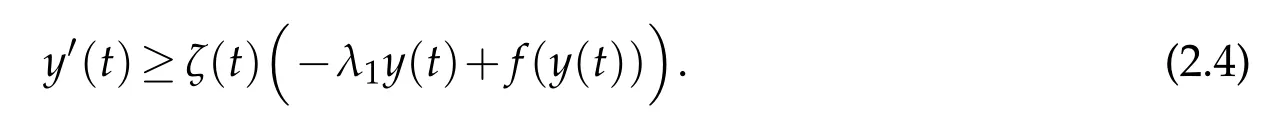

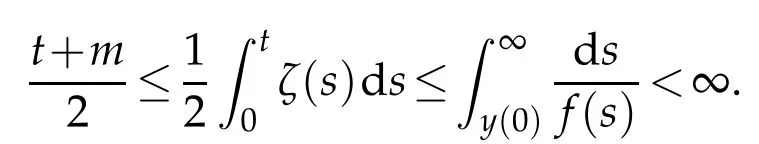
2.2 Proof of Theorem 1.2
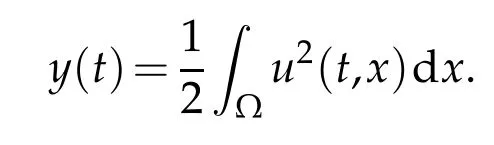

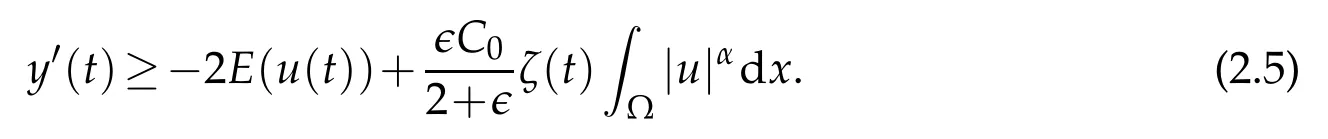
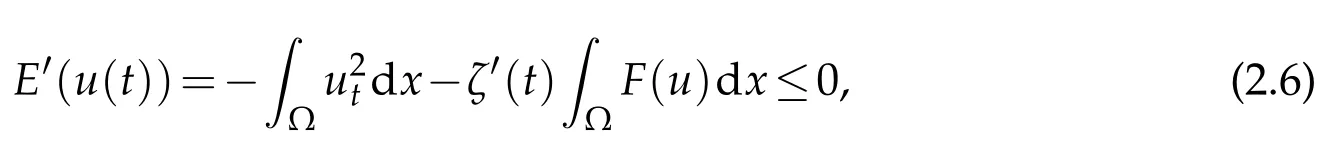
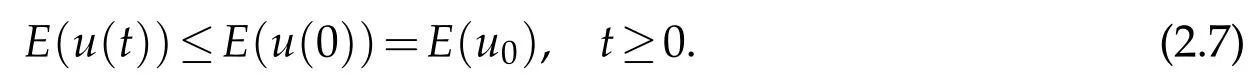
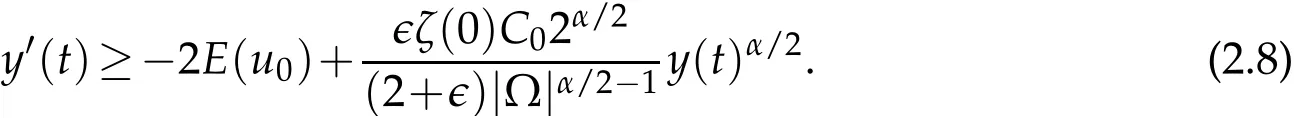

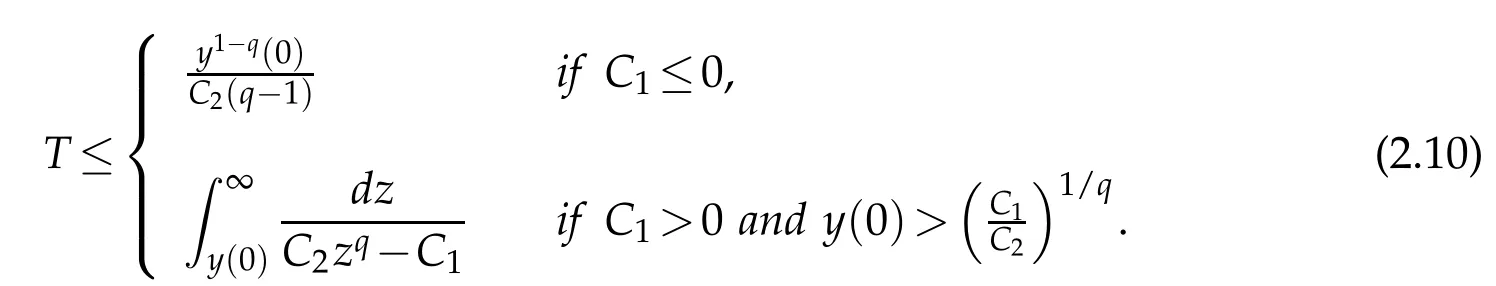
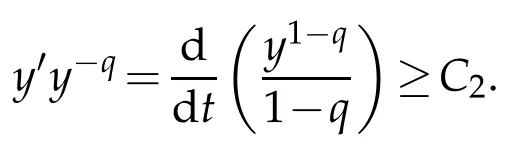

2.3 Proof of Theorem 1.4


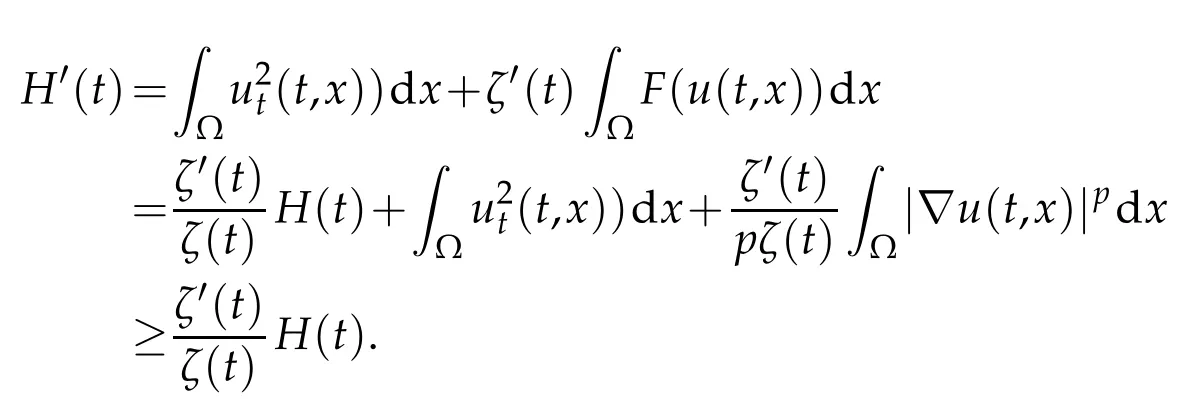
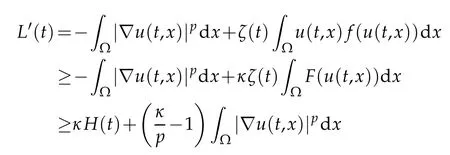



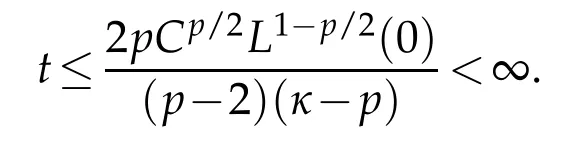
2.4 Proof of Proposition 1.1

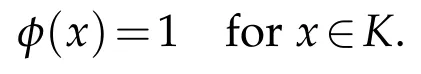
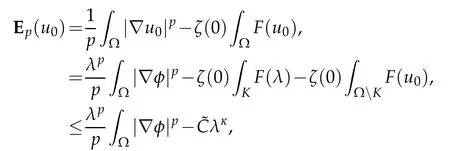

 Journal of Partial Differential Equations2021年1期
Journal of Partial Differential Equations2021年1期
