On Free Boundary Problem for the Non-Newtonian Shear Thickening Fluids
WANG Shu and YUAN Fang,2,?
1 College of Applied Sciences,Beijing University of Technology,Beijing 100124,China.
2 China Everbright Bank,Beijing 100054,China.
Abstract. The aim of this paper is to explore the free boundary problem for the Non-Newtonian shear thickening fluids. These fluids not only have vacuum,but also have strong nonlinear properties. In this paper, a class of approximate solutions is first constructed,and some uniform estimates are obtained for these approximate solutions.Finally, the existence of free boundary problem solutions is proved by these uniform estimates.
Key Words: On free boundary problem;the non-Newtonian shear thickening fluids;vacuum.
1 Introduction
It is well known that the non-newtonian shear thickening flows can be described by the following equations(for example,see[1-6])
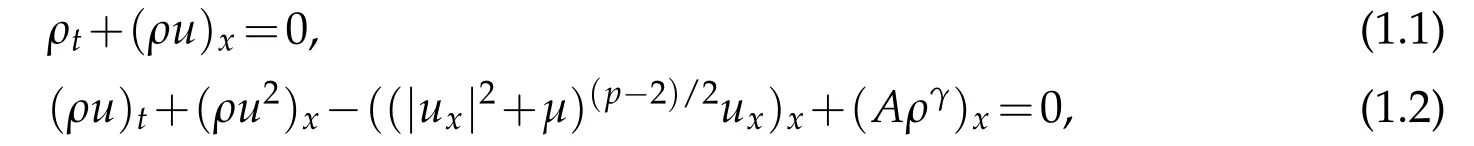
wherep>2,A>0,μ>0 andγ>1 are some given positive constants,andρ,u,ργrepresent the density,velocity and pressure for the non-Newtonian fluids,respectively.
We assume that the initial densityρ0is some given nonnegative function satisfying suppρ0=[a0,b0]for some constantsa0andb0,and||ρ0||L1(a0,b0)=1.Letx=a(t)andx=b(t)represent the free boundary which is the interface between fluid and vacuum, and then haveρ(a(t),t)=ρ(b(t),t)=0,anda′(t)=u(a(t),t)witha(0)=a0,andb′(t)=u(b(t),t)withb(0)=b0.
We introduce the Lagrange coordinate transformation

Clearly, the left dividing line Γ0:x=a(t) for the interface is a straight line Γ0:y=0 in Lagrange coordinates. In addition,in the right dividing line Γ1:x=b(t)for the interface,we have

Therefore, the right dividing line Γ1:x=b(t) for the interface is a straight line Γ1:y=1 in Lagrange coordinates. In particular, in Lagrange coordinates, the original equations(1.1)-(1.2)are transformed into the following equations
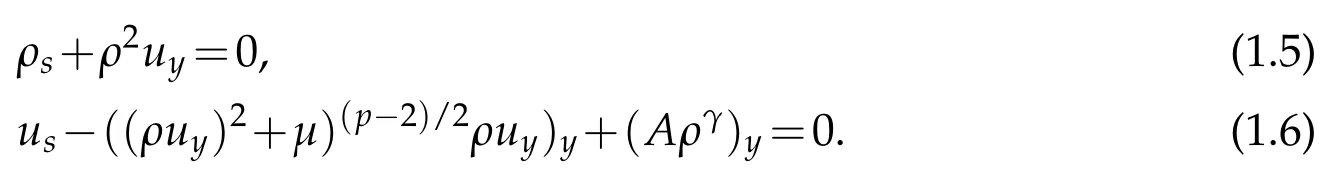
This paper is to solve the above equations(1.5)-(1.6)inQS≡(0,1)×(0,S)(S>0)with the following initial condition
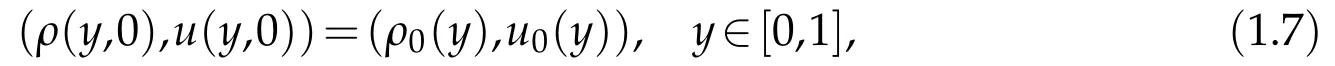
and the following boundary condition
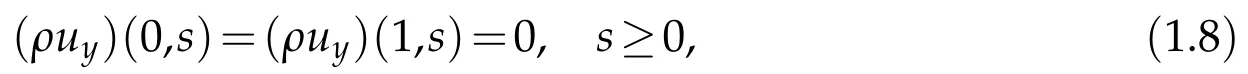
where the initial densityρ0=ρ0(y)and the initial velocityu0=u0(y)have the following properties[A1]-[A3]:
[A1]The initial densityρ0∈C(?∞,+∞)∩C1(0,1)satisfies
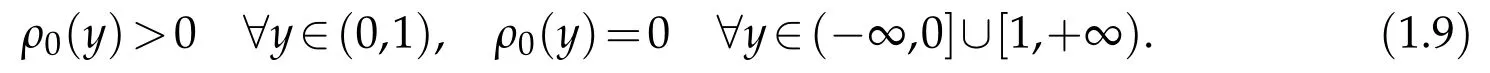
[A2]The initial velocityu0∈C3(?∞,+∞)satisfiesu0y(0)=u0y(1)=0.
[A3]The initial value(ρ0,u0)also has the following property:
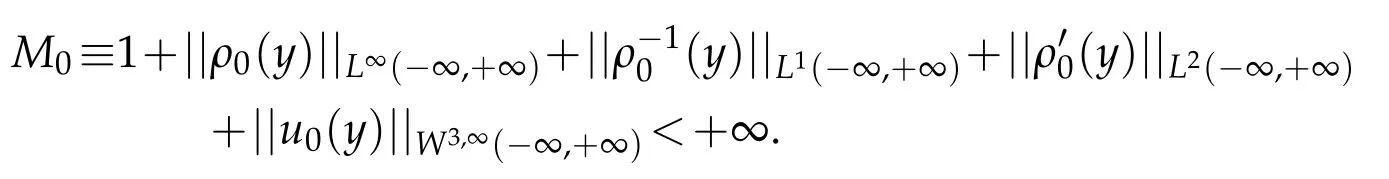
Our main results are the following theorems.
Theorem 1.1.Let p>2and γ>1, and assume that[A1]-[A3]hold. Then there is a positive number S0∈(0,1)such that, the initial-boundary problem(1.5)-(1.8)has at least one solution(ρ,u)=(ρ(y,s),u(y,s))for(y,s)∈QS0. In particular, the solution(ρ,u)also has the following properties:
(i)There exist two positive constantsμ1andμ2depending only on A,p,γ and M0such that
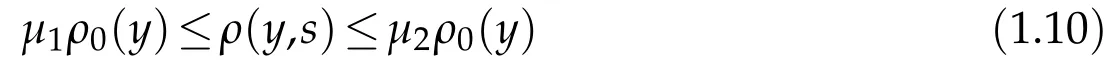
for almost all(y,s)∈QS0.
(ii)The solution(ρ,u)has the following regularity:

(iii)For almost all(y,s)∈QS0,the solution(ρ,u)=(ρ(y,s),u(y,s))satisfies Eqs.(1.5)-(1.6).
(iv)For almost all s∈(0,S0),the solution(ρ,u)satisfies initial conditions(1.7)in the following sense:
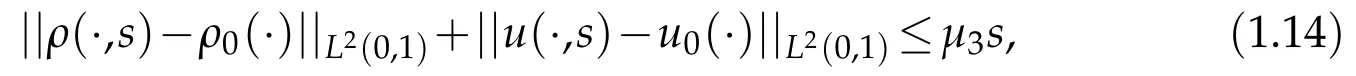
whereμ3is a positive constant depending only on A,p,μ,γ and M0.
(v)For almost all(y,s)∈QS0, the solution(ρ,u)satisfies boundary condition(1.8)in the following sense:
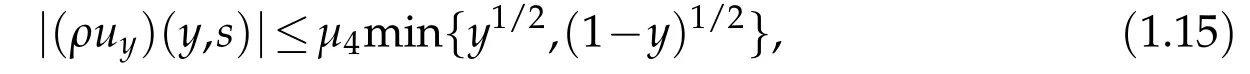
whereμ4is a positive constant depending only on A,p,μ,γ and M0.
We shall prove Theorem 1.1 in Section 4. In order to prove Theorem 1.1, we need some Lemmas in Sections 2-3.
2 Fundamental lemmas
In order to prove our results,we need following Lemmas.
Lemma 2.1.Let0

for all r∈(?∞,+∞). Then we have
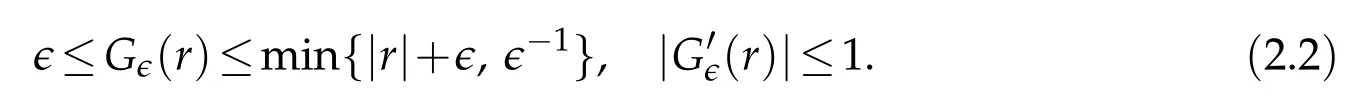
In addition,for any q>0,we also have
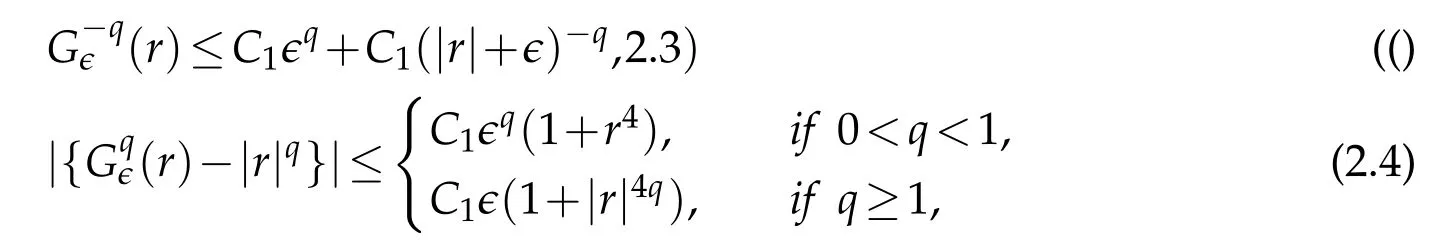
where C1is a positive constant depending only on q.
Proof.The conclusions(2.2)-(2.3)of Lemma 2.1 can be obtained by direct calculation. For(2.4),we have two cases:(i)0 To prove(2.4)in the case: (i)0 By(2.2),we have for|r|≤?. For|r|≥?,by(2.5),we compute Combining the above inequality with(2.6) we have(2.4) in the case 0 Lemma 2.2.We define for all r∈(?∞,+∞)and all η∈(0,1),where j∈C∞0(?∞,+∞)is a nonnegative function satisfying In addition,we also define where m=1/4,and Then we have In addition,for any ?∈(0,?0),we have where ?0∈(0,1/2)and C2∈(1,+∞)are some positive constants depending only on p and M0. Proof.From(2.7)-(2.10),the conclusion(2.11)-(2.13)can be obtained by direct calculation.Therefore,the details of the proofs for(2.11)-(2.13)are omitted. To prove(2.14). In fact,by(2.7)-(2.10),fory∈[0,1],we compute By the above inequality,we can obtain(2.14)and(2.15). Thus the proof of Lemma 2.2 is completed. Lemma 2.3.Let ?∈(0,1). We denote for all y∈(?∞,+∞),and then have In addition,we also have where C3is a positive constant depending only on M0. Proof.From (2.16), the conclusions (2.17)-(2.18) can be obtained by direct calculation.Therefore, the details of the proof for Lemma 2.3 are omitted. Thus the proof of Lemma 2.3 is completed. Lemma 2.4.Assume that{hn(s):n=1,2,···}is a sequence of nonnegative continuous functions satisfying the following inequalities for all s∈(0,1)and all n=1,2,···, where C4and C5are some given nonnegative real numbers.Then we have for all s∈(0,1)and all n=1,2,···,where C6=sups∈(0,1)h1(s). Proof.Applying the mathematical induction method,we immediately get for alls∈(0,1) and alln=1,2,···. This implies (2.19). Thus the proof of Lemma 2.4 is completed. Lemma 2.5.We define a function for all r∈(?∞,+∞). Then we have where ν1and ν2are some positive constants depending only onμand p. Proof.From (2.20), the conclusions (2.21)-(2.22) can be obtained by direct calculation.Therefore, the details of the proof of Lemma 2.5 are omitted. Thus the proof of Lemma 2.5 is completed. Byρ?0defined by Lemma 2.2 andu?0defined by Lemma 2.3, we construct a sequence of the approximate solutions as follows. Step 1. We defineρ0=ρ?0and then consider the following initial-boundary problem By[7],the initial-boundary problem(3.1)has a unique smooth solutionu1=u1(y,s). Step 2. We consider the following initial value problem Clearly,the initial value problem(3.2)has a smooth solutionρ1=ρ1(y,s). Step 3. We consider the following initial-boundary problem By[7], the initial boundary problem (3.3) has a unique smooth solutionu2=u2(y,s). In addition,we also consider the following initial value problem Clearly,the initial value problem(3.4)also has a smooth solutionρ2=ρ2(y,s). Repeating the above process we can find a sequence{(ρn,un)}∞n=1of the approximate solutions,which are smooth and satisfy the following equations with initial conditions and boundary conditions where Using[A1]and(2.14),by(3.5),we have Next, we shall find some uniform estimates of approximate solutionsWe have the following lemmas. Lemma 3.1.Let p>2. For any positive integer k,we define where Then,for all n=1,···,k,and all(y,s)∈[0,1]×[0,Sk],and ?∈(0,Sk],we have whereμ1,μ2and C7are some positive constants depending only on A,p,γ and M0. Proof.By(3.13)-(3.14),using Lemma 2.2,we compute Similarly to the above inequality,we also haveρn≥C?1(ρ0(y)+?m).Therefore,we have(3.16). From(3.16),by[A3],we get(3.17). Thus the proof of Lemma 3.1 is completed. Lemma 3.2.Let p>2and denote whereμ1and C1are defined by Lemma3.1and Lemma2.1,respectively. Then,for all n=1,···,k,and all(y,s)∈[0,1]×[0,S1k],and ?∈(0,S1k),we have where C8is a positive constant depending only on A,p,μ,γ and M0. Proof.By Lemmas 2.1 and 3.1,we compute which implies that Then,forn=1,···,kand?∈(0,S1k),by(3.21),we have By(3.21)and(3.22),using Lemma 3.1 we get In addition,by Lemma 3.1,we compute Combining the above inequality with(3.22)-(3.23) we have (3.19)-(3.20). Thus the proof of Lemma 3.2 is completed. Lemma 3.3.Let p>2and γ>1. For all n=1,···,k,and all(y,s)∈[0,1]×[0,Sk],and ?∈(0,S1k),we have where C9is a positive constant depending only on A,p,μand γ. Proof.By Lemmas 2.1 and 3.1,we compute which implies(3.25). By Lemma 2.5 and Lemma 3.1,we compute which implies(3.25). Thus the proof of Lemma 3.3 is completed. Lemma 3.4.Let1 where C10is a positive constant depending only on A,p,μ,γ and M0. Proof.By(3.5)-(3.6)and(3.9)-(3.11),we compute which implies where By(3.25),for alls∈(0,1),we have We now calculate the items on both sides of(3.31). By(3.8)and(3.11),we have By(3.12)and(3.32),using Lemma 2.2 we get By(3.9)-(3.11)and(3.32)-(3.33),we obtain This implies Similarly to(3.35),we also have Applying(3.35)-(3.36),we compute Using Young’s inequality we compute Combining(3.37)-(3.38)with(3.31)we conclude that We now calculate the two items on the right side of(3.39). First,applying Lemma 2.1,Lemma 2.5 and Lemma 3.1,by(3.28)-(3.30),we compute which implies By(3.40)and[A3],using Lemma 3.1 we get fors∈[0,S1k],whereCis a positive constant depending only onA,p,μ,γandM0. Finally, let us calculate the second item on the right side of(3.39). Using(3.9)-(3.11),we compute we compute By the above inequality and(3.7),using Lemma 2.2-2.3,we compute By the above inequality,using Lemma 2.2 we have for alls∈(0,S1k), whereCis a positive constant depending only onA,p,μ,γandM0.Combining (3.41)-(3.42) with (3.39) we get (3.26). Thus the proof of Lemma 3.4 is completed. Lemma 3.5.Let p>2and γ>1. For all n=1,···,k,and all(y,s)∈[0,1]×[0,S1k],and ?∈(0,S1k],we have where C11is a positive constant depending only on A,p,γ,μand M0. Proof.Applying Lemma 3.4,by(3.34),we compute which implies On the other hand,using Lemmas 3.1 and 3.3,we have In addition,by(3.9)and(3.44)-(3.45),we get By(3.46),using Lemma 2.5 we get By(3.47),using Lemma 3.2 we get By(3.48),using Lemma 3.1 we have Using(3.44)-(3.49)we have(3.43). Thus the proof of Lemma 3.5 is completed. Lemma 3.6.Let p>2and γ>1. For all n=1,···,k,and all(y,s)∈[0,1]×[0,S1k],and ?∈(0,S1k],we have where C12is a positive constant depending only on A,p,μ,γ and M0. Proof.By(3.5),using Lemmas 3.1 and 3.5,for alln=1,···,k,and all(y,s)∈(0,1)×(0,S1k),and?∈(0,S1k),we have In addition,by(3.5),for alln=1,···,k,and alls∈(0,S1k),and?∈(0,S1k),we also have By[A3]and Lemma 2.2,we have Using Schwarz’s inequality and applying Lemmas 2.5,3.1 and 3.5,by(3.9),we compute Using the above inequality,by(3.52)-(3.53),we conclude that for alls∈(0,S1k), whereC13is a positive constant depending only onA,p,μ,γandM0.Applying Gronwall’s inequality,by(3.54),we have By the above inequality and(3.54),we conclude that for alln=1,2,···, and alls∈(0,S1k), whereCis a positive constant depending only onA,p,μ,γandM0. Applying Lemma 2.4,by(3.51)and(3.55),we get(3.50). Thus the proof of Lemma 3.6 is completed. Lemma 3.7.Let p>2and γ>1. For all n=1,···,k,and all(y,s)∈[0,1]×(0,S1k],and ?∈(0,S1k],we have where C14is a positive constant depending only on A,p,γ and M0. Proof.By(3.6)and[A3],using Lemmas 2.3 and 3.5,we compute which implies By Lemmas 3.1 and 3.5,we get By(3.6)and Lemma 3.4,we have By(3.58)and[A3],we have Combining(3.57)-(3.60)we get(3.56). Thus the proof of Lemma 3.7 is completed. Lemma 3.8.Let p>2and γ>1. For all n=1,···,k,and all(y,s)∈[0,1]×[0,S1k],and ?∈(0,S1k],we have where C15is a positive constant depending only on A,p,μ,γ and M0. Proof.From Lemmas 2.2-2.3 and Lemmas 3.6-3.7,we compute which implies(3.61). Thus the proof of Lemma 3.8 is completed. Lemma 3.9.Let p>2and γ>1. For all n=1,···,k,and all(y,s)∈[0,1]×[0,S1k],and ?∈(0,S1k],we have where C16is a positive constant depending only on A,p,μ,γ and M0. Proof.Applying Lemmas 2.5 and 3.5,we compute By the above inequality and Lemma 3.3,we get On the other hand,by(3.9)-(3.10),using Lemma 3.4 and Lemma 3.6 we have which implies By(3.63)-(3.64),we have Similar to(3.65),we also have Combining(3.65)-(3.66)and applying Lemma 3.1,we get(3.62).Thus the proof of Lemma 3.9 is completed. In order to prove Theorem 1.1 we need the following lemmas. Lemma 4.1.Let p>2and γ>1,and denote where ?1is defined by Lemma3.2, α is defined by(3.15), C7is defined by Lemma3.1, C11is defined by Lemma3.5. Then,for any positive integer k,we have Proof.For any given positive integerk, by(3.13)-(3.15), we only have two cases: Case I:Sk≥?1,Case II:Sk∈(0,?1). We now prove(4.2)in the Cases I and Case II,respectively. Case I:Sk≥?1. In this case,we have(4.2),and then Lemma 4.1 in the Case I is proved. Case II:Sk∈(0,?1). In this case,by(3.14)and(3.18),we have Applying Lemmas 3.1 and 3.5,by the above equation,we get which implies(4.2). Therefore,Lemma 4.1 in the Case II is also proved. Combining Case I with Case II,we have(4.2)and then the proof of Lemma 4.1 is completed. Lemma 4.2.Let p>2and γ>1. Then,for S0defined by Lemma4.1,there exist and ρ?∈L∞(0,S0;L2(0,1))such that strongly in L∞(0,S0;L2(0,1))∩L2(0,S0;H1(0,1))as n→∞,and strongly in L∞(0,S0;L2(0,1))as n→∞. In addition,we have weakly in L2(QS0)as n→∞. In particular,for almost all(y,s)∈QS0,we also have whereμ1,μ2,C7are defined by Lemma3.1,C12and C14are defined by Lemma3.6and Lemma3.7,respectively. Proof.Denote By(3.5)-(3.6),we have which implies By the above equation,we have Applying Young’s inequality and using Lemmas 2.1, 2.5 and 3.5, by (3.9)-(3.11), we compute which implies Combining(4.10)-(4.11)with(3.7)we get This implies that for alls∈[0,S0],whereC17is a positive constant independent ofn. Applying Gronwall’s inequality,by(4.12),we obtain By(4.12)-(4.13)we have for alls∈(0,S0),whereC18is a positive constant independent ofn. Applying Lemma 2.5,by(4.14),we get where Applying Lemma 3.1,by(4.9)and(4.15)-(4.16),we conclude that for all positive integern, whereCis a positive constant independent ofn. Combining(4.14)with(4.17)we get for alls∈[0,S0], whereCis a positive constant independent ofn. This implies that, the sequence{ρn}∞n=1is a Cauchy’s sequence inL∞(0,S0;L2(0,1)). Therefore,we have (4.4).Similarly,we also have(4.3). In addition,applying Lemma 3.4,Lemmas 3.7-3.8,by(4.3)-(4.4),we have(4.5)-(4.8). Thus the proof of Lemma 4.2 is completed. Lemma 4.3.Let p>2and γ>1. Then,for S0defined by Lemma4.1,we have strongly in L2(QS0)as n→∞, where R?=AGγ?(ρ?), F?=Ψ??R? andΓ?=G?(ρ?)u?y. In addition,we also have weakly in L2(QS0)as n→∞. In particular,we also have for almost all(y,s)∈QS0,where C20is a positive constant depending only on A,p,μ,γ and M0. Proof.By Lemma 2.4,we compute By the above inequality,applying Lemma 4.2, we get.Similarly,we also have Therefore we have(4.18). In addition,from the lower half continuity of the norm,using Lemma 3.5, by (4.18), we get (4.20). Using Lemma 3.4 and Lemma 3.6-3.7, by (3.9), we have whereCis a positive constant depending only onA,p,μ,γandM0. In addition, by the above inequality and (4.19), from the weak lower half continuity of the norm, we get(4.21). Thus the proof of Lemma 4.3 is completed. Lemma 4.4.Let p>2and γ>1. Then,for S0defined by Lemma4.1,there exist(ρ,u)∈L∞(QS0)and a subsequencesuch that strongly in L2(QS0)as ?=?j→0+. In addition,we also have weakly in L2(QS0)as ?=?j→0+,and weakly inas ?=?j→0+. In particular, for almost all(y,s)∈QS0, we alsohave where μ1,μ2and C7are defined by Lemma3.1; C12and C14are defined Lemma3.6and Lemma3.7,respectively. Proof.From the lower half continuity of the norm, applying Sobolev’s imbedding theorem(see,e.g.,[8]), by Lemma 4.2, we have(4.22)-(4.27). Thus the proof of Lemma 4.4 is completed. Lemma 4.5.Let p>2and γ>1. Then,for S0defined by Lemma4.1,we have weakly in L2(QS0)as ?=?j→0+. In particular,we also have for almost all(y,s)∈QS0,where C11is defined by Lemma3.5. Proof.We define for allr∈(0,1). By[A1]and(4.28),for anyr∈(0,1),we have For any givenand for allν∈(0,1),by(4.30)-(4.31),applying Lemmas 4.3-4.4,we compute which implies that for allν∈(0,1), whereCis a positive constant independent of?andν. In the above inequality,letting?=?j→0+andν→0+in turn,using Lemma 4.4,we get for allφ∈L2(QS0). This implies(4.28). From the weak lower half continuity of the norm,by(4.20)and(4.28),we get(4.29). Thus the proof of Lemma 4.5 is completed. Lemma 4.6.Let p>2and γ>1. Then,for S0defined by Lemma4.1,we have strongly in L2(QS0)as ?=?j→0+. Proof.For any givenδ∈(0,1/4),we define a cutoff functionξδ∈C∞0(?∞,+∞)such that whereC21is an absolute constant independent ofδ. Applying Lemma 2.5, Lemmas 4.2-4.5,by(4.33),for any givenδ∈(0,1/4),we compute which implies that By(4.34),using Lemma 2.5,we compute Combining the above inequality with(4.34)we get whereCis a positive constant independent of?andδ. In the above inequality, letting?=?j→0+andδ→0+in turn,using Lemmas 4.4-4.5,we get which implies(4.32). Thus the proof of Lemma 4.6 is completed. Lemma 4.7.Let p>2and γ>1. Then,for S0defined by Lemma4.1,we have strongly in L2(QS0)as ?=?j→0+. In addition,we also have weakly in L2(QS0)as ?=?j→0+. In particular,we also have for almost all(y,s)∈QS0,where C20is defined by Lemma4.3. Proof.Applying Lemma 2.1,Lemmas 4.2-4.3,forξδdefined by(4.33),we compute which implies whereCis a positive constant independent of?andδ. In(4.38), letting?=?j→0+andδ→0+in turn,by Lemma 4.6,we get Using Lemmas 4.3-4.4,we compute By the above inequality and(4.39),we have Similar to(4.40),we also have Combining(4.41)with(4.39)-(4.40) we have(4.35). From the weak lower half continuity of the norm, by Lemma 4.3 and (4.35), we have (4.36)-(4.37). Thus the proof of Lemma 4.7 is completed. Now,let us prove the Theorem 1.1. In fact,the conclusions(i)-(ii)of Theorem 1.1 can be obtained by using Lemma 4.4. To prove the conclusion(iii)of Theorem 1.1,we choose anyφ∈L2(QS0),by(3.6),we have Lettingn→∞in the above equation,by Lemma 4.2-4.3,we get In addition,letting?=?j→0+in the above equation,by Lemma 4.4 and Lemma 4.7,we get for allφ∈L2(QS0). This implies for almost all(y,s)∈QS0. Similarly,we also have for almost all(y,s)∈QS0. Combining(4.42)-(4.43) we get the conclusion(iii)of Theorem 1.1. The conclusions(iv)-(v)can be obtained by Lemmas 3.8-3.9 and Lemmas 4.2 and 4.4,and the details are omitted here. Thus the proof of Theorem 1.1 is completed. Acknowledgement This work is supposed by NSFC(no.11771031 and no.11531010)China.
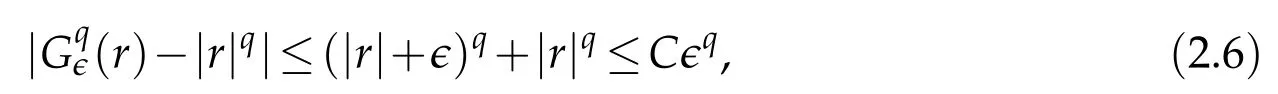
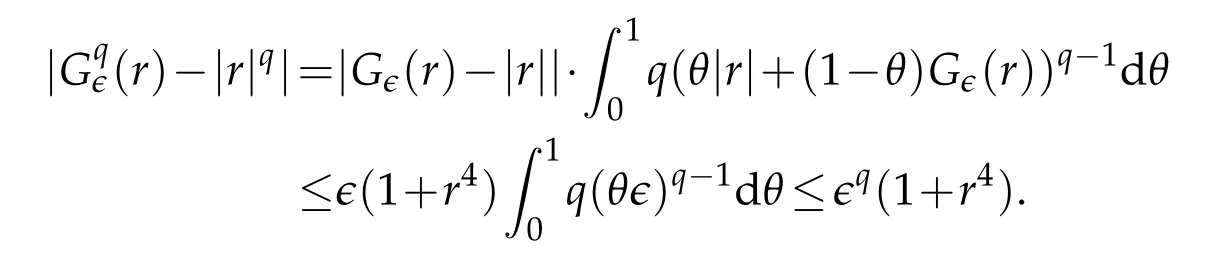

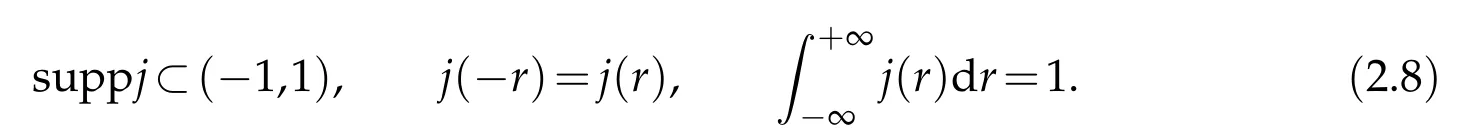

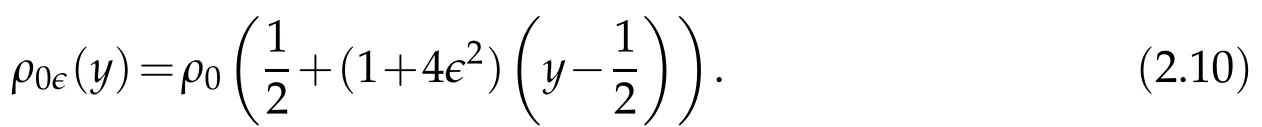
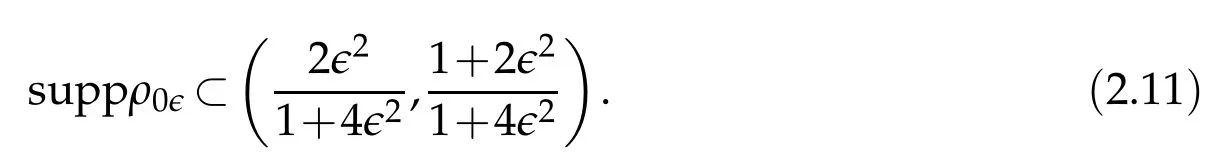

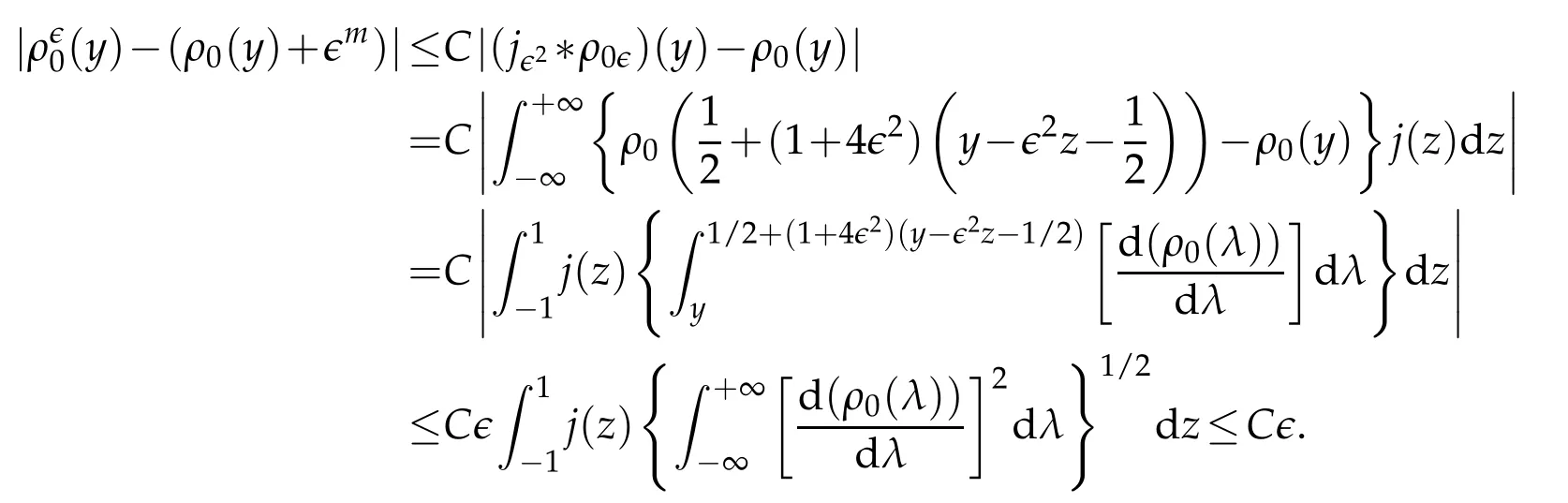
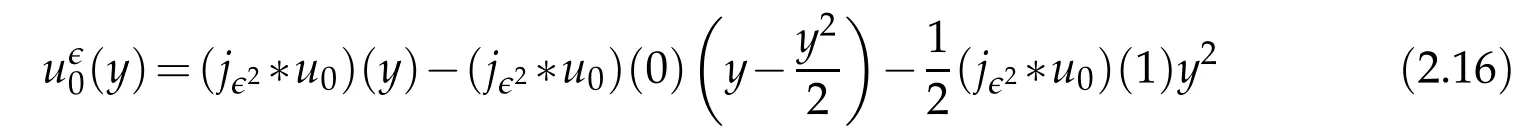

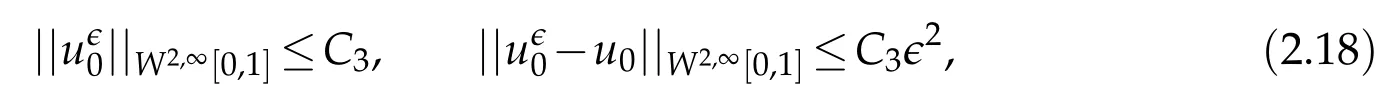
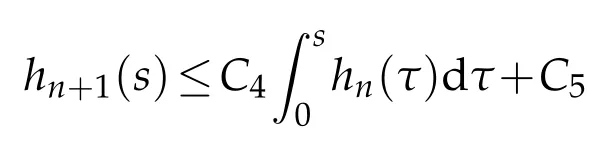
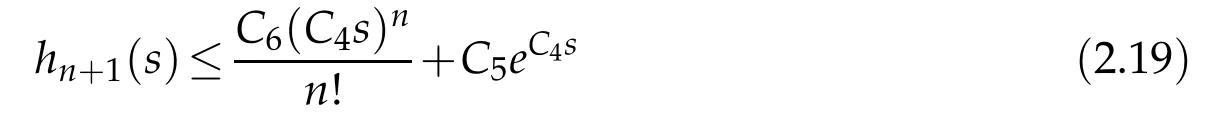
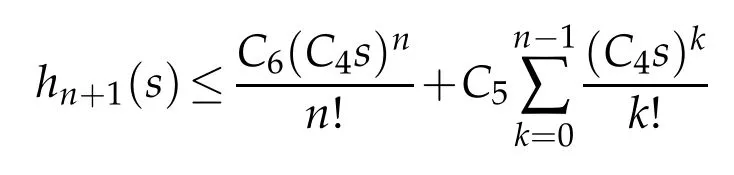


3 The constructions and uniform estimates of the approximate solutions
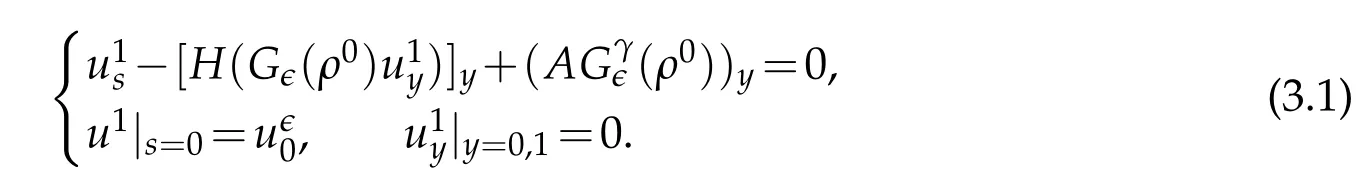

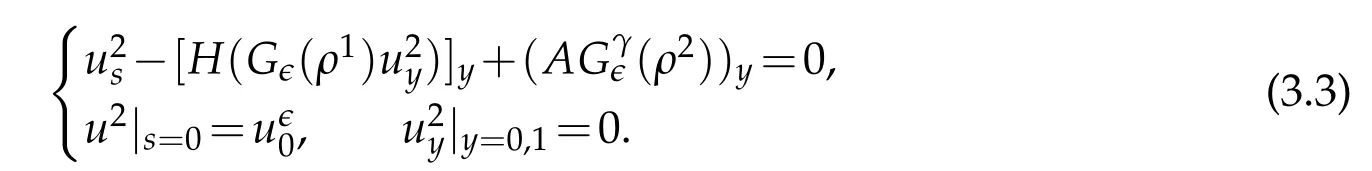




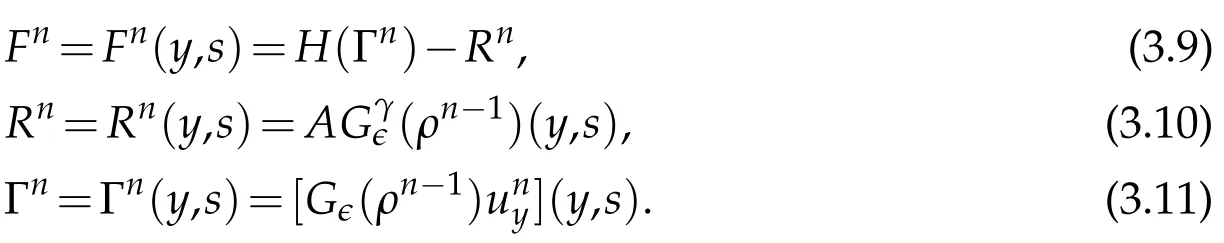
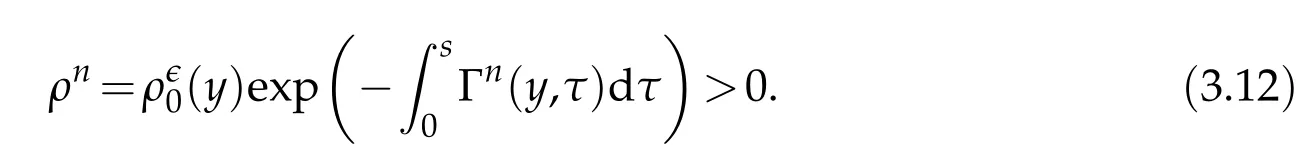
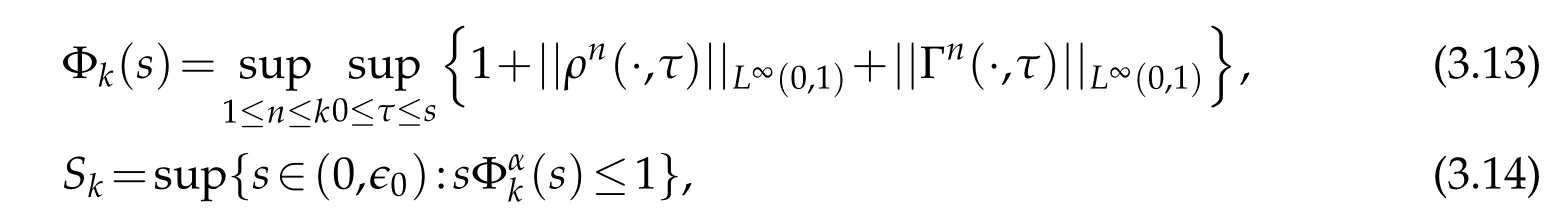

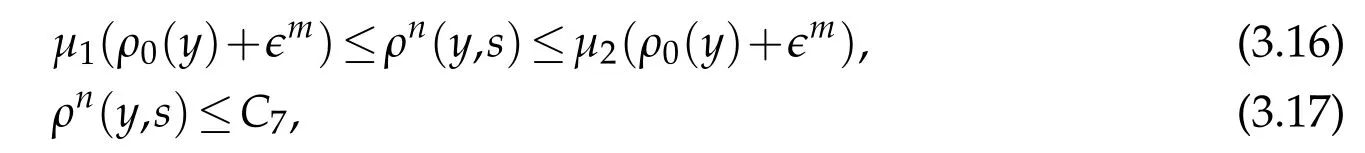
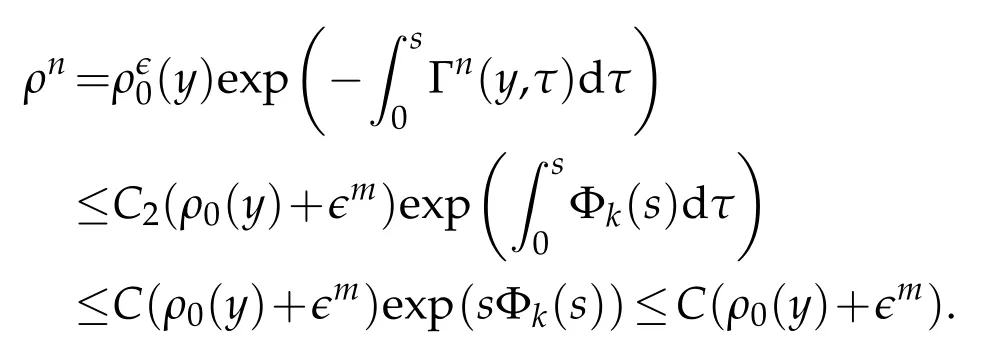
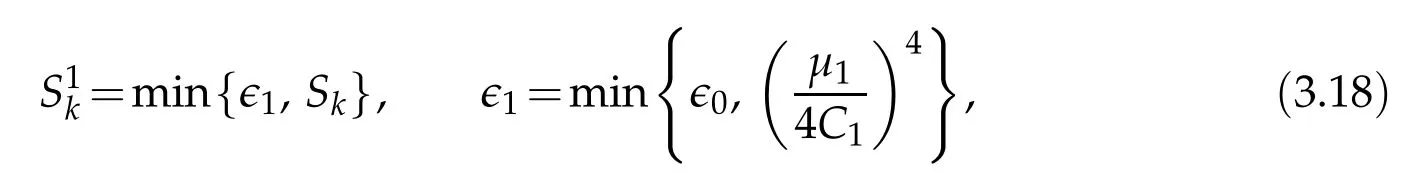
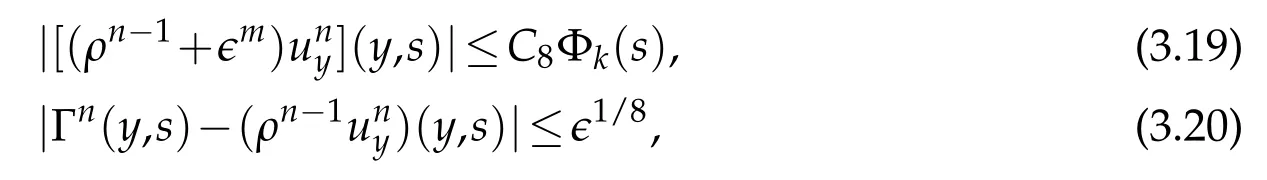
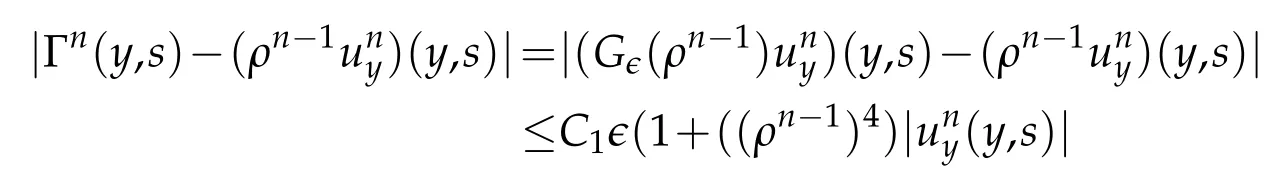
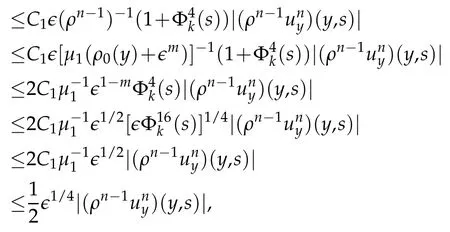

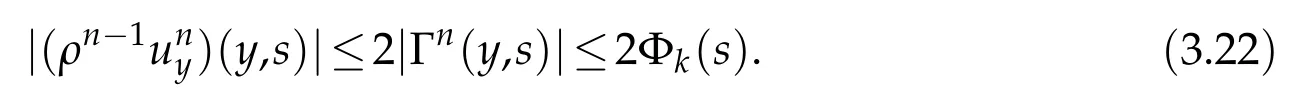
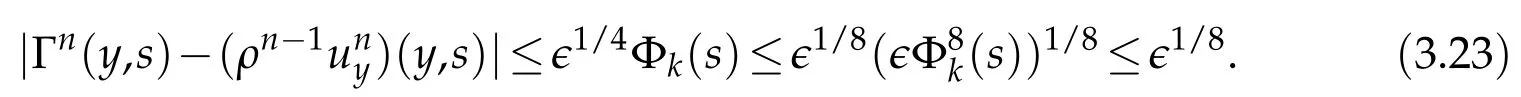
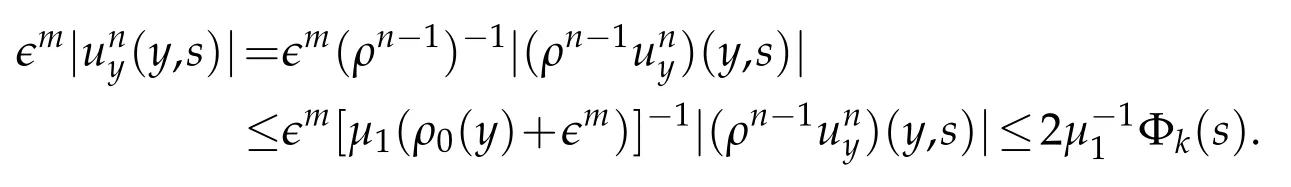
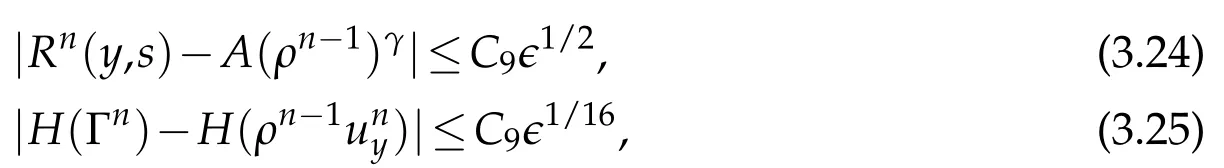
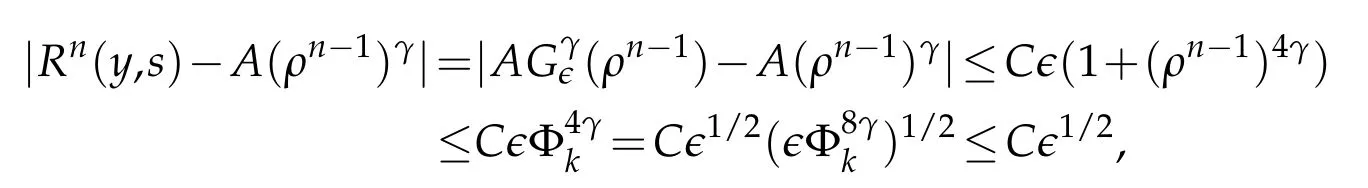
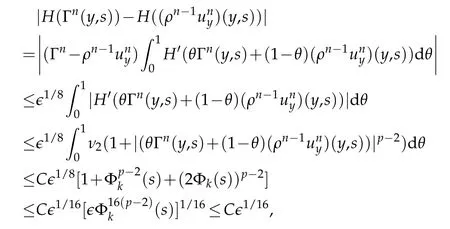

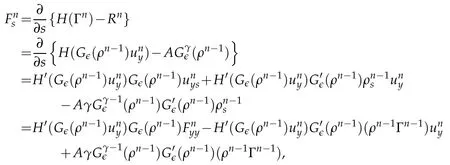

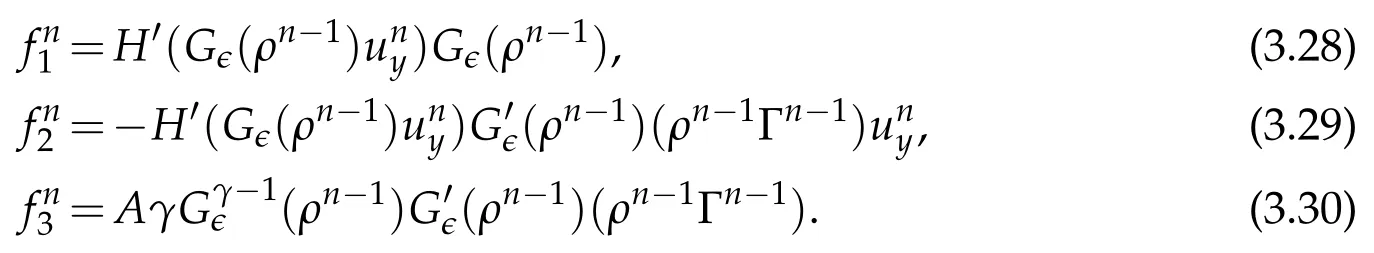
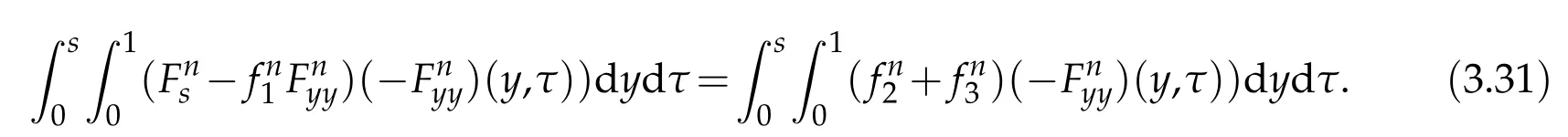
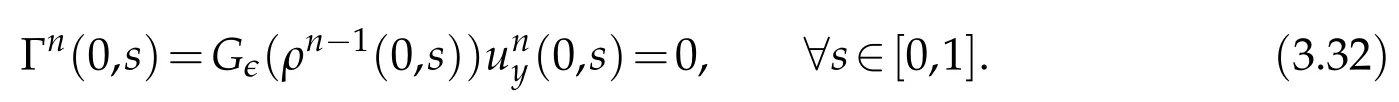
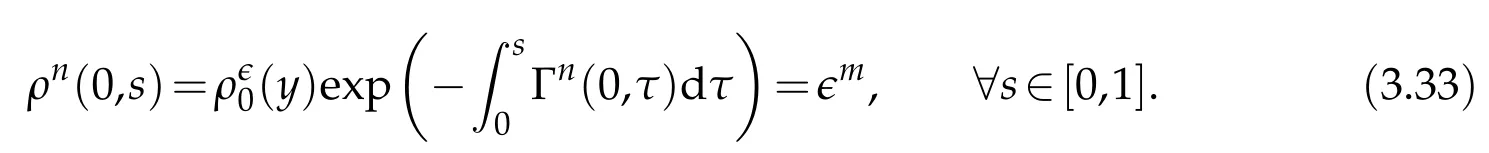
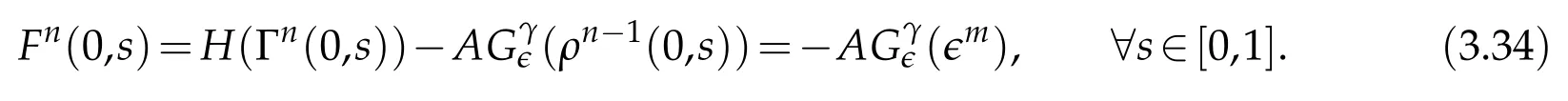


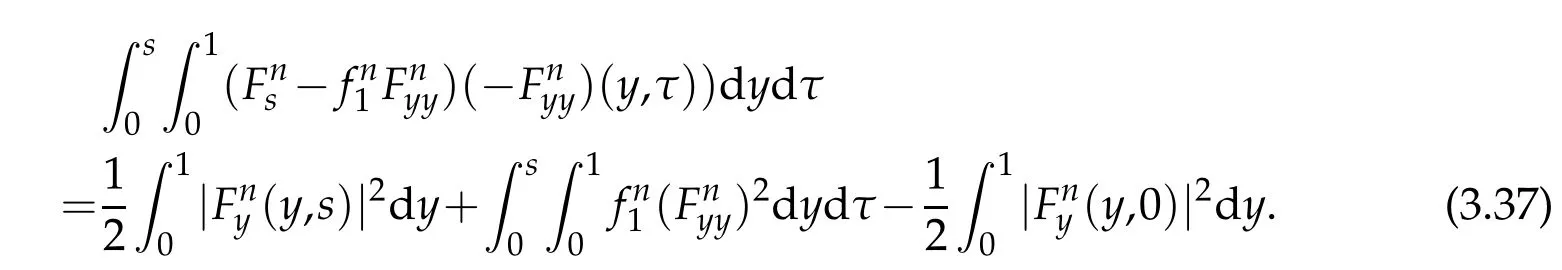
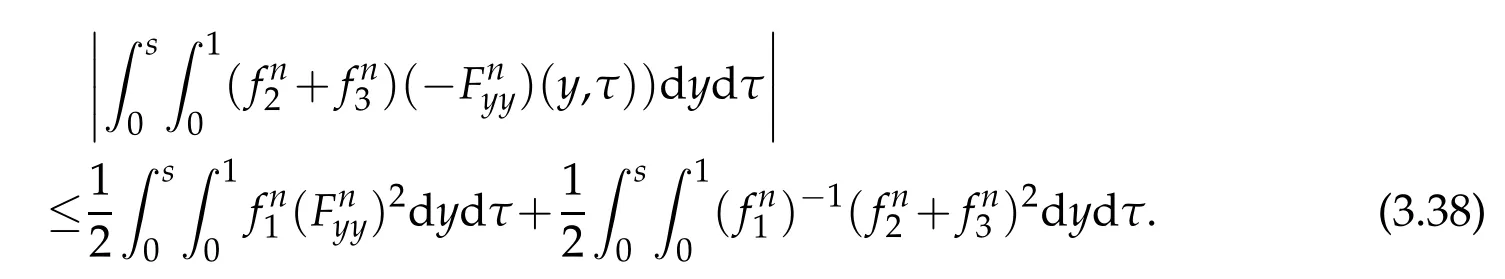
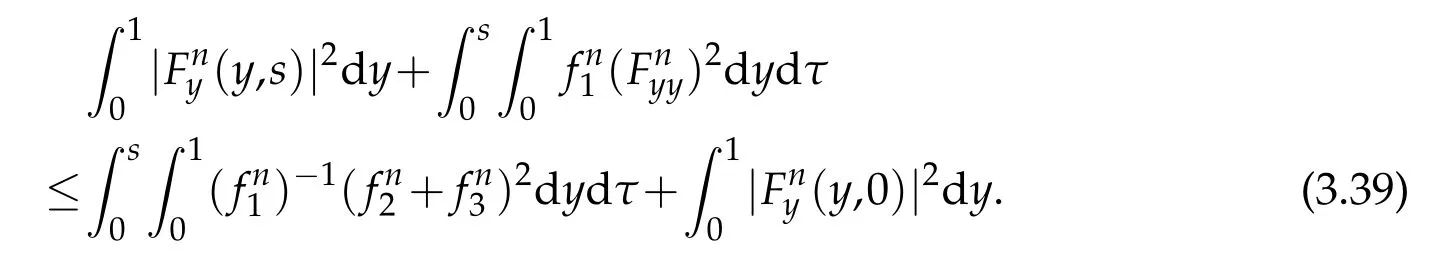
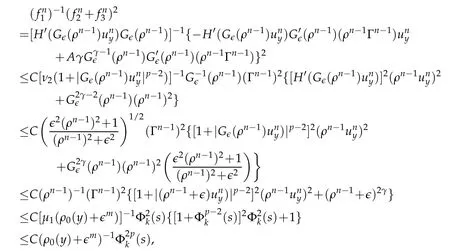
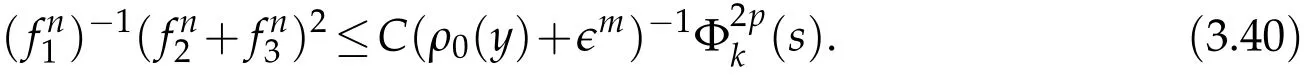

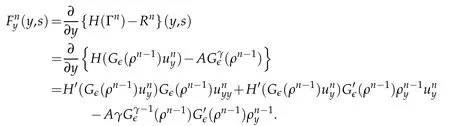
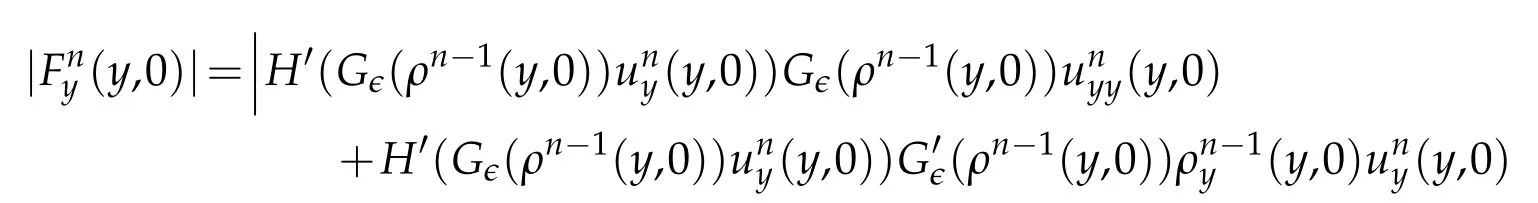
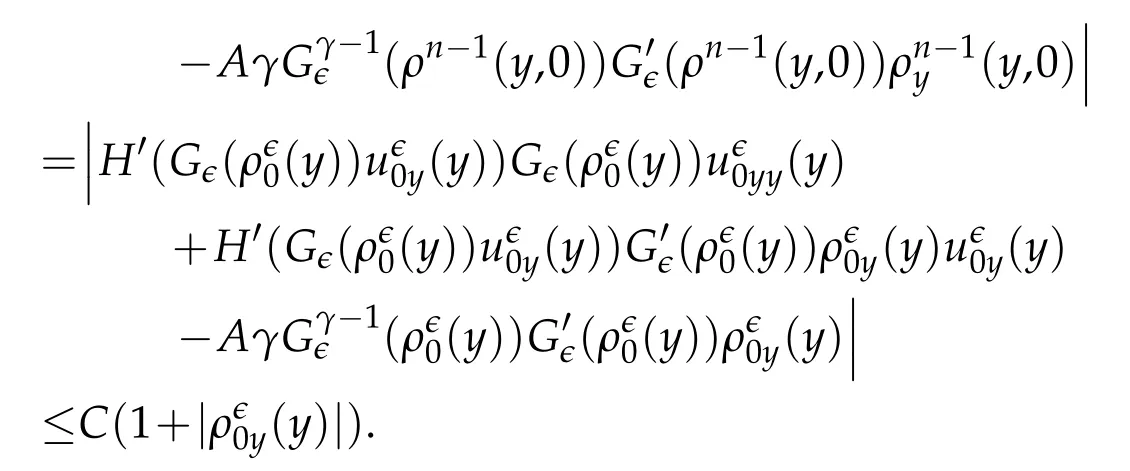

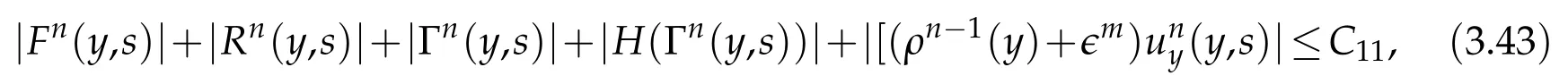
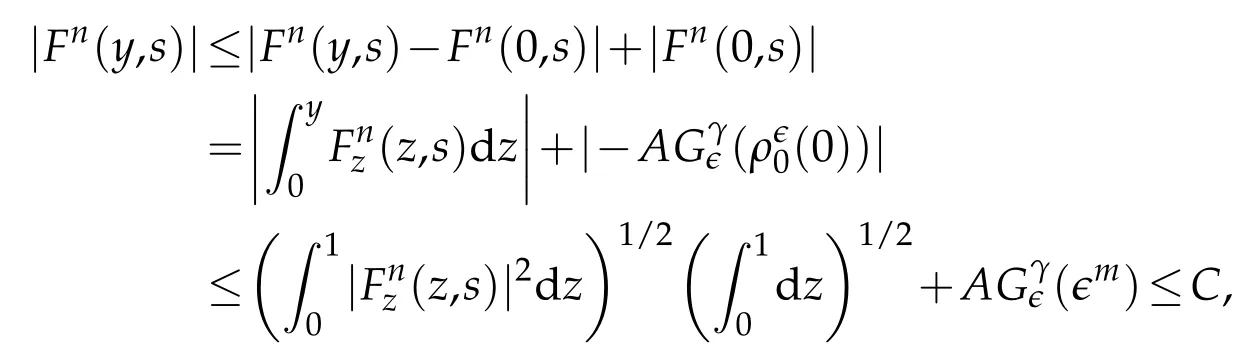

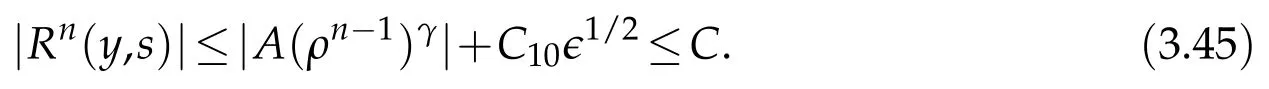
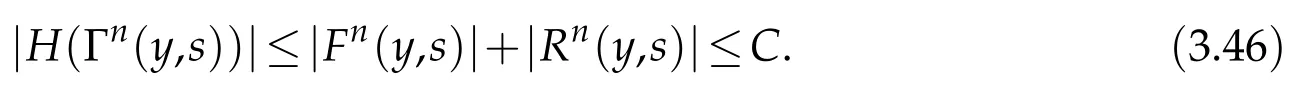

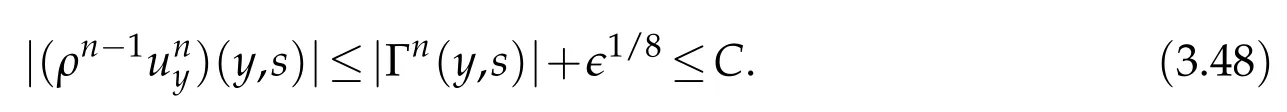
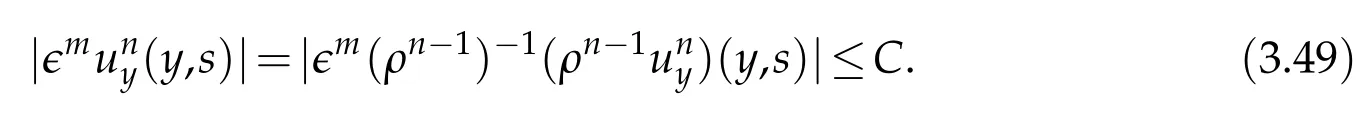
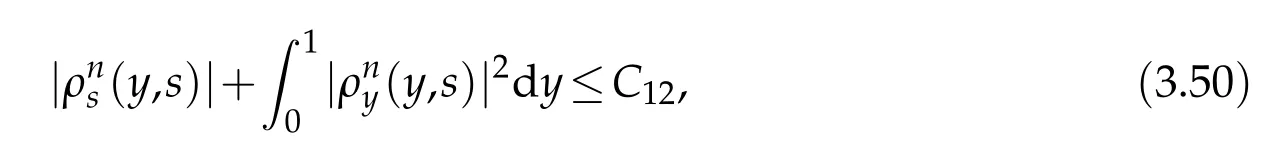

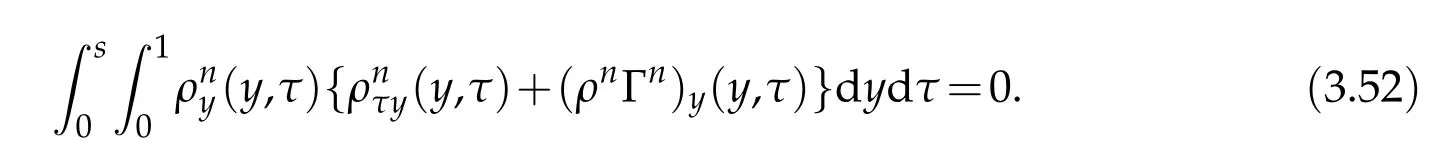
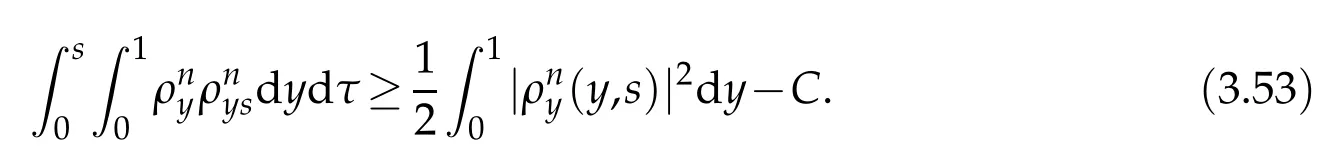
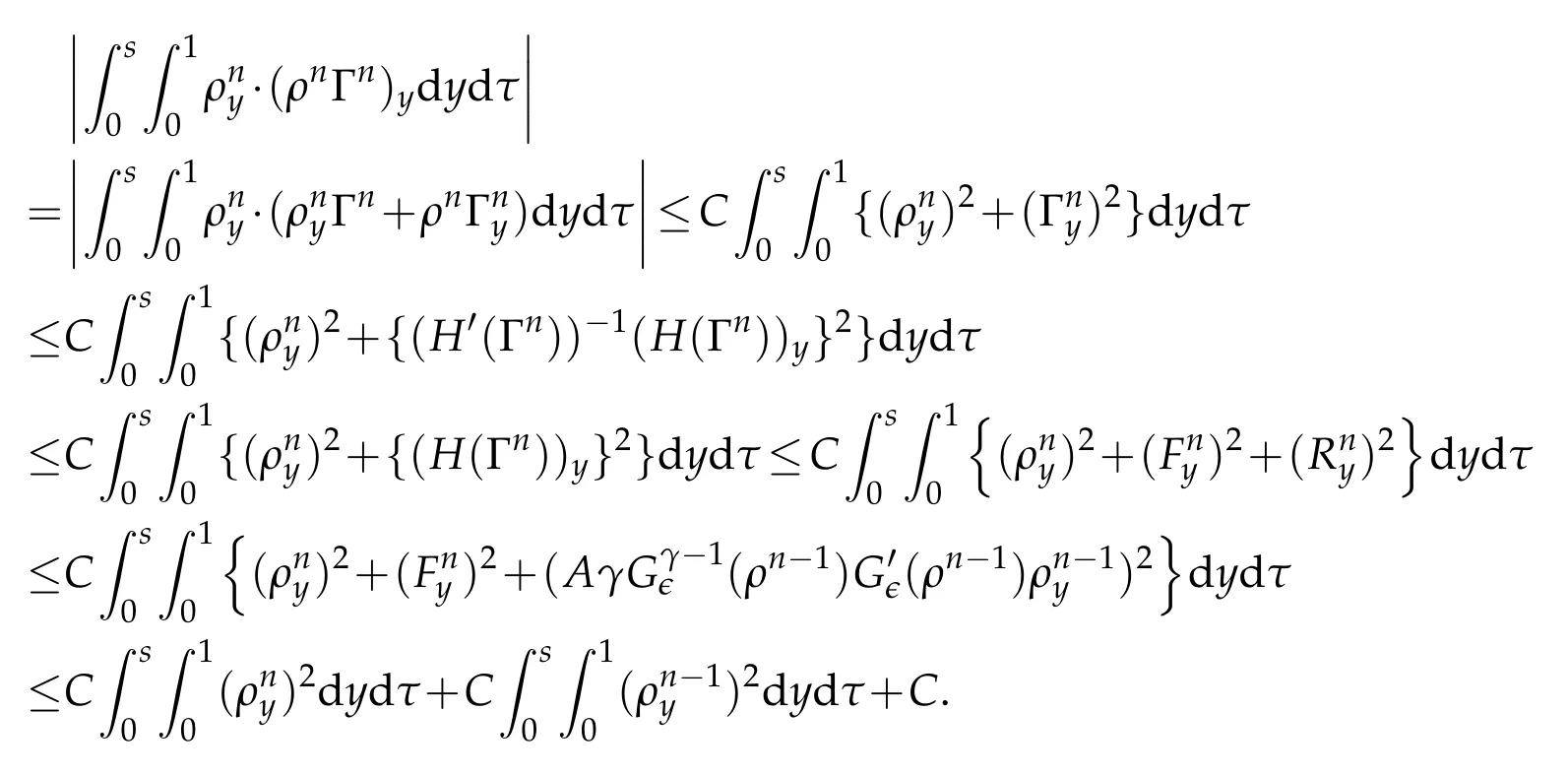
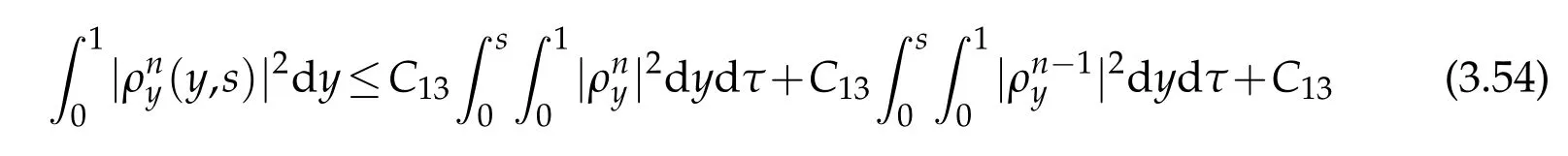
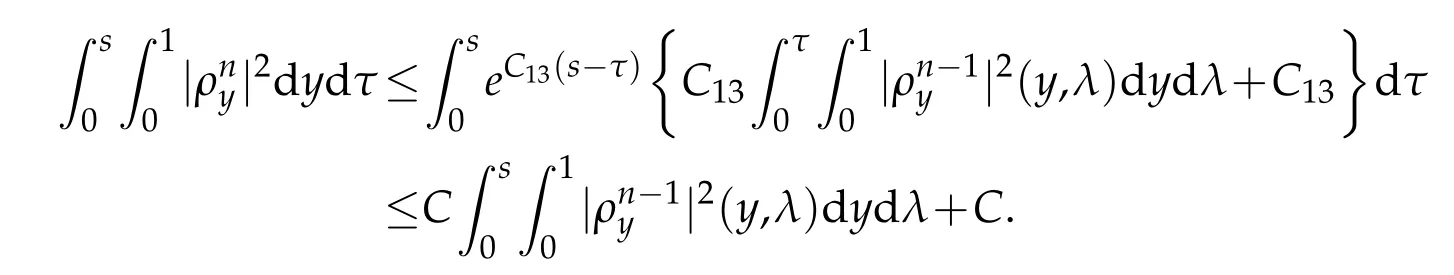
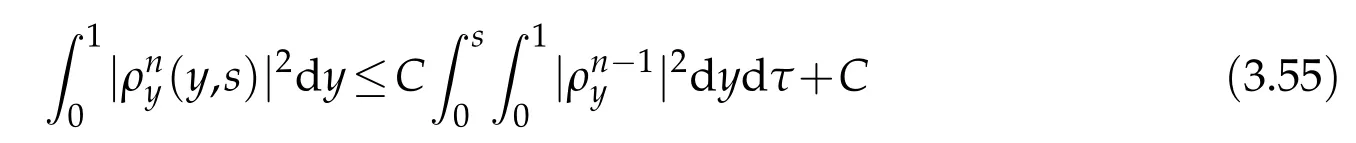
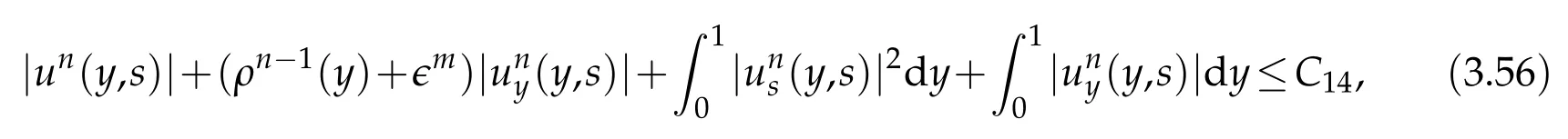
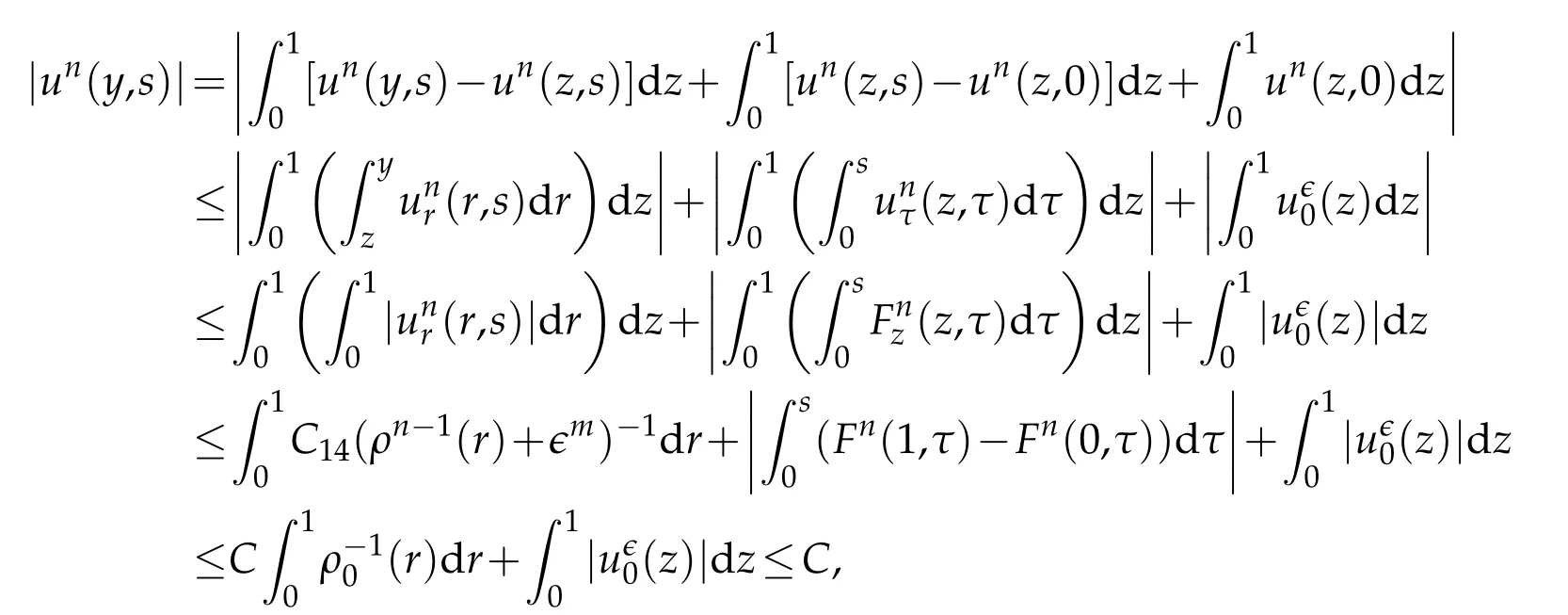


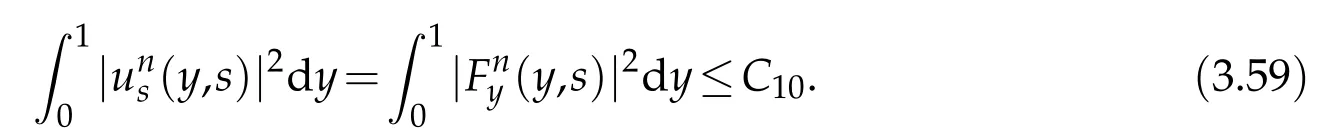
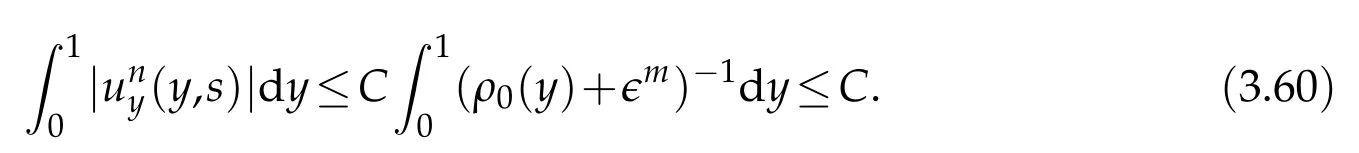

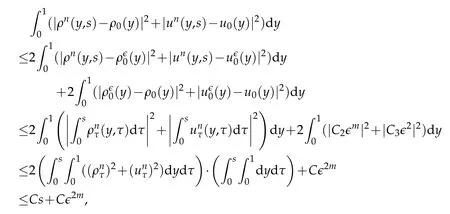
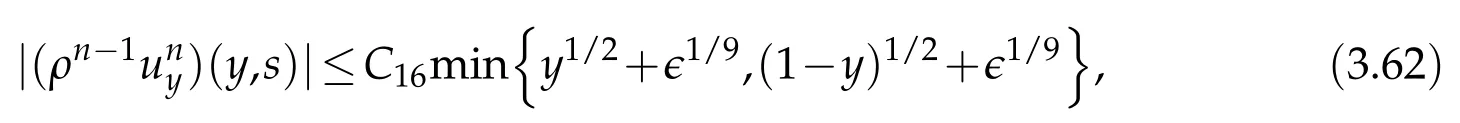
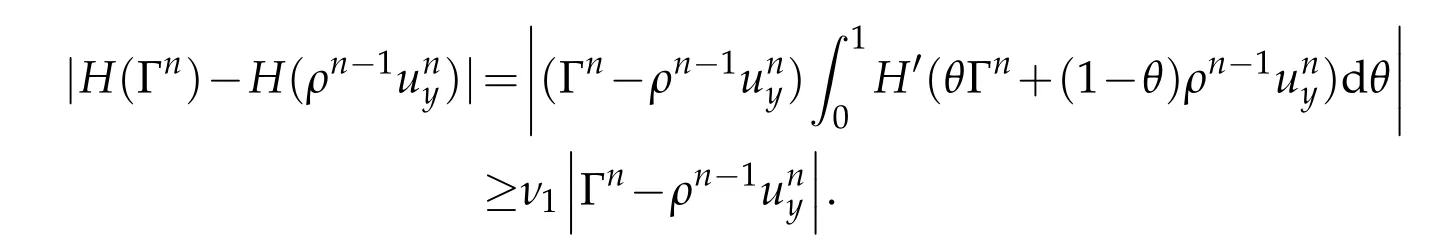

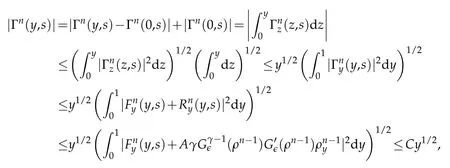

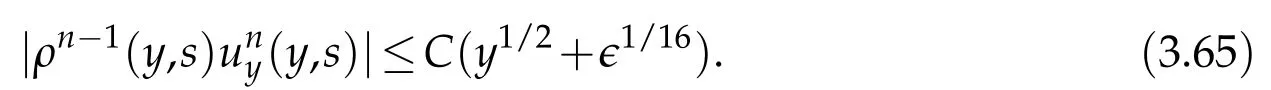
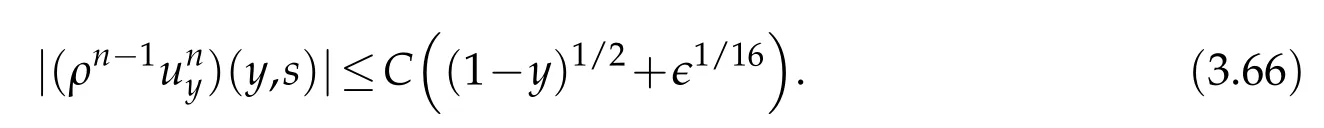
4 The proof of Theorem 1.1
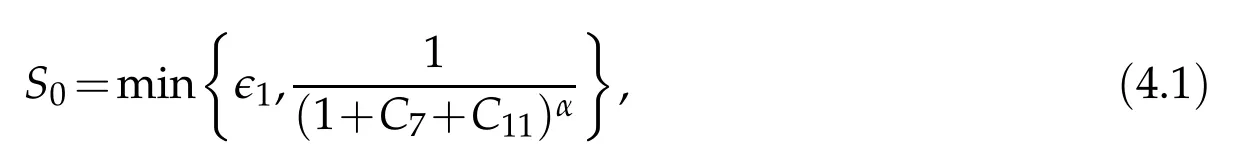

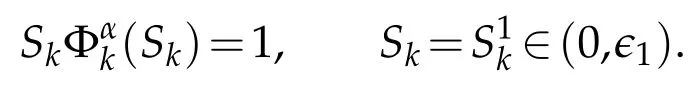
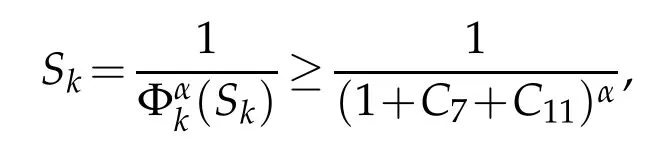
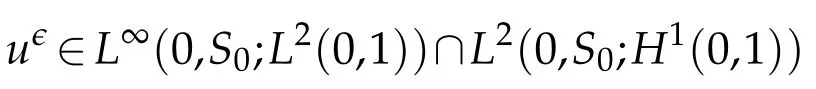


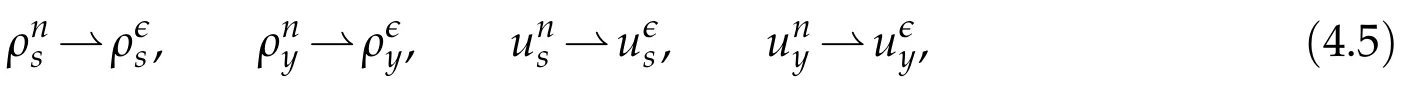

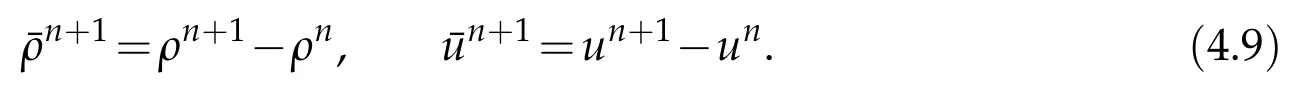


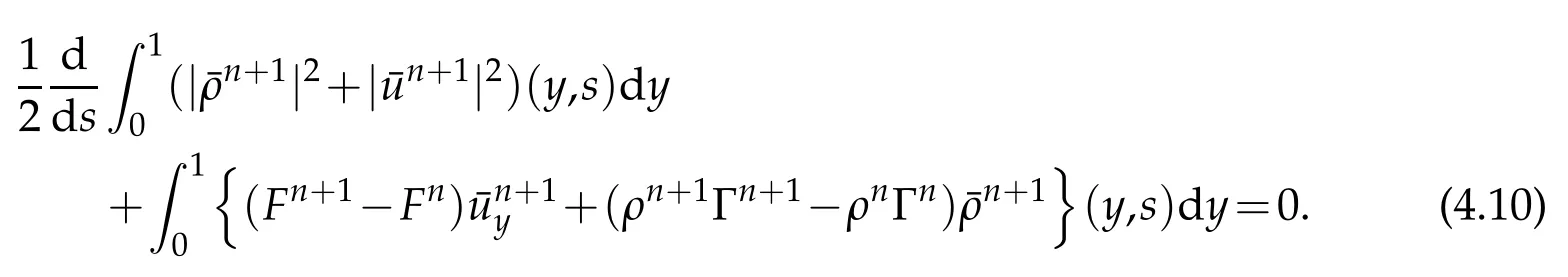
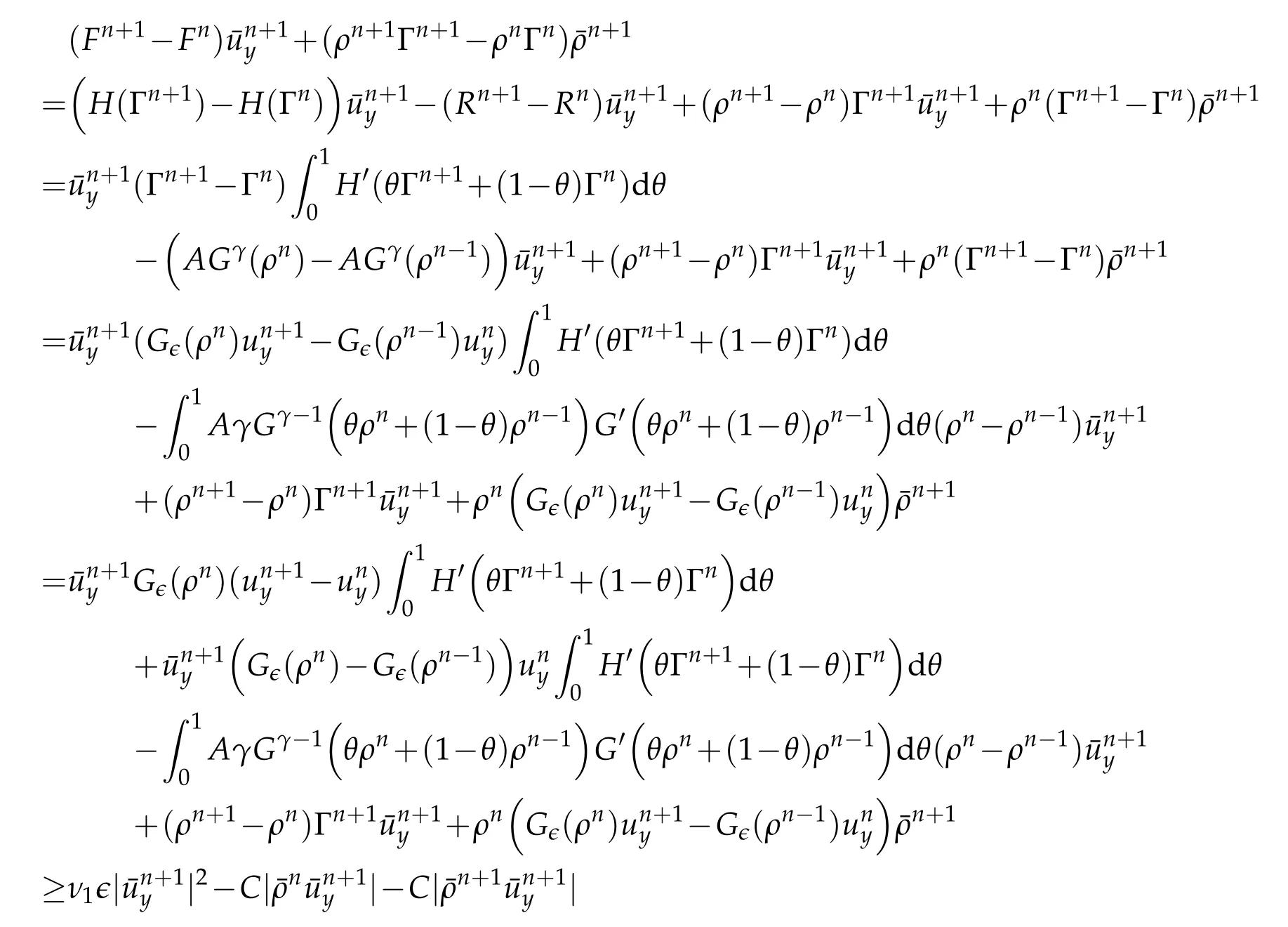

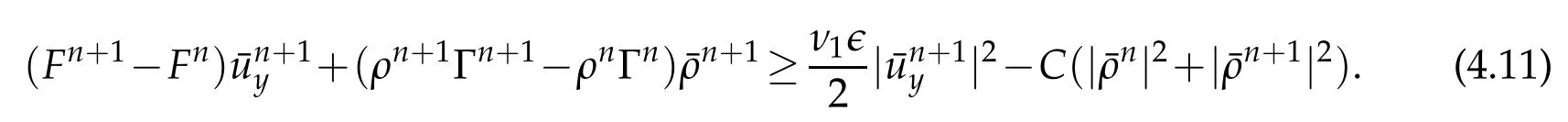
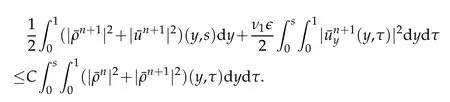

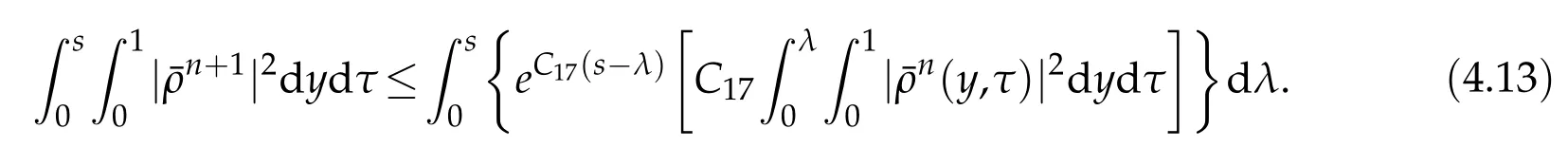
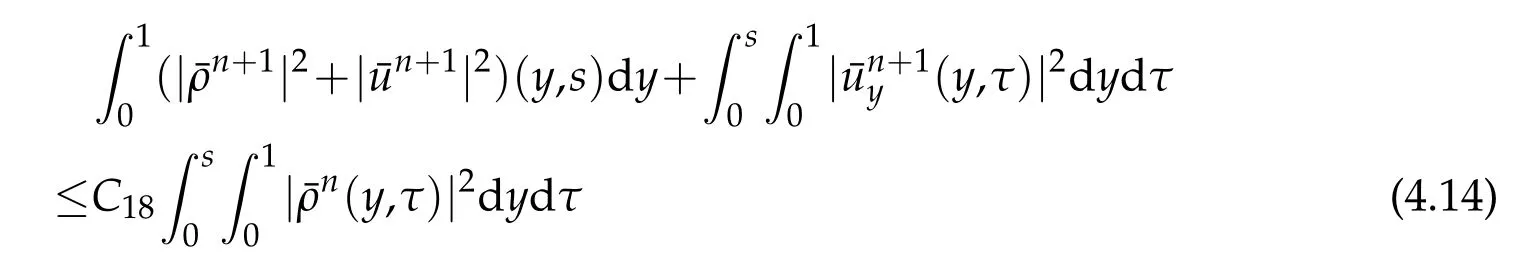
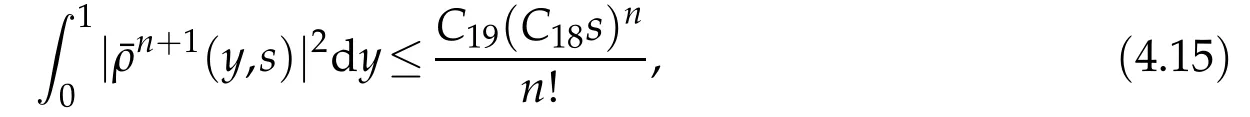
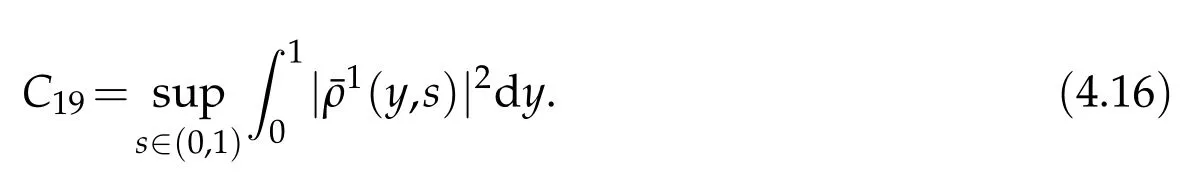
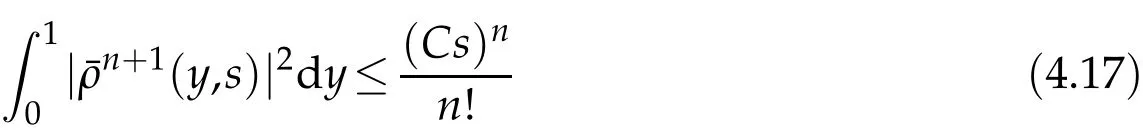

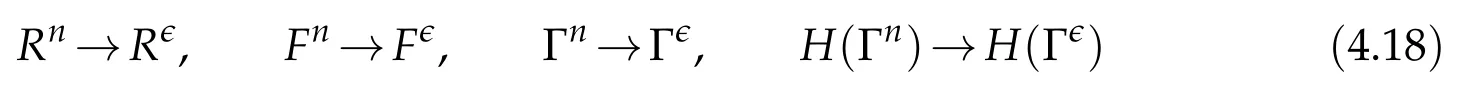
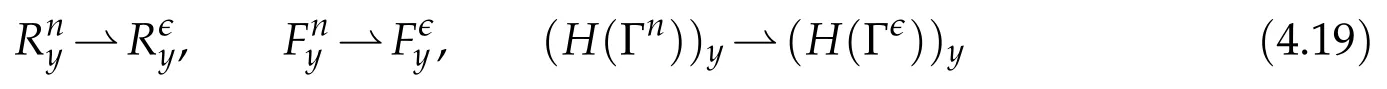
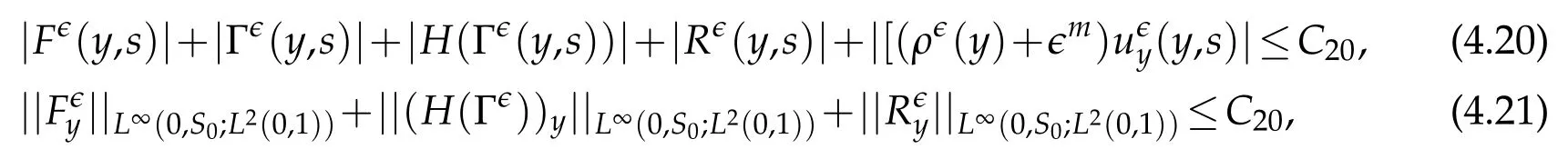
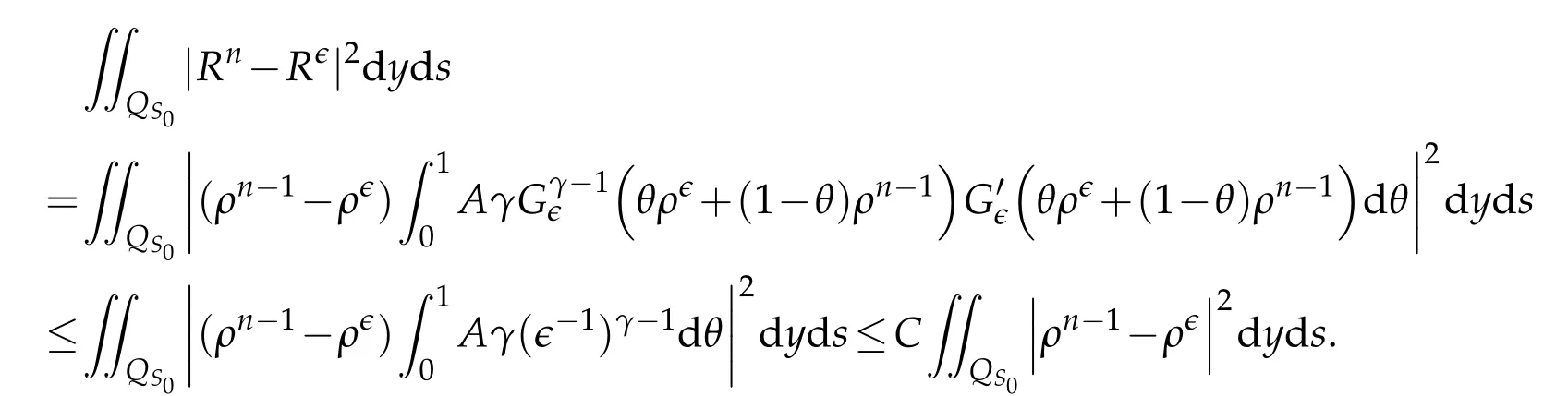

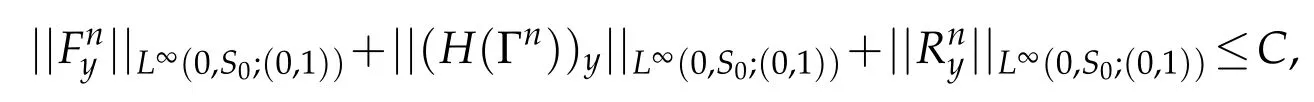

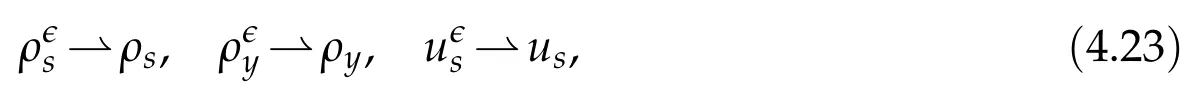

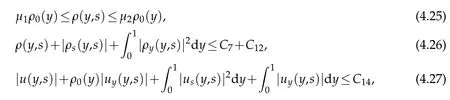





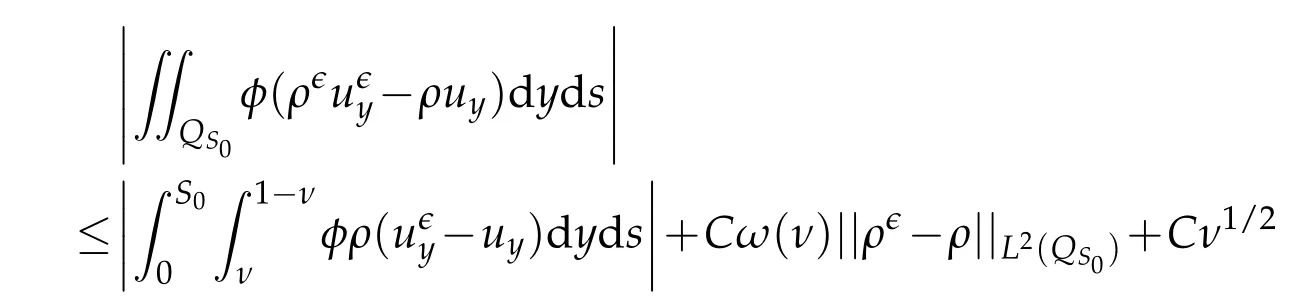


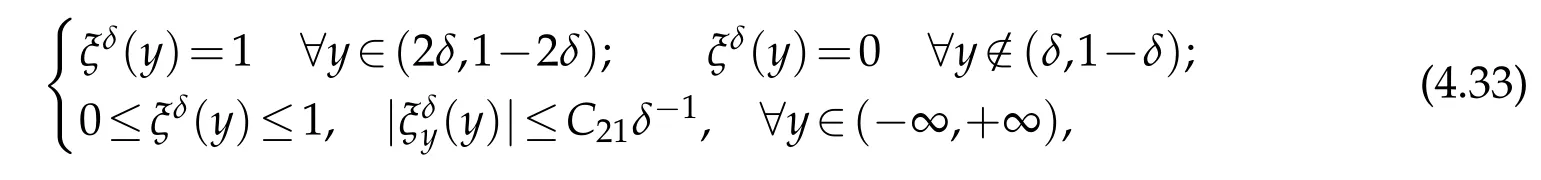

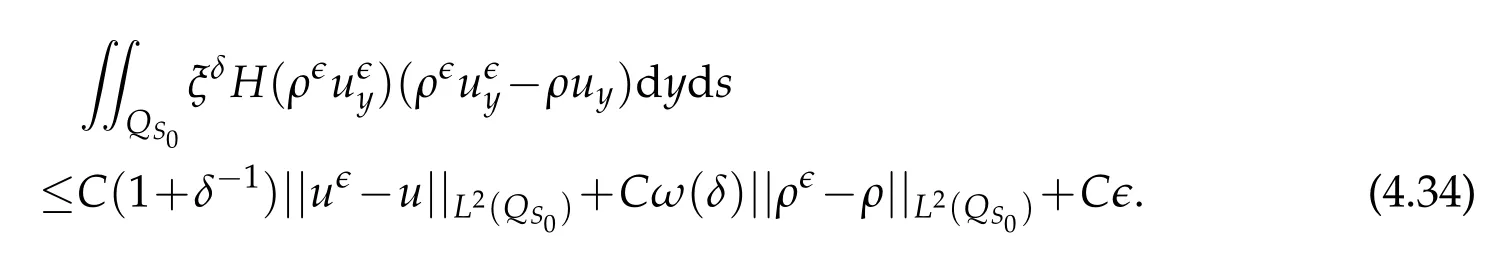

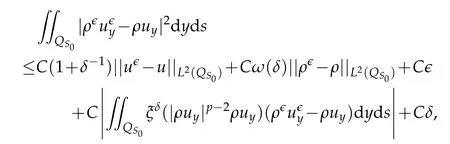

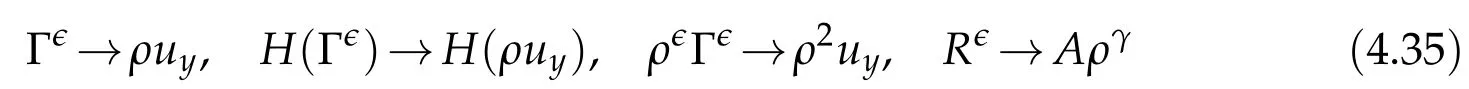
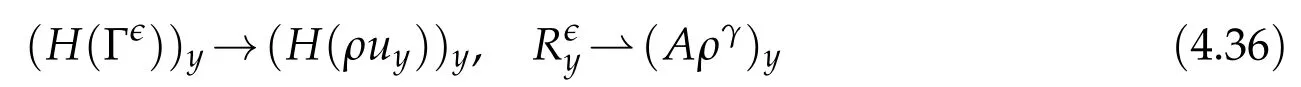
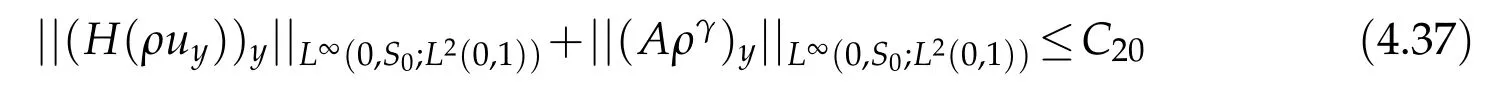
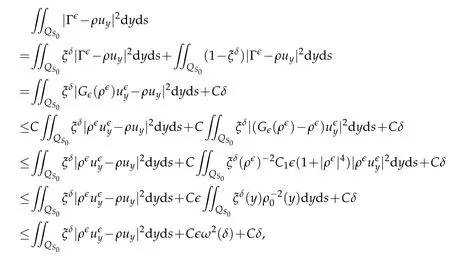
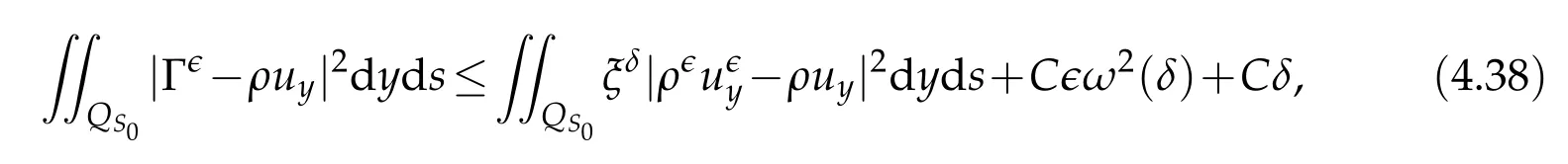
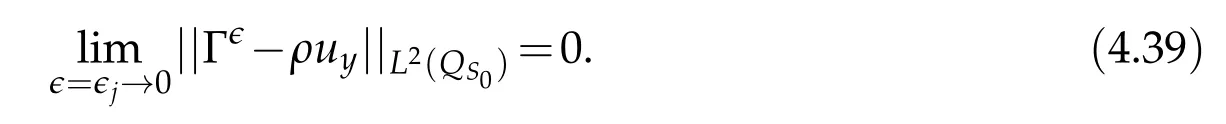
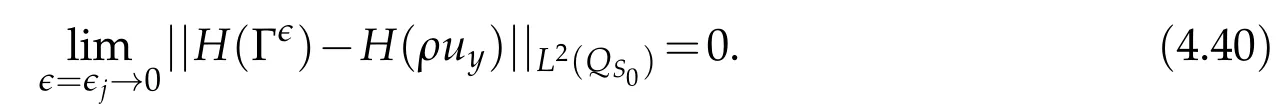
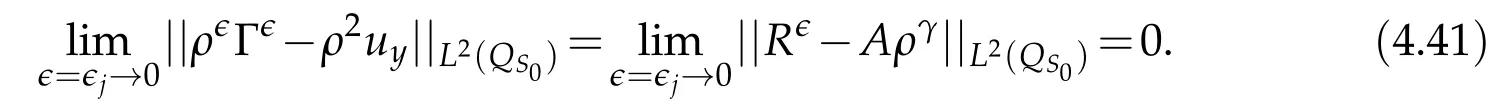
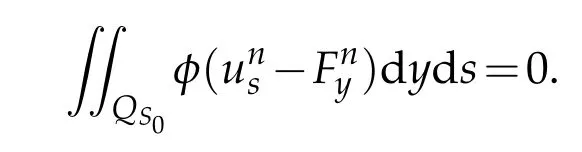
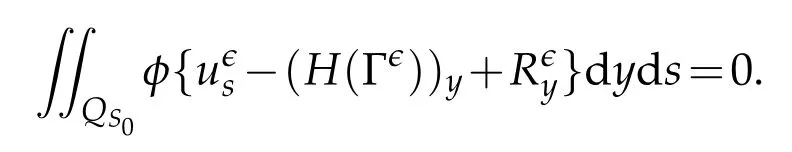
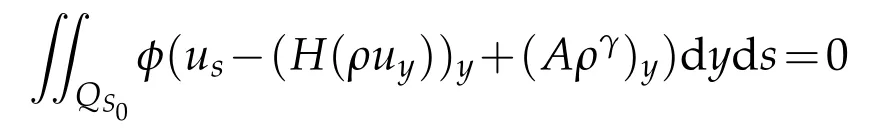

 Journal of Partial Differential Equations2021年1期
Journal of Partial Differential Equations2021年1期
