Zhibo Hou(侯志博), Qi Yin(殷琪), Chao Zhang(張超), Han-Sen Zhong(鐘翰森),Guo-Yong Xiang(項國勇),?, Chuan-Feng Li(李傳鋒), Guang-Can Guo(郭光燦),Geoff J.Pryde, and Anthony Laing

1Key Laboratory of Quantum Information,University of Science and Technology of China,CAS,Hefei 230026,China

2Synergetic Innovation Center of Quantum Information and Quantum Physics,University of Science and Technology of China,Hefei 230026,China

3Centre for Quantum Computation and Communication Technology(CQC2T)and Centre for Quantum Dynamics,Griffith University,Brisbane,4111,Australia

4Quantum Engineering and Technology Laboratories,School of Physics and Department of Electrical and Electronic Engineering,University of Bristol,UK

Keywords: teleportation,tomography,time reverse

1. Introduction

Methods for characterizing physical processes, found throughout science and engineering, naturally assume that a system must first exist before measurements can be performed for it.[1–3]However, the transfer of quantum information between particles does not need to follow a chronology that is expected in classical physics.[4]According to quantum mechanics, the state of a remote particle is instantaneously changed upon the measurement of a local particle with which it is entangled,[5]while teleportation protocols predict that a state can sometimes be received before it is sent.[6,7]A time symmetric picture of quantum mechanics explains these phenomena by viewing the act of a projective measurement as the preparation of a state that is sent backwards in time.[8–10]But because the results of quantum measurements are random in general,they cannot support superluminal communication or a communication channel with the past,so conflicts with fundamental principles such as special relatively are avoided. Any quantum state that is received before it is teleported will be mixed among a larger ensemble of transformed states from which it can be identified and sifted only at times after it is sent.[11]And the probability for an n-particle state to be faithfully received at a time before it is sent falls off exponentially.

These paradox-resolving clauses of time symmetry in quantum mechanics have consigned its application to intrinsically post-selected experiments of philosophical interest such as probabilistic simulations of closed time-like curves[4,7]or probabilistic demonstrations of nonlocality between particles before they interact via delayed choice experiments.[6,12–14]Here we experimentally demonstrate that time symmetry in quantum mechanics can be used to perform measurements for quantum systems ahead of time, in a way that is not possible in classical physics. Our protocol utilizes all received states,including transformed states, and unscrambles the classically recorded measurement results after the time of sending, to deterministically recover tomographic information.[15–18]Allowing state preparation to be performed after state measurement could open up new possibilities for characterization and verification[21–23]in engineered quantum systems[24]and in quantum physics more generally.[25]

2. Antedated tomography protocol

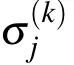
3. Experimental results

Fig.1. Schematic for antedated quantum tomography protocol and experimental implementation. (t0) A pair of qubits in the entangled state are encoded into the polarization of the two-photon state that is produced from pumping a pair of crossed non-linear crystals.(t1) Qubit B from the entangled pair is measured along a direction, which we implement at t =17 ns with a collection of waveplates, a polarizing beamsplitter (PBS), and two single photon detectors. Qubit A from this pair is stored in a quantum memory, realized here with a 31 m storage line between a series of 11 mirrors. (t2)Qubit 3 is initialized: a single nonlinear crystal is pumped to generate a pair of photons at t =105 ns, with one of the pair sent directly to a detector to herald the presence of the other. (t3) The state |ψ? is prepared on qubit 3 at t=130 ns with a series of waveplates. (t4)Qubit A is retrieved from the quantum memory and measured together with qubit 3 in the Bell basis,which we execute at t =132 ns with a PBS, a collection of waveplates, and four single photon detectors. The Bell measurement effectively sends the state τj|ψ?back through the quantum time channel to qubit B and on to the tomographic apparatus at t1. See Appendix for further experimental details.

Fig.2. Experimental results for antedated tomography. (a) With |D?≡|+? prepared at time t3 and sent at t4 by a Bell measurement with result λ0 or λ3,the ideal time channel to the tomography station at t1 is the identity or σz,respectively,so that|D?or|A?≡|??is measured,respectively. The real parts of the measured density matrices for both cases are displayed by solid colors with ideal values shown as the wire frame. (b)All six canonical polarization states were prepared so process matrices for the time channel could be reconstructed,the real parts of which are displayed. (c)The Bell measurement relies on Hong–Ou–Mandel interference between two photons generated at instants separated by 105 ns. The characteristic dip is shown for four-fold coincidence counts per 150 s,with a Gaussian fit(black line)to the experimental points and error bars calculated from Poisson statistics. (d)For each of the six prepared states, data was post-processed according to our antedated tomography protocol. Real parts of the reconstructed density matrices are respectively shown for prepared states|H?,|V?,|D?,and|A?;for|R?and|L?,the imaginary parts of the density matrices are shown in addition,below. See Appendix for numerical tables of density matrices and process matrices. ?

4. Discussion and conclusion

Much of the history of quantum science is the evolution of philosophically contentious concepts to practical applications.While causal order and time symmetry in quantum mechanics are fundamentally interesting,[9,33]removing the constraint of state-preparation before state-measurement could open up new avenues for existing characterization methods.[19,20]If entangling measurements between different types of particles,such as atomic and molecular ions,[34]become feasible, then a tomographic capability that is more readily available at an earlier time or for a certain atomic species,[35]can be deployed to characterize states encoded in less accessible physical systems at later times. In solid state quantum processors,[36]tomography could be performed ahead of time using photons for subsequently prepared states of spins,or for the mediating electronic spin, with the long lived nuclear spin serving as a quantum memory. Because the general antedated quantum tomography protocol is deterministic, it could prove useful for characterizing or verifying larger physical systems that are efficiently described by matrix product states.[37]

Appendix A

Entangled state generationPulses from a mode-locked Ti-sapphire laser with a duration of 140 fs, a repetition rate of 76 MHz, and a central wavelength of 780 nm first passed through a frequency doubler. The resultant ultraviolet pulses with a power of 200 mW then(at t =0 ns)pumped a pair of sandwiched beam-like-type cut BBO crystals, each of thickness 1 mm,to produce a stream of photon pairs,entangled in their polarization. Temporal and spatial compensation (TSC)was made with LiNbO3and YVO4crystals.[38]The photonic qubits were then distributed to Alice and Bob via a pair of 3 m single mode fibres (SMF). Half waveplates (HWP) and tilted quarter waveplates(QWP)at both ports of the fibres were used to maintain the polarization reference frame.

With the photonic qubits on Alice’s side having passed through the 31 m delay line and a 2 m SMF,both qubits were measured in the Pauli basis (details below), and their density matrix was reconstructed by the maximum likelihood estimation algorithm.[15]The quantum state that generates the experimental data with the highest probability is which has a fidelity of 0.927±0.001 with the ideal state,where the error is the standard deviation from 100 numerical simulations with Poissonian statistics.

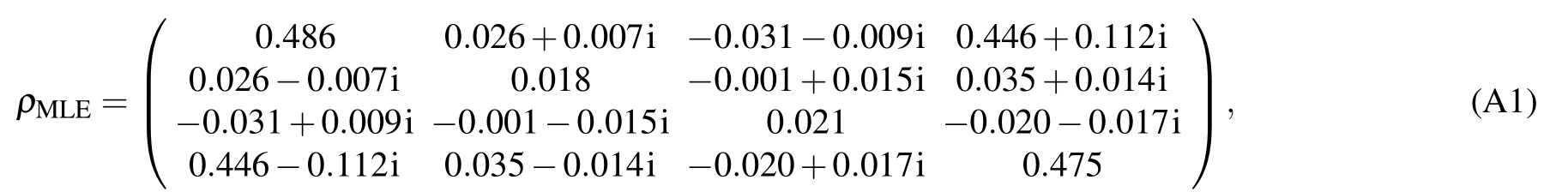
Tomographic setup for photon BFrom each pair, the photon on Bob’s side,photon B,was immediately injected into its tomographic set up and measured at t =17 ns, due to the overall optical path length from photon generation, including the approx. 0.6 m in this section. The module contained a HWP,a QWP,a polarization beam splitter(PBS),and a single photon detector(SPD),to realize arbitrary projective measurements on qubits encoded in the polarization of photons. This photon finally passed through an interference filter(FWHM of 8 nm)before detection. Waveplate settings were chosen to implement measurements in the three Pauli bases,and the results were stored with respect to these settings.

Delay line for photon AThe photon on Alice’s side,photon A, was directed to a delay line, comprised of eleven mirrors which reflected the photon through 31 m of free-space before coupling to 2 m of SMF.A telescope was implemented with three concave lenses,resulting in an overall collection efficiency of approx. 50% including losses from reflection and fibre insertion.

Generation and sate preparation for photon 3After 8 consecutive pump pulses (105 ns), a second beam-like BBO crystal was pumped to generate pairs of (unentangled) photons, with one photon from each pair directly detected as a trigger, after passing through an interference filter (FWHM of 8 nm). The other photon from this pair, photon 3, passed through a 5 m SMF, after which its state was prepared by a combination of HWP and QWP.

Table A1. Reconstructed single qubit density matrices andfor all six states |φ3? prepared on photon 3, alongside their corresponding fidelities with errors.

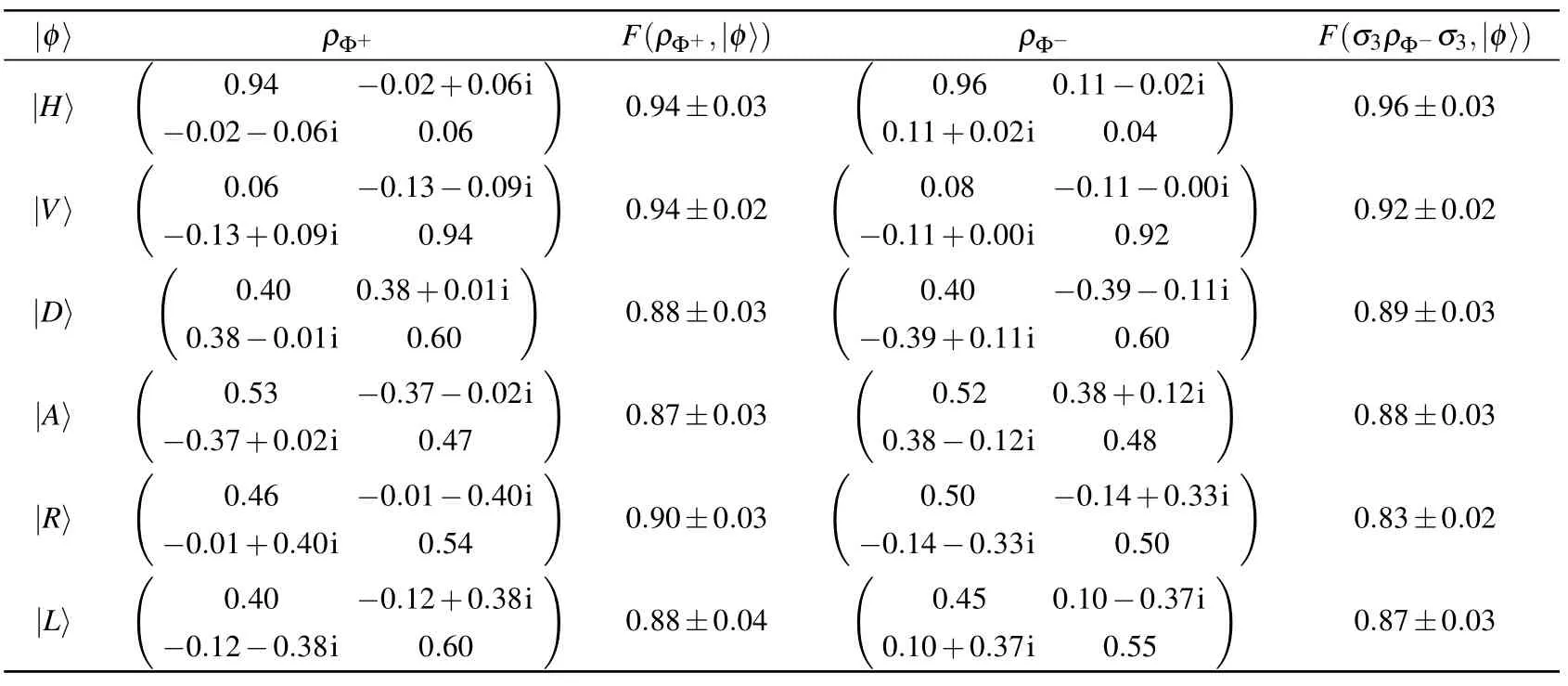
Table A1. Reconstructed single qubit density matrices andfor all six states |φ3? prepared on photon 3, alongside their corresponding fidelities with errors.

?

Table A2. Reconstructed single qubit density matrices ρ3 for all six states |φ3? prepared on photon 3, alongside their corresponding fidelities with errors.

The S±m(xù)atrices are simply transformed into χ±from the standard definition[40]

with identity and Pauli operators σm,such that

with

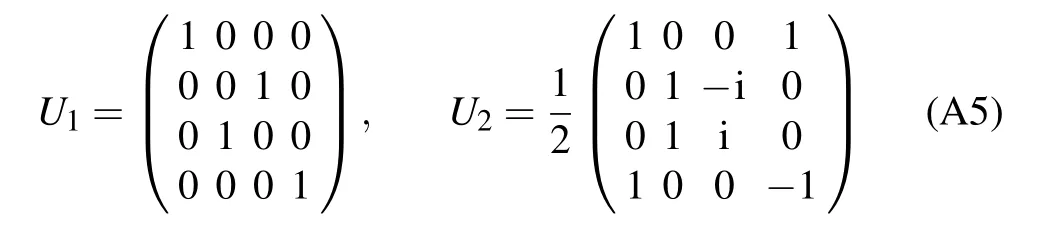
to give

The process fidelities are immediately available in this representation as 0.84±0.02 and 0.83±0.02 for the identity and σ3, respectively where the errors on the fidelities are the standard deviations from 100 simulated results with Poissonian statistics.

Acknowledgement

We are grateful to S.Popescu and T.Short for helpful discussions.