遲曉妮,張睿婕,劉三陽(yáng)

(1.桂林電子科技大學(xué)數(shù)學(xué)與計(jì)算科學(xué)學(xué)院,廣西 桂林541004;2.桂林電子科技大學(xué)廣西密碼學(xué)與信息安全重點(diǎn)實(shí)驗(yàn)室,廣西 桂林541004;3.桂林電子科技大學(xué)廣西自動(dòng)檢測(cè)技術(shù)與儀器重點(diǎn)實(shí)驗(yàn)室,廣西 桂林541004;4.西安電子科技大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,陜西 西安710071)

1.引言

作為互補(bǔ)問(wèn)題[1]的推廣,權(quán)互補(bǔ)問(wèn)題[2]在科學(xué)和工程等領(lǐng)域有著廣泛的應(yīng)用.Potra[2]證明了Fisher市場(chǎng)均衡問(wèn)題可以建模為非線性互補(bǔ)問(wèn)題[3],也可以建模為權(quán)互補(bǔ)問(wèn)題,但后者在某些情況下能得到更高效的數(shù)值解方法[4].全牛頓步內(nèi)點(diǎn)算法[5]是求解線性規(guī)劃的熱門算法.2003年,Darvay[6]基于連續(xù)可微函數(shù)提出求解線性規(guī)劃的新全內(nèi)點(diǎn)算法,并給出了該算法的迭代復(fù)雜度.隨后,Darvay[7]等人又提出求解線性規(guī)劃的新全牛頓步內(nèi)點(diǎn)算法,并分析了算法的多項(xiàng)式迭代復(fù)雜度.由于權(quán)向量非零,權(quán)互補(bǔ)問(wèn)題的理論[8]和算法研究相比于互補(bǔ)問(wèn)題更為復(fù)雜,因此關(guān)于權(quán)互補(bǔ)問(wèn)題的算法尚不多見(jiàn).Potra[9]設(shè)計(jì)了一種預(yù)估-校正內(nèi)點(diǎn)算法[10]用于求解充分權(quán)互補(bǔ)問(wèn)題.

本文將文[11]中P?(κ)線性互補(bǔ)問(wèn)題全牛頓步可行內(nèi)點(diǎn)算法的連續(xù)可微函數(shù)推廣到權(quán)互補(bǔ)問(wèn)題,對(duì)中心路徑進(jìn)行等價(jià)變換得到新搜索方向,給出求解Rn上線性權(quán)互補(bǔ)問(wèn)題的可行內(nèi)點(diǎn)算法.該算法采用全牛頓步,避免進(jìn)行線搜索求解步長(zhǎng),節(jié)省了計(jì)算時(shí)間和內(nèi)存.分析了算法的可行性,并證明其迭代復(fù)雜度與目前線性優(yōu)化最好的多項(xiàng)式時(shí)間復(fù)雜度相同.數(shù)值算例結(jié)果表明算法的有效性.

2.算法

考慮Rn上的線性權(quán)互補(bǔ)問(wèn)題(LWCP)[1]：尋找向量對(duì)(x,y,s)∈Rn×Rm×Rn使得

其中A ∈Rm×n,b ∈Rm,c ∈Rn,ω ∈Rn++.定義LWCP(2.1)的嚴(yán)格可行域?yàn)閩

令初始點(diǎn)(x0,y0,s0)∈F0,ω(t)=tx0s0+(1?t)ω,其中t ∈[0,1] 且t0=1.考慮(2.1)的擾動(dòng)問(wèn)題

這里e=(1,··· ,1)T.假定A為行滿秩矩陣,即R(A)=m.若內(nèi)點(diǎn)條件(IPC)[5]成立,即(x,y,s)∈F0,則對(duì)任意參數(shù)t ∈(0,t0],方程組(2,2)有唯一解(x(t),y(t),s(t)).集合{(x(t),y(t),s(t))|t>0}稱為L(zhǎng)WCP(2.1)的中心路徑.當(dāng)t →0時(shí)ω(t)→ω,得LWCP(2.1)的最優(yōu)解.

考慮線性優(yōu)化問(wèn)題內(nèi)點(diǎn)算法中的連續(xù)可微函數(shù)[6]φ:R+→R+,并假設(shè)其反函數(shù)φ?1存在.用等價(jià)變換替換LWCP的擾動(dòng)問(wèn)題(2.2)中第三式,則新牛頓搜索方向(?x,?y,?s)應(yīng)滿足方程組

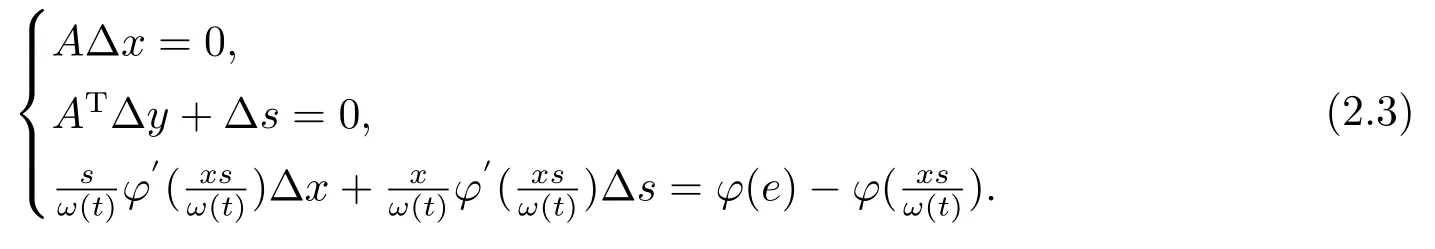
定義

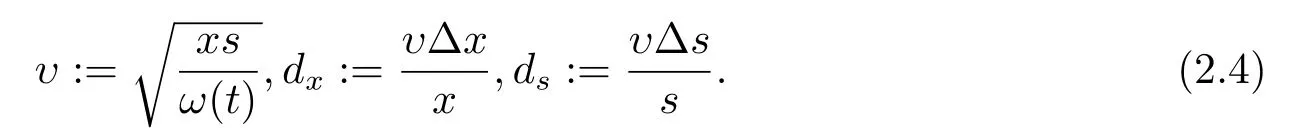
由(2.4)式可知,方程組(2.3)可化為

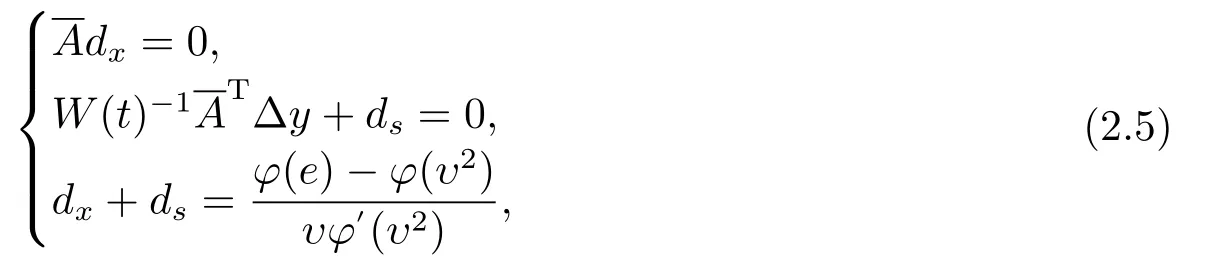
其中:=AV ?1X,V:=diag(υ),X:=diag(x),W(t)=diag(ω(t)).

將P?(κ)線性互補(bǔ)問(wèn)題的全牛頓步可行內(nèi)點(diǎn)算法中的函數(shù)[11]推廣到LWCP(2.1),則方程組(2.5)可化為

定義鄰近測(cè)度

令

引理2.1[5]若u與v正交,則

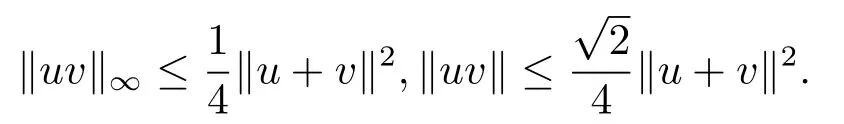
由方程組(2.6)知dTx ds=0.因此由(2.8)式得

由引理2.1和(2.7)式可知

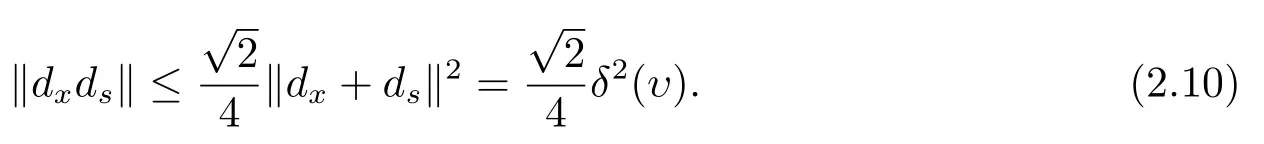
引理2.2對(duì)任意υ ∈Rn,有

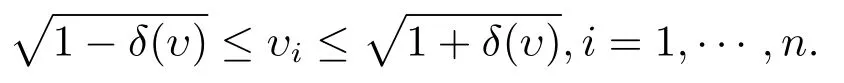
選取適當(dāng)參數(shù)θ及任意初始點(diǎn)x0>0,s0>0,y0= 0,令ω(t0)=x0s0,其中t0= 1.顯然δ(x0,s0,ω(t0))=0.求解方程組(2.6)并結(jié)合(2.4)式得牛頓搜索方向(?x,?s,?y),其中t+=(1?θ)t,θ ∈(0,1).令新迭代點(diǎn)

滿足內(nèi)點(diǎn)條件并且δ(x+,s+;ω(t+))<βt+.當(dāng)∥xs ?ω∥≤ε時(shí),算法終止.下面給出本文算法的具體步驟.

算法2.1求解LWCP的新全牛頓步可行內(nèi)點(diǎn)算法

步1 選擇參數(shù)t0= 1,ε >0,β ∈(0,1),初始點(diǎn)(x0,y0,s0)∈F0,y0= 0且ω(t0)=x0s0.置k:=0.

步2 當(dāng)∥xs ?ω∥≤ε,算法終止;否則轉(zhuǎn)步3.

步3 求解方程組(2.6)并結(jié)合(2.4)式得搜索方向(?x,?s,?y),令

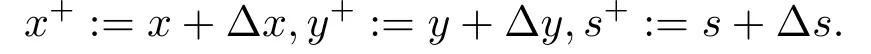
步4 由下面的(4.1)式求得θ ∈(0,1),令

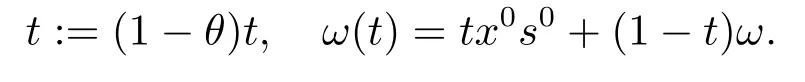
置k:=k+1.轉(zhuǎn)步2.

3.算法分析

引理3.1若δ(υ)<1,則(x+,y+,s+)∈F0.

證令α ∈[0,1],記

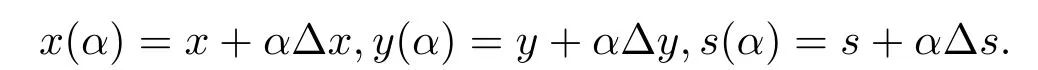
由(2.4),(2.8)式和方程組(2.6)得

因?yàn)棣?t)>0,(1?α)υ2≥0,所以由(3.1)式知,若

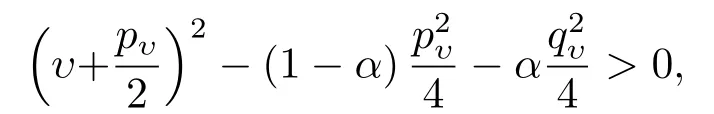
則x(α)s(α)>0.由(2.7)和(2.9)式,及δ(υ)<1可知

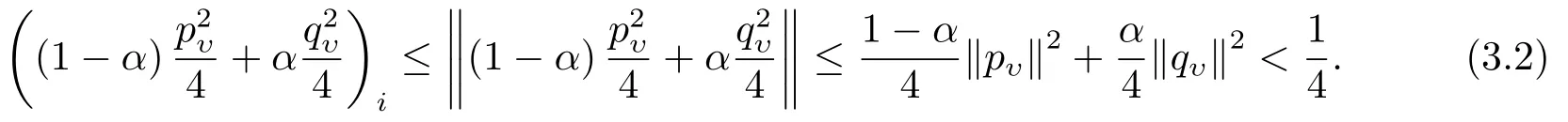
又由(2.7)式和引理2.2得

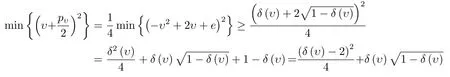
當(dāng)δ(υ)<1時(shí),由(3.3)式得

因此若δ(υ)<1時(shí),則由(3.1),(3.2)和(3.4)式可得x(α)s(α)>0.

由于x(0)=x>0,s(0)=s>0且x(α),s(α)與α呈線性關(guān)系,所以對(duì)α ∈[0,1]有x(α),s(α)>0,相應(yīng)地,x(1),s(1)>0.證畢.

引理3.2令,則

證由(3.1)式和引理2.2得

令f(η)=η2+η ?η3.由f′(η)=2η+1?3η2=?(3η+1)(η?1)知,f(η)在(0,1)為單調(diào)遞增函數(shù).故由f(η)≤f(1)=1,η ∈(0,1)可得

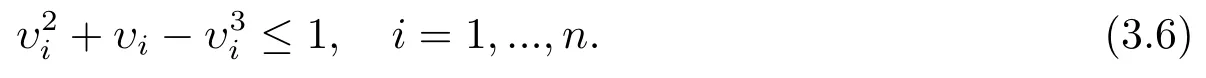
因此,由(2.10),(3.5)和(3.6)式,得

引理3.3令若δ(υ)<1,則

證由(2.6),(2.8)和(3.1)式得

因?yàn)棣?υ)<1,所以由引理2.2可得

由(2.7),(2.8),(2.9),(3.7)和(3.8)式知,當(dāng)δ(υ)<1時(shí)有

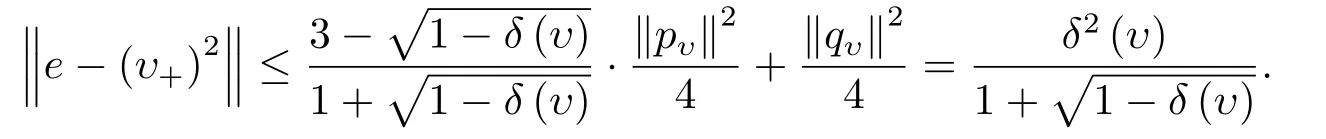
引理3.4令,則

證因?yàn)棣?t+)=ω(t)+θt(ω ?x0s0),所以

故由引理3.3得

引理3.5令則

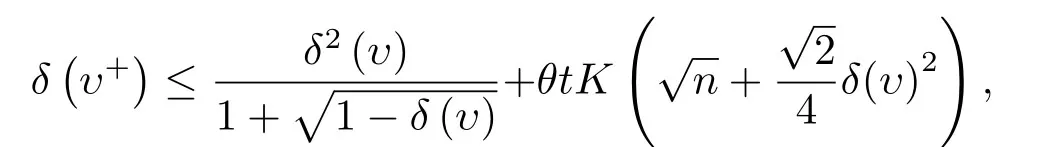
證由引理3.2和引理3.4得

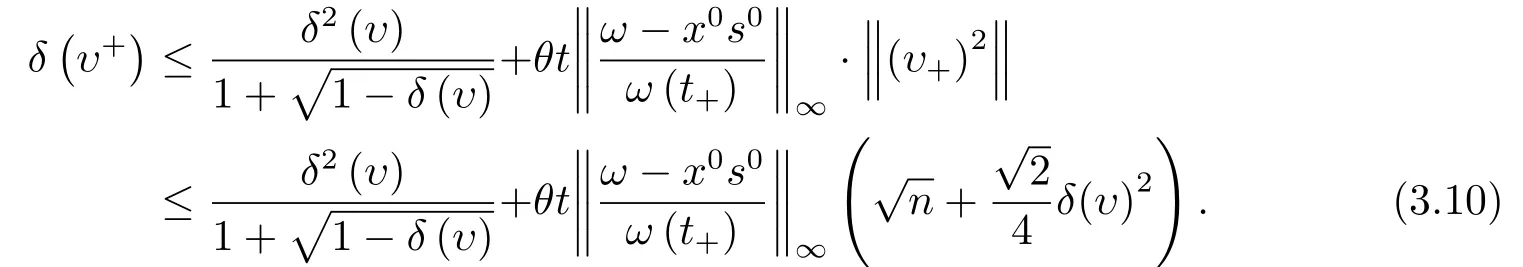
引理3.6給定常數(shù)β ∈(0,1),令若δ(υ)≤βt,則δ(υ+)<βt+.

證由引理3.5得

因?yàn)?3.11)式右端函數(shù)關(guān)于δ(υ)單調(diào)增加,所以若δ(υ)≤βt,則

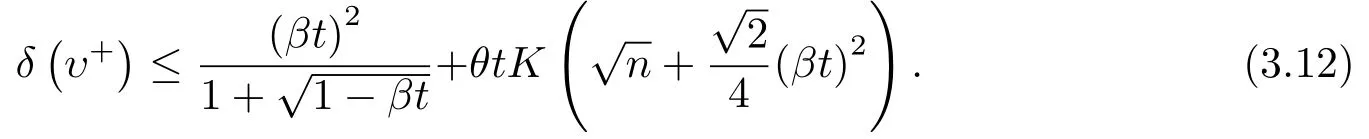
不妨設(shè)

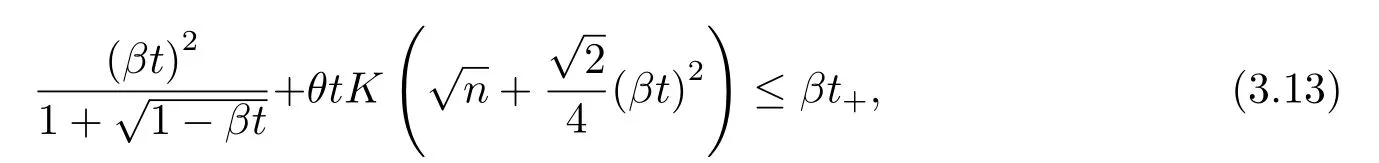
其中t+=(1?θ)t,θ ∈(0,1)化簡(jiǎn)(3.13)式得

即

因?yàn)棣?∈(0,1),所以故由式(3.14)得

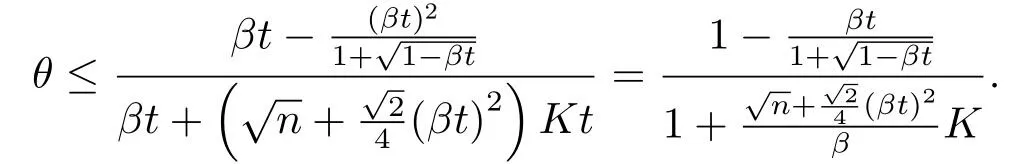
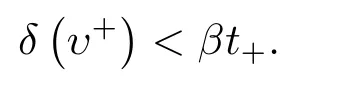
4.復(fù)雜度分析

選取參數(shù)β ∈(0,1),t ∈[0,1],令

因?yàn)閠0= 1,則ω(t0)=x0s0,故δ(υ0)= 0<βt0.又t+= (1?θ)t,由引理3.1和引理3.6可知下一迭代點(diǎn)(x+,y+,s+)嚴(yán)格可行且δ(υ+)<βt+.

引理4.1設(shè)參數(shù)θ,K按(4.1)式選取.若δ(υ)≤βt,則

證由引理3.3得

因?yàn)棣?∈(0,1),t ∈[0,1]所以若δ(υ)≤βt,則

引理4.2設(shè)參數(shù)θ,K按(4.1)式選取.若LWCP(2.1)存在最優(yōu)解,則算法2.1至多經(jīng)過(guò)

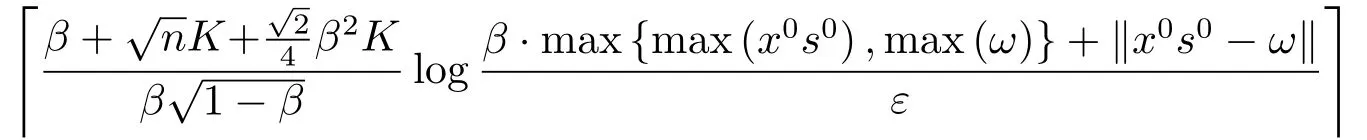
次迭代得到LWCP(2.1)的ε-近似解.

證因?yàn)椤桅?t)∥∞≤max{max(x0s0),max(ω)},所以由引理4.1可得

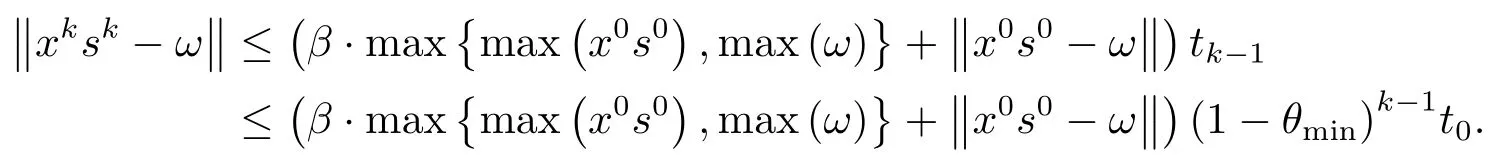
5.數(shù)值算例

為檢驗(yàn)算法2.1的有效性,在Intel(R)Core i5 CPU2.3GHz 8.0內(nèi)存,IOS操作系統(tǒng)的計(jì)算機(jī)上運(yùn)用MATLABR 2016b編程進(jìn)行數(shù)值實(shí)驗(yàn).

在算法2.1中令參數(shù)t0= 1,ε= 10?5.隨機(jī)生成5個(gè)不同規(guī)模的LWCP,且每種規(guī)模產(chǎn)生10個(gè)問(wèn)題,分別取β= 0.7,β= 0.8和β= 0.9進(jìn)行求解.隨機(jī)生成行滿秩矩陣A ∈Rm×n.選取任意起始點(diǎn)(x0,y0,s0)∈F0,權(quán)向量ω >0,按照(4.1)式選擇參數(shù)θ,K.算法的終止準(zhǔn)則為∥xs ?ω∥≤ε,記Gap=∥xs ?ω∥.如表5.1,5.2所示,在算法2.1求解相同規(guī)模的LWCP時(shí)K值上界與迭代次數(shù)和運(yùn)行時(shí)間呈正相關(guān)關(guān)系.在K值上界確定的情況下,m和n對(duì)運(yùn)行時(shí)間和迭代次數(shù)也有較大影響;從數(shù)值試驗(yàn)結(jié)果可知,在t從1減少到0的過(guò)程中,θ單調(diào)遞增,且β的取值越趨向1,算法2.1求解同一LWCP所需的迭代次數(shù)就越少.表中數(shù)據(jù)均為求解不同規(guī)模的LWCP10次結(jié)果的平均值.

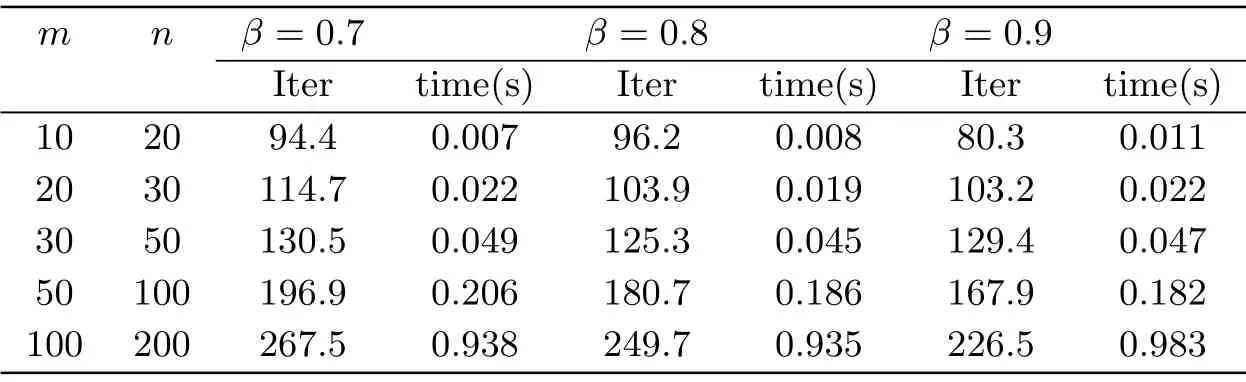
表5.1 K ≤2時(shí)求解不同規(guī)模和β值的LWCP的數(shù)值結(jié)果

表5.2 K ≤0.5時(shí)求解不同規(guī)模和β值的LWCP的數(shù)值結(jié)果

例5.1考慮R6上的LWCP(2.1),其中

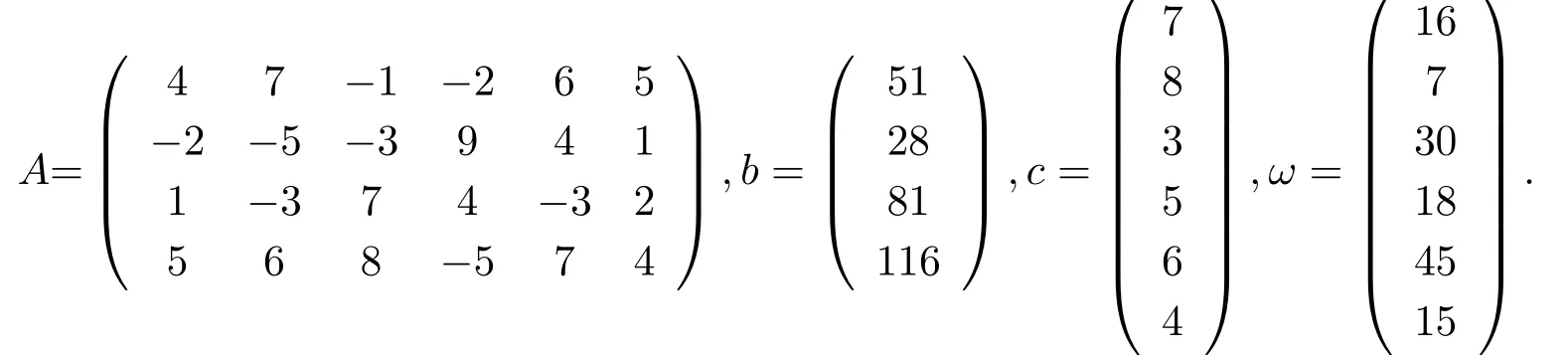
取初始點(diǎn)x0= (2,1,11,5,7,3)T,y0= (0,0,0,0)T,s0= (7,8,3,5,6,4)T,t0= 1,β=0.9.用算法2.1求解例5.1,得到最優(yōu)解x?= (2.100,0.738,10.986,4.836,7.105,3.092)T,y?=?(0.141,0.109,0.035,0.026)T,s?=(7.618,9.486,2.731,3.722,6.334,4.851)T.圖5.1 可知,隨著t的減小,Gap逐漸減小并趨于0,且每步迭代鄰近測(cè)度都小于βt.

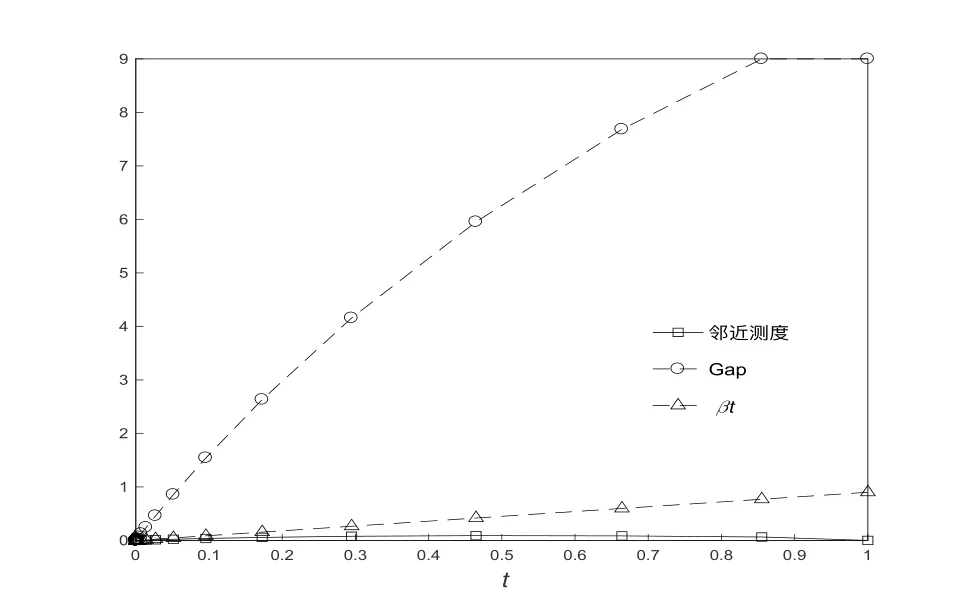
圖5.1 迭代過(guò)程中鄰近測(cè)度及Gap的值