北京大學(xué)附屬中學(xué)(100190) 單治超

均值不等式是高中數(shù)學(xué)的重要內(nèi)容, 其內(nèi)容容易理解,但是具體運(yùn)用時(shí)則靈活多變.國家課標(biāo)對均值不等式的要求難度并不高.但是2020年的北大和復(fù)旦強(qiáng)基計(jì)劃數(shù)學(xué)試題都考查了利用待定系數(shù)法結(jié)合均值不等式解決給定條件下多元函數(shù)的最值問題.我們又注意到前兩年的清華領(lǐng)軍計(jì)劃也都考查了類似的題目.這類題目的頻繁出現(xiàn),使得準(zhǔn)備強(qiáng)基計(jì)劃的同學(xué)必須引起高度重視.為此,我們撰寫本文對這種方法進(jìn)行一點(diǎn)梳理.

我們用到的工具很簡單:

定理1(具有待定系數(shù)的二元均值不等式) 對任意C ＞0,x ＞0,y ＞0,當(dāng)且僅當(dāng)y=C2x時(shí)取等號.

證明顯然.

例1(2020年北大強(qiáng)基計(jì)劃第9 題) 求使得5x+12>xy≤a(x+y) 對所有正實(shí)數(shù)x,y都成立的實(shí)數(shù)的最小值a.

解易見這個(gè)最小值就是二元函數(shù)f(x,y) =在條件x ＞0,y ＞0 下的最大值.對任意C ＞0,

為了讓不等式的右端除以x+y是個(gè)定值, 我們令5 + 6C=即C=此時(shí)我們得到f(x,y) ≤9.很容易驗(yàn)證等號可以取到.所以f(x,y) =在條件x ＞0,y ＞0 下的最大值是9.因此a的最小值是9.

從這個(gè)例題我們領(lǐng)會(huì)到, 利用待定系數(shù)的均值不等式,關(guān)鍵點(diǎn)在于令待定的系數(shù)能夠使得兩個(gè)式子的比例為定值.

我們再做一道例題鞏固對這種方法的理解.

例2(2020年復(fù)旦強(qiáng)基計(jì)劃第2 題)已知實(shí)數(shù)x,y滿足x2+2xy ?1=0,求x2+y2的最小值.

解對任意C ＞0,

為了令不等式的右端與x2+y2的比例為定值, 我們令1+C=即C=于是x2+y2≥容易驗(yàn)證等號可以取到,所以x2+y2的最小值是

前面兩個(gè)例子都是2020年強(qiáng)基計(jì)劃的試題.事實(shí)上,這種方法在以往的清華領(lǐng)軍計(jì)劃試題中已經(jīng)有所考查.

例3(2018年清華領(lǐng)軍計(jì)劃第10 題)設(shè)a,b,c為正數(shù),且a2+b2+c2=1,求a(a+b+c)的最大值.

分析這道例題相對前兩道例題的難度在于出現(xiàn)了三個(gè)變量,但是容易發(fā)現(xiàn)b,c兩個(gè)變量的地位是相同的,因此我們在利用均值不等式對只涉及b,c的解析式進(jìn)行放縮時(shí),不需要利用待定系數(shù)的均值不等式.

解對任意k ＞0,

為了令不等式的右端與a2+b2+c2的比例為定值,我們令于是

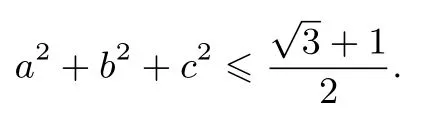
容易驗(yàn)證等號可以取,所以a(a+b+c)的最大值是

2019年清華領(lǐng)軍計(jì)劃還出過一道更難的題,需要利用待定系數(shù)的三元均值不等式.

定理2(具有待定系數(shù)的三元均值不等式) 對任意k ＞0,l ＞0,x ＞0,y ＞0,z ＞0,當(dāng)且僅當(dāng)kx=ly=z時(shí)取等號.

證明顯然.

例4(2019年清華領(lǐng)軍計(jì)劃第23 題)已知ab(a+8b)=20,求a+3b的最小值.

解對任意正實(shí)數(shù)k,l,

為了令不等式的右邊與a+3b的比例是定值,我們需要令

注意到滿足這個(gè)等式的正有序?qū)崝?shù)對(k,l)具有無數(shù)個(gè),但是僅滿足這個(gè)等式的(k,l)不足以讓我們達(dá)到目的,因?yàn)榇藭r(shí)我們必須考慮不等式取等號的條件ka=lb=a+8b能否實(shí)現(xiàn).容易發(fā)現(xiàn),這個(gè)條件能夠?qū)崿F(xiàn)當(dāng)且僅當(dāng)

聯(lián)立方程組(1)(2),它的正實(shí)數(shù)對解只有一個(gè):k=5,l=10.于是可求得a+3b的最小值是5.

我們運(yùn)用例4 的方法,可以對例4 的結(jié)論一般化:

定理3設(shè)p,q是給定的正常數(shù),在已知ab(a+pb)=1,a,b ＞0 的條件下,a+qb的最小值是其中

證明對任意正實(shí)數(shù)k,l,

為了令不等式的右邊與a+qb的比例是定值,我們需要令

不等式取等號的條件是ka=lb=a+pb.這個(gè)條件能夠?qū)崿F(xiàn)當(dāng)且僅當(dāng)

聯(lián)立方程組(1) (2), 它的正實(shí)數(shù)對解只有一個(gè):k0=因此我們就得到了想要的結(jié)論.