Exact soliton solutions in anisotropic ferromagnetic wires with Dzyaloshinskii–Moriya interaction*
Qiu-Yan Li(李秋艷), Dun-Zhao(趙敦), and Zai-Dong Li(李再東),3,4,?
1Department of Applied Physics,Hebei University of Technology,Tianjin 300401,China
2School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,China
3State Key Laboratory of Quantum Optics and Quantum Optics Devices,Shanxi University,Taiyuan 030006,China
4School of Science,Tianjin University of Technology,Tianjin 300384,China
Keywords: bright soliton,black soliton,Dzyaloshinskii–Moriya interaction
1. Introduction
In ferromagnetic wires, there are many nonlinear magnetic excitations, such as spin waves, domain wall, and dynamic solitons.The magnetic domain wall describes the localized states, in which the magnetization gradually inverses its direction and it can be used to store and exchange two bits in race track memory.[1–4]In the last thirty years,physical scientists have mainly used magnetic fields and spin-polarized currents to drive domain wall motion,[5–8]in which the main theoretical method is the Walker method.[9–14]On the other hand,two inverted domain walls can form a dynamic soliton. By continuous deformation it can be reduced to a uniform magnetization. This magnetic soliton can define the typical scale for magnetic texture and enable high density magnetic storage in nanomagnetism.[15–17]
In the inversion symmetry broken system, the research of Dzyaloshinskii–Moriya interaction (DMI)[18,19]has attracted great attention for the effect of spin–orbit scattering of electrons, such as the specific metallic alloys with B20 structure[20–24]and the surface or interface of magnetic multi-layers,[25–29]while it vanishes when the system is centrosymmetric.[30]For this reason, the presence of DMI favors a certain chirality of the magnetization such as skyrmions,[31,32]vortex structures,[33–35]and spin spirals.[36–44]
It has been reported that the DMI can give rise to very interesting phenomena for domain wall dynamics driven by the magnetic fields[45–51]or charge currents.[52–60]Also, various novel property has been clarified in the magnon Hall effect,[61]molecular magnetism,[62]and multiferroicity.[63]Besides the above studies for nonlinear excited states, however the exact soliton solutions have not well explored in ferromagnetic wires with the presence of DMI. In this paper, we obtain three exact soliton solutions in anisotropic ferromagnetic wires with DMI. We find that the DMI affects the velocity, processional frequency,and the internal structure distortion of the solitons.
2. Exact Dzyaloshinskii–Moriya soliton solutions
As a model,we consider a uniaxial anisotropic ferromagnetic wire with DMI. In the continuous limit, the dimensionless Hamiltonian can be written as[57,58]

Equation (2) has a norm form of Landau–Lifshitz type for the magnetization dynamics in a uniaxial anisotropic ferromagnetic wire with DMI.The exact solution of Eq.(2)may be very complex, and the ansatz method is an effective straightforward technique. Firstly, it applies a direct transformation to the nonlinear equation. With some reasonable assumptions,the exact solutions can be constructed effectively by the symbolic computation. In the following, we obtain three exact soliton solutions for Eq.(2).
2.1. Bright Dzyaloshinskii–Moriya soliton
The first type of bright Dzyaloshinskii–Moriya soliton takes the form

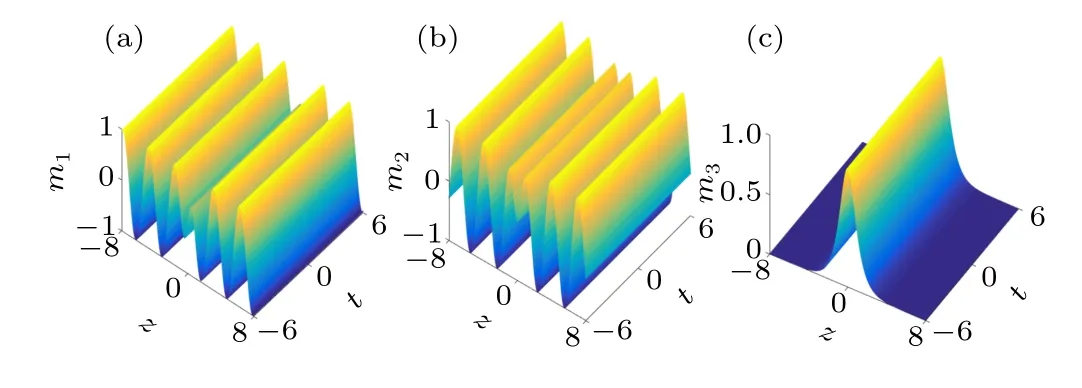
Fig. 1. Evolution of bright Dzyaloshinskii–Moriya soliton solution in Eq. (3). As z →±∞, it reprents a periodic solution, i.e., m3 →0 and m+≡m1+im2=eiφ1. Parameters are k1=2,λz=0.3,and D0=0.5.
By a tedious calculation, we obtain the second type of bright Dzyaloshinskii–Moriya soliton
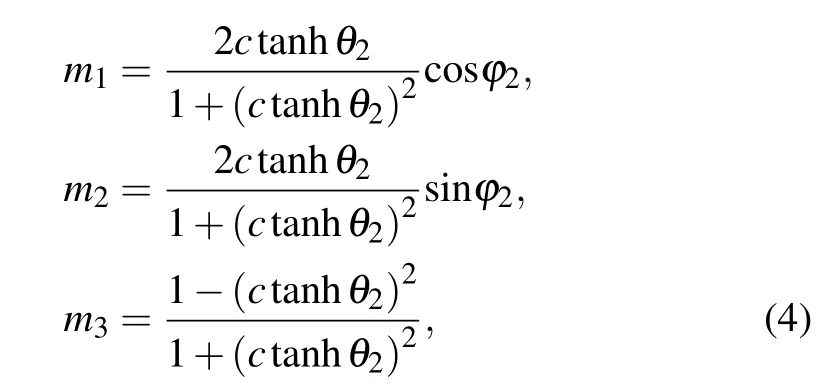
where

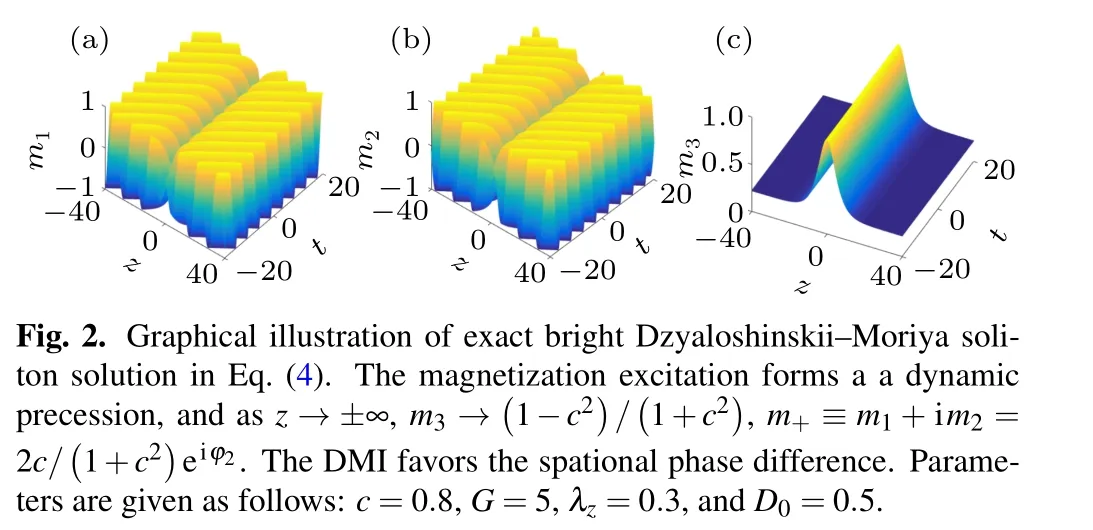
2.2. Black Dzyaloshinskii–Moriya soliton
The black type of Dzyaloshinskii–Moriya soliton takes the form

where

Here a and z3are the only free parameters in the solution. The solution in Eq.(6)represents a black soliton solution of magnetization on a ground state background as shown in Fig. 3.From Fig. 3, we find that equation (6) reduces to the ground state as z →±∞, i.e., m3→1 and m+≡m1+im2→0. In the region of soliton, the components m1and m2precesses around with m3. The precession wave number is D0, and the frequency is ζ. These results show that the DMI favors the spatial phase for the magnetization state, and determines the precession velocity.

Fig.3. Evolution of exact black Dzyaloshinskii–Moriya soliton solution in Eq.(6). The solution of magnetization reduces to the ground state,m3 →1 and m+≡m1+im2 →0 as z →±∞. The DMI fovors the spatial phase for the magnetizaion state. Parameters are given as follows: a=1.5,λz=0.3,and D0=0.5.
3. Conclusion
In this paper, we have constructed the exact soliton solutions of anisotropic ferromagnetic wires with the Dzyaloshinskii–Moriya interaction. The effect of DMI on magnetization motion was studied in detail by using these analytical solutions. These results show that the DMI can affect the existence region of soliton, spin-wave transport, and soliton dynamic properties in the magnetic structures.
- Chinese Physics B的其它文章
- Numerical simulation on ionic wind in circular channels*
- Interaction properties of solitons for a couple of nonlinear evolution equations
- Enhancement of multiatom non-classical correlations and quantum state transfer in atom–cavity–fiber system*
- Protein–protein docking with interface residue restraints*
- Effect of interaction between loop bases and ions on stability of G-quadruplex DNA*
- Retrieval of multiple scattering contrast from x-ray analyzer-based imaging*

