Syed Tahir Raza Rizvi, Ishrat Bibi, Muhammad Younis, and Ahmet Bekir

1Department of Mathematics,COMSATS University Islamabad,Lahore Campus,Pakistan

2Punjab University College of Information Technology,University of the Punjab,Lahore,Pakistan

3Neighbourhood of Akcaglan,Imarli Street Number 28/4,26030,Eskisehir,Turkey

Keywords: Hirota bilinear method,soliton interaction,evolution equations

1. Introduction

A nonlinear pulse or wave packet that can spread continuously over incredibly long distances without decreasing or changing shape is called soliton. The presence of these pulses in optical fibers is generally based on a careful balance between the consequences of group velocity dispersion and self-phase modulation. Erection of soliton solutions to the nonlinear evolution equations (NLEEs) arising in nonlinear science plays an important role to understand nonlinear phenomena. Solitons have lot of applications in physics,optical science, applied mathematics and engineering problems. Nonlinear equations are closely connected to soliton forms of well-known integrable equations, namely Burgers, Korteweg–de Vries, modified Korteweg–de Vries, sine-Gordon and Schr¨odinger equations.[1–12]In an optical communication system, to enhance the fiber’s information carrying capacity,it is essential to arrange the solitons close to each other. Soliton interactions formed by pairs of optical pulses.There are several new nonlinear models that can be fully integrated. Such systems can be described as flows in multisoliton fields that explain the self-interaction of single solitons. Tanh method,[13]The Hirota bilinear method (HBM),[14,15]Trail method,[16]multiple exp-function method,[17]transformed rational function method,[18,19]Cole–Hopf transformation[20]and many others have been used to find soliton solutions for various forms of NLEEs. Yu et al. obtained one- and twosoliton solutions using the Hirota bilinear method.[21]They studied amplification, oscillation and phase shift for solitons.Liu et al. discussed control and generation of multiple solitons under the influence of parameters.[22]Wazwaz studied the multiple soliton solution of sech-squared type for the shallow water wave equation using the Hirota bilinear method.[23]Wazwaz used a simplified form of the Hirota method to obtain one- and two-soliton solutions to the nonlinear sinh-Gordon equation in(1+1),(2+1)and(3+1)dimensions.[24]In this paper,we study two renowned NLEEs,i.e.,the Cahn–Allen(CA)equation and the Brethorton equation for one-and two-soliton solutions with the help of the HBM.

The paper is organized as follows: In Section 2,we study the CA equation for one- and two-soliton solutions with the help of the HBM.In Section 3,we obtain one-and two-soliton solutions to the Brethorton equation by the aid of the HBM.In Section 4, we compare and discuss our results. In Section 5,we give conclusions of our results.

2. The Cahn–Allen equation

The CA equation is studied in anti-phase boundary motion and it is used in phase-field models to discuss the free boundary problems. The CA equation is a mathematical physics reaction-diffusion equation that explains the method of separation of phases in multi-component alloy structures,including order–disorder transformations. The mathematical model for the CA equation is given by[25]

2.1. One-soliton transformation

To obtain the one-solitary wave solution,we consider

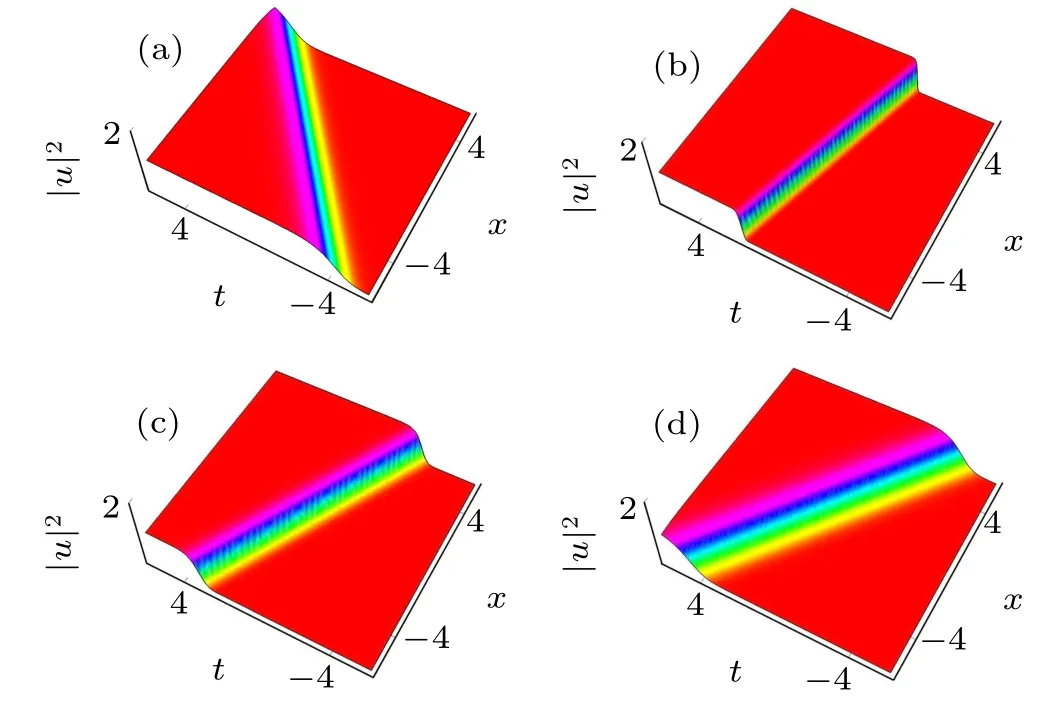
Fig. 1. One-soliton solution to the CA equation: (a) p1 =-1.3, (b)p1=3.8,(c) p1=2,(d) p1=1.4.

Figure 1 shows the one-soliton transformation for the CA equation for different values of parameter p1.

2.2. Two-soliton interaction

To obtain two-soliton solution,we consider

Figure 2 shows the m-shaped anti-dark soliton as two-soliton interaction for different values of parameters p1and p2in the CA equation.

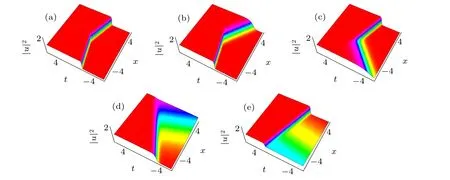
Fig.2. Two-soliton solution to the CA equation: (a) p1 =-3.9, p2 =3.3; (b) p1 =-3.9, p2 =1.5; (c) p1 =-1, p2 =3.3; (d) p1 =-1.9,p2=0.33;(e) p1=3.4, p2=-0.19.

In the following section,we will find one-and two-soliton solutions for the Brethorton equation.

3. The Bretherton equation

One of the recently studied nonlinear ecological equations (NLEEs) is the Bretherton equation. This equation appears in different fields of applied and nonlinear sciences such as physics,biosciences as well as engineering. The governing model for the Brethorton equation is given by[16]

3.1. One-soliton transformation

To obtain one-soliton solution,we take

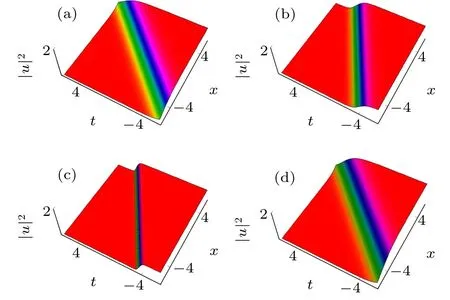
Fig.3. One-soliton solution for the Brethorton equation with the positive case:(a)a=-1,b=-1,p1=1,c=1;(b)a=-3,b=-1,p1=1,c=1;(c)a=-1,b=-0.9,p1=3,c=1;(d)a=-1,b=-1,p1=1,c=0.8.

First we consider the positive case. Figure 3 shows the kinktype soliton solution as the one-soliton transformation for different values of parameters p1,a,b and c. We have

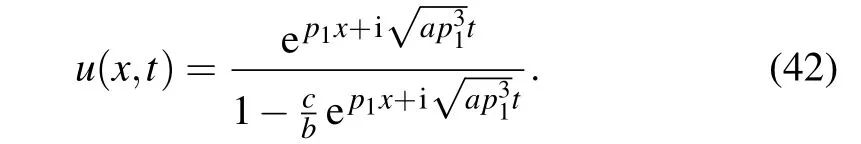
Here we consider the negative case. Figure 4 shows the one-soliton solution for different values of parameters p1, a,b,and c. We have

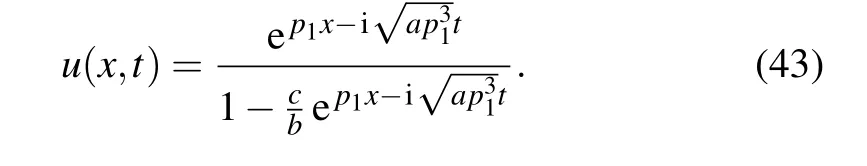
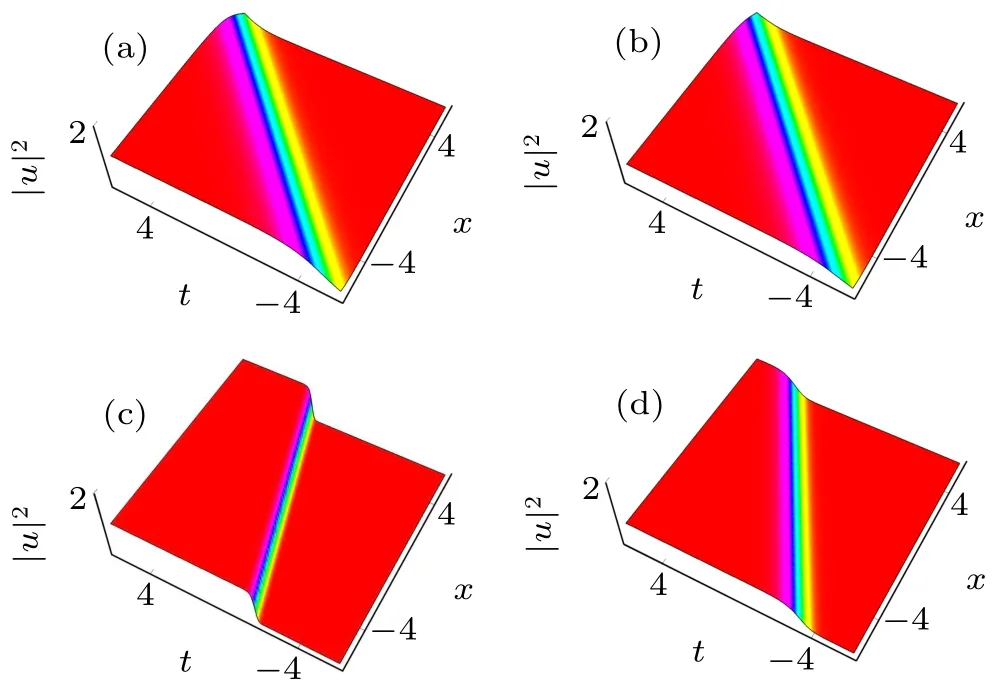
Fig. 4. One-soliton solution for the Brethorton equation with the negative case: (a) a=1, b=-1, p1 =-1.1, c=1; (b) a=1, b=-1,p1 =-1.1, c=1.3; (c) a=4, b=-1, p1 =-3, c=1; (d) a=2,b=-1.6, p1=-1.5,c=2.

3.2. Two-soliton interaction

To find two-soliton interaction,we consider

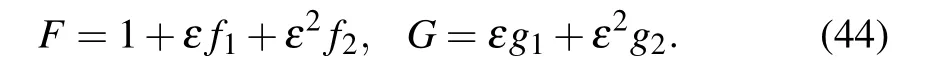
Substituting Eq.(40)into Eq.(26),and equating the coefficient of ε2

Now consider

Substituting Eq.(42)into Eq.(41)yields

Substituting Eq.(40)into Eq.(30)and equating the coefficient of ε2,we have

which implies

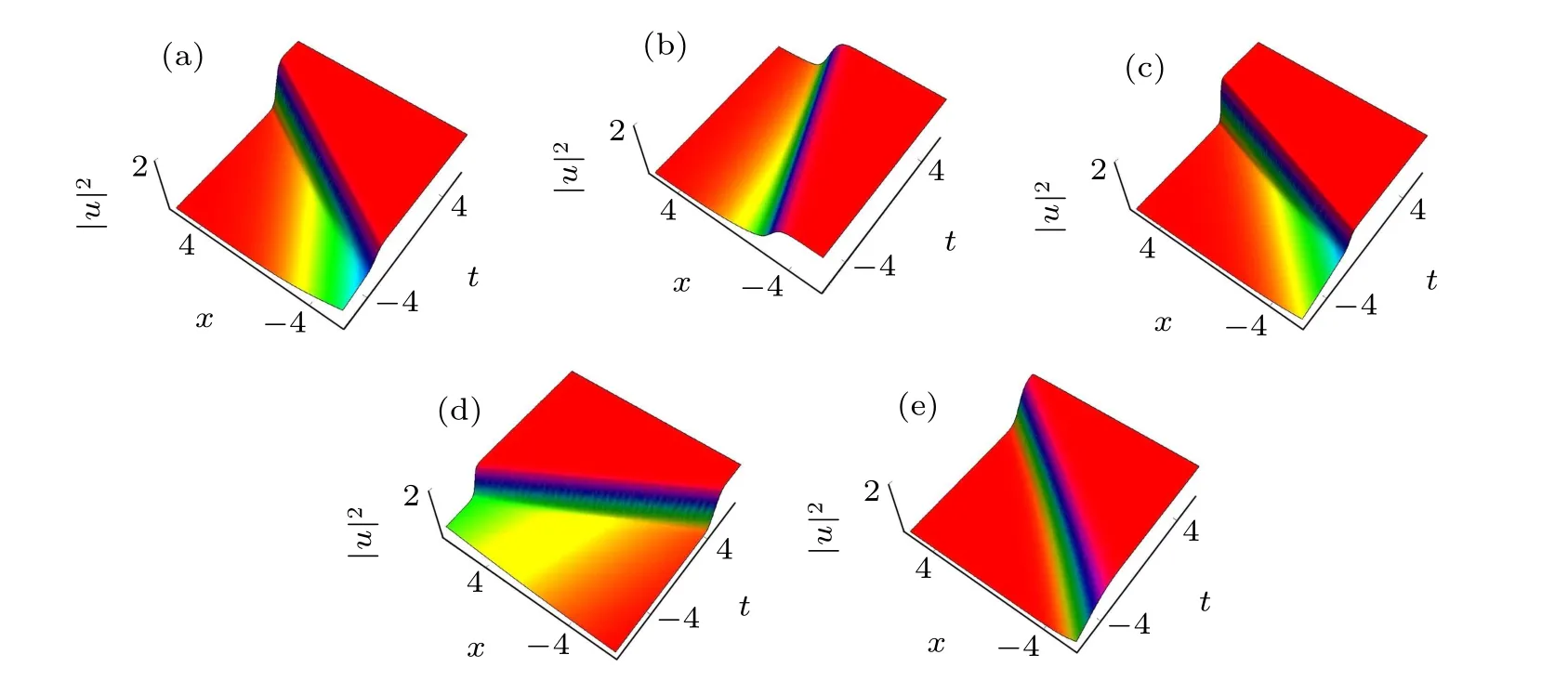
Fig.5. Two-soliton interaction for the Brethorton equation with positive case: (a)a=1,b=-1,c=0.8, p1=-0.38, p2=-3;(b)a=0.05,b=-1,c=0.8, p1=-0.38, p2=-3;(c)a=3,b=-1,c=0.8, p1=-0.38, p2=-3;(e)a=-1,b=-1,c=0.8, p1=0.1, p2=3;(f)a=1,b=-1,c=0.9, p1=-1, p2=-2.

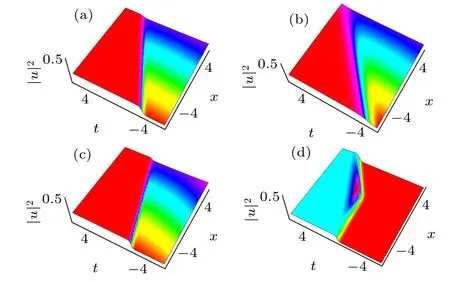
Fig.6. Two-soliton interaction for the Brethorton equation with negative case: (a)a=1,b=-1,c=2.3, p1=-0.36, p2=0.19;(b)a=1,b=-1, c=2.3, p1 =-1.5, p2 =0.19; (c) a=3, b=-1, c=2.3,p1=-3.6, p2=0.19;(d)a=1,b=-1,c=3, p1=-2.8, p2=-2.2.

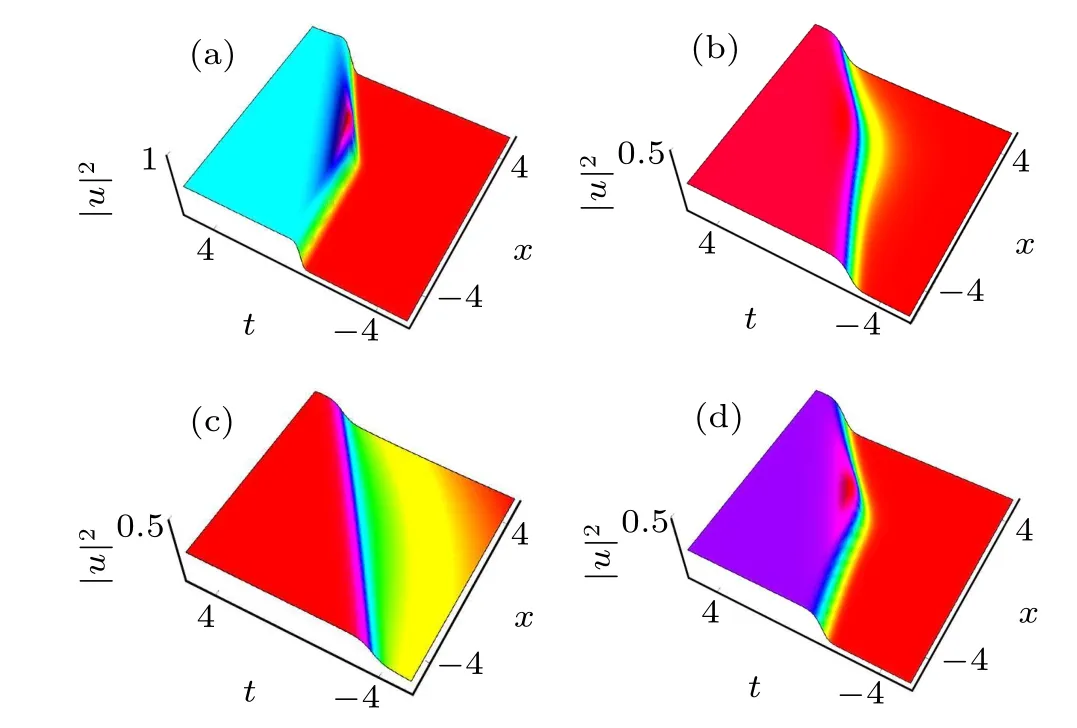
Fig. 7. Two-soliton interaction for the Brethorton equation with negative case: a=1, b=-1, c=1.45, p1 =-2.8, p2 =-2.2, a=1,b=-1, c=2.1, p1 =-1.9, p2 =-0.44, a=1, b=-1, c=2.1,p1=-1.9, p2=-0.1,a=1,b=-1,c=2.1, p1=-1.9, p2=-1.

4. Results and discussion

In this section, we compare our results with the existing results of the CA and Brethorton equations. The CA equation is studied in anti-phase boundary motion and it is used in phase-field models to discuss the free boundary problems. Yokus and Bulut discussed the CA equation using the finite difference method and operators.[25]Bulut et al. also obtained new exponential prototype structures for the CA equation with the help of the Bernoulli sub-equation function method.[16]Tascan and Bekir established the traveling wave solutions to the CA equation with the aid of the first integral method.[27]Ma and Fuchssteiner studied the Kolmogorov–Petrovskii–Piskunov (KPP) equation (the CA equation is the special case of the KPP equation)for soliton solutions with the aid of the Cole–Hopf transformation.[20]We obtain one- and two-soliton solutions to the CA equation with the help of the HBM.Another very famous model is the Brethorton equation(Brethorton equation),used in dispersive wave systems. Triki et al. studied the Brethorton equation to find the topological and non-topological soliton solution using the ansatz and trail solution method.[28]Oguz et al. obtained the traveling wave solutions for the Brethorton equation with the aid of the homogenous balance method.[29]In this paper, we obtain oneand two-solitons for the Brethorton equation using the HBM.

A family of solitary waves and soliton solutions are obtained in this paper. Different types of solitary waves are shown when different values are assigned to unknown parameters for one-and two-soliton solutions. We also illustrate the three-dimensional aspects of these models. The configuration of the figures is represented in order of observing the physical appearance of the model by assigning appropriate values to the parameters.The same wave solutions shown in different shapes can be seen in Fig.1. Figure 1 depicts the one-soliton solution to the CA equation for different values of p1.Figure 2 shows the m-shaped anti-dark soliton as two-soliton interaction for different values of parameters p1and p2for the CA equation. In Fig. 3, we consider the positive case and show the kink-type soliton solution for the Brethorton equation as the one soliton transformation for different values of parameters p1, a, b, and c. In Fig. 4, we consider the negative case and show the one-soliton solution for the Brethorton equation using different values of parameters p1, a, b and c. Figure 5 shows the two-soliton solution for the Brethorton equation using different values of parameters p1, p2, a, b and c with the positive case. In Figs.6 and 7,we consider the negative cases for the two-soliton solution using different values of parameters p1, p2,a,b and c.

5. Conclusions

In summary, we have studied soliton interaction properties for two nonlinear evolution equations,i.e.the CA equation and the Brethorton equation,using the Hirota bilinear method.Many researchers obtained exact and traveling wave solutions for both the models. However,we obtain one-soliton transformation and two-soliton interaction for the CA equation and the Brethorton equation. We also give the graphical interpretation for our obtained results. The results are new and novel.