王美娜,唐孝敏

(黑龍江大學數(shù)學科學學院,黑龍江 哈爾濱150080)

1 引言

Poisson代數(shù)源于對Poisson幾何的研究,自然出現(xiàn)于哈密頓力學,且是量子群研究的中心.簡單來說,一個Poisson代數(shù)(A,?,[?,?]),就是同時帶有代數(shù)和李代數(shù)兩種結構的代數(shù),且這兩種代數(shù)結構之間要滿足Leibniz法則.

鑒于Poisson幾何與數(shù)學的緊密聯(lián)系,使它受到了許多研究者的關注.其中以Lichnerowicz[1]和Weinstein[2]最為具有代表性.近年來,隨著Poisson代數(shù)的發(fā)展,其結構問題得到了一些新成果,例如,文獻[3]研究了扭Heisengerg-Virasoro代數(shù)上的Poisson結構,文獻[4]研究了Witt代數(shù)和Virasoro代數(shù)上的Poisson結構,文獻[5]研究了Toroidal李代數(shù)上的Poisson結構,文獻[6]研究了擴張仿射李代數(shù)上的Poisson結構,文獻[7]確定了李代數(shù)W(2,2)上的Poisson結構,并改進了文獻[4]中的結果.另外,文獻[8]得到Lie理論中一類Poisson結構的構造,文獻[9]研究了Hall代數(shù)上的Poisson結構,文獻[10]研究了張量代數(shù)上一種帶辮子的Poisson結構.

近20年,Poisson代數(shù)引起了越來越多的研究人員的關注,并在結構理論和表示理論方面取得了很多結果.Schrdinger-Virasoro代數(shù)是一類重要的無限維李代數(shù),在數(shù)學和物理學的許多分支中都有著廣泛的應用.許多研究者研究了(廣義)Schrdinger-Virasoro代數(shù)的結構與表示理論等,見文獻[11]和[12]等,但其Poisson結構的研究尚未實現(xiàn).本文將研究Schrdinger-Virasoro代數(shù)上的Poisson 結構.

2 預備知識

本節(jié)主要介紹相關李代數(shù)及Poisson代數(shù)的基本概念.

定義2.1[11]Schr?dinger-Virasoro代數(shù)SV是一個無限維李代數(shù),具有C-基{Ln,Yn,Mn|n∈Z},且滿足如下李關系式

記SVi為由{Li,Yi,Mi}所張成的三維向量空間.SV關于Cartan子代數(shù)CL0有分解SV=⊕i∈ZSVi.

定義2.2[3]Poisson代數(shù)(A,?,[?,?])是域C上的一個向量空間A,同時具有代數(shù)乘法?和李代數(shù)乘法[?,?],且滿足Leibniz法則:[z,x?y]=[z,x]?y+x?[z,y],?x,y,z∈A.若乘法?滿足結合律,則稱Poisson代數(shù)是結合的;若乘法?滿足交換律,則稱Poisson代數(shù)是交換的.

3 李代數(shù)SV上的Poisson結構

本節(jié)將給出Schr?dinger-Virasoro代數(shù)上的Poisson結構.注意到本文討論的是非結合Poisson結構,推廣了結合的情形.

引理3.1若在李代數(shù)SV上存在一個代數(shù)乘積?,使得(SV,?,[?,?])成為一個Poisson代數(shù),則SVi?SVj?SVi+j,?i,j∈Z.

證對任意的x∈SVi,y∈SVj,有

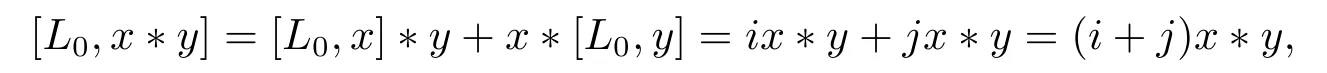
即x?y∈SVi+j.因此,對任意的i,j∈Z,都有SVi?SVj?SVi+j.

定理3.2SV上的任何Poisson結構都具有如下形式

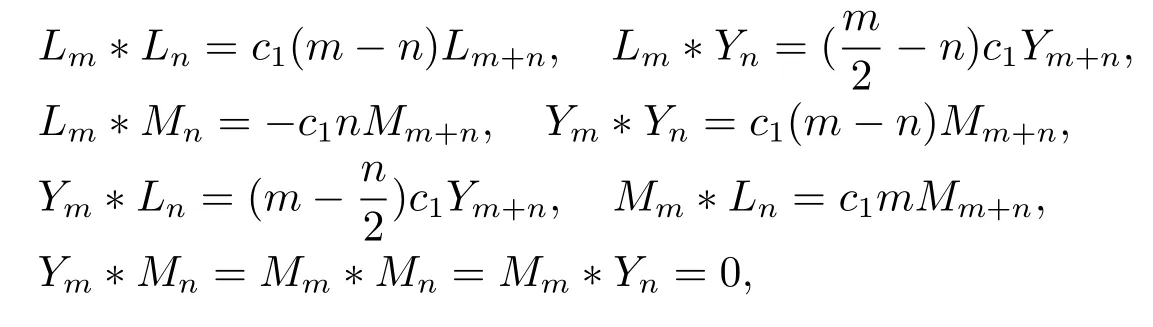
?m,n∈Z,其中c1∈C.

證根據引理3.1易知Mm?Mn∈CMm+n,由此可假設

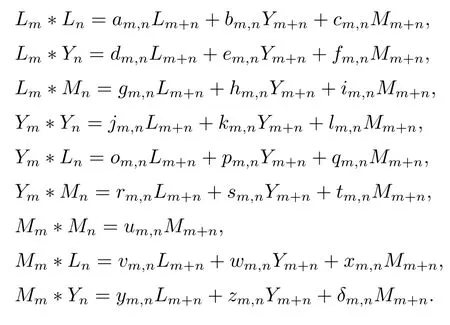
下面分10步來證明定理.