LIPSCHITZ TYPE CHARACTERIZATIONS FOR BERGMAN-ORLICZ SPACES AND THEIR APPLICATIONS?
Rumeng MA (馬茹夢) Jingshi XU (徐景實)?
School of Mathematics and Computing Science, Guilin University of Electronic Technology,Guilin 541004, China
E-mail : rumengmashuxue@163.com; jingshixu@126.com

Given a convex function Φ :[0,+∞)→ [0,+∞), we say that Φ is a growth function if it is a continuous and non-decreasing function.
For a growth function Φ,the Orlicz space LΦ(Bn,dνα)is the space of functions f such that
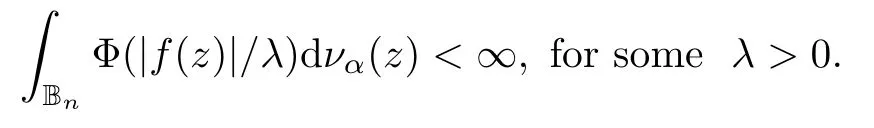
Let H(Bn)denote the space of holomorphic functions on Bn.The weighted Bergman-Orlicz spaceis the subspace of LΦ(Bn,dνα)consisting of holomorphic functions. When Φ(t)=tpfor t ∈ [0,∞) and p ∈ (0,∞), the associated weighted Bergman-Orlicz space is the classical Bergman space
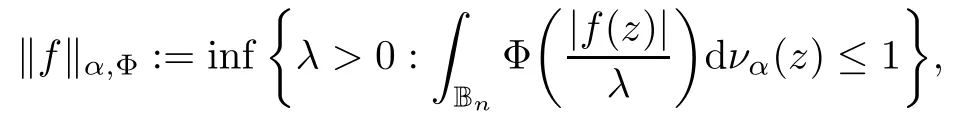
A growth function Φ is said to be of upper type q ≥ 1 if there exists C > 0 such that, for s>0 and t ≥1,
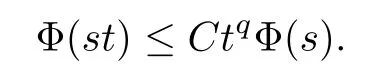
We denote by Uqthe set of growth functions Φ of upper type q (for some q ≥ 1) such that the functionis non-decreasing.
We say that a growth function Φ is of lower type p>0 if there exists C >0 such that, for s>0 and 0 We denote by Lpthe set of growth functions Φ of lower type p (for some p ≤ 1) such that the functionis non-increasing. Given f ∈H(Bn), we denote the radial derivative of f at z by The complex gradient of f at z is defined by and the invariant complex gradient of f at z is given by where ?zis the automorphism of Bnmapping 0 to z. The following lemma is Theorem 1.2 in[12],which characterized the Bergman-Orlicz spaces by derivatives: Lemma 1.1Suppose that α > ?1. Assume that Φ ∈ Uq∪ Lp, and that f is holomorphic in Bn. Then the following conditions are equivalent: For any a ∈ Bn, let ?abe a biholomorphic map on Bnsuch that ?a(0)=a andFor an explicit formula of ?a, see [15]. The Bergman metric on Bnis the following distance: It follows that ρ(z,ω) := |?z(ω)| is also a distance function on Bn. ρ is the so called pseudohyperbolic metric on Bn. The Euclidean metric on Bnis still denoted by |z ? ω|. The main results of the article are the following: Theorem 1.2Assume that Φ ∈ Uq∪ Lp, α > ?1 and f ∈ H(Bn). Then the following conditions are equivalent: (b) There exists a continuous function g in LΦ(Bn,dνα) such that, for all z and ω in Bn, (c) There exists a continuous function g in LΦ(Bn,dνα) such that, for all z and ω in Bn, Theorem 1.3Letting α > ?1, f belongs toif and only if it is the case that (i) If Φ ∈ Uq, then there exists a continuous function g in LΦ(Bn,dνm+α) (m ∈ [q,∞))such that, for all z and ω in Bn, or (ii) If Φ ∈ Lp, then there exists a continuous function g in LΦ(Bn,dνm+α) (m ∈ [1,∞))such that, for all z and ω in Bn, Theorems 1.2 and 1.3 were obtained by Wulan and Zhu in [13]for when Φ(t) = tpfor t ∈ [0,∞) and p ∈ (0,∞). We shall give the proofs of Theorems 1.2 and 1.3 by using the method of [13]in Section 2. In Section 3, we shall give lifting functions from the disk to the bidisk. To prove Theorem 1.2, we need some preliminaries. We first recall some results about the hyperbolic and pseudo-hyperbolic metric. For any r ∈ (0,1) and z ∈ Bn, we let D(z,r) := {ω ∈ Bn: ρ(ω,z) < r} be the pseudohyperbolic disk centered at z with radius r.If r is fixed,then the volume of D(z,r)is comparable to (1 ?|z|2)n+1; see Lemma 1.23 in [15]. For any R > 0 and z ∈ Bn, we let E(z,R) := {ω ∈ Bn: β(ω,z) < R} be the hyperbolic disk centered at z with radius R. If r ∈(0,1) and then it is clear that E(z,R)=D(z,r). Consequently, if R is fixed, then the volume of E(z,R)is comparable to (1 ?|z|2)n+1as well. In the sequel, we shall use C to denote a constant which is different from line to line. Lemma 2.1([15], Lemma 2.20) For each r ∈ (0,∞), there exists a positive constant Crsuch that for all z,ω ∈ Bnwith β(z,ω) Lemma 2.2([15], Lemma 2.24) Suppose that r ∈ (0,1), p ∈ (0,∞), and α > ?1. Then there exists a positive constant C such that for all z ∈Bnand all holomorphic functions f in Bn. Lemma 2.3([13], Lemma 5.2) Suppose that z ∈ Bnand ω = tz, where t is a scalar.Then Lemma 2.4Let Φ ∈ Lp. Then the growth function Φp= Φ(t1/p) is in U1/p. Indeed, for t ≥1 and s>0, we have that where the inequality follows from the fact that Φ(t)/t is non-increasing. Lemma 2.5([15], Theorem 1.12) Let c ∈ R and t ∈ (?1,∞). For z ∈ Bn, define When c<0, Icand Jc,tare bounded in Bn. When c>0, The notation a(z)~b(z) means that the ratiohas a positive finite limit as |z|→1. Now we give the proof of Theorem 1.2. We shall use the idea in [13]and divide the proof into two steps. Proof of Theorem 1.2 Step 1We prove(a)?(b). First we assume that there exists a continuous function g ∈ LΦ(Bn,dνα) such that (1.1) holds. For fixed the z in Bn, let ω =tz,where t is a scalar. Dividing both sides of (1.1) by |z ? ω| for allin Bn, we have that Letting t tend to 1 and using Lemma 2.3, we obtain that for all z ∈ Bn. Since g ∈ LΦ(Bn,dνα), we have (1 ? |·|2)|Rf(·)|∈ LΦ(Bn,dνα). By Lemma 1.1 we have Next, by the Newton-Leibniz formula, for any holomorphic function f in Bnand z ∈Bn,we have that For ρ(z,0) < r, where r ∈ (0,1) is any fixed radius in the pseudo-hyperbolic metric, we have that It is easy to see that in the relatively compact set D(0,r), the Euclidean metric is comparable to the pseudo-hyperbolic metric. It is also easy to see that|?f(u)| is comparable toin the relatively compact set D(0,r). Therefore there is a positive constant C depending only on r such that for all z ∈ D(0,r). Replacing f by f ? ?ωand z by ?ω(z)and then using the Mbius invariance of the pseudo-hyperbolic metric and the invariant gradient, we obtain for all z and ω in Bn, with ρ(z,ω) Let It is easy to see that g is continuous on Bn. If ρ(z,ω) Obviously, we also have If ρ(z,ω)≥ r, then we obtain that From the above estimates we obtain that for all z,ω in Bn. This means that there exists a continuous function g such that (1.1) holds.To complete this step we should show that g ∈ LΦ(Bn,dνα). Since f is already in LΦ(Bn,dνα),it suffices for us to show that h ∈ LΦ(Bn,dνα). Since D(z,r) = E(z,R) if r and R satisfy (2.1), we can choose r′∈ (0,1) such that D(z,r′) = E(z,2R) for all z ∈ Bn. For any u ∈ E(z,R) and any ω1∈ E(u,R), we have that β(ω1,u) Thus,ω1∈ E(z,2R);that is,E(u,R)? E(z,2R).Equivalently,we have that D(u,r)? D(z,r′)whenever u ∈D(z,r). Put By the definition of h(z), we obtain that By Lemma 2.2 we have that It follows from the above fact and Lemma 2.1 that there exists a positive constant C that depends only on r such that, for all z ∈Bn, By Lemma 2.5, there exists a C(z) such thatis a probability measure and C(z) is between positive numbers C1and C2. When Φ ∈ Uqand pΦ=1 we have that Then we have that Using the convexity of Φ and Jensen’s inequality we have that Integrating both sides of the above inequality over Bnwith respect to dνα(z)and using Fubini’s theorem and Lemma 2.5, we have that where we chose β > α. The last inequality follows from Lemma 1.1. Hence, h ∈ LΦ(Bn,dνα). When Φ ∈ Lpand pΦ=p, we have that By Lemma 2.4 we know that Φp(t) = Φ(t1/p) ∈ U1/p. By the above argument, there exists λ>0 such that Integrating both sides of the above inequality over Bnwith respect to dναand using Fubini’s theorem and Lemma 2.5, we have that Thus we have that Step 2(a) ? (c). If the condition (1.2) holds, we divide both sides of (1.2) by |z ? ω|and take the limit as ω → z. Then we have (1 ? |z|2)|Rf(z)|≤ 2g(z) for all z ∈ Bn. It follows from Lemma 1.1 that We now turn to proving Theorem 1.3. Proof of Theorem 1.3Ifby Step 1 of the proof of Theoren 1.2, there exists a continuous function g1∈ LΦ(Bn,dνα) such that Due to the fact that ρ(z,ω):=|?z(ω)|, by Lemma 1.2 in [15]we have that By the Cauchy-Schwarz inequality, we have thatThen we obtain thatfor all z,ω in Bn. Therefore, By the triangle inequality, we have that We obtain Since g1∈ LΦ(Bn,dνα), we have (1 ? |·|2)g(·)∈ LΦ(Bn,dνα). (i) When Φ ∈ Uqand m ∈ [q,∞), we have that Thus g ∈ LΦ(Bn,dνm+α) for m ∈ [q,∞). (ii) When Φ ∈ Lp, by Lemma 2.4 we know thatThen we have that Due to m ≥ 1, we have that (1 ? |z|2)m?1≤ 1. Therefore we have that g ∈ LΦ(Bn,dνm+α) for m ∈ [1,∞). On the other hand, if there exists a continuous function such that and if we divide both sides of above inequality by |z ? ω| and take the limit as ω → z, then we obtain that Since g ∈ LΦ(Bn,dvα), we have(1 ?|·|2)|Rf(·)|∈ LΦ(Bn,dvα), and by Lemma 1.1 we get thatThus the proof is complete. Let D2n= Bn× Bndenote the bidisk in C2nand let H(D2n) denote the space of all holomorphic functions in D2n. For Φ ∈ Uq∪ Lpand α > ?1, we defineas the space of functions f ∈H(D2n) such that These are also called weighted Bergman-Orlicz spaces. We consider the symmetric lifting operator L:H(Bn)→H(D2n) defined by In [13]Wulan and Zhu considered the boundedness of the lifting operator L between the Bergman spaces for n=1. If α > ?1 and p ∈ (0,α+2), then the lifting operator L is bounded fromIf α > ?1, p> α +2, and β is determined by 2(β +1)=p+ α, then L is bounded fromNow we generalize these results to the Bergman-Orlicz spaces. Theorem 3.1Suppose that α > ?1. If Φ ∈ Uq∪ Lpand q ∈ [1,n+1+ α), then the symmetric lifting operator L is bounded from ProofGivenby Theorem 1.2 we have a continuous function g ∈ LΦ(Bn,dνα)such that Since q ∈ [1,n+α+1), by Lemma 2.5 there exists a positive constant C such that Then, by the closed graph theorem, the operator L:is bounded. (ii) When Φ ∈ Lp, pΦ= p, by Lemma 2.4 we know that Φp(t) = Φ(t1/p) ∈ U1/p. By (3.1)we have that Then we have that Using the convexity of Φpwe have that By Lemma 2.5 there exists a positive constant C >0 such that We have the following result if Theorem 3.2Suppose that α > ?1. Assume that any of the two following conditions is satisfied: (i) Φ ∈ Uqwith q ∈ (n+1+ α,∞) and β is defined by 2β +n+1=q+ α; (ii) Φ ∈ Lpand β is defined by 2β +n+1=pq+ α for some Then the symmetric lifting operator L is bounded from Proof(i) If Φ ∈ Uqwith q ∈ (n+1+ α,∞) and β determined by 2β +n+1 = q+ α,then givenby Theorem 1.2 we have a continuous function g ∈ LΦ(Bn,dνα) such that (3.1) holds. In a fashion similar to the proof of Theorem 3.1, we have that Since q ∈ (n+1+ α) and 2β +n+1 = q+ α, we have that β > α, and by Lemma 2.5 there exists a positive constant C such that We then obtain that (ii) When Φ ∈ Lp, and β is determined by 2β +n+1 = pq+ α for someby Lemma 2.4 we know that Φp(t) = Φ(t1/p) ∈ U1/p. Therefore, using the convexity of Φpand Jensen’s inequality, we have that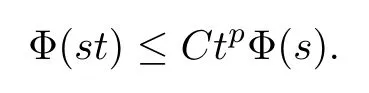

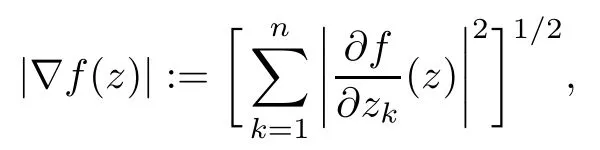




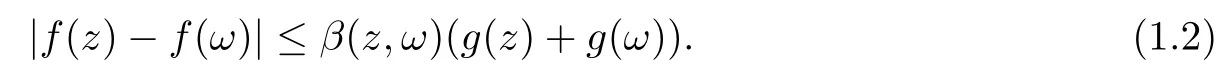


2 Proofs of Theorems 1.2 and 1.3




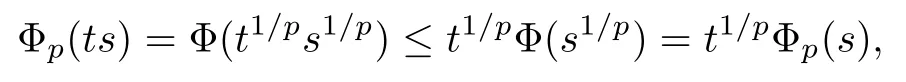
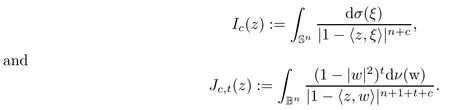
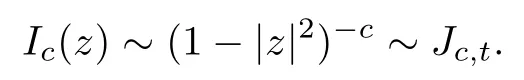
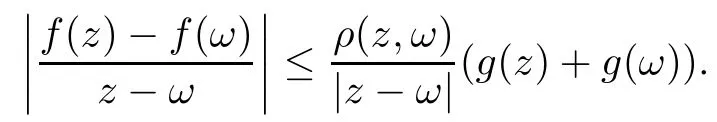
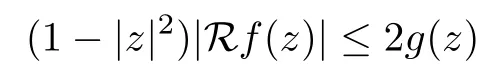
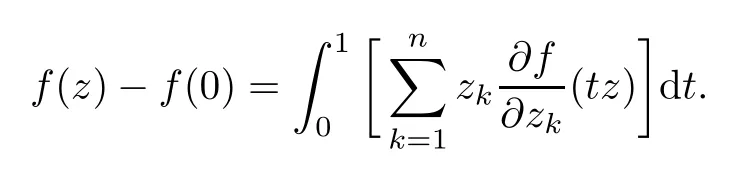

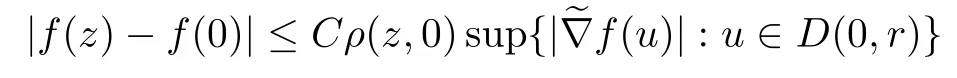
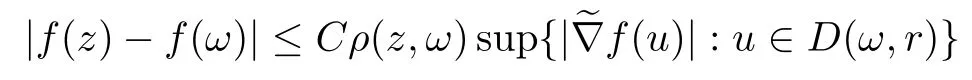
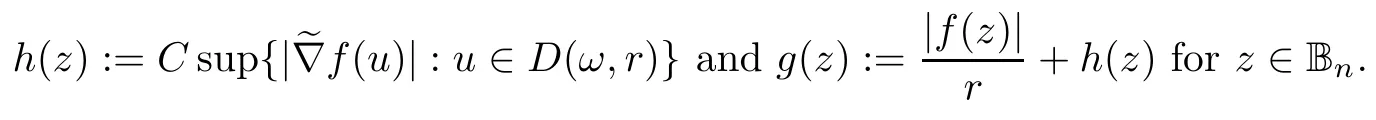



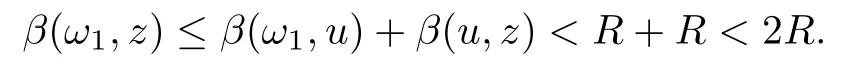
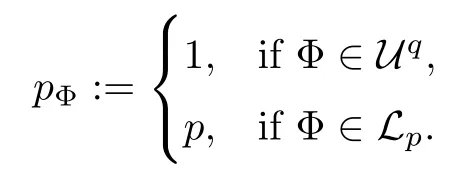
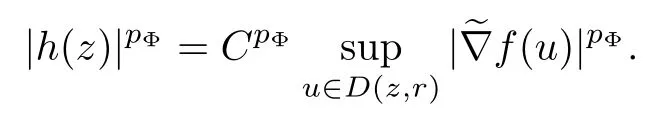




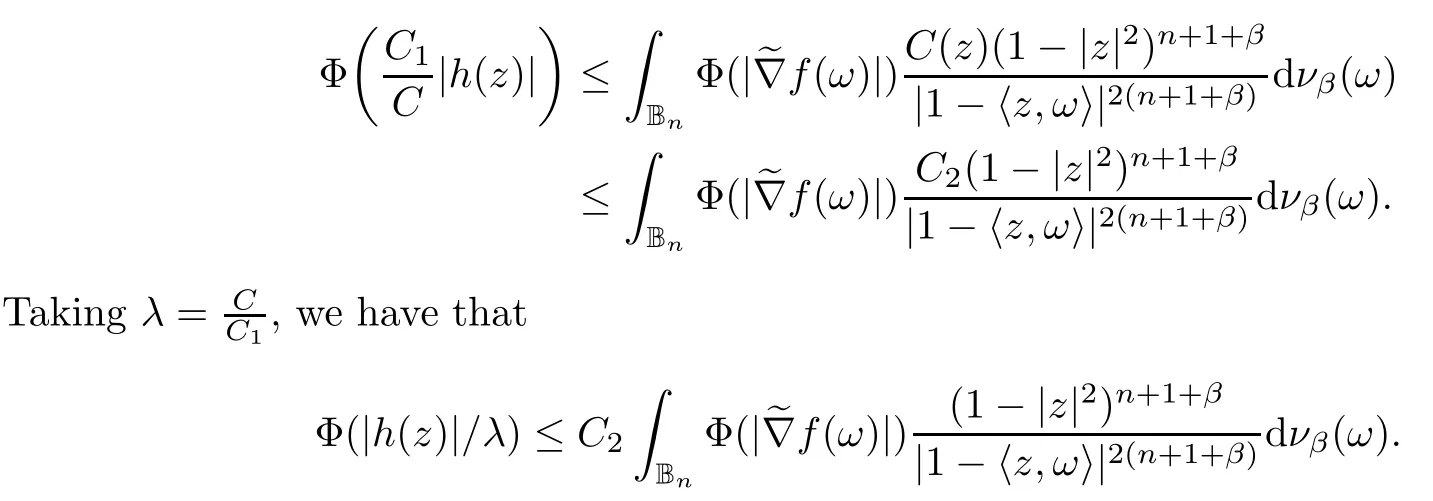

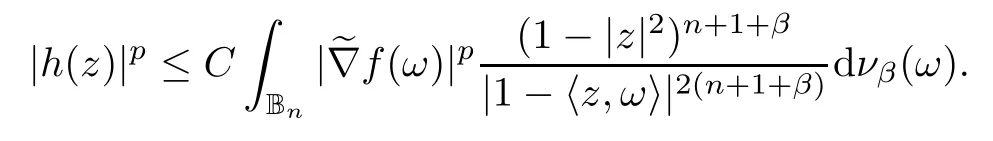

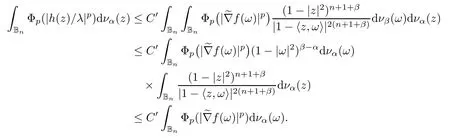

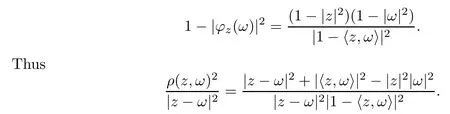
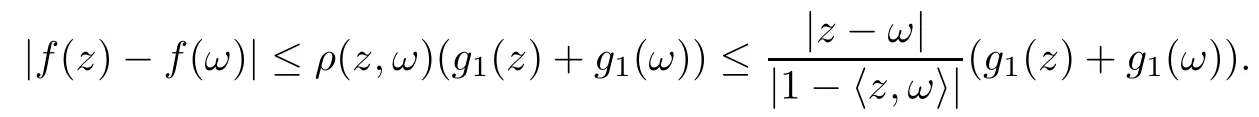

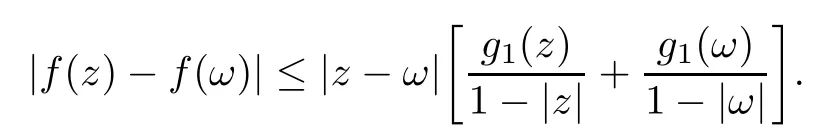


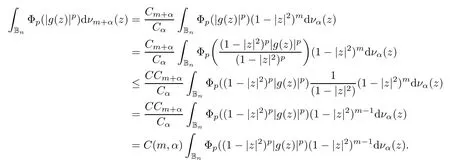



3 Lifting Functions from the Disk to the Bidisk
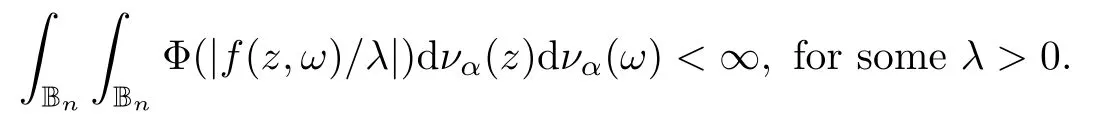
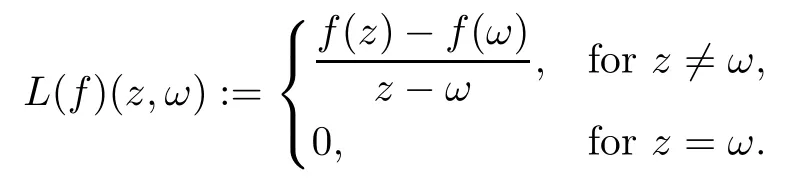
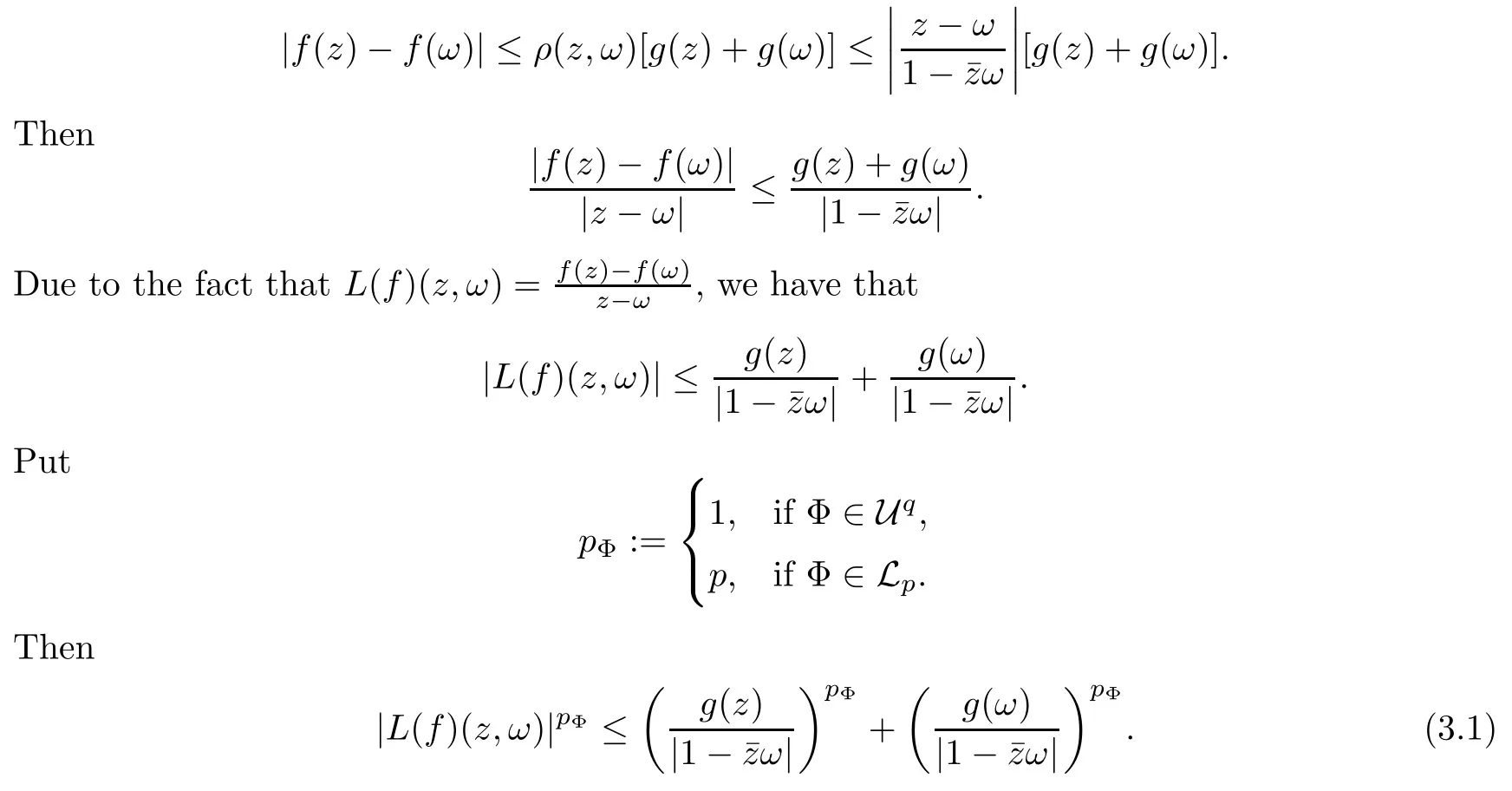


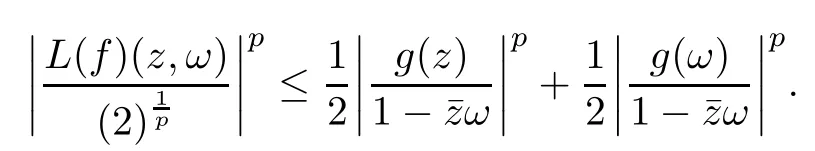
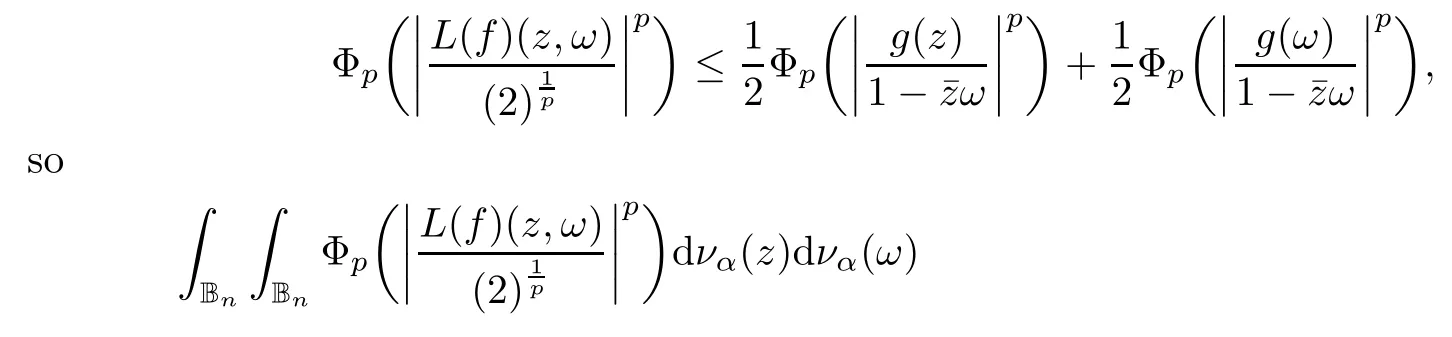
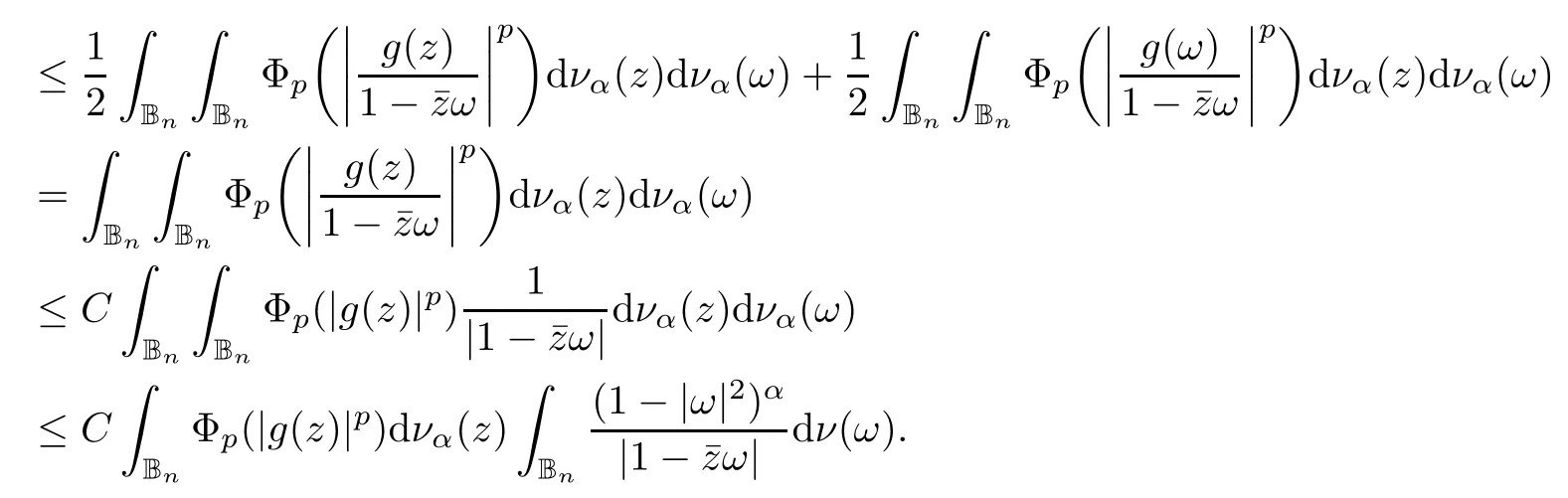
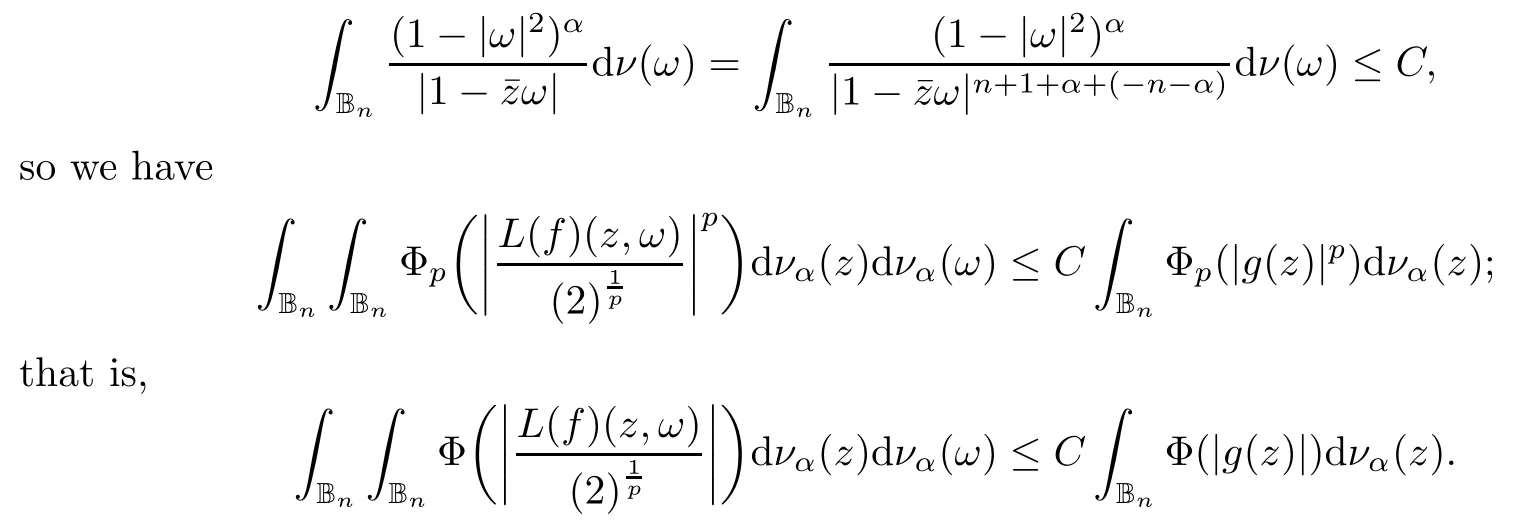


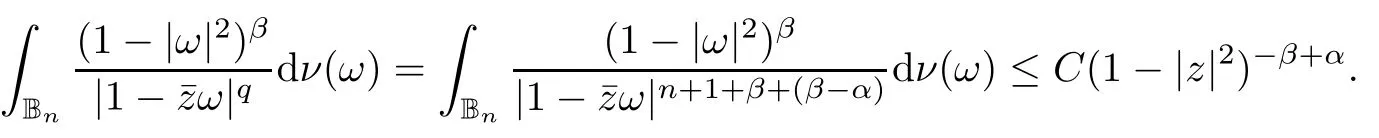



 Acta Mathematica Scientia(English Series)2020年5期
Acta Mathematica Scientia(English Series)2020年5期
