THE DAVIES METHOD FOR HEAT KERNEL UPPER BOUNDS OF NON-LOCAL DIRICHLET FORMS ON ULTRA-METRIC SPACES?
Jin GAO (高晉)
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China
E-mail : gao-j17@mails.tsinghua.edu.cn

where j is a symmetric Radon measure on (M ×M) diag. For simplicity, we denote E(f,f)by E(f). We need to specify the domain of E. Let D be the space defined by
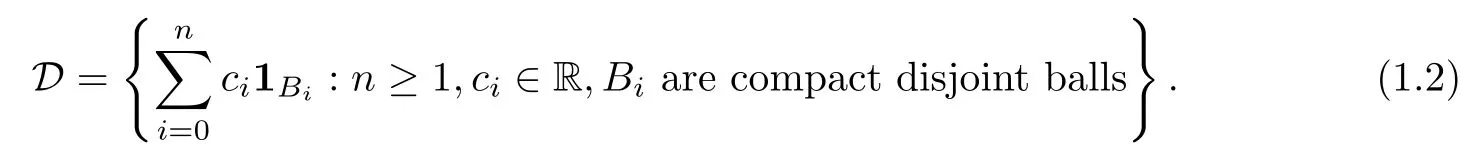
Let the space F be determined by
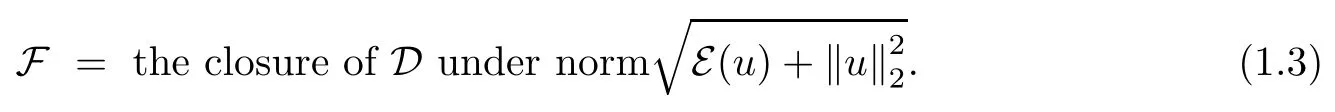
Then (E,F) is a regular Dirichlet form in L2:= L2(M,μ) if the measure j satisfies that j(B,Bc)<∞for any ball B (see [2, Theorem 2.2]).
Recall that the indicator function 1Bfor any ball B belongs to the space F if j(B,Bc)<∞,because
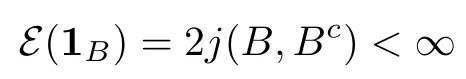
(see [2, formula (4.1)]).
In the sequel,we will fix some numbers α >0 and β >0,and some value R0∈ (0,diam M],which contains the case when R0= diam M = ∞. The letter C is universal positive constant which may vary at each occurrence.
We list some conditions to be used later on.
? Condition(TJ): there exists a transition function J(x,dy) such that
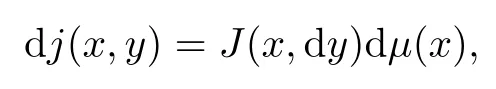
and for any ball B :=B(x,r) with x ∈ M and r ∈ (0,R0),
? Condition(DUE): the heat kernel pt(x,y) exists and satisfies
? Condition(wUE): the heat kernel ptexists and satisfies
Our aim in this article is to obtain the following:
Theorem 1.1Let(E,F)be given by(1.1),(1.3)on an ultra-metric measure space. Then

The result (1.4) is not new (see [2, Lemma 5.2, Theorem 12.1 and Subsection 12.3]), and was proved in [2, Theorem 2.8]by using a very complicated idea that was developed in several articles[7–11](After this article was finished, we became aware of the fact that a much simpler proof was recently presented in [2]). What is new in this article is that we apply the Davies method developed in [3, 5](see also [13, 14], [12, p1152]on general metric measure spaces including fractals) to give a much simpler proof for the implication (1.4). The key observation here is that the heat kernel for the truncated Dirichlet form vanishes at any time when points are separated by a ball of a radius larger than the truncated range (see Lemma 2.7 below).This new phenomenon arises from the ultra-metric property of the space M (General metric spaces do not admit this nice property). It would be interesting to generalize Theorem 1.1 by using the Davies method to the more general case when the condition (DUE) becomes
where φ is an increasing function on [0,∞), and V(x,r)= μ(B(x,r)) is the volume of the ball B(x,r) that is also sensitive to the center x.
2 Heat Kernel for the Truncated Dirichlet Form
We need to consider the truncated form and then estimate the corresponding heat kernel.We will do this by using the Davies method.
For any ρ >0, let E(ρ)be defined by
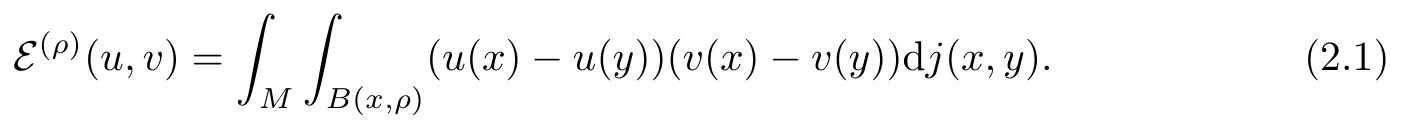
It is known that if
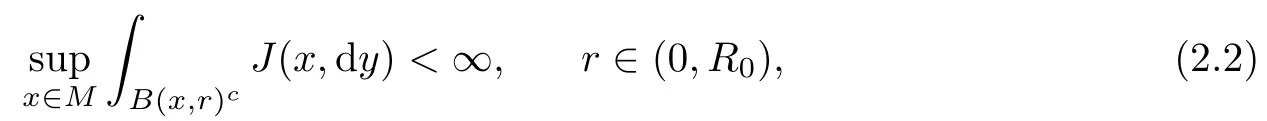
then E(ρ),F is closable and its closure form E(ρ),F(ρ)is a regular Dirichlet form (see [10,Proposition 4.2]). Condition (TJ) implies condition (2.2), so it also implies that the form(E(ρ),F(ρ)) is regular (see [2, Theorem 2.2]).
Proposition 2.1If conditions(TJ),(DUE)hold,then the following functional inequality(called Nash inequality) holds: there exists a constant CN> 0 (subscript N means that this constant comes from “Nash” inequality) such that, for any u ∈ F ∩ L1,
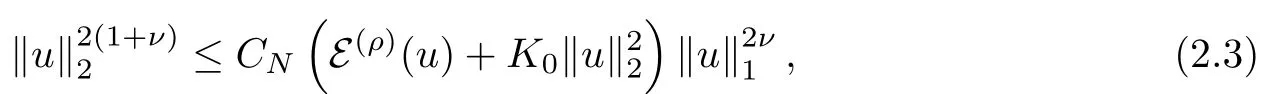
where ν :=β/α and K0:=ρ?β+R?β0.
ProofAs (DUE) holds, we have, by [3, Theorem (2.1)], that
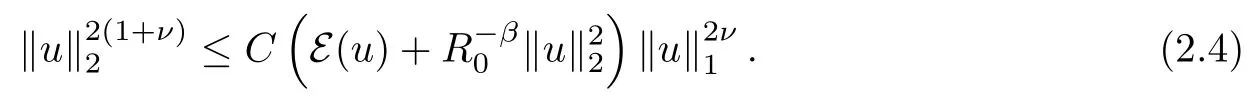
On the other hand, by condition (TJ) and the symmetry of j, we have
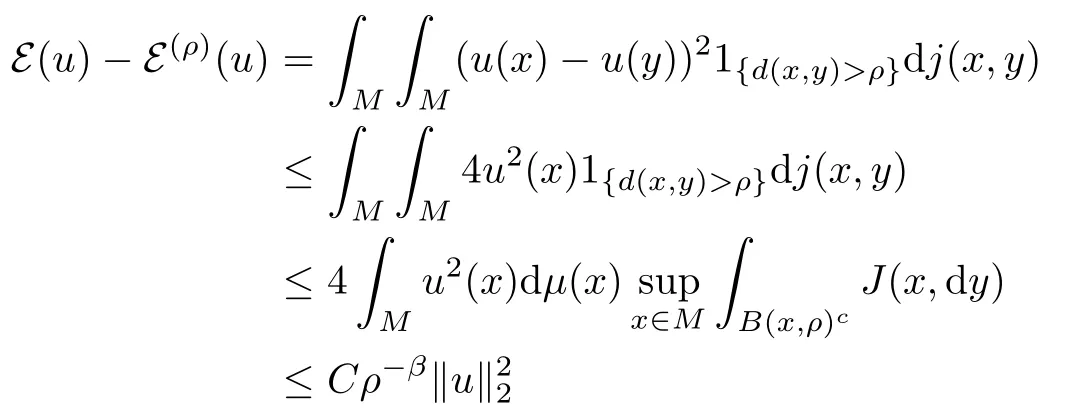
(note, by this inequality, that F(ρ)=F). Plugging this into (2.4), we obtain (2.3).
We now need the following:
Proposition 2.2Let B be any ball of radius r >0. If 0< ρ ≤ r, then

for any f,g ∈ F(ρ)∩ L∞, where ψ = λ1Bwith λ ∈ R.
ProofAs ψ = λ1B∈ F, we see that eψ? 1 ∈ F(ρ)∩ L∞, by using the Markov property of (E(ρ),F(ρ)), and hence both functions eψg and e?ψg belong to F(ρ)∩ L∞if g ∈ F(ρ)∩ L∞.
As 0< ρ ≤ r, we see that B(x,ρ) ? B(x,r)=B if x ∈ B, whereas B(x,ρ)? Bcif x ∈ Bc,because two balls B(x,ρ) and B are disjoint by using the ultra-metric property. Thus
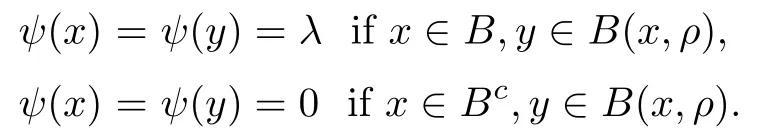
It follows that
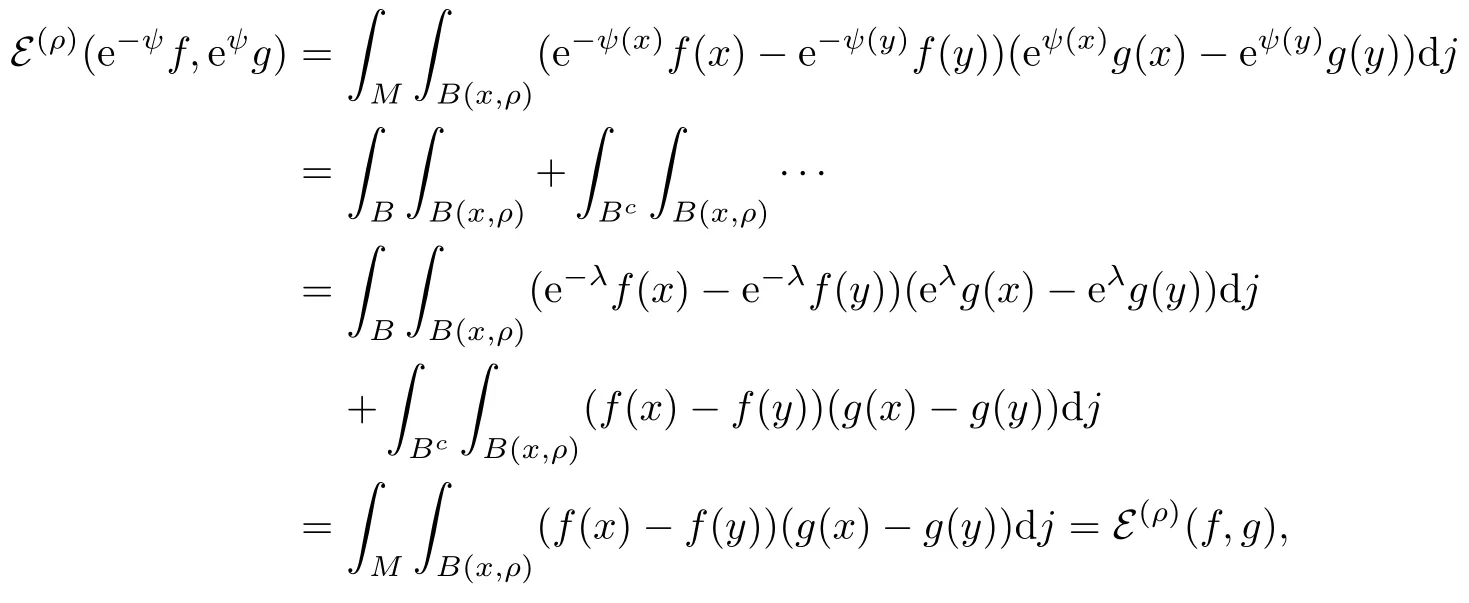
thus proving (2.5).
Corollary 2.3Let B be any ball of radius r >0. If 0< ρ ≤ r, then
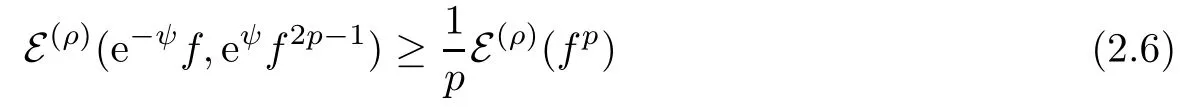
for any f ∈ F(ρ)∩ L∞and any p ≥ 1, where ψ = λ1Bwith λ ∈ R.
ProofUsing the elementary inequality
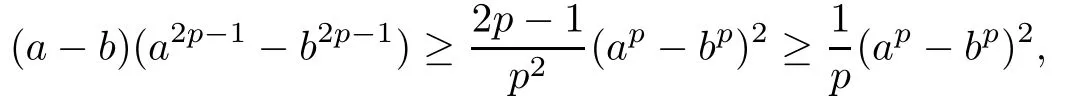
for any non-negative numbers a,b and any p ≥ 1, and taking g =f2p?1for any p ≥ 1 in (2.5),we obtain, by letting a=f(x),b=f(y), that
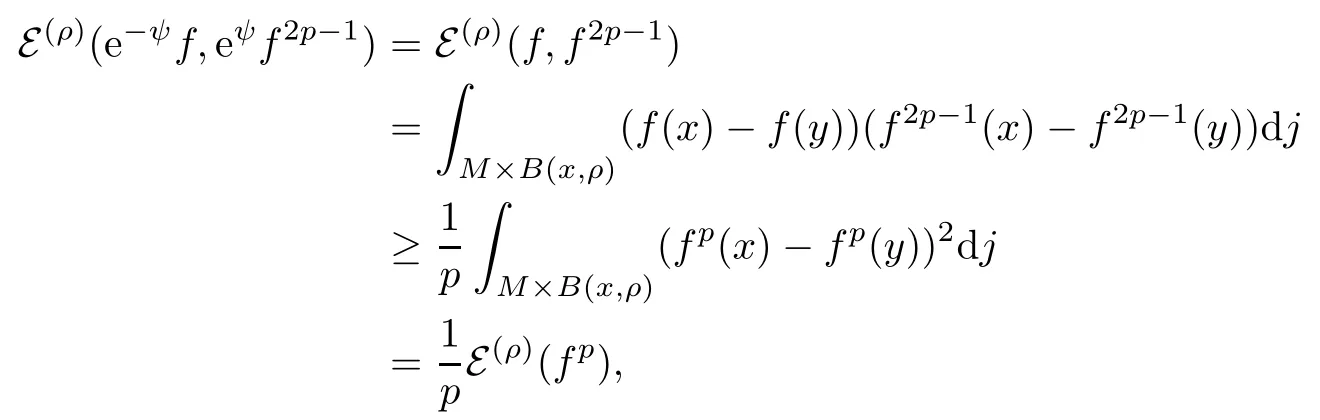
thus proving (2.6).
Remark 2.4Inequality (2.6) is an enhancement of the previous similar results in [3,formula (3.11)]and [13, formula(2.8)](see also [12, formula (3.11)])in the setting of the ultrametric space.
For any f ∈ F ∩ L∞with f2=1, denote by {Qt}t≥0the heat semigroup of (E(ρ),F(ρ)).Let

be the perturbed semigroup of {Qt}t≥0.
Proposition 2.5Let B be any ball of radius r >0. If 0< ρ ≤ r, then
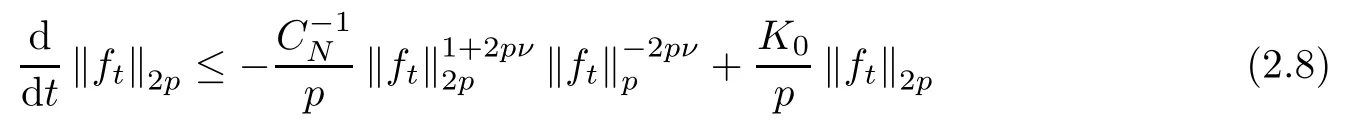
for any non-negative ft∈ F(ρ)∩ L∞and any p ≥ 1, where ψ = λ1Bwith λ ∈ R as before, and CNis the same as in (2.3).
ProofNote that ft∈ F(ρ)∩ L∞. Then, using (2.6) with f being replaced by ft,
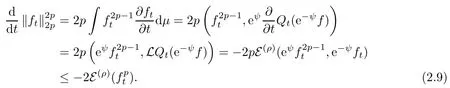
On the other hand, applying the Nash inequality(2.3)with u being replaced bywe see that
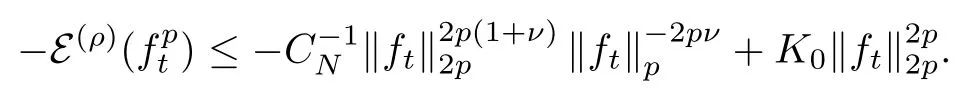
Plugging this into (2.9), we obtain

which gives (2.8) after dividingon both sides.
For any integer k ≥1, we define the function wk(t) for t>0 by
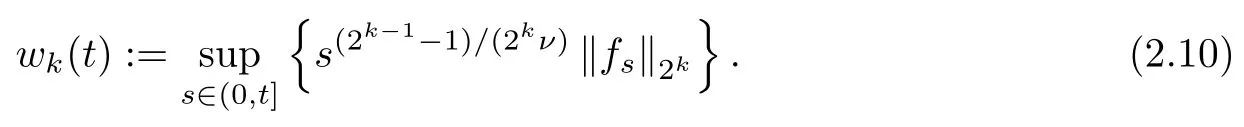
Clearly, wk(t) is non-decreasing in t>0. Note that, by (2.8) with p=1,
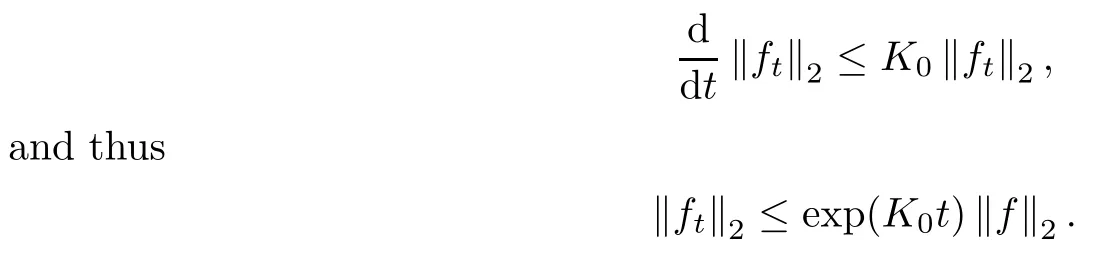
This gives that for any t>0,
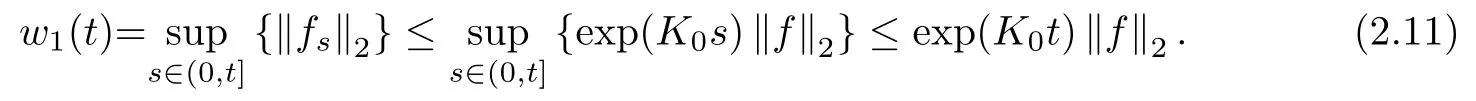
We will estimate wkby iteration.
Proposition 2.6Let wkbe defined as in(2.10). Then for any non-negative f ∈ F(ρ)∩L∞,
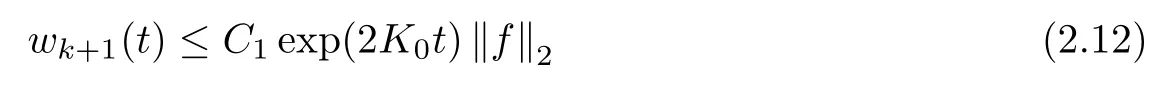
for any t >0, where C1is some universal constant depending only on ν,CN(but independent of t,ρ,r and λ), andas before.
ProofFor any integer k ≥1, denote
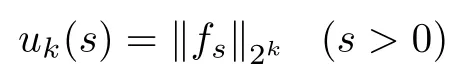
for simplicity. Applying (2.8) with p=2k, we have
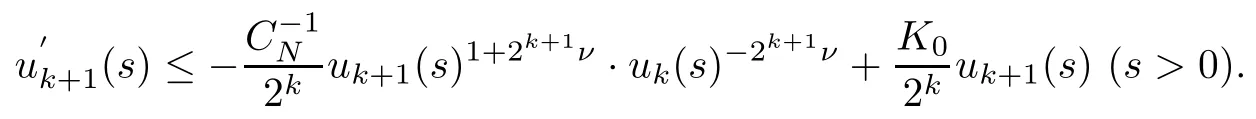
As wk(s)≥ s(2k?1?1)/(2kν)uk(s), by definition (2.10), we obtain
Applying Proposition A1 in Appendix with u(s)=uk+1(s),θ =2k+1ν and b=p=2k,w =wk, and K =K02?k,a=1, we obtain
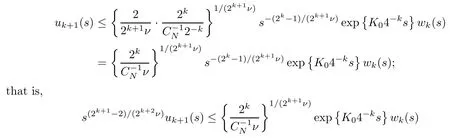
for any s>0.
Therefore, for any t>0,k >0,
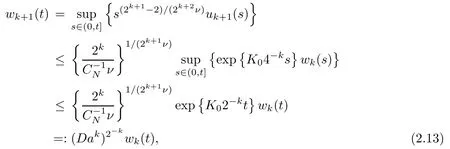
By iteration, we see from (2.13) and (2.11) that for any k ≥1,
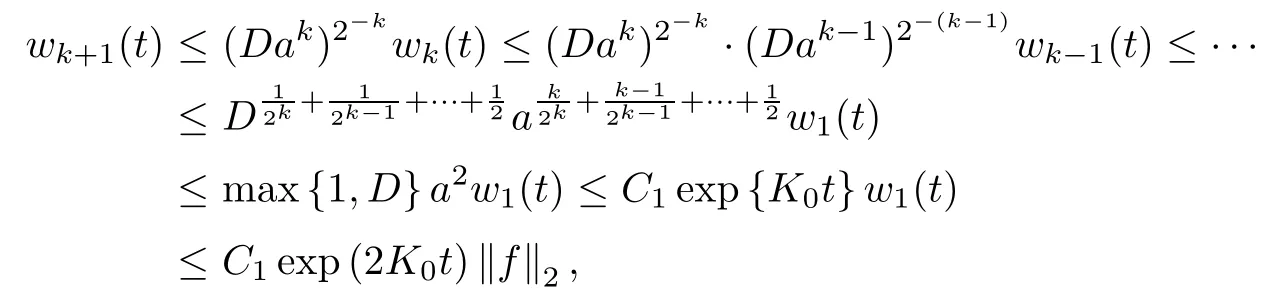
where C1=thus proving (2.12).
We now estimate the heat kernelof the truncated Dirichlet form (E(ρ),F(ρ)).
Lemma 2.7Assume that conditions (TJ), (DUE) hold. Then, for any ball B of radius r ∈ (0,R0) and for any 0< ρ ≤ r, the heat kernelof (E(ρ),F(ρ)) exists and satisfies

for μ-almost all x ∈ B,y ∈ Bcand for all t>0.
ProofLet 0 ≤ f ∈ F ∩ L∞with f2=1. By (2.12), we have
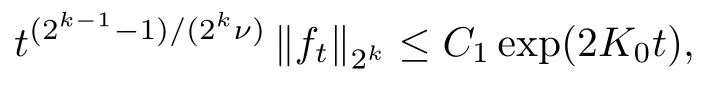
which gives, by letting k → ∞, that
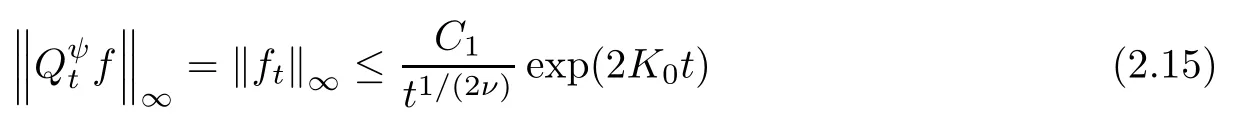
for any t>0. It follows that
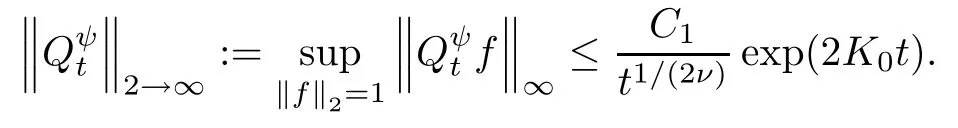
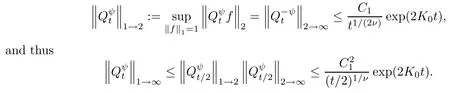
From this, we conclude that the heat kernelof (E(ρ),F(ρ)) exists and satisfies
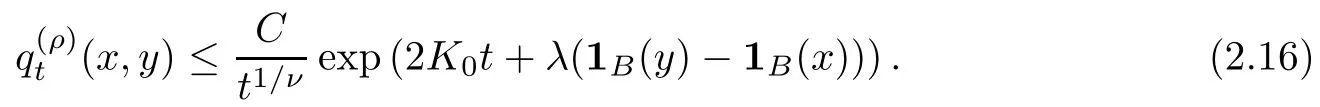
Therefore, for μ-almost all x ∈ B,y ∈ Bcand for all t>0,
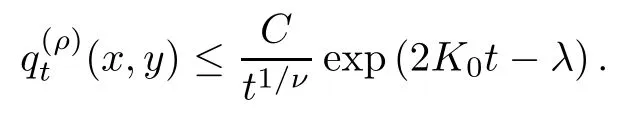
Lemma 2.7 says that the heat kernelof the truncated Dirichlet form will vanish for any t>0 when points x and y are separated by any ball of radius r >ρ. This means that the Hunt process associated with the truncated Dirichlet form never goes farther away than the truncated range ρ. This lemma will give the strong tail estimate of the heat semigroup {Pt}of the form (E,F). This new phenomenon arises from the ultra-metric property of the space M. General metric spaces do not admit this nice property. For example, for δ ∈ (0,1), the Dirichlet form(Eδ,Fδ)is regular on Rd(see[4,(2.14)–(2.16)]). Let Zδbe a symmetric Markov process associated with (Eδ,Fδ). The generator of Zδis
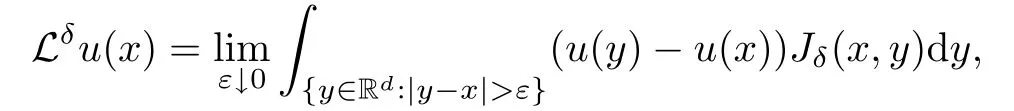
where Jδ(x,y) is a symmetric non-negative function (see [4, (3.4)]). Zδhas a quasi-continuous heat kerneldefined on [0,+∞)× Rd× Rd. For δ0>0, there exist c=c(δ0)>0 such that≥ ct?d/2for every t > δ0and quasi everywhere x,y with |x ? y|2≤ t (see [4,Theorem 3.4]).
Proposition 2.8Assume that conditions (TJ), (DUE) hold. Then, for any ball B of radius r ∈(0,R0) and for any t>0,

for some universal constant C >0 (independent of t,B).
ProofBy Lemma 2.7, we have that for μ-almost all x ∈ B and all t>0,
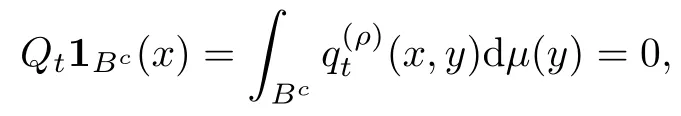
if 0< ρ ≤ r. Applying Proposition A2in Appendix for? =M,f =1Bc, we see that
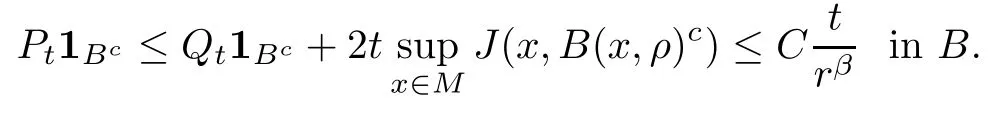
The proof is complete.
We are in a position to prove Theorem 1.1.
ProofFix points x0,y0∈M and fix t ∈Without loss of generality,assume thatotherwise (wUE) follows directly from (DUE) and nothing is proved. Let r =Noting that Pt1Bcis monotone decreasing in r, we have from (2.17), for r >0,t>0,that

It follows from condition (DUE) and (2.18), forμ-almost all x ∈ B(x0,r),y ∈ B(y0,r), that we have
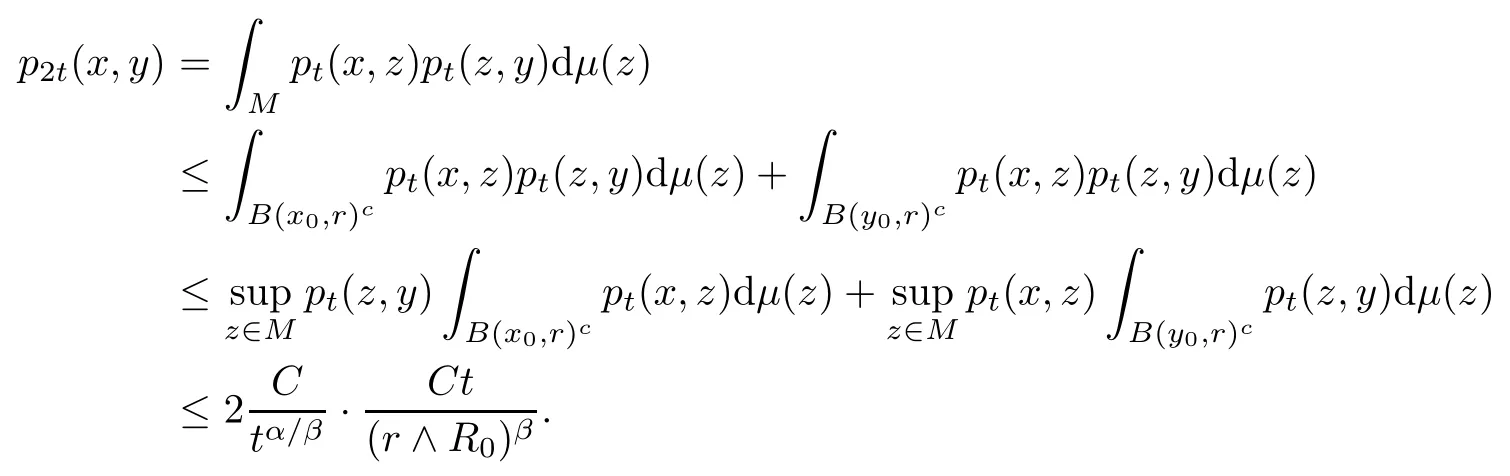
Therefore, for μ-almost all x0,y0∈M and t ∈we conclude that
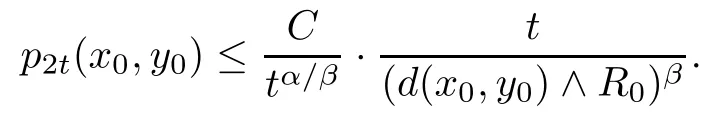
This inequality, together with (DUE), will imply (wUE). The proof is complete.
AcknowledgementsThe author thanks Jiaxin Hu and Alexander Grigor’yan for suggesting this topic, and Eryan Hu for discussions.
Appendix
The following was first shown in [3, Lemma 3.21], and then was modified in [13, Lemma 2.6](see also [12, Lemma 3.4]):
Proposition A1Let w:(0,∞)→ (0,∞)be a non-decreasing function and suppose that u ∈ C1([0,∞);(0,∞)) satisfies that for all t ≥ 0,
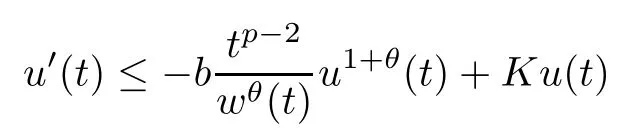
for some b>0, p>1, θ >0 and K >0. Then
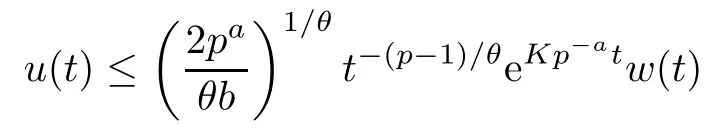
for any a ≥1.
The following result was proved in [10, Proposition 4.6]:
Proposition A2For an open set ? ? M, letbe the heat semigroups of (E,F(?)) andrespectively. Then, for any t>0,
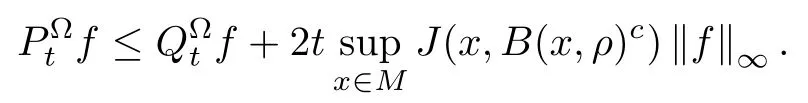
 Acta Mathematica Scientia(English Series)2020年5期
Acta Mathematica Scientia(English Series)2020年5期
- Acta Mathematica Scientia(English Series)的其它文章
- RETRACTION NOTE: “MINIMAL PERIOD SYMMETRIC SOLUTIONS FOR SOME HAMILTONIAN SYSTEMS VIA THE NEHARI MANIFOLD METHOD”Acta Mathematica Scientia, 2020,40B(4):614–624
- DYNAMIC ANALYSIS AND OPTIMAL CONTROL OF A FRACTIONAL ORDER SINGULAR LESLIE-GOWER PREY-PREDATOR MODEL?
- POSITIVE SOLUTIONS AND INFINITELY MANY SOLUTIONS FOR A WEAKLY COUPLED SYSTEM?
- PARAMETERS IDENTIFICATION IN A SALTWATER INTRUSION PROBLEM?
- A LEAST SQUARE BASED WEAK GALERKIN FINITE ELEMENT METHOD FOR SECOND ORDER ELLIPTIC EQUATIONS IN NON-DIVERGENCE FORM?
- EXISTENCE AND CONCENTRATION BEHAVIOR OF GROUND STATE SOLUTIONS FOR A CLASS OF GENERALIZED QUASILINEAR SCHRDINGER EQUATIONS IN RN?
