一道教師解題能力展示試題的賞析
廣東佛山順德羅定邦中學(528300) 李定平
1 題目
2018 佛山青年教師解題能力展示試題第16 題:設函數(shù)f(x)=?x2+bx+|x ?a|?a ?1,(a,b ∈R),若對?a ∈R,函數(shù)f(x)至多有兩個不同的零點,則b的取值范圍是____.
姑且不論難易得分如何? 此題中既是分段函數(shù),又含有兩個參數(shù)a和b,而且還有對任意參數(shù)a命題成立求參數(shù)b范圍的恒成立問題,是一個綜合性較強的題,引起筆者的探索.
2 解法呈現(xiàn)
思維視角1討論f(x)的單調(diào)區(qū)間,由零點個數(shù)確定的區(qū)間端點的正負求b范圍.
解法1等價于對?a ∈R,f(x) =x2?bx ?|x ?a|+至多有兩個不同的零點,而f(x)是兩個開口向上,對稱軸分別為和的分段二次函數(shù).


圖1

圖2

圖3
思維視角2函數(shù)零點轉(zhuǎn)化為二次函數(shù)與分段函數(shù)的交點,由分段交點個數(shù)求b范圍
解法2等價于對?a ∈R,關(guān)于x的方程

至多有兩個不同的解, 即h(x) =x2?bx g(x) =至多有兩個不同的的交點,而g(x)的圖像是頂點為P(a,?a ?1),斜率分別為1 和?1 的折線,其中左側(cè)是l:y=?x ?1,右側(cè)是m:y=x ?2a ?1.
當l與h(x)無交點時, 即x2?(b ?1)x+1 = 0 無實數(shù)解,即?= (b ?1)2?4<0 得:?1< b <3 時,右折線m:y=x ?2a ?1 與h(x)最多兩交點,方程1○至多有兩個不同的解;
當l與h(x) 有一個交點, 即b= 3 或b= 1 時, 右折線m與h(x)可能存在兩個交點,如b= 3 時,當a= 0 時,x2?3x=x ?2a ?1 存在兩個大于a的解,方程1○有三解,不滿足要求.
當l與h(x)有兩個交點時(如圖3),作h(x)的斜率為1 的切線n, 記切點為A, 若A在直線l的上方時, 存在右折線m也與h(x)有兩個不同交點,故g(x)與h(x)有4 交點,方程1○有4 解,不滿足要求; 若A在直線l的下方或在直線l上時,g(x)與h(x)至多有2 交點,滿足要求,設切線n:y=x+c,代入y=x2?bx得:x2?(b+1)x ?c= 0,所以即b2?2b ?7 ≥0,解得或此時滿足要求.
綜上所述,略.
思維視角3函數(shù)零點轉(zhuǎn)化為一個含參數(shù)a的函數(shù)與參數(shù)b表示常數(shù)函數(shù)的交點,由交點個數(shù)求b范圍
解法3等價于對?a ∈R,關(guān)于x的方程
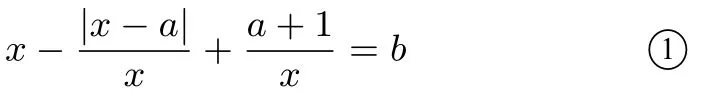
至多有兩個不同的解,即等價于h(x) =與y=b至多有兩個不同的的交點, 而p(x) =x ?1 +, 當2a+ 1>0 時與一樣是對鉤函數(shù), 當2a+ 1<0 時是(?∞,0)與(0,+∞)都單增的兩段增函數(shù).
(1)當a≤?1 時,q(x)在(?∞,a]上單增,p(x)在(a,0)上單增,在(0,+∞)上單增,h(x)與y=b至多有兩個不同的的交點,則b ∈R(如圖4);
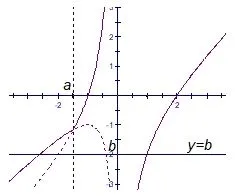
圖4

圖5

圖6
因為對?a ∈R,至多只有兩個交點,所以上述所求b范圍取交集即為所求.
評析這種化歸觀察交點個數(shù)最為明顯.
思維視角4求補集:?a ∈R,f(x)至少有三個不同的零點,求b的取值范圍.
解法4由h(x) =x2?(b ?1)x+1(x≤a)有兩零點x1 由g(x) =x2?(b+ 1)x+ 2a+ 1(x > a) 有兩零點a ?a ∈使式成立,即 ?a ∈使式成立,即 評析注意“?a ∈使式成立”的運算. 思維視角5求補集:化歸為?a ∈R,含參數(shù)b的拋物線與含參數(shù)a的折線至少有三個不同的交點,求b的取值范圍. 圖7 解法5由f(x) = 0 變形為x2?bx=|x ?a|?a ?1,令h(x) =x2?bx,g(x) =|x ?a|?a ?1,h(x)與g(x)至少有三個交點(如圖7),則h(a)≥g(a),即 評析V 型折線與拋物線至少有三個交點當且僅當V 型頂點在兩切點之間且在拋物線下方,兩切點在折線下方. 函數(shù)的零點可轉(zhuǎn)化為兩函數(shù)的交點,對?a ∈R,則要想象參數(shù)a任意變化,相應的函數(shù)圖象如何變化,對直觀想象能力要求較高,分界點x=a變化導致函數(shù)圖形變化主要靠想象,不僅優(yōu)秀學生需要這樣的訓練,作為教師也需要. 函數(shù)零點問題大部分是含一個參數(shù),象這樣含兩個參數(shù)的題較少,如2015 湖南卷理第15 題:已知f(x)=若存在實數(shù)b,使函數(shù)g(x) =f(x)?b有兩個零點,則a的取值范圍是____.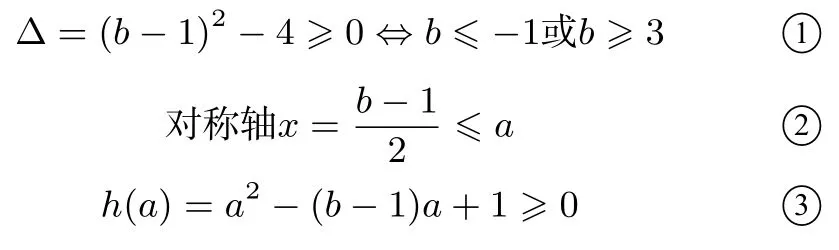


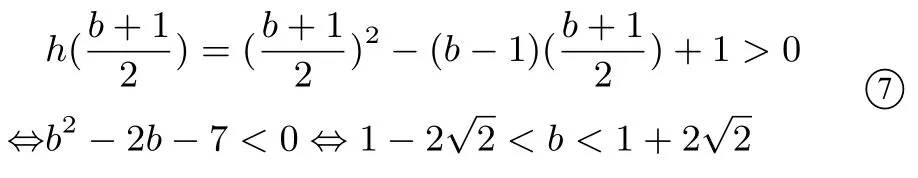
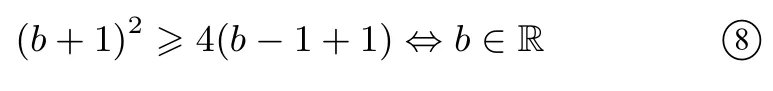


3 感想

