天津市耀華中學(xué)(300040) 明廷軍

圖形的變化是初中平面幾何中非常重要的內(nèi)容,它不僅有助于發(fā)展學(xué)生的識圖能力,培養(yǎng)學(xué)生的幾何直觀感覺,也有助于學(xué)生分類討論思想的形成. 因此,在全國各地的數(shù)學(xué)中考試題中,與“圖形的變化”相關(guān)的問題幾乎都以壓軸題的形式出現(xiàn). 因此如何在動態(tài)的過程中進行觀察、想象與分析,進而去化解“圖形的變化”中所遇到的問題,在我們的平面幾何學(xué)習(xí)中顯得尤為重要. 本文嘗試著利用微課教學(xué)從實例剖析的角度去引導(dǎo)學(xué)生對“圖形變化”中的平移問題進行探討,進而培養(yǎng)學(xué)生的圖形想象能力與邏輯推理能力.

1 在平移過程中認識圖形的變化

圖形在平移的過程中往往呈現(xiàn)變化多樣性的特點,對變化多樣性的理解程度直接影響著我們對問題的判斷,所以認識圖形在平移過程中所經(jīng)歷的每一個狀態(tài)是解決問題的關(guān)鍵. 在微課教學(xué)中利用多媒體可以高效直觀地解決這個問題.

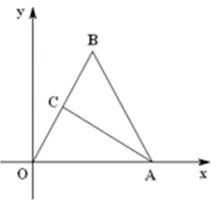
例1在平面直角坐標系中,O為原點, 點A(6,0), 點B在y軸的正半軸上,∠ABO=30°. 矩形CODE的頂點D,E,C分別在OA,AB,OB上,OD=2.

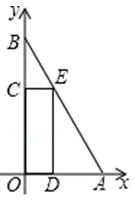
圖1

(Ⅰ)如圖1,求點E的坐標;

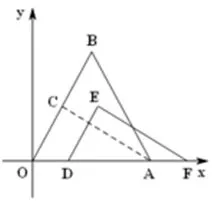
(Ⅱ) 將矩形CODE沿x軸向右平移,得到矩形C′O′D′E′, 點C,O,D,E的對應(yīng)點分別為C′,O′,D′,E′. 設(shè)OO′=t, 矩形C′O′D′E′與?ABO重疊部分的面積為S.

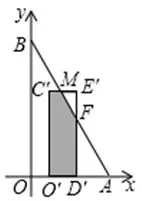
圖2

(Ⅰ)如圖2,當矩形C′O′D′E′與?ABO重疊部分為五邊形時,C′E′,E′D′分別與AB相交于點M,F, 試用含有t的式子表示S, 并直接寫出t的取值范圍;

評注:這道題是天津市2019年中考試卷的第24 題,在這道題中,如果能認識到矩形CODE沿x軸向右平移的過程中,重疊部分的形狀會經(jīng)歷五邊形、四邊形和三角形這樣三種狀態(tài),而且重疊部分的面積會越來越小,那么這道題就能被我們輕松地解決.

2 在平移過程中關(guān)注圖形的不變性

在圖形的平移過程中,只改變圖形的位置,不改變圖形的大小和形狀. 圖形平移的這一特點為我們認識復(fù)雜圖形提供了很大幫助,大大提升了我們解決問題的能力. 在微課教學(xué)中多媒體動畫的使用可以幫助我們強化這一認知.

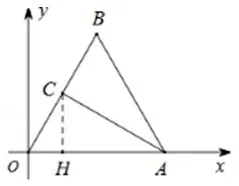
例2在平面直角坐標系中,點A(4,0),B為第一象限內(nèi)一點,且OB⊥AB,OB=2.

(Ⅰ)如圖5,求點B的坐標;

(Ⅱ)如圖6,將?OAB沿x軸向右平移得到?O′A′B′,設(shè)OO′=m,其中0< m <4,連接BO′,AB與O′B′交于點C.

(Ⅰ)試用含m的式子表示?BCO′的面積S,并求出S的最大值;

(ⅱ)當?BCO′為等腰三角形時,求點C的坐標(直接寫出結(jié)果即可).

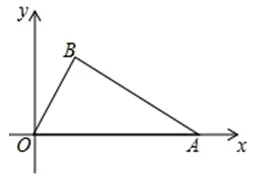
圖5

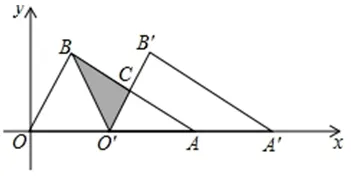
圖6

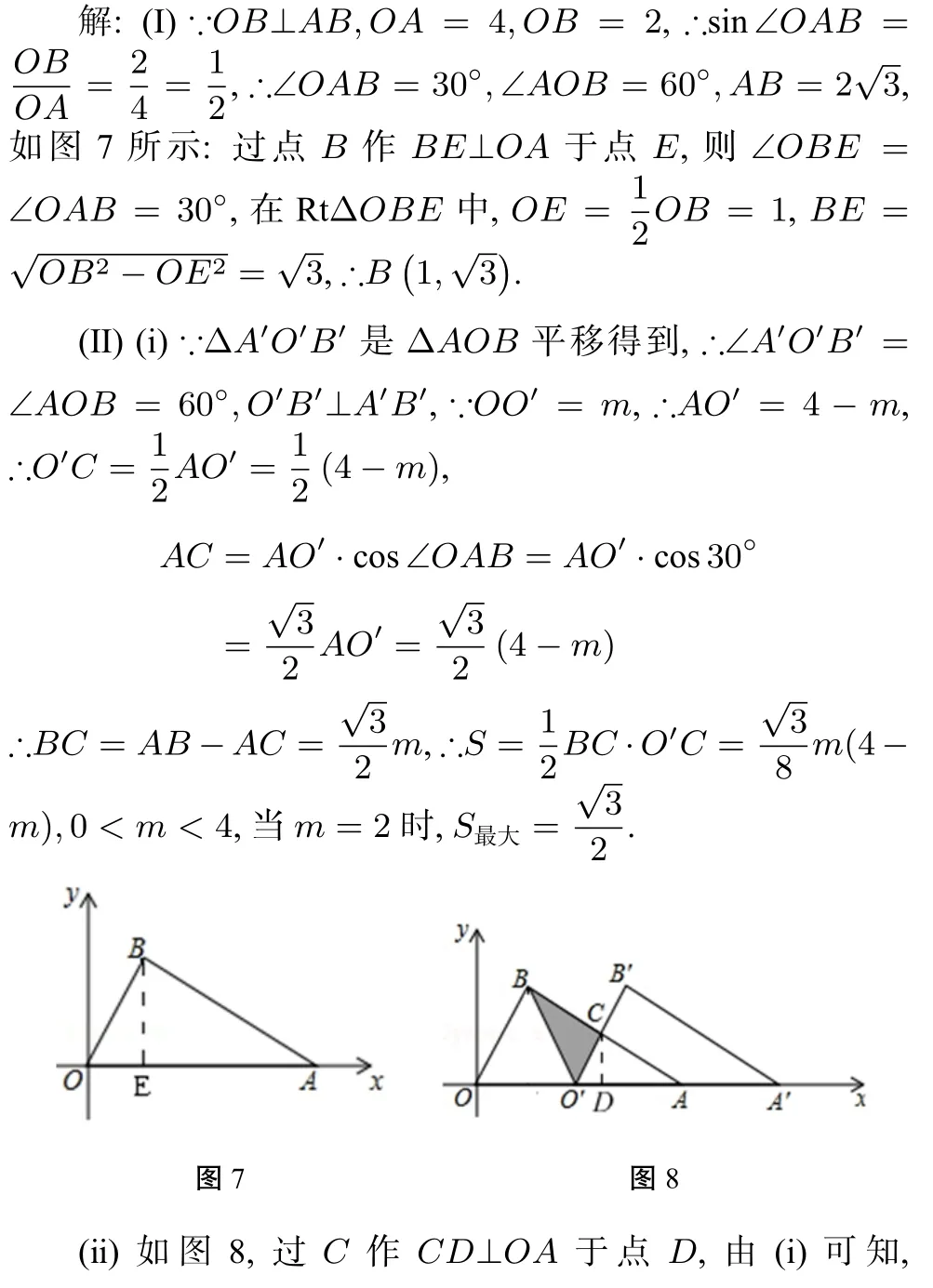
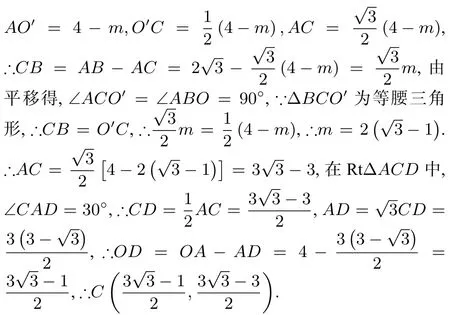
評注:在這道題中, 如果能注意到在?OAB的平移過程中,始終有∠A′O′B′= ∠AOB,且O′B′//OB,進而發(fā)現(xiàn)∠ACO′=90°,那么我們就能很容易地找到解題的突破口.

3 在平移過程中探究最值問題

在圖形的平移過程中, 有些隱含的元素是始終相等的,如果能從中發(fā)現(xiàn)圖形的這些隱含元素, 并合理地加以運用,進而將復(fù)雜陌生的問題化作簡單熟悉的問題,那么我們的數(shù)學(xué)能力一定會在圖形的不斷變化中得到培養(yǎng),我們的思路也會變得更加開闊. 依托于多媒體的微課教學(xué)為這種圖形變化提供了可能.

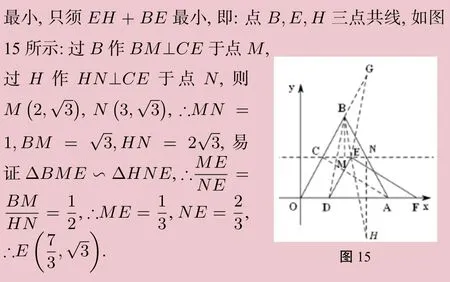
例3在平面直角坐標系中,點A(4,0),B為第一象限內(nèi)一點,且?OAB為等邊三角形,C為OB的中點,連接AC.

(Ⅰ)如圖9,求點C的坐標;

(Ⅱ) 如圖10, 將?OAC沿x軸向右平移得到?DFE,設(shè)OD=m,其中0

(Ⅰ)設(shè)?OAB與?DEF重疊部分的面積為S,用含m的式子表示S;

(ⅱ)連接BD,BE,當BD+BE取最小值時,求點E的坐標(直接寫出結(jié)果即可).

圖9

圖10

圖11

評注:在這道題中, 由于點D和點E都是動點, 所以BD+BE的最值不好分析,如果我們能發(fā)現(xiàn)EG其實就是DB沿著DE平移而來,因而它們的長度相等,再結(jié)合對稱的性質(zhì),我們就能把BD+BE轉(zhuǎn)化成EH+BE,即一個動點到兩個定點的距離之和,這樣“兩點之間,線段最短”就可以使用了.

在平面幾何的學(xué)習(xí)過程中,對于“圖形的變化”所涉及到的平移問題,我們?nèi)绻軠蚀_地認識平移過程中所經(jīng)歷的每一個狀態(tài),充分把握圖形平移過程中的不變性,努力挖掘圖形平移過程中所隱含的相等元素,那么很多問題往往都能迎刃而解. 微課教學(xué)恰恰為我們提供了所需的方法和途徑.

我們也可以看到,正是因為有了圖形的變化,才有了幾何的魅力. 也因此擴展了學(xué)生的探究思維,提高了學(xué)生的判斷力,養(yǎng)成了學(xué)生的圖形識別能力,為后續(xù)的幾何學(xué)習(xí)打下堅實的基礎(chǔ).