幾類非線性數(shù)學(xué)物理方程精確解的符號(hào)計(jì)算
周 凱, 楊 軍, 馬立媛, 沈守楓
(1.浙江工業(yè)大學(xué)應(yīng)用數(shù)學(xué)系,浙江杭州310023;2.上海交通大學(xué)數(shù)學(xué)系,上海200240)
§1 引 言
孤子理論的發(fā)展說明了構(gòu)造非線性數(shù)學(xué)物理方程精確解的重要性.例如,鐘型和扭結(jié)型孤子解可以用來分析和模擬流體,等離子體和彈性介質(zhì)中的波現(xiàn)象.近些年,由于符號(hào)計(jì)算軟件Mathematica,Maple和Matlab的完善,一系列數(shù)學(xué)機(jī)械化方法如Hirota雙線性方法,函數(shù)展開法,Painlev′e分析和Lie對(duì)稱方法得到了快速發(fā)展[1-13].
首先利用Hrota雙線性方法[14-16]考慮如下的可積非局部離散mKdV方程.
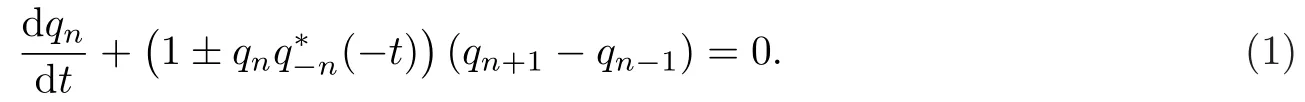
這里t∈R是連續(xù)變量,n∈N是離散變量,?表示復(fù)共軛.方程(1)擁有離散的矩陣譜問題
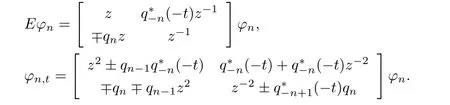
移位算子E定義為Ef(n)=f(n+1),Ef(?n)=f(?(n+1)).方程(1)可退化為非局部mKdV方程[17-18]
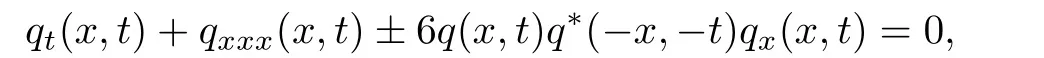
其次,利用Jacobi橢圓函數(shù)直接構(gòu)造如下的多分量Klein-Gordon方程
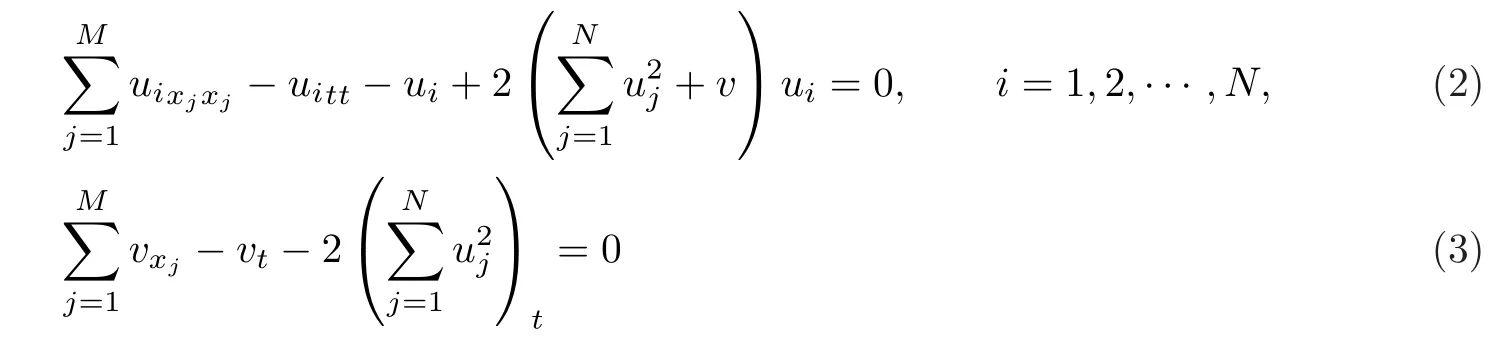
和多分量長(zhǎng)波-短波方程

的精確解.事實(shí)上,對(duì)于多分量方程來說,很少有其精確解成功構(gòu)造的工作.各種形式的Klein-Gordon方程可以用來研究淺水波,光纖通訊和量子物理[19-24].特別地,當(dāng)M=1時(shí),文獻(xiàn)[25]給出了Painlev′e分析.對(duì)于長(zhǎng)波-短波方程,文獻(xiàn)[26]利用Hirota雙線性方法給出了線孤子解.
文章的安排如下:利用Hirota雙線性方法,§2給出了方程(1)的N-孤子解的顯式表達(dá)式.特別地,分析了2-孤子解的漸近行為.§3利用Jacobi橢圓函數(shù)展開法給出了方程(2)-(3)和方程(4)-(5)的行波解.§4是文章的結(jié)論.
§2 方程(1)的2-孤子解和漸近行為
考慮到1-孤子解的表達(dá)式較為簡(jiǎn)單,將以注記的形式給出,所以直接構(gòu)造2-孤子解.首先引入Hirota雙線性算子
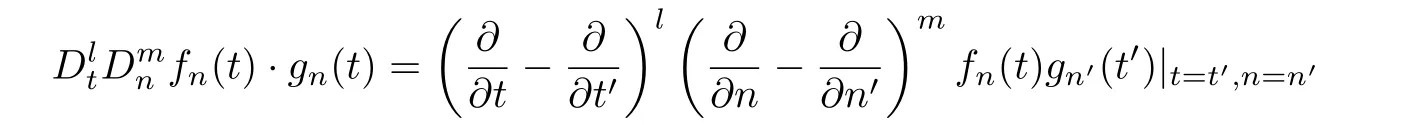
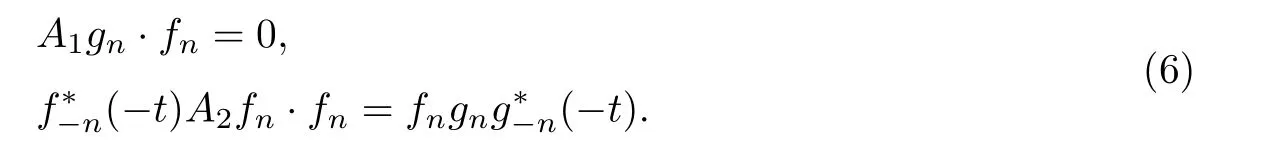
這里雙線性算子A1和A2由

及
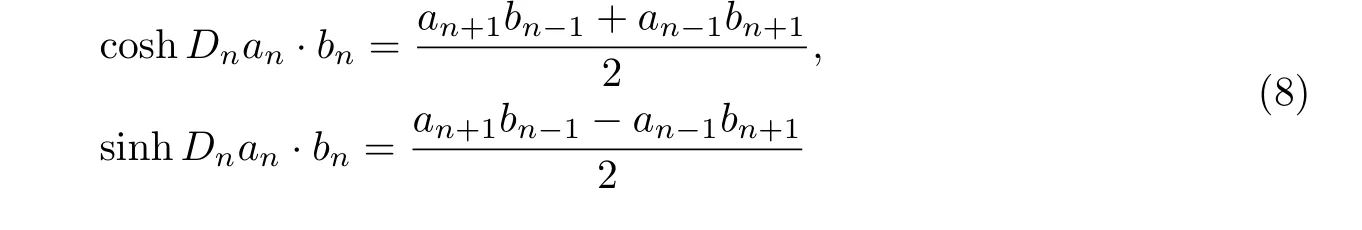
給出.

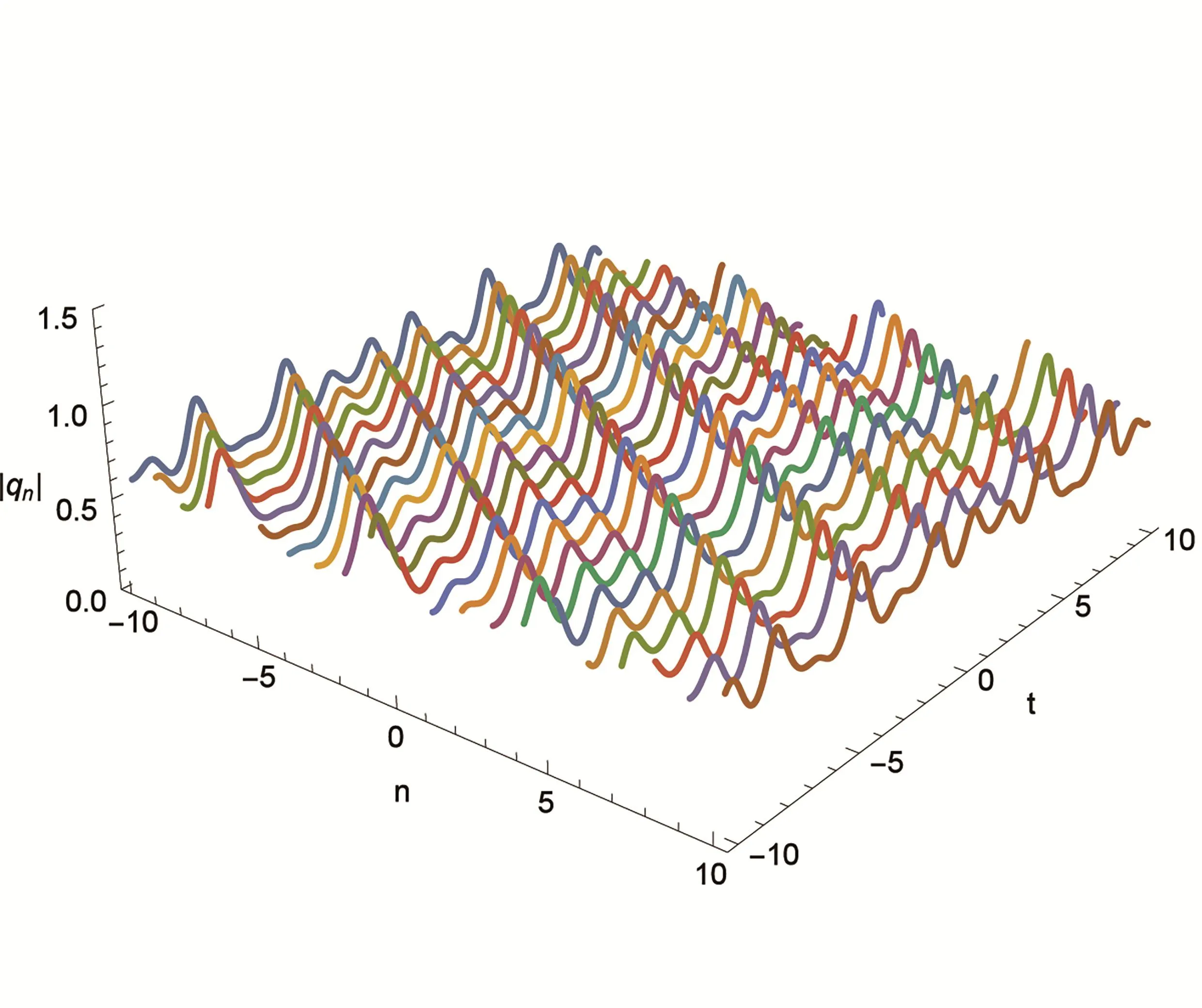
圖1 參數(shù)取k1=3i,k2=2i的2-孤子解
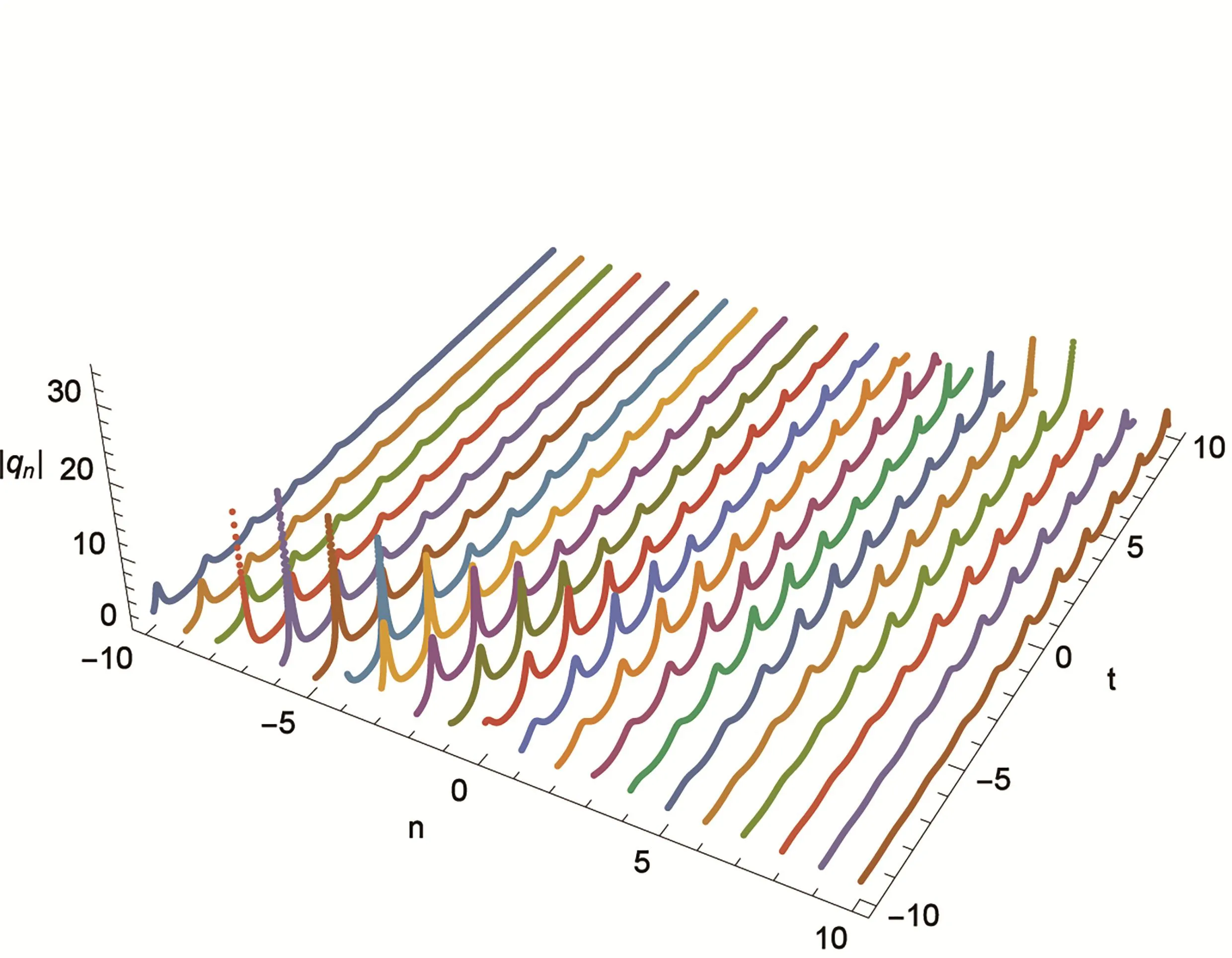
圖2 參數(shù)取k1=0.2+i,k2=i的2-孤子解
進(jìn)而對(duì)于其它方程,可知恒成立.
最后令ε=1,2-孤子解為
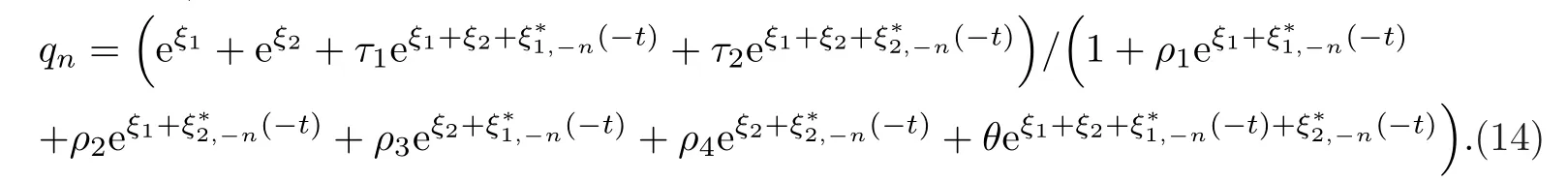
簡(jiǎn)便起見,這里記τ1=a(1,2,1?),τ2=a(1,2,2?),ρ1=a(1,1?),ρ2=a(1,2?),ρ3=a(2,1?),ρ4=a(2,2?),ρ5=a(1,2)和θ=a(1,2,1?,2?). 當(dāng)
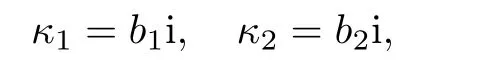
該2-孤子解(14)表現(xiàn)為保持彈性碰撞的周期孤子,見圖1.
如果選擇

則2-孤子解(14)的動(dòng)力學(xué)行為見圖2.
當(dāng)固定ξ1,可得
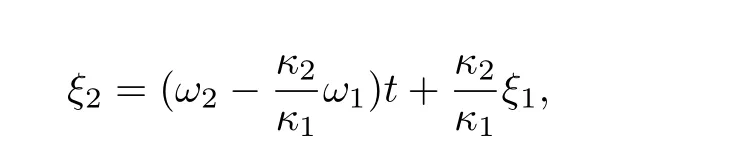

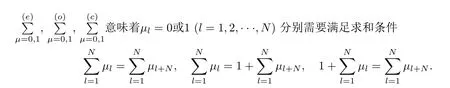
利用符號(hào)計(jì)算軟件Maple,可以構(gòu)造該精確解的相互作用行為.
§3 方程(2)-(3)的Jacobi橢圓函數(shù)解
設(shè)方程(2)-(3)的行波解為如下形式,

分別是模為m∈(0,1)的Jacobi橢圓正弦函數(shù),Jacobi橢圓余弦函數(shù)和第三類Jacobi橢圓函數(shù).這些Jacobi橢圓函數(shù)有如下的平方關(guān)系式
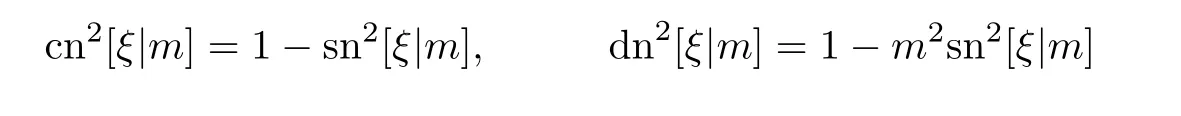
和導(dǎo)數(shù)關(guān)系式
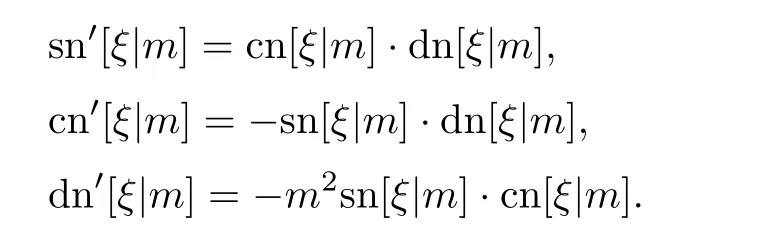
這樣可以分三種情形直接求解方程:
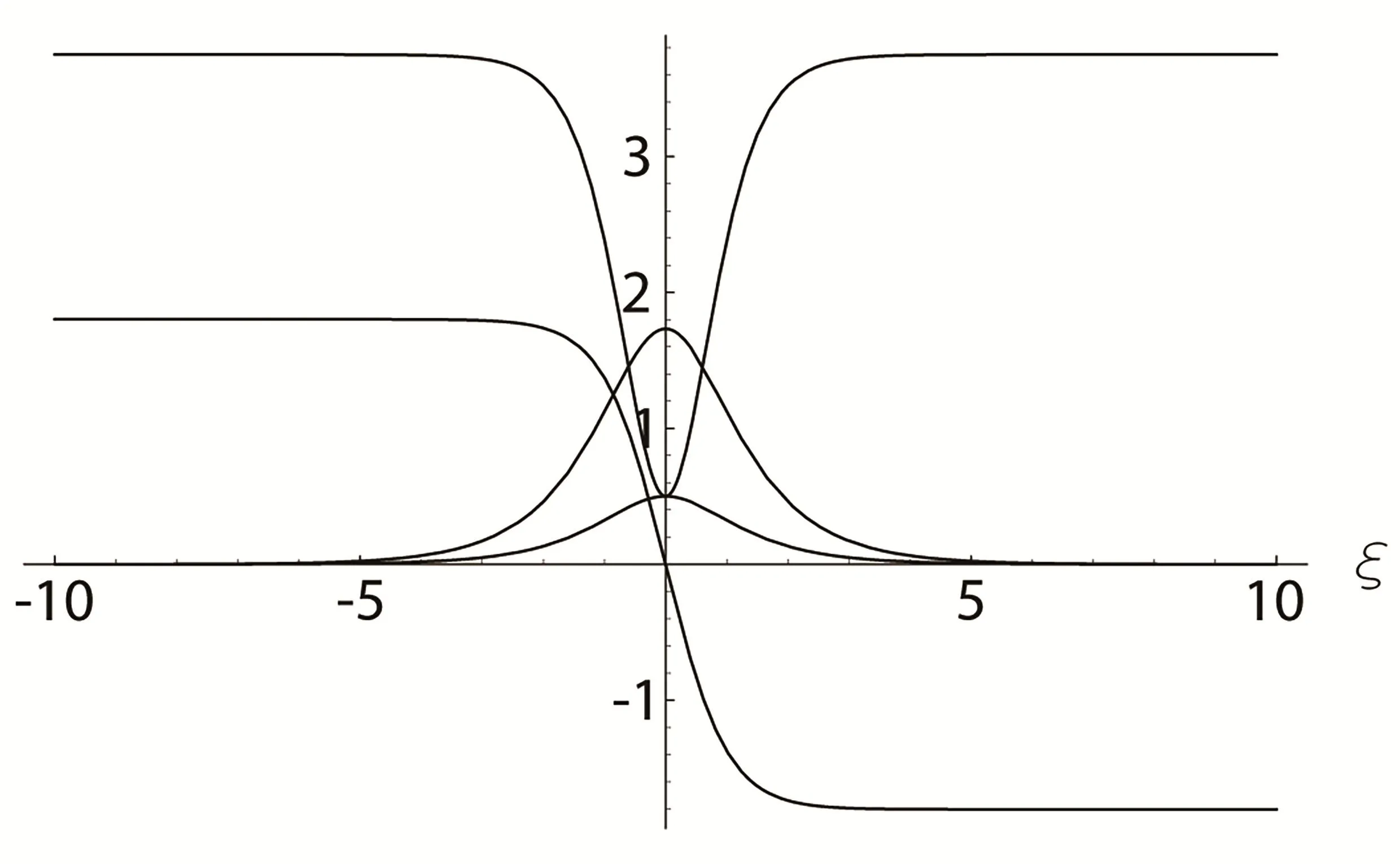
情形1當(dāng)0 圖3 3-耦合方程的Jacobi橢圓函數(shù)解 也就是說,構(gòu)造了方程(2)-(3)新的精確解: 這里條件0 并且需要滿足式子(28).當(dāng)模m→1,上述精確解退化為相應(yīng)的雙曲函數(shù)解,即1-孤子解. 情形2當(dāng)p=N時(shí),類似可得另一個(gè)新的行波解 圖4 3-耦合方程相應(yīng)的1-孤子解 且需要滿足如下式子: 情形3當(dāng)p=0,q=N時(shí),可得如下新的行波解 另外令dn[mξ|m?1]=cn[ξ|m],情形p=q=0 注3.1對(duì)于多分量長(zhǎng)波-短波方程(4)-(5),令 類似于上述計(jì)算過程,可得新的精確解(29)-(30),其系數(shù)為 且需要滿足如下的約束條件 非局部方程有其自身特殊的性質(zhì)和應(yīng)用,已經(jīng)引起專家學(xué)者的極大關(guān)注.例如非局部mKdV方程是一個(gè)可積的無窮維哈密頓系統(tǒng),其作為一個(gè)重要的數(shù)學(xué)模型能很好描述非線性時(shí)空對(duì)稱介質(zhì)中的波傳導(dǎo)現(xiàn)象.典型的非局部方程包括非局部非線性Schr¨odinger方程,非局部離散非線性Schr¨odinger方程[27-36],非局部KdV方程,非局部mKdV方程[37-38]和非局部Davey-Stewartson方程[39-40].非局部離散mKdV方程是一個(gè)新的可積系統(tǒng).在§2中,利用Hirota雙線性方法,構(gòu)造了該方程的1-孤子解,2-孤子解和N-孤子解,并給出了2-孤子解的漸近分析. 對(duì)于多分量Klein-Gordon方程和多分量長(zhǎng)波-短波方程,直接構(gòu)造了新的Jacobi橢圓函數(shù)解.當(dāng)模m→1時(shí),這些解退化為相應(yīng)的雙曲函數(shù)解.最后,這些方程的其它的數(shù)學(xué)物理性質(zhì)如Painlev′e性質(zhì),Lie對(duì)稱有待進(jìn)一步研究.
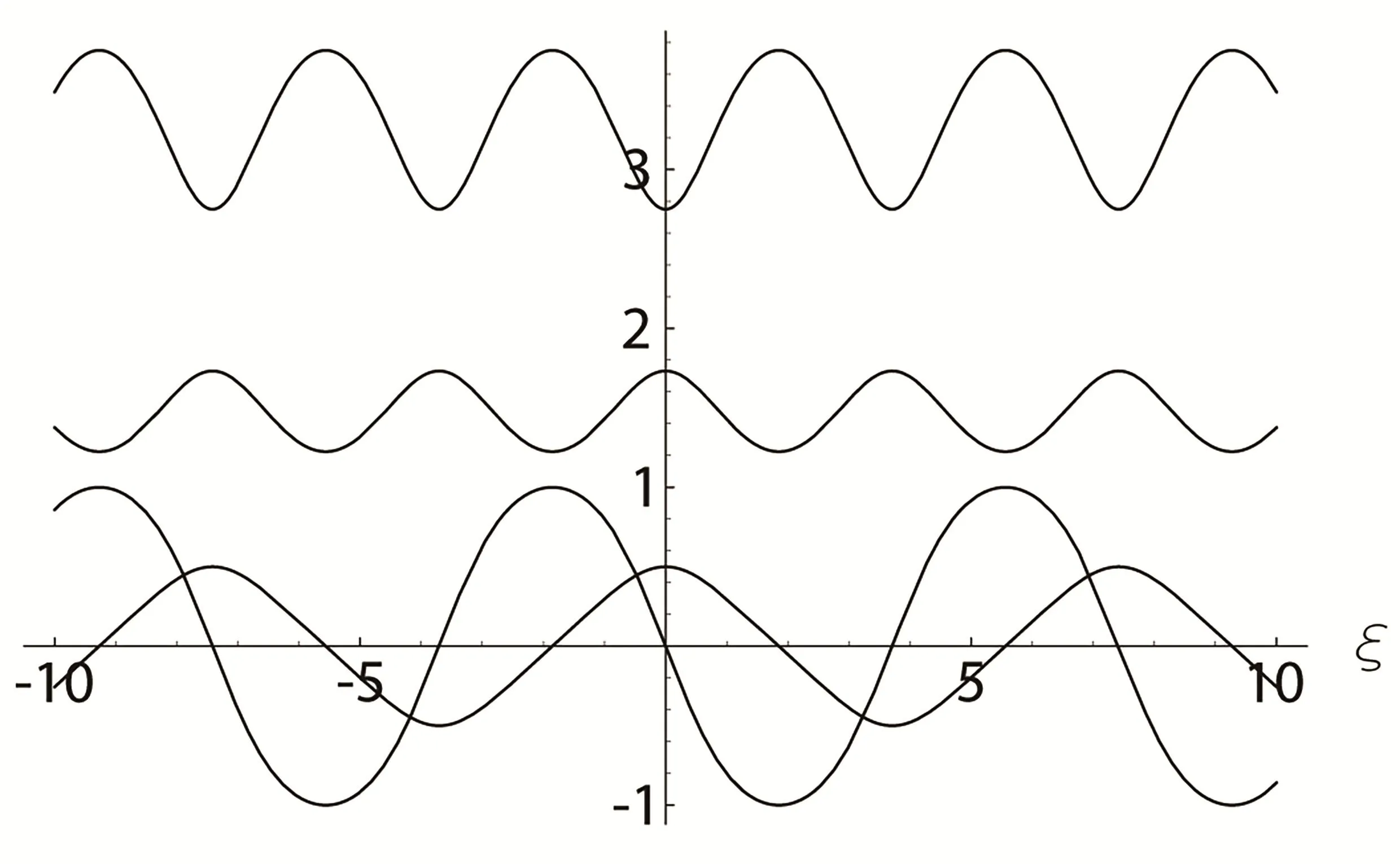
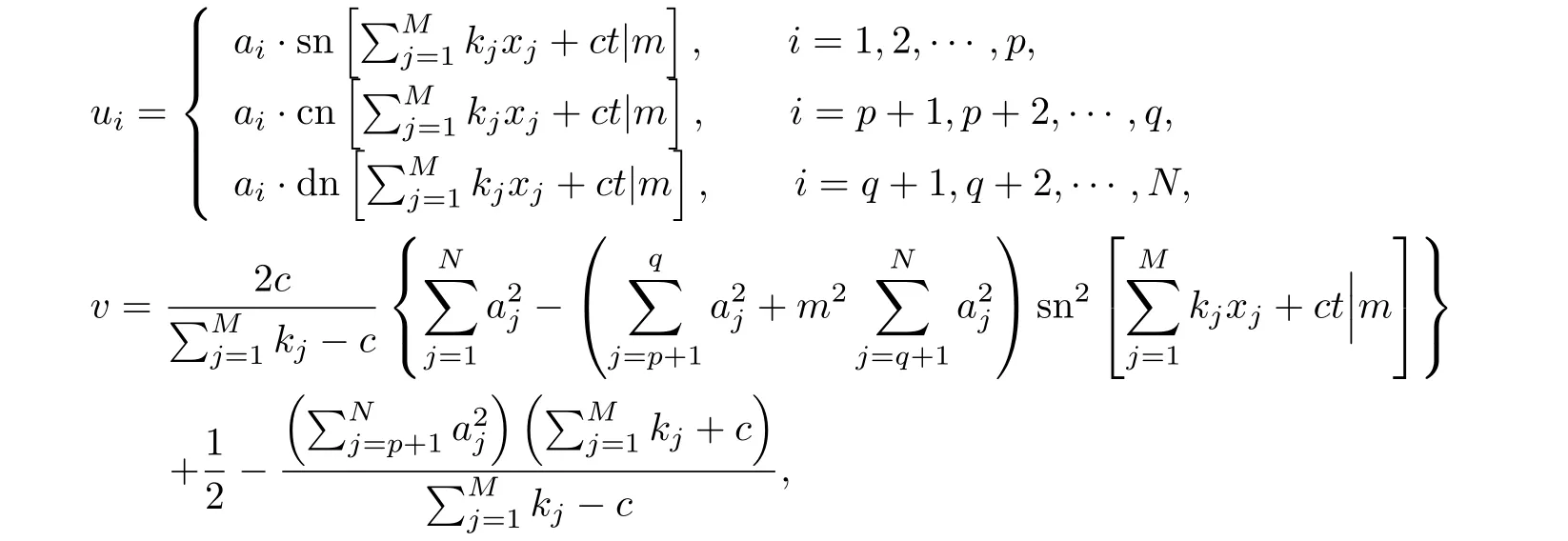
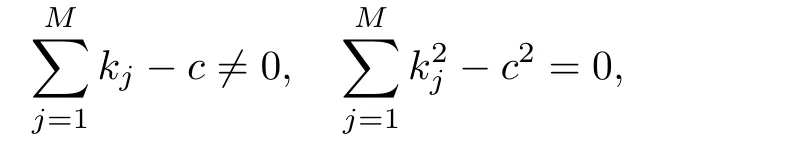
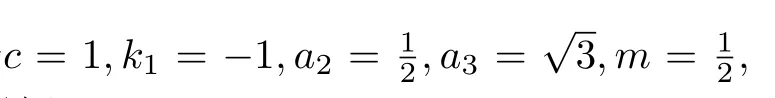
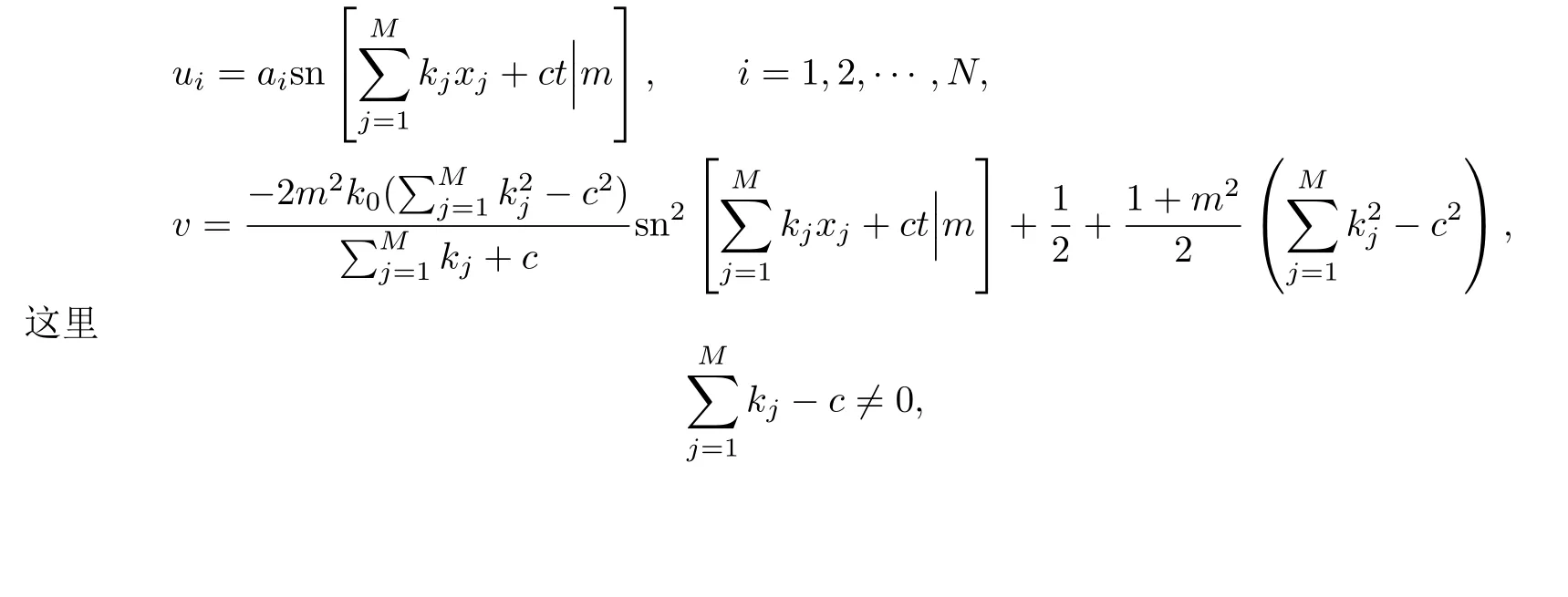
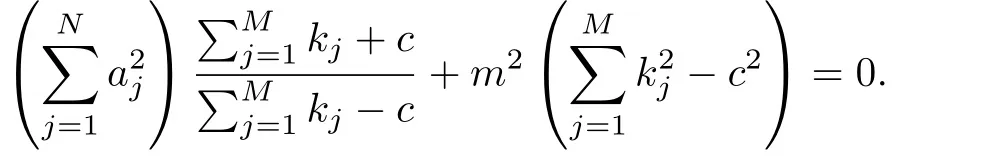
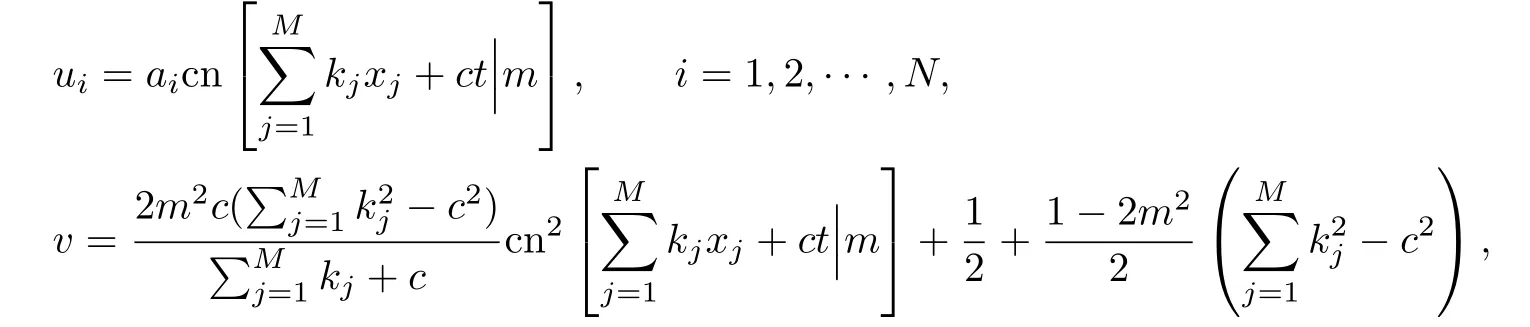
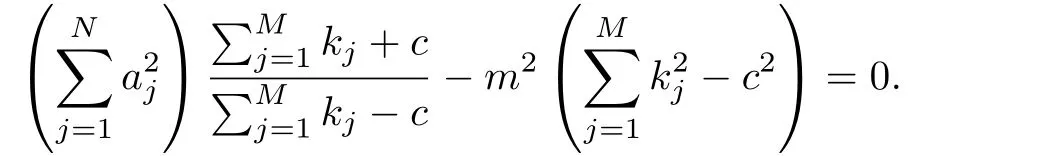
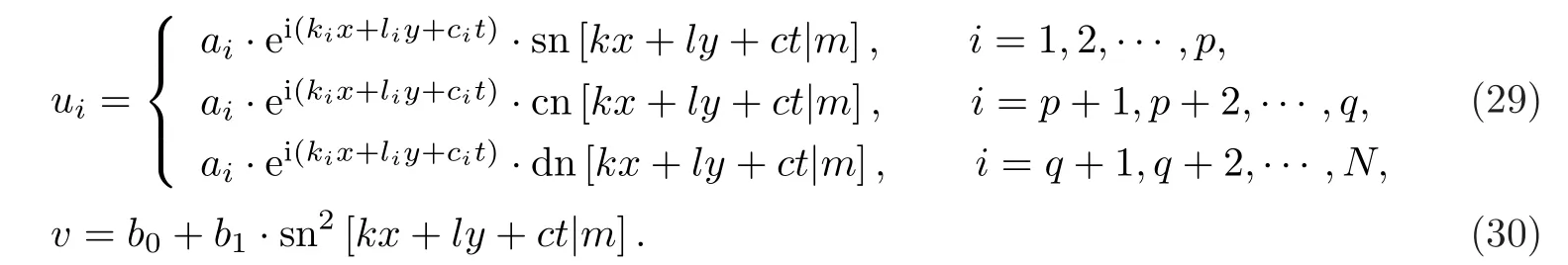
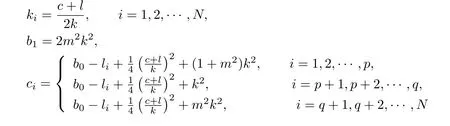
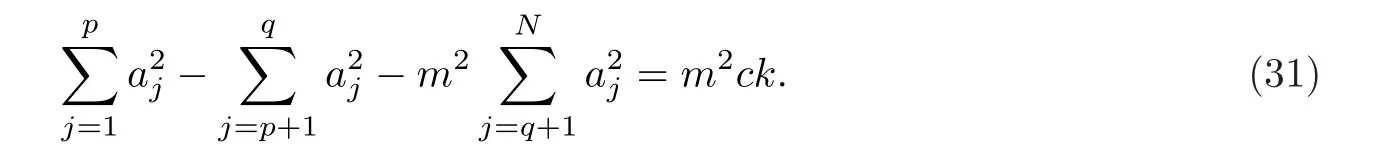
§4 結(jié)論

