基于高階正則與非光滑數(shù)據(jù)擬合項(xiàng)的圖像邊緣檢測(cè)模型①
李 春,陳靜思,王鵬彥,李 健,羅 澤
1(中國(guó)科學(xué)院 計(jì)算機(jī)網(wǎng)絡(luò)信息中心,北京 100190)
2(中國(guó)科學(xué)院大學(xué),北京 100049)
3(云南財(cái)經(jīng)大學(xué) 云南省經(jīng)濟(jì)社會(huì)大數(shù)據(jù)研究院,昆明 650221)
4(四川臥龍國(guó)家級(jí)自然保護(hù)區(qū)管理局,臥龍 623006)
1 圖像分割簡(jiǎn)介
圖像分割和邊緣檢測(cè)是計(jì)算機(jī)視覺(jué),特別是圖像分析中一個(gè)基礎(chǔ)而重要的問(wèn)題(如:目標(biāo)識(shí)別和圖像解析),其目的是把一幅給定圖像根據(jù)其圖像特征(如:邊緣,顏色,紋理,運(yùn)動(dòng),角點(diǎn)特征等)劃分為不同區(qū)域[1].近年來(lái),隨著計(jì)算機(jī)技術(shù)發(fā)展,使得圖像分割成文現(xiàn)代科學(xué)領(lǐng)域的研究熱點(diǎn),圖像分割在醫(yī)學(xué)圖像分析,遙感,監(jiān)測(cè)等領(lǐng)域得到廣泛應(yīng)用[2–11].在諸如物體識(shí)別,分類(lèi)和分割的應(yīng)用中尋找物體邊緣是非常重要的一步.因此,使用和設(shè)計(jì)何種邊緣檢測(cè)算法直接影響這些應(yīng)用性能.如:2019年Yuan等[12]提出了一個(gè)量子圖像邊緣檢測(cè)算法,將邊緣檢測(cè)算法靈活應(yīng)用于量子計(jì)算.圖像邊緣檢測(cè)在雷達(dá)圖像檢測(cè)中也有重要應(yīng)用,Ma等[13]提出通過(guò)稀疏表示進(jìn)行SAR圖像邊緣檢測(cè),作者提出了一種基于去噪算法的新型合成孔徑雷達(dá)(SAR)圖像檢測(cè)算法,該算法通過(guò)稀疏表達(dá)和一種新的形態(tài)學(xué)邊緣檢測(cè)器.首先,作者將Shearlet變換應(yīng)用于SAR圖像以獲得圖像的稀疏表示.然后,將帶方向的形態(tài)學(xué)邊緣檢測(cè)器應(yīng)用于Shearlet的方向子帶系數(shù),其通過(guò)迭代去噪處理來(lái)恢復(fù).2019年Sert等[14]提出了一個(gè)新的基于最大范數(shù)熵的中智學(xué)邊緣檢測(cè)方法.同時(shí),邊緣檢測(cè)算法在醫(yī)學(xué)圖像領(lǐng)域也有重要應(yīng)用,隨著醫(yī)學(xué)領(lǐng)域成像技術(shù)的快速發(fā)展,不同模態(tài)的醫(yī)學(xué)圖像具有不同的成像原理,反映了人體生理信息的不同重點(diǎn)和缺陷.邊緣檢測(cè)是醫(yī)學(xué)超聲圖像處理的關(guān)鍵步驟,檢測(cè)結(jié)果將直接影響醫(yī)生對(duì)疾病的診斷.圖像邊緣檢測(cè)可以看作邊緣點(diǎn)和非邊緣點(diǎn)的分類(lèi)問(wèn)題.基于此,Song等于2019年[15]提出了基于改進(jìn)差分進(jìn)化算法和Prewitt算子的醫(yī)學(xué)圖像邊緣檢測(cè).Churchill等于2019年[16]提供了理論證據(jù)來(lái)解釋邊緣位置在CT影像重建中的潛在重要性.然后開(kāi)發(fā)一種實(shí)用的方案來(lái)利用這一理論.最后,作者通過(guò)實(shí)驗(yàn)證實(shí)了提出的使用邊緣遮蔽正則化可以提高CT重建的準(zhǔn)確性和重建速度.
近年來(lái),基于變分法和偏微分方程(PDES)的圖像分割方法得到了廣泛研究[17–24].早期圖像分割模型代表為活動(dòng)輪廓模型,活動(dòng)輪廓模型根據(jù)圖像邊緣信息和區(qū)域信息對(duì)給定圖像進(jìn)行分割.基于邊緣信息和區(qū)域信息考慮,Kass等于1988年提出基于邊緣信息的能量最小化方法,即,Snake模型[25].其后,受到Snake活動(dòng)輪廓模型啟發(fā),Caselles等提出了綜合活動(dòng)輪廓長(zhǎng)度信息,提出了幾何活動(dòng)輪廓模型[26],與此同時(shí),Mumford和Shah提出了基于區(qū)域信息圖像分割變分框架,即,著名的Munmford-Shah (MS)模型[27].但是,由于MS模型能量泛函的非凸性,導(dǎo)致在當(dāng)時(shí)對(duì)該模型直接求解十分困難.所以,Chan和Vese為了克服MS模型所存在的弊端,并整合了變分法和水平集方法[17],提出了Chan-Vese (CV)模型[28].
由于CV模型應(yīng)用廣泛,所以在過(guò)去幾十年里,該模型一直受到研究學(xué)者青睞.同時(shí),各研究學(xué)者開(kāi)發(fā)各種對(duì)該模型求解的有效方法,例如:為克服初始化輪廓敏感度問(wèn)題,Li等[29]修改CV模型,提出了利用懲罰函數(shù)作為約束且無(wú)需初始化過(guò)程的圖像分割模型.2014年Duan等[30]綜合了變量分離法,對(duì)偶方法,Bregman迭代和增廣的拉格朗日方法提出了更快更有效更的算法.這些算法在高計(jì)算精度和無(wú)需初始化方面取得重要成果.
隨著計(jì)算機(jī)技術(shù)的發(fā)展,深度學(xué)習(xí)在圖像分割中取得重要進(jìn)展,最顯著的進(jìn)展是深度卷積神經(jīng)網(wǎng)絡(luò)(CNNS)不斷被應(yīng)用到場(chǎng)景解析中.典型的網(wǎng)絡(luò)包括:DeepLab (V1-V3)[31,32],Refinenet[33],PSP-Net[34]和DANet[35],然而,這些模型的缺點(diǎn)是計(jì)算代價(jià)相當(dāng)大,需要學(xué)習(xí)的參數(shù)特別多,為了降低這些模型在場(chǎng)景解析中的計(jì)算復(fù)雜度,過(guò)去幾年里,很多學(xué)者在降低計(jì)算復(fù)雜度方面做了大量工作.例如:ENet[36],ESPNet[37]大量減少了需要學(xué)習(xí)的參數(shù).
但是,上述所提的變分優(yōu)化模型中,基本上都是假設(shè)圖像所含噪聲為高斯噪聲,幾乎是用L2范數(shù)對(duì)高斯噪聲加以擬合.然而在現(xiàn)實(shí)生活中,情況相對(duì)較為復(fù)雜,往往圖像在成像時(shí)還有來(lái)自外加噪聲的污染,幸運(yùn)的是,外加噪聲可以用L1范數(shù)得以很好擬合[38,39].利用L1范數(shù)作為數(shù)據(jù)擬合項(xiàng)作為分段常數(shù)圖像分割模型,并利用二階正則函數(shù)(TV2)對(duì)目標(biāo)函數(shù)加以懲罰,使得所提出模型能更好地逼近目標(biāo)函數(shù)的同時(shí)還能能更好地分割低對(duì)比度和含有外加噪聲的圖像.再者,本文通過(guò)變量分離方法把一復(fù)雜非凸問(wèn)題轉(zhuǎn)換為若干個(gè)簡(jiǎn)單凸子問(wèn)題進(jìn)行求解,從而巧妙地處理了不可導(dǎo)項(xiàng)和正則項(xiàng).
2 預(yù)備知識(shí)
在本節(jié)中,因?yàn)锳lternating Direction Method of Multipliers (ADMM)或Split Brgman迭代[40]方法是求解線(xiàn)性約束凸二次規(guī)劃問(wèn)題的有效方法,所以在此對(duì)該方法做如下簡(jiǎn)單介紹.考慮如下線(xiàn)性約束凸優(yōu)化問(wèn)題:
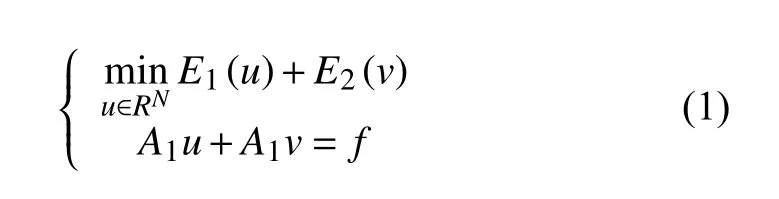
其中,通過(guò)上述目標(biāo)函數(shù),可得如下增廣拉格朗日泛函:
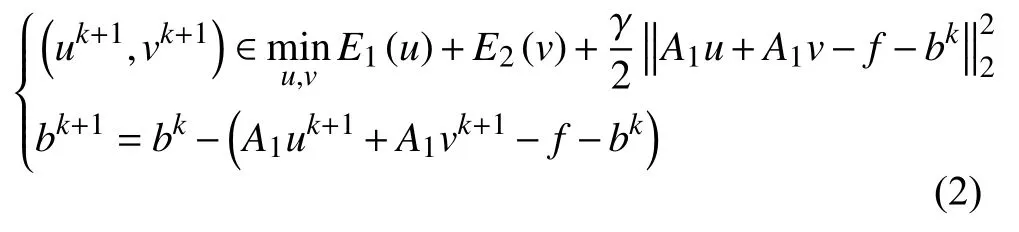
當(dāng)上述系統(tǒng)方程滿(mǎn)足某些收斂條件時(shí),ADMM方法在(2)中固定v更新u,固定u更 新v.因此,ADMM算法可以總結(jié)如算法1.
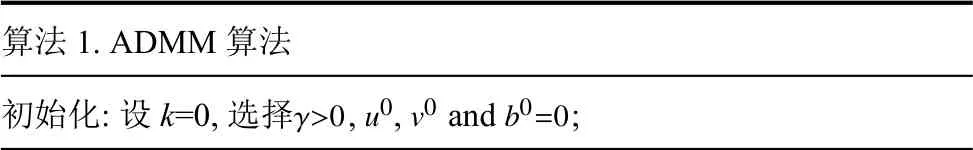
算法1.ADMM算法γ>0u0v0 b0=0初始化:設(shè)k=0,選擇 ,,and ;

for do(1)解問(wèn)題argmin k=1,2,3,···,K u E1(u)+γ 2A1u+A2v?f?bk2 2;(2)求解問(wèn)題argmin u E2(v)+γ 2A1u+A2v?f?bk2 2;(3)拉格朗日乘子更新bk+1=bk?(A1uk+1+A2vk+1?f);end
3 模型提出與數(shù)值求解
在本節(jié)中將介紹所提出的高階正則圖像輪廓檢測(cè)算法,隨后用變量分離法和ADMM算法對(duì)該模型詳細(xì)優(yōu)化過(guò)程和部分收斂性分析加以描述.
設(shè)f:[0,1]2→R?L1(?)為觀測(cè)到信號(hào)(圖像),且滿(mǎn)足如下數(shù)學(xué)表達(dá)式,f=u+n,其中u為未受噪聲污染信號(hào)(圖像),n為外加噪聲(IN).為了重建u,可以考慮如下優(yōu)化問(wèn)題:
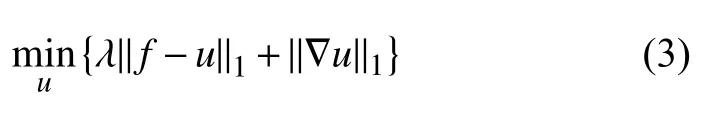
其中,?u為u的 分布導(dǎo)數(shù),∥ ?u∥1為著名的total variation(TV)[41]有界變差空間中的半范數(shù),λ>0為權(quán)參數(shù).若用L2-數(shù)據(jù)擬合項(xiàng) ∥f?u∥2替代∥f?u∥1數(shù)據(jù)擬合項(xiàng),從而可得經(jīng)典的Rudin-Osher-Fatemi (ROF)[41]模型.從而圖像分割模型數(shù)學(xué)表達(dá)式如下:
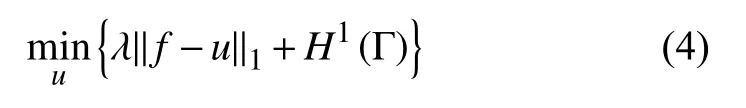
其中,Γ 為u的 不連續(xù)集合,H1為一維的Hausdorff測(cè)度,即,Γ的長(zhǎng)度.
假設(shè)區(qū)域 [0,1]2被劃分為如下的N個(gè)區(qū)域,?1,?2,···,?N且同時(shí)滿(mǎn)足∪i=1,···,N?i=[0,1]2,?i∩?j=?,ij,且對(duì)于所有的i具 有ci∈R.特別地,當(dāng)N=2可以得到除了數(shù)據(jù)擬合項(xiàng)之外,其他都類(lèi)似于CV模型的模型.
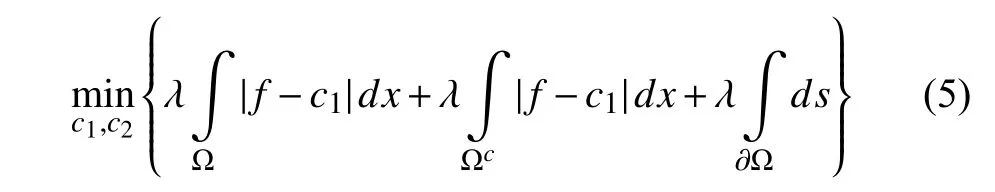
由于 ∥f?u∥1不 可微,所以可以通過(guò)迭代得出c1c2近似解.在圖像恢復(fù)中,盡管基于TV[41]正則已經(jīng)取,得了很好的效果,但是在圖像恢復(fù)過(guò)程中TV正則會(huì)引起階梯效應(yīng).而高階正則不僅有可以去除階梯效應(yīng)的功能,而且高階正則還有光滑區(qū)域,很好地保持物體邊緣的效果,在本模型的實(shí)驗(yàn)過(guò)程中,假設(shè)圖像都是帶有噪聲的,又因?yàn)楦唠A正則比低階正則更具有光滑性和非線(xiàn)性性,所以為了更高的提取邊緣信息,綜合Jung等[38]提出的模型,我們提出如下的高階正則圖像邊緣檢測(cè)模型:
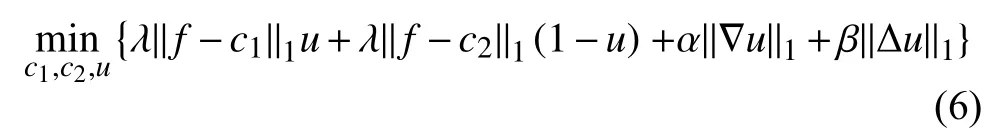
通過(guò)觀察上述目標(biāo)函數(shù)可以發(fā)現(xiàn),為了對(duì)該目標(biāo)泛函進(jìn)行求解,(c1,c2,u),即,兩步驟算法:第1步:先固定u求解c1,c2,第2步:固定c1,c2求解u.同時(shí)并對(duì)離散的散度算子做了如下定義,且散度算子div:(RM×N)2→RM×N具有如下的共軛性質(zhì).?div.u=p.?u,?u∈RN×M,p∈(RM×N)2.
故此,離散散度算子可以作如下定義:對(duì)
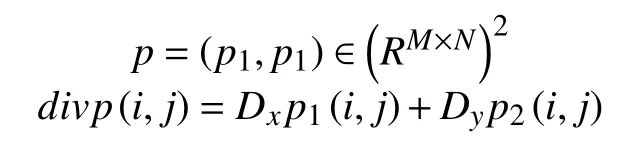
其中,Dx和Dy為如下的向前向后分算子.
以此類(lèi)推,離散二階散度算子定義如下:div2:(RN×M)4→RN×M.且具有如下共軛性質(zhì):div2q.u=q.?u,?u∈RM×N,q∈(RN×M)4.對(duì)于,q=(q11,q12,q21,q22)∈(RN×M)4,我們定義,div2q(i,j)=Dxxq11(i,j)+Dxyq12(i,j)+Dyyq21(i,j)+Dyxq22(i,j).
在實(shí)際應(yīng)用中,學(xué)者經(jīng)常用算子分離法(split Bregman iteration和ADMM)對(duì)(6)進(jìn)行求解.為達(dá)到求解目的,本文先把(6)無(wú)約束優(yōu)化問(wèn)題轉(zhuǎn)化成一個(gè)有約束優(yōu)化問(wèn)題,從而利用Bregman iteration進(jìn)行求解,引入中間變量的好處在于:通過(guò)引入如下輔助變量,不僅把無(wú)約束優(yōu)化問(wèn)題變成一個(gè)有約束優(yōu)化問(wèn)題,引入輔助變量使用變量分離法把一個(gè)復(fù)雜問(wèn)題分解成若干簡(jiǎn)單子問(wèn)題,使得分別對(duì)各子問(wèn)題求解相對(duì)容易.
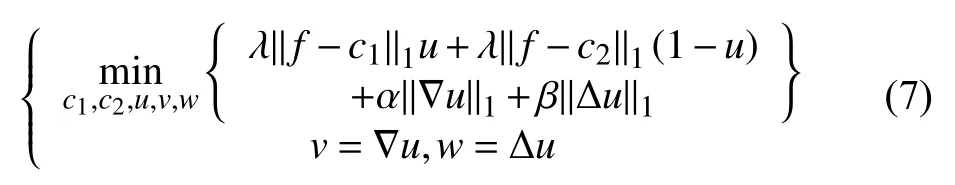
其中,v=(vx,vy),w=(wxx,wyy,wxy,wyx).這里需要進(jìn)行說(shuō)明的是該符號(hào)不是對(duì)v,w分別求導(dǎo),而是表示坐標(biāo).顯而易見(jiàn),無(wú)約束優(yōu)化問(wèn)題(6)和有約束優(yōu)化問(wèn)題(7)等價(jià),從而可以利用ADMM或Split Bregman迭代進(jìn)行求解.其中,問(wèn)題(7)等價(jià)于:

Bregmen迭代算法總結(jié)如算法2.

算法2.Bregman迭代圖像邊緣檢測(cè)算法u1=u0,v1=?u0,w1=?u0 bk1=0,bk2=0初始化:設(shè)k=0,選擇 and ;for do 計(jì)算(8)的最優(yōu)解;bk+1 k=1,2,3,···,K 1 =bk1+vk+1??uk+1 更新:;2 =bk2+wk+1??uk+1 更新:;bk+1 end
直接對(duì)(8)求解時(shí)十分困難,從而可把上式分離成多個(gè)單變量,即,把一個(gè)復(fù)雜問(wèn)題分解成幾個(gè)子問(wèn)題求解.Split Bregman iteration第一次被Goldstain和OSher[40]提出,它在很多寬松條件下等價(jià)于ADMM算法.該方法被廣泛地應(yīng)用到圖像噪聲去除,圖像去模糊,圖像修補(bǔ)等相關(guān)領(lǐng)域.
3.1 u-子問(wèn)題
對(duì)u-子問(wèn)題進(jìn)行求解時(shí)首先固定r=|f?c1|+|f?c2|.得到如下目標(biāo)泛函:
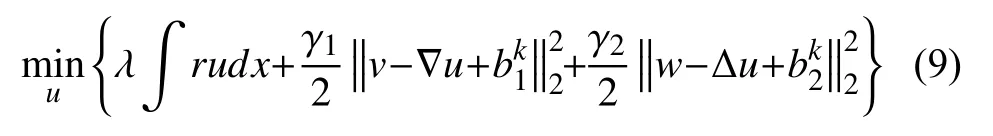
此優(yōu)化問(wèn)題可以通過(guò)其優(yōu)化條件加以求解,在連續(xù)情況下,其解為四階線(xiàn)性PDE,離散情況,其優(yōu)化條件如下:
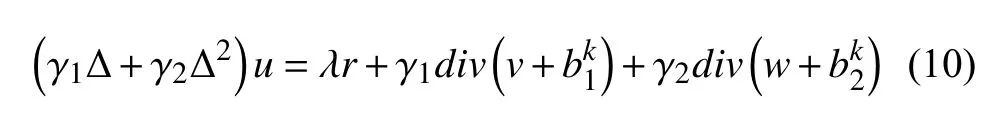
通過(guò)FFT (快速傅里葉變換)可以得到(10)如下近似解.其中,F 代表傅里葉變換,F?1代表傅里葉的逆變換.
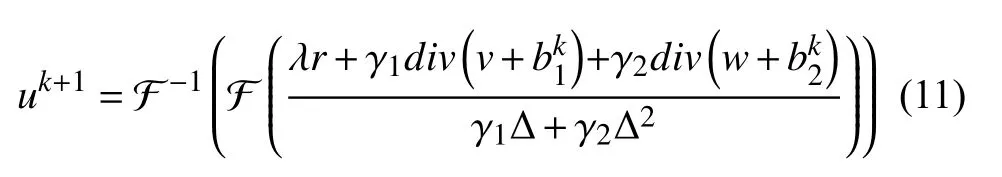
3.2 v-子問(wèn)題
v-子問(wèn)題等價(jià)于求解如下優(yōu)化問(wèn)題:
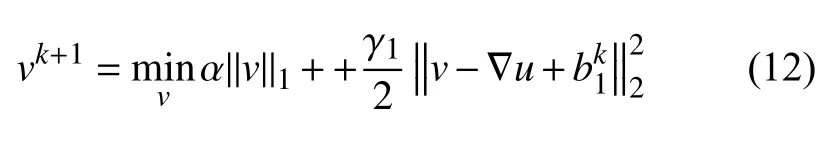
上述優(yōu)化問(wèn)題的解可以使用收縮算子[42]表達(dá),其解析表達(dá)如下:
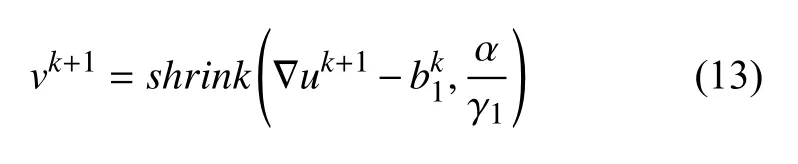
其中,收縮算子shrink(x)[42]定義如下:
對(duì)于任意點(diǎn)α ∈[0,1]2,為了方便起見(jiàn),令
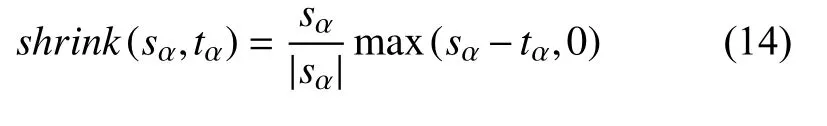
3.3 w-子問(wèn)題
w-子問(wèn)題滿(mǎn)足如下優(yōu)化條件:
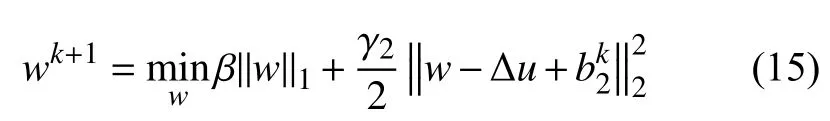
類(lèi)似于v-子問(wèn)題,上述優(yōu)化問(wèn)題解為具有收縮性質(zhì)的軟閾算子.
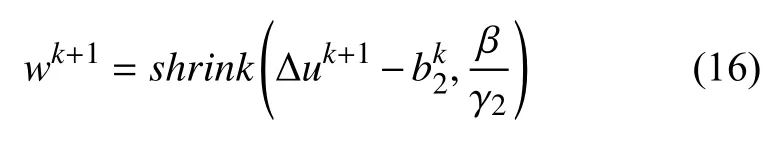
為了說(shuō)明收縮算子的表達(dá)效果和設(shè)置依據(jù)我們考慮如下的一維最小值問(wèn)題加以說(shuō)明:
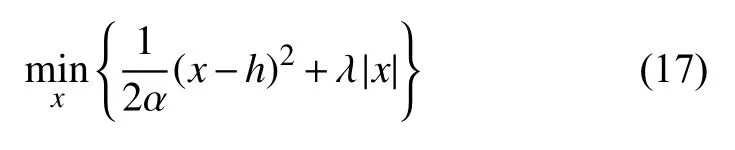
其中,x,h都為標(biāo)量.令可得:

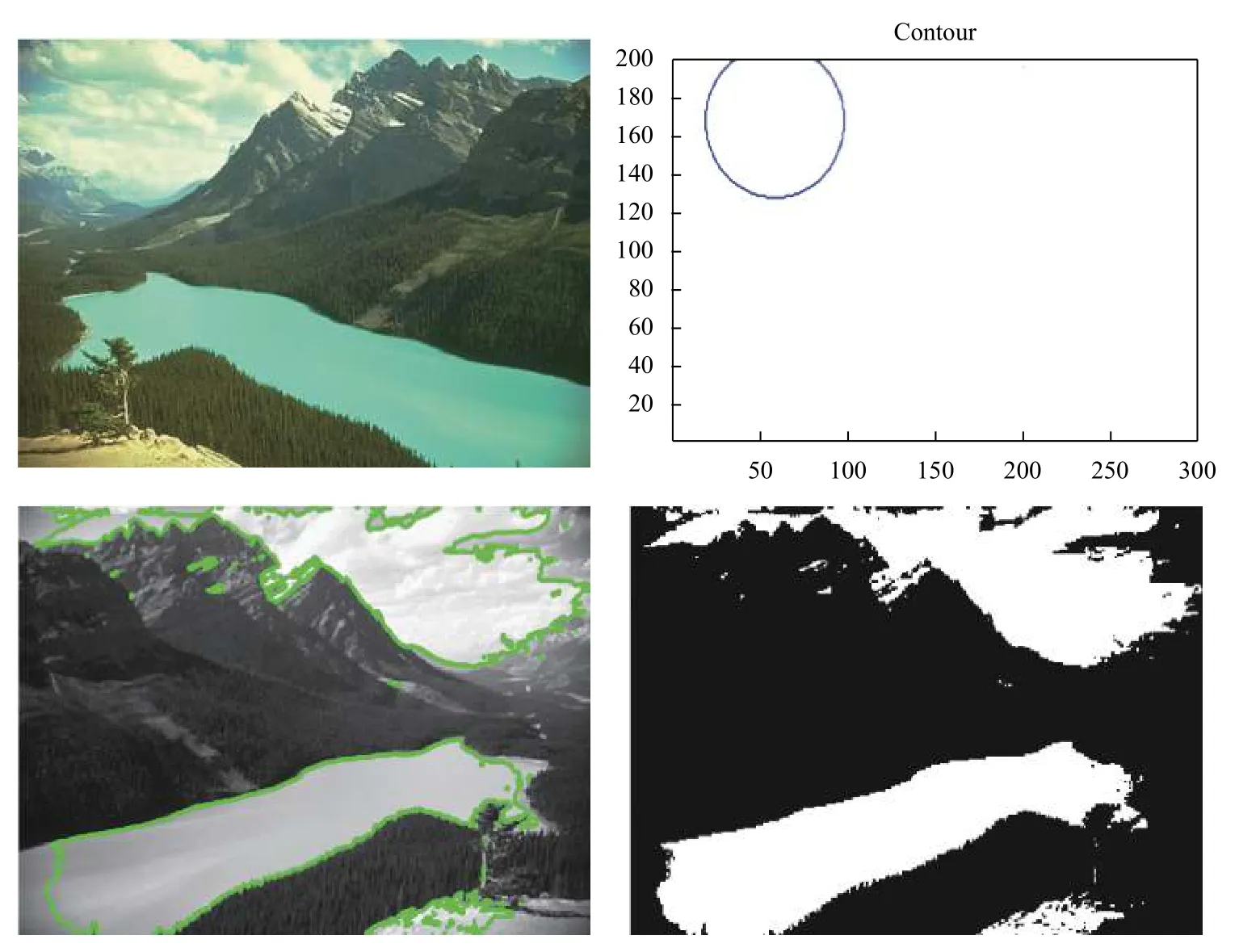
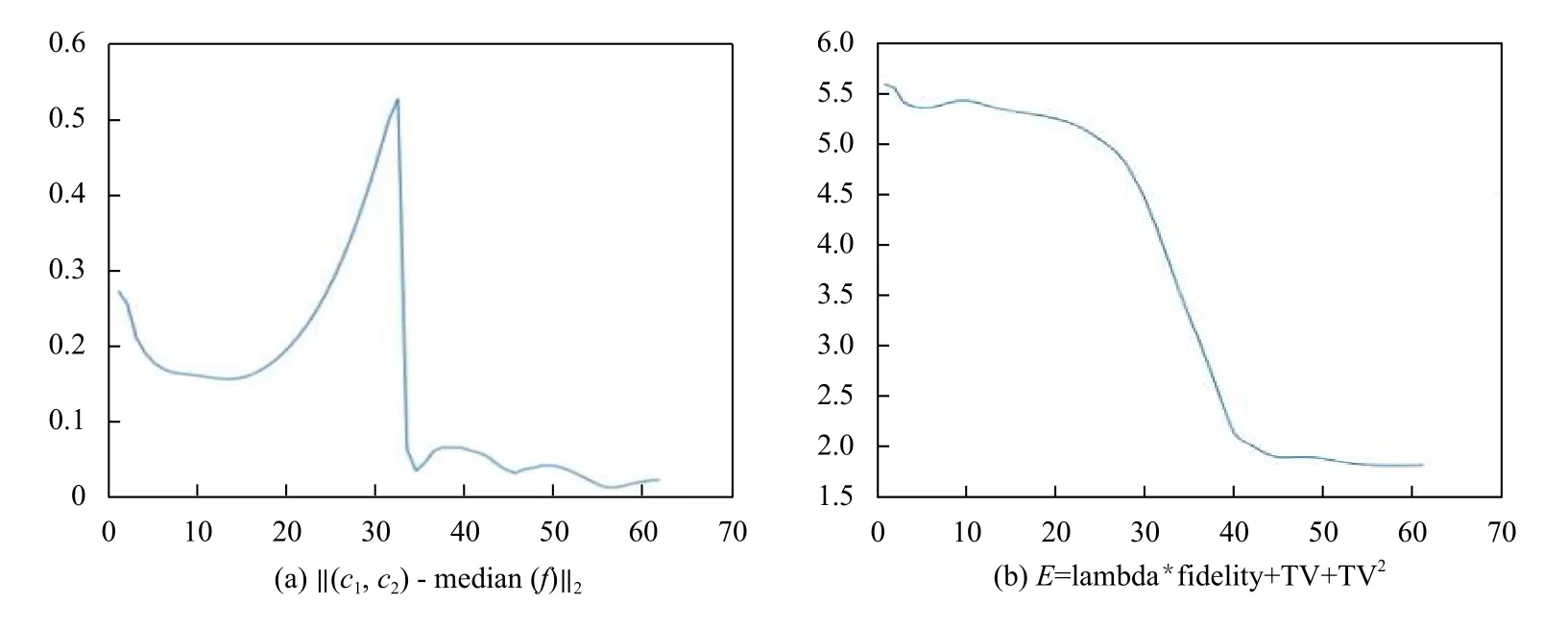
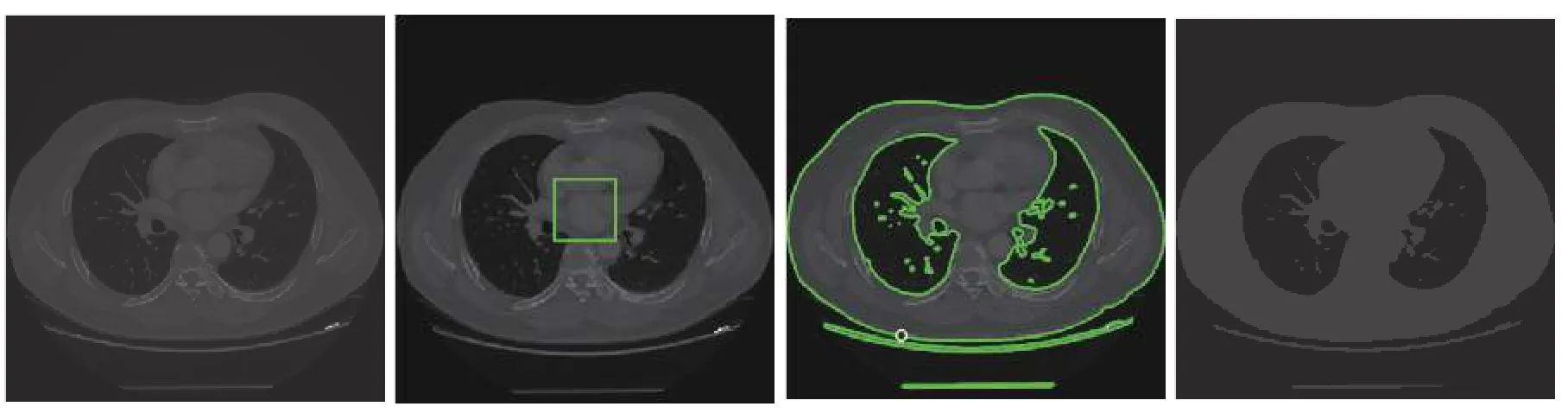
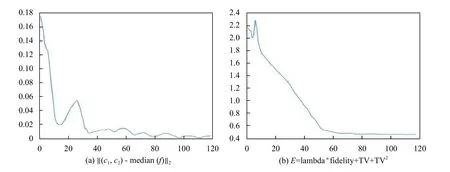
當(dāng)h≥λα?xí)r ,Q(x)的 最小值為h?λα≥0;當(dāng)h≤?λα?xí)r,Q(x)的最小值為h+λα≤0 ;當(dāng)? λα 收縮算子對(duì)稀疏解是有利的,最終大量的h值會(huì)趨近于區(qū)間[ ?λα,λα]的 某個(gè)值從而使得x變 得稀疏.當(dāng)λ 值越大,區(qū)間[ ?λα,λα]就 越大,從而使得x的解就越稀疏. 對(duì)于本模型來(lái)說(shuō)若圖像的大小為N×N,以式(13)為例,其線(xiàn)性時(shí)間復(fù)雜度為O (N2),所以,v,w-子問(wèn)題可以被快速求解,綜上所述,對(duì)于v,w-子問(wèn)題我們?cè)O(shè)置了如式(14)的收縮算子是合理的. 現(xiàn)考慮如下最小值問(wèn)題,從而得到c1,c2的近似解.先固定u,得到如下最小值問(wèn)題: 其中,當(dāng)i=1時(shí) ,h=u,當(dāng)i=2 時(shí) ,h=1?u. 首先我們定義區(qū)域 [0,1]2上的特征函數(shù),χ=從而常數(shù)值ci可以用如下的表達(dá)式來(lái)代替χci,從而可以重寫(xiě)最小值(20): 其中, 為使用變量分離法,故此引入如下輔助變量, 式(23)可以通過(guò)ADMM或Split Bregman迭代進(jìn)行求解. 從而,cki+1和eki+1的近似解解析表達(dá)式為: 故此ADMM圖像邊緣檢測(cè)算法總結(jié)如算法3. 算法3.ADMM圖像邊緣檢測(cè)算法λη1η2α β>0γ1,γ2>0,bk1=v0=0,bk2=w0=0,e0i=d0i=0 u0=1 ??[0,1]2初始化:設(shè)k=0,選擇,,,,,在某些區(qū)域 ,0其他;k=1,2,3,···,K for do hk=uk i=1hk=(1?uk),i=2 if ,,ck+1 i ck+1 i i=1,2 計(jì)算 :用式(27)計(jì)算 ,;ek+1 i ek+1 i i=1,2 計(jì)算 :用式(28)計(jì)算 ,;dk+1 i dk+1 i i=1,2f?ck+1 計(jì)算 :用 ;更新 :用式(26)計(jì)算 ,;rk+1 rk+1=f?ck+1 1 2 vk+1 vk+1 計(jì)算 :用式(13)計(jì)算 ;wk+1 wk+1 計(jì)算 :用式(16)計(jì)算 ;uk+1 uk+1 計(jì)算 :用式(11)計(jì)算 ;1 bk+11 =bk1+vk+1??uk+1 更新 :;bk+1 2 bk+12 =bk2+wk+1??uk+1 更新 :;bk+1 end 本節(jié)中,受到文獻(xiàn)[38]啟發(fā),本文將給出本算法的部分收斂性分析,最小值問(wèn)題(6)可以通過(guò)引入變量分離辦法重寫(xiě)成有約束條件: 其對(duì)應(yīng)的拉格朗日泛函如下: 其中,μ1,μ2,μ3為對(duì)偶變量. 設(shè)X?=(c?1,c?2,u?,e?1,e?2,v?,w?,μ?1,μ?2,μ?3,μ?4)為 問(wèn) 題(29)的KKT點(diǎn),則點(diǎn)X?滿(mǎn)足如下的KKT條件: 其中,x⊙y為coordi nate-wise乘法. 定理.設(shè)Xk=(ck1,ck2,uk,ek1,ek2,vk,wk,d1k,d2k,bk1,bk2)為算法3中的迭代,并且,設(shè): 假設(shè), 證明:首先,對(duì)于u-子問(wèn)題等價(jià)于求解最小化問(wèn)題(9),從而得出如下優(yōu)化條件: 其次,從優(yōu)化條件和ADMM算法對(duì)各變量的表達(dá)式可得: 為了說(shuō)明本文提出算法優(yōu)越性,本文將給出該模型在灰度圖像,真實(shí)圖像,含噪聲圖像,CT圖像的分割實(shí)驗(yàn)結(jié)果,在討論結(jié)果之前,本文先作以下說(shuō)明,該算法的迭代終止條件應(yīng)滿(mǎn)足如下的相對(duì)容忍度,即滿(mǎn)足下列條件: 此后,用該模型和Chan-Vese (CV)做比較.該算法與CV模型不同之處在于計(jì)算常數(shù)值ci,i=1,2,對(duì)于CV模型而言,ci,i=1,2在每次迭代過(guò)程中都有具體迭代表達(dá)式.該模型另外一個(gè)優(yōu)點(diǎn)是很少依賴(lài)于初始化位置和微調(diào)參數(shù),在本算法中,η1,η2,α ,β >0 ,γ1,γ2>0,所有參數(shù)都相對(duì)很固定.因?yàn)樵撃P褪且粋€(gè)局部極小值問(wèn)題,不同初始輪廓可能會(huì)收斂到不到能量局部極小值.我們之所以選擇和CV模型作比較,主要原因在于想體現(xiàn)高階正則模型與低階正則模型對(duì)圖像邊緣檢測(cè)不同效果影響. 圖1為CV模型和新模型對(duì)飛機(jī)圖像的分割效果圖,其中,第一,二行分別代表CV模型和高階正則模型對(duì)飛機(jī)圖像的分割效果圖;第一列代表原始圖像,第二列分別代表CV模型和高階正則模型對(duì)飛機(jī)圖像的初始化輪廓;第三列分別代表CV模型對(duì)飛機(jī)圖像迭代800次時(shí)的邊緣檢測(cè)情況和高階正則模型對(duì)飛機(jī)圖像迭代80次時(shí)的邊緣檢測(cè)情況;第四列分別代表CV模型對(duì)飛機(jī)圖像迭代800次時(shí)的實(shí)際分割效果圖和高階正則模型對(duì)飛機(jī)圖像迭代80次時(shí)的實(shí)際分割效果圖. 圖1 CV模型和高階正則模型對(duì)飛機(jī)圖像的檢測(cè)效果圖 圖2表示CV模型對(duì)自然風(fēng)景圖像的分割效果圖,圖3表示高階正則模型對(duì)自然風(fēng)景圖像的分割效果圖.其中圖2的4幅圖分別為:第一幅代表原始圖像,第二幅代表CV模型對(duì)自然風(fēng)景圖像的初始化輪廓,第三幅代表CV模型對(duì)自然風(fēng)景這幅圖像迭代800次時(shí)的邊緣檢測(cè)圖,第四幅代表CV模型對(duì)自然風(fēng)景這幅圖迭代800次時(shí)的實(shí)際分割效果圖.圖3的4幅圖分別代表的意義為:第一幅為原始圖像,第二幅為高階正則模型對(duì)自然風(fēng)景圖像的初始化輪廓圖,第三幅圖像表示高階正則模型對(duì)自然風(fēng)景圖迭代200次時(shí)的邊緣檢測(cè)圖,第三幅圖像表示高階正則模型對(duì)自然風(fēng)景圖迭代200次時(shí)的實(shí)際分割效果圖. 圖2 CV模型對(duì)自然風(fēng)景圖像的分割效果圖 從圖4可以看出,CV模型對(duì)自然風(fēng)景這一幅圖像迭代30次后基本收斂,而高階正則模型需要迭代到40次左右才收斂,但是值得注意的是,從兩個(gè)模型對(duì)同一幅圖像Loss函數(shù)曲線(xiàn)圖可知,CV模型基本收斂后Loss函數(shù)曲線(xiàn)圖還有小幅度跳躍情況,然而,高階正則模型收斂后Loss函數(shù)曲線(xiàn)圖相對(duì)更平滑,說(shuō)明其分割效果也很好,更能精確地逼近物體邊界. 下面我們給出一個(gè)例子說(shuō)明該高階正則模型在醫(yī)學(xué)圖像領(lǐng)域的應(yīng)用,圖像分割在醫(yī)學(xué)圖像領(lǐng)域的應(yīng)用就是通過(guò)發(fā)展大量的自動(dòng)或者半自動(dòng)圖像分割方法,精準(zhǔn)分割醫(yī)學(xué)圖像,從而替代醫(yī)生的大量手工標(biāo)注,從而使得醫(yī)生從大量繁重的體力勞動(dòng)中解放出來(lái). 我們用本模型在病人肺部CT圖上做分割實(shí)驗(yàn),如圖5所示,從其分割效果圖得知,高模型不僅能對(duì)病人肺部做精準(zhǔn)分割,CV模型和高階正則模型Loss函數(shù)曲線(xiàn)收斂圖如圖6,可知,新模型Loss函數(shù)曲線(xiàn)圖相對(duì)CV模型而言相對(duì)較光滑,這更能說(shuō)明該模型比CV模型來(lái)更能精確地逼近物體邊界. 需要說(shuō)明的是,在分割過(guò)程中,CV模型的模型參數(shù)設(shè)置均為原始論文的參數(shù),考慮到CV模型的數(shù)據(jù)項(xiàng)數(shù)擬合高斯噪聲,而本文所設(shè)計(jì)的模型數(shù)據(jù)保真項(xiàng)模擬的是外加噪聲,所以,在實(shí)驗(yàn)過(guò)程中,對(duì)于CV模型而言,并沒(méi)有人工地加入任何噪聲.但是,對(duì)于高階正則模型而言,由于本文假設(shè)其成像過(guò)程中可能含有外加噪聲(如:椒鹽噪聲),所以在實(shí)驗(yàn)過(guò)程中我們用Matlab中的加噪聲函數(shù)imnoise(Im0,'salt & pepper' 0.6);每幅原始圖像都人為的加了參數(shù)為0.6的椒鹽噪聲.新模型對(duì)所有圖像分割的迭代總次數(shù)均設(shè)置為200,CV迭代總次數(shù)均設(shè)為800,迭代停止條件為stoppling_tol=–10,λ =20,α =β=1,η1=η2=5 0,γ1=γ1=50. 圖3 高階正則模型對(duì)自然風(fēng)景圖像的分割效果圖 圖4 CV模型和高階正則模型對(duì)自然風(fēng)景圖像分割的Loss函數(shù)曲線(xiàn)收斂圖 圖5 高階正則模型對(duì)病人肺部CT圖像的分割效果圖 圖6 CV模型和高階正則模型對(duì)病人肺部CT圖像分割的Loss函數(shù)曲線(xiàn)收斂圖 本文提出一個(gè)修改的Chan-Vese模型,并引入高階正則函數(shù)對(duì)目標(biāo)函數(shù)進(jìn)行懲罰,然后對(duì)新模型用ADMM或者Split Bregmen迭代算法進(jìn)行數(shù)值求解.再者,本文還分析了該模型的數(shù)學(xué)性質(zhì),并給出該模型的部分收斂性分析,實(shí)驗(yàn)結(jié)果表明,通過(guò)引入高階正則函數(shù)后,該模型不僅能分割對(duì)比對(duì)低的物體,而且還可以探測(cè)帶噪聲的物體.大量實(shí)驗(yàn)表明,該算法在各領(lǐng)域具有廣泛應(yīng)用價(jià)值,在未來(lái)的工作中,我們會(huì)綜合一些深度學(xué)習(xí)的模塊,去探測(cè)物體的landmarks點(diǎn),從而使得算法更自動(dòng),更魯棒.
3.4 c 1,c2-子問(wèn)題
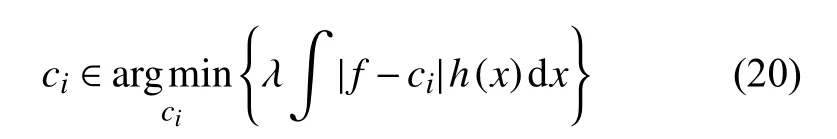
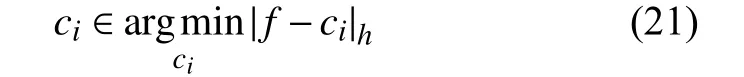
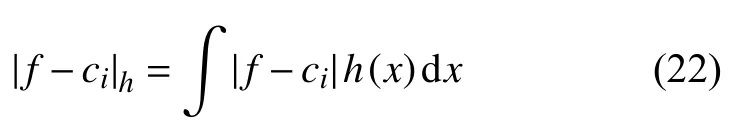

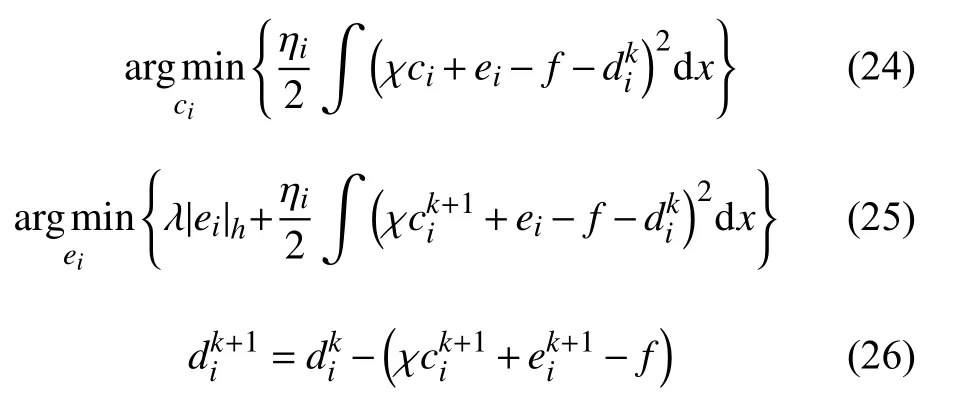
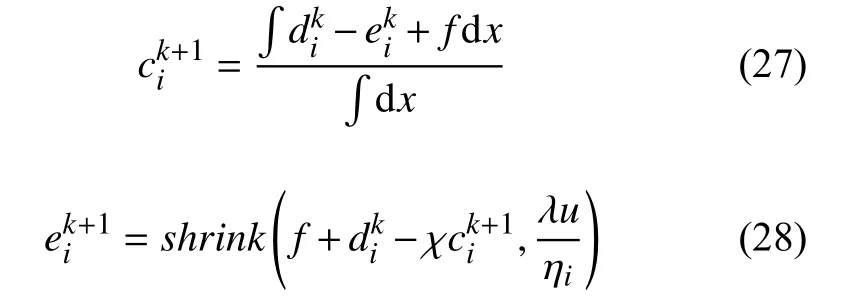

4 算法部分收斂性分析
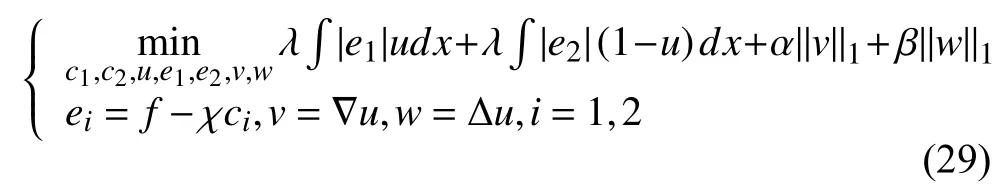
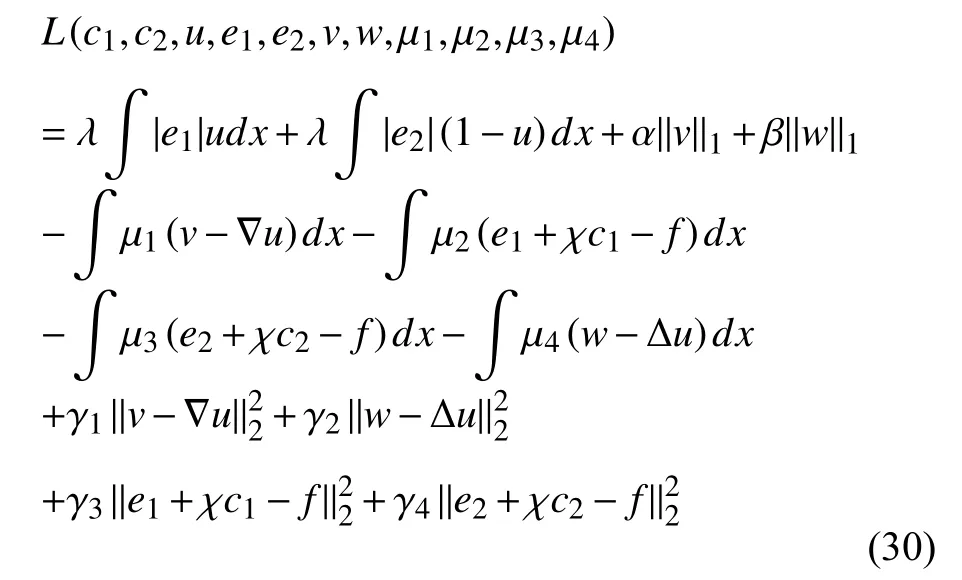
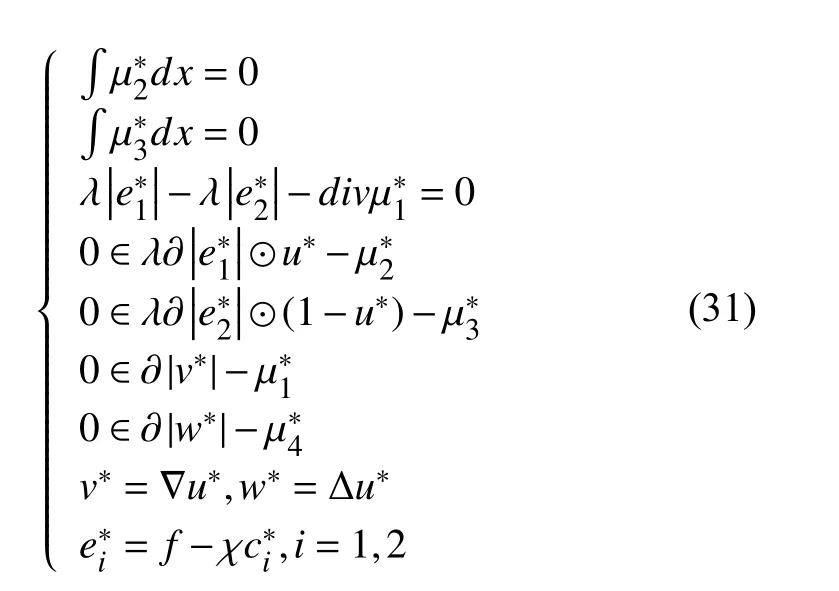
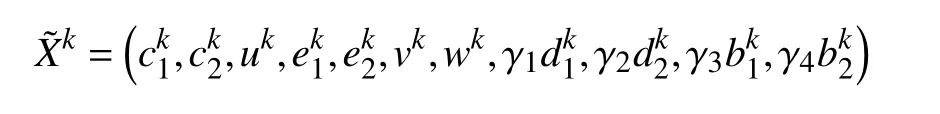
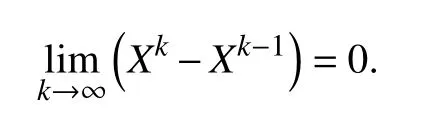
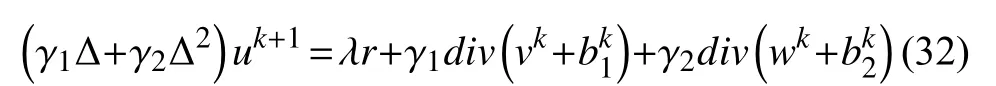


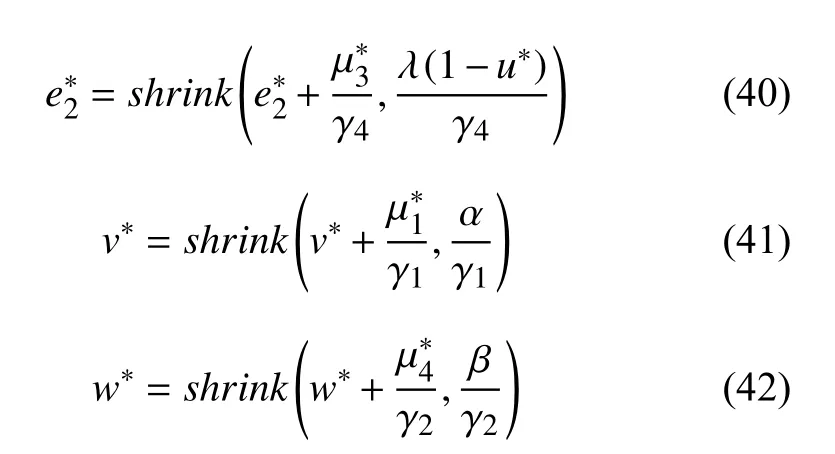
5 實(shí)驗(yàn)結(jié)果


6 總結(jié)與展望

