黎健玲,安婷,曾友芳,鄭海艷

( 廣西大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,廣西 南寧530004)

1.引言

本文考慮如下二次半定規(guī)劃(簡記為QSDP)

其中函數(shù)φ:Sn→Sn為自伴隨線性算子,Sn表示n階實對稱矩陣空間.Ai(i=1,···,m),C和X都是n× n階實對稱矩陣,b∈Rm.表示矩陣的內(nèi)積,即?A∈Rp×q,B∈Rp×q,〈A,B〉=tr(ATB).X ?0 和X ?0 分別表示矩陣X是對稱半正定矩陣和對稱正定矩陣.

凸二次半定規(guī)劃是半定規(guī)劃[1?4]的推廣,其在證券,金融,最優(yōu)控制等領(lǐng)域中有著廣泛的應(yīng)用,因此對凸二次半定規(guī)劃的研究受到學(xué)者們的關(guān)注,并已取得一批研究成果(見文[5–10]).文[5]提出了一個預(yù)估校正算法,該算法至多經(jīng)次迭代可得到一個?最優(yōu)解.文[8]提出了一個非精確原始對偶路徑跟蹤算法.文[9]提出了一個基于參數(shù)核函數(shù)的原始-對偶內(nèi)點算法.

受線性半定規(guī)劃的HKM方向啟發(fā),本文提出一個基于HKM方向的新原始-對偶路徑跟蹤算法.在每次迭代中,算法通過求解一個線性方程組產(chǎn)生HKM搜索方向.在一定條件下證明了算法產(chǎn)生的迭代點列落在中心路徑的鄰域內(nèi),且算法至多經(jīng)O(n|log?|) 次迭代可得到一個?-最優(yōu)解.

在一定的假設(shè)條件下,分析了該算法的迭代復(fù)雜度.

QSDP(1.1)的對偶問題(簡記為QSDD)為

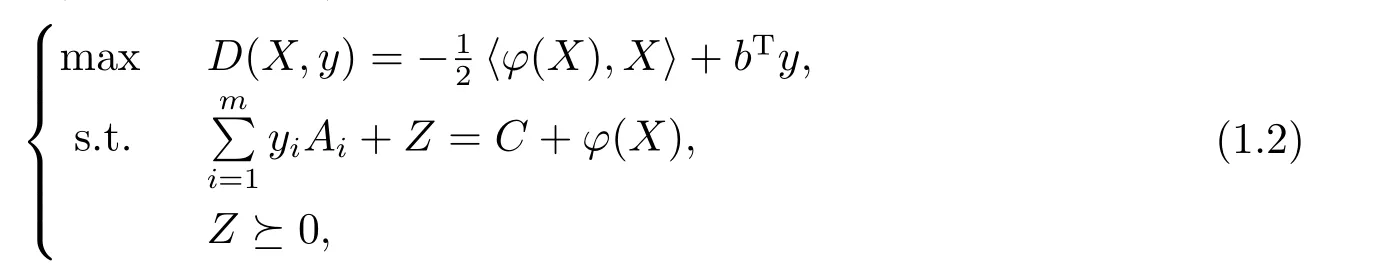
其中y∈Rm,Z∈Sn.

分別記QSDP(1.1)和QSDD(1.2)的可行域為FP和FD,并記F0P和F0D分別為FP和FD的嚴格內(nèi)部,即

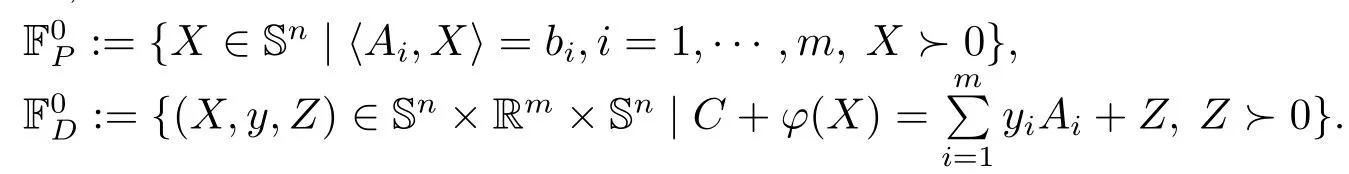
對于任意的可行點X和(X,y,Z),則對偶間隙為

本文需作如下基本假設(shè):

假設(shè)(A1) 線性算子φ(X)是對稱半正定的,即滿足

假設(shè)(A2) Slater約束規(guī)格成立,即存在X ?0,Z ?0,y∈Rm,使得X∈F0P,(X,y,Z)∈F0D;

假設(shè)(A3) 矩陣A1,A2,···,Am線性無關(guān).

2.HKM 方向

稱滿足如下方程組

的點(X,y,Z) 構(gòu)成的集合為中心路徑,其中為中心參數(shù),I為n階單位矩陣.

設(shè)當(dāng)前迭代點為(X,y,Z),且X∈F0P,(X,y,Z)∈F0D.用一步Newton 法求解方程組(2.1),得到下面方程組:

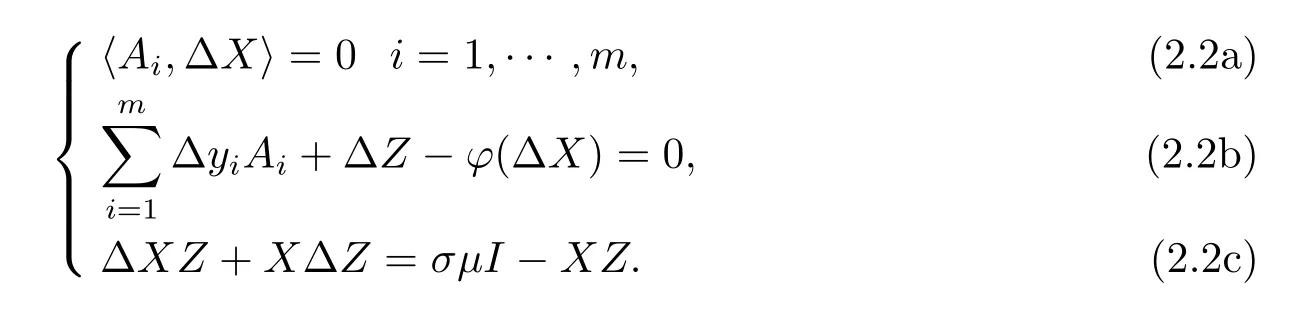
類似線性半定規(guī)劃(見文[2]),HKM 搜索方向(?X,?y,?Z)由下列線性方程組確定:

下面引理給出了線性方程組(2.3)的解(?X,?y,?Z)的性質(zhì).

引理2.1假設(shè)(A1)-(A3)成立,X∈F0P,(X,y,Z)∈F0D,(?X,?y,?Z)是線性方程組(2.3)的解,則下面結(jié)論成立:

證(i)根據(jù)方程(2.3b)和(2.3a)可得

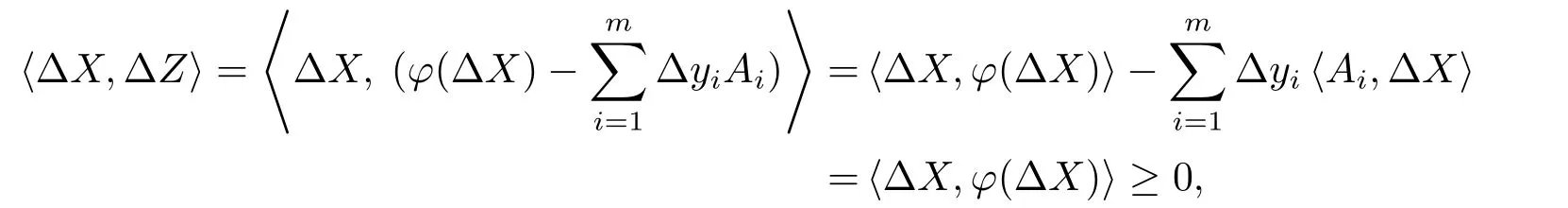
其中最后一個不等式由假設(shè)(A1)得到.于是結(jié)論(i)成立.

(ii)由(2.3c)式得

即結(jié)論(ii)成立.

即結(jié)論(iii)成立.

3.長步原始對偶路徑跟蹤算法

本節(jié)將給出基于HKM方向(?X,?y,?Z)的長步原始對偶路徑跟蹤算法的具體步驟,然后分析算法的性質(zhì).

算法3.1

步1 記(X,y,Z)=

步3 求解方程組(2.3),得到(?X,?y,?Z);

步4 選擇合適的步長α=αk≥0,令(Xk+1,yk+1,Zk+1)=(Xk,yk,Zk)+α(?X,?y,?Z),k:=k+1,轉(zhuǎn)回步1.

本文定義如下中心路徑鄰域:

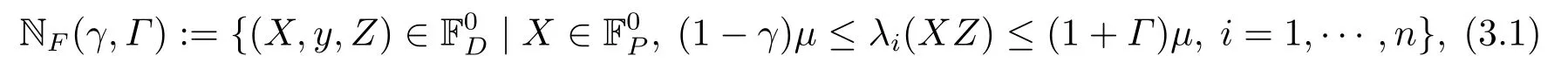
在下面的討論中,為簡便起見,略去指標(biāo)k,例:把(Xk,yk,Zk)簡記為(X,y,Z).

引理3.1假設(shè)(A1)-(A3)成立,X∈F0P,(X,y,Z)∈F0D,(?X,?y,?Z)是線性方程組(2.3)的解,對于任意給定的α>0,令

則

證對于任意給定的α>0,根據(jù)引理2.1(iii)及(3.3),有

因此,有

于是由(3.4)并結(jié)合(3.7),得

將上式進行化簡并結(jié)合(2.3c),得

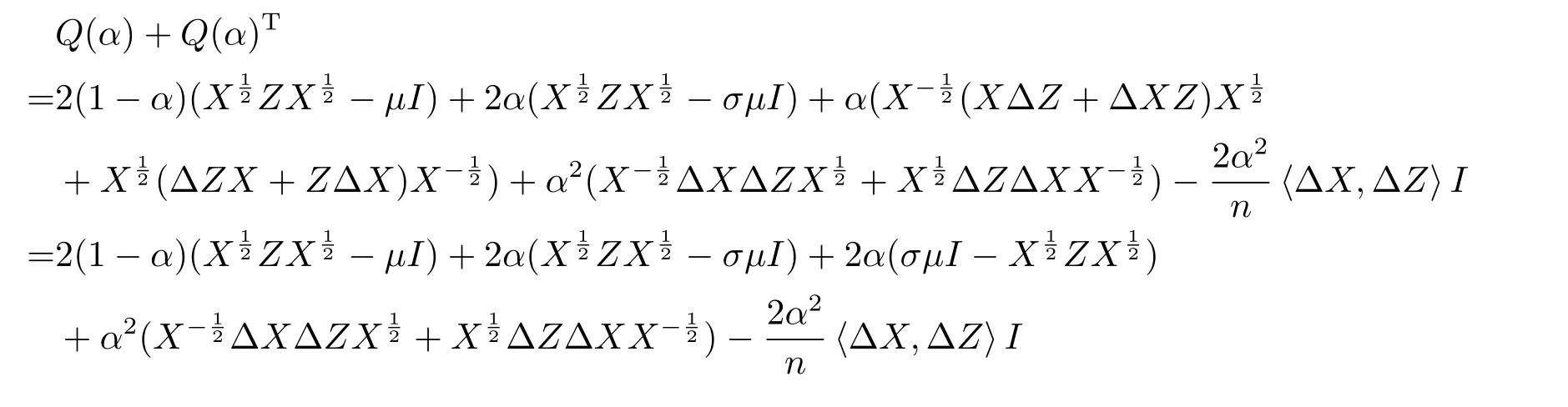
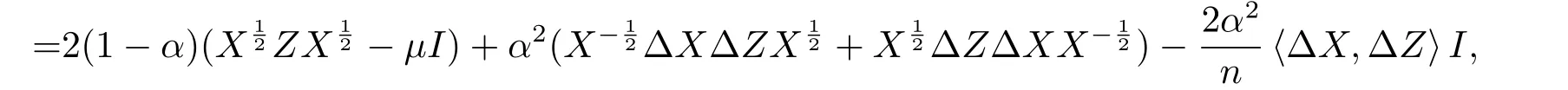
即(3.5)成立.

引理3.2假設(shè)(A1)-(A3)成立,(X,y,Z)∈NF(γ,Γ),(?X,?y,?Z)是線性方程組(2.3)的解,則

其中μ(α)的定義見(3.3),且

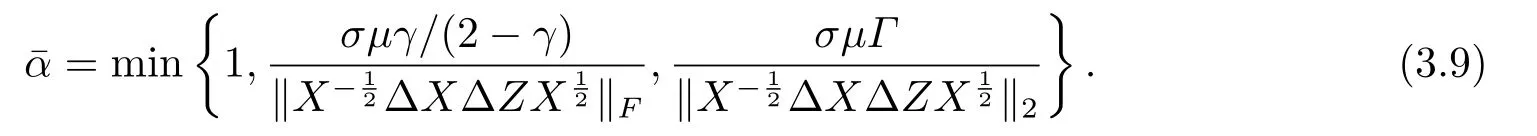
證由(X,y,Z)∈NF(γ,Γ)知

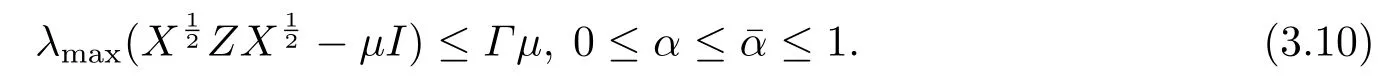
由(3.5)及λmax(·)為凸函數(shù)知

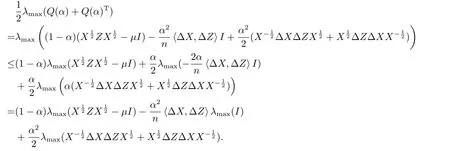
結(jié)合(3.10),(3.6),引理2.1(1)及文[2]中的引理3.1 可得

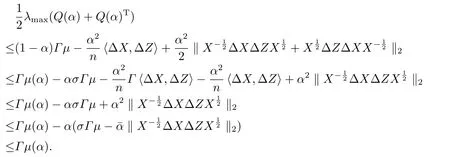
最后一個不等式源自(3.9).由此可知(3.8)式右邊不等式成立.

同理,由(X,y,Z)∈NF(γ,Γ)知

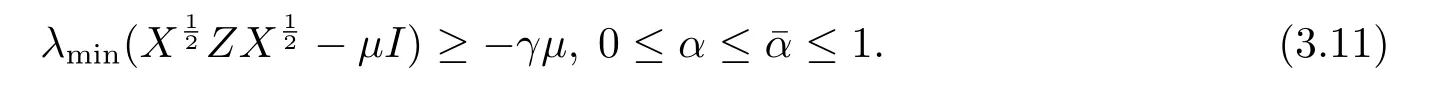
由(3.5)及λmin(·)是凹函數(shù)知

結(jié)合(3.11),(3.6)及文[2]的引理3.1 可得

由‖·‖F(xiàn)的定義得

最后一個不等式源自(3.9).因此,(3.8)左邊不等式成立.

綜上可知本引理成立.

引理3.3假設(shè)(A1)-(A3)成立,(X,y,Z)∈NF(γ,Γ),(?X,?y,?Z)是線性方程組(2.3)的解,則對于任意的α∈(0,),有(X(α),y(α),Z(α))∈NF(γ,Γ),其中

證先證明X(α)∈根據(jù)(2.3a)且X∈F0P,有〈Ai,X(α)〉=bi,i=1,···,m.由(3.13)及α <知α于是進而X(α)=因此X(α)∈F0P.

令

則易知N(α)非奇異,且N(α)E(α)N(α)?1=Q(α).根據(jù)文[2]的引理3.3 有

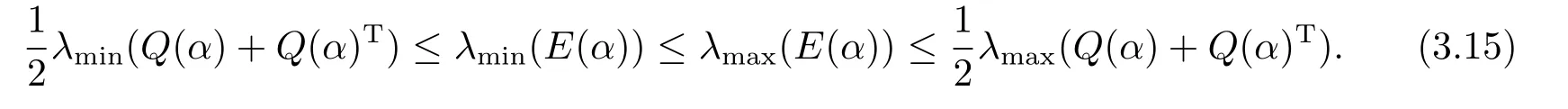
由(3.9)和(3.13)知≤,于是結(jié)合(3.8)和(3.15),得

將(3.14)的第二式代入上述左邊不等式,得

于是,有

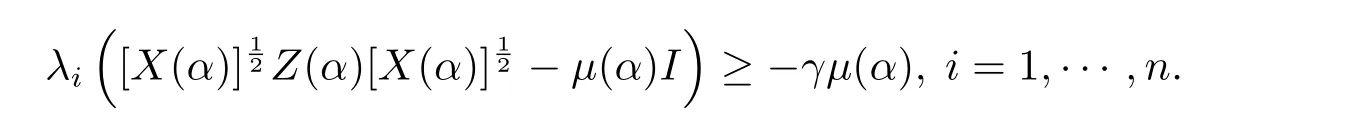
故

類似可得

于是

下面證明(X(α),y(α),Z(α))∈F0D.根據(jù)(3.16),設(shè)γ∈[0,1),得

由此可知X(α)Z(α)?0,結(jié)合X(α)?0 即知Z(α)?0.由(X,y,Z)∈F0D及(2.3b)知

因此,(X(α),y(α),Z(α))∈F0D.

綜合以上證明即知(X(α),y(α),Z(α))∈NF(γ,Γ).

引理3.4假設(shè)(A1)-(A3)成立,X∈F0P,(X,y,Z)∈F0D,(?X,?y,?Z) 是線性方程組(2.3) 的解,則

證證明中需用到以下兩個不等式(見文[11]):

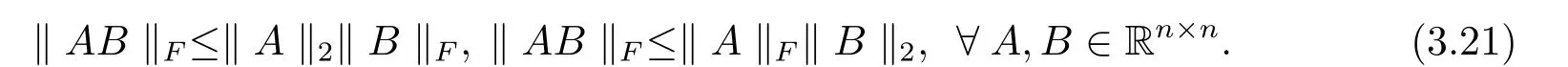
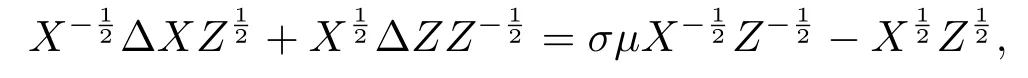
從而

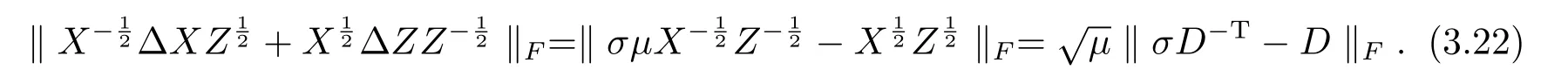
根據(jù)矩陣F-范數(shù)的定義和矩陣內(nèi)積的性質(zhì)有

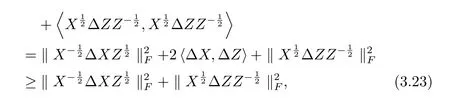
其中最后一個不等式是利用了引理2.1(1).于是由(3.22)和(3.23)即得

且

即(3.17)成立.

根據(jù)(3.21),(3.17)及矩陣D的定義,得

即(3.18)成立.

根據(jù)(3.21),(3.24)及矩陣D的定義,得

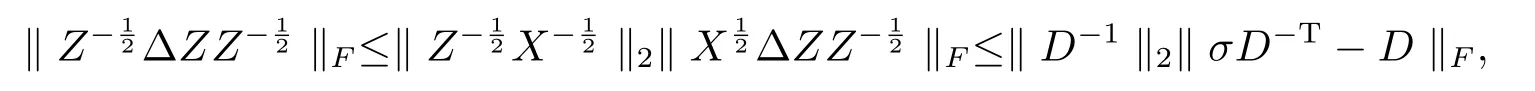
即(3.19)成立.

由(3.21),(3.19)及矩陣D的定義,得

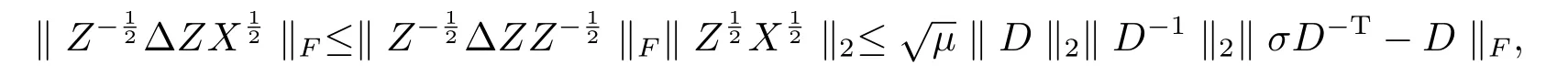
即(3.20)成立.

參照文[2]的引理5.7,可得如下結(jié)論:

引理3.5設(shè)矩陣W非奇異且則對于任意的有

下面定理給出了算法3.1 的一次迭代后迭代點(X(α),y(α),Z(α))的性質(zhì).

定理3.1假設(shè)(A1)-(A3)成立,(X,y,Z)∈NF(γ,Γ),Γ≥γ,(?X,?y,?Z)是線性方程組(2.3)的解.令

則對于任意的α∈[0,],有

證根據(jù)引理3.3,我們只需證明≤,即證

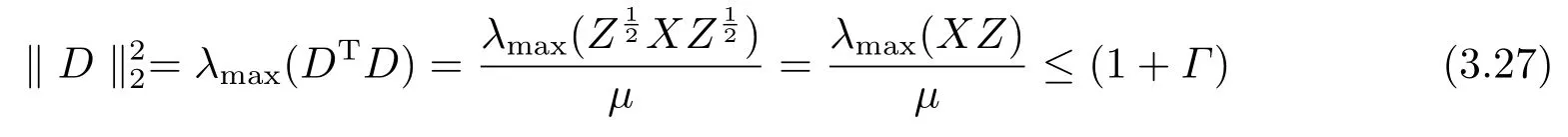
和

根據(jù)(3.28)和引理3.5,得

根據(jù)(3.17),(3.20),(3.27)-(3.29),有

將(3.25)代入上式,即得

根據(jù)(3.18),(3.28),(3.29)和(3.25),可得

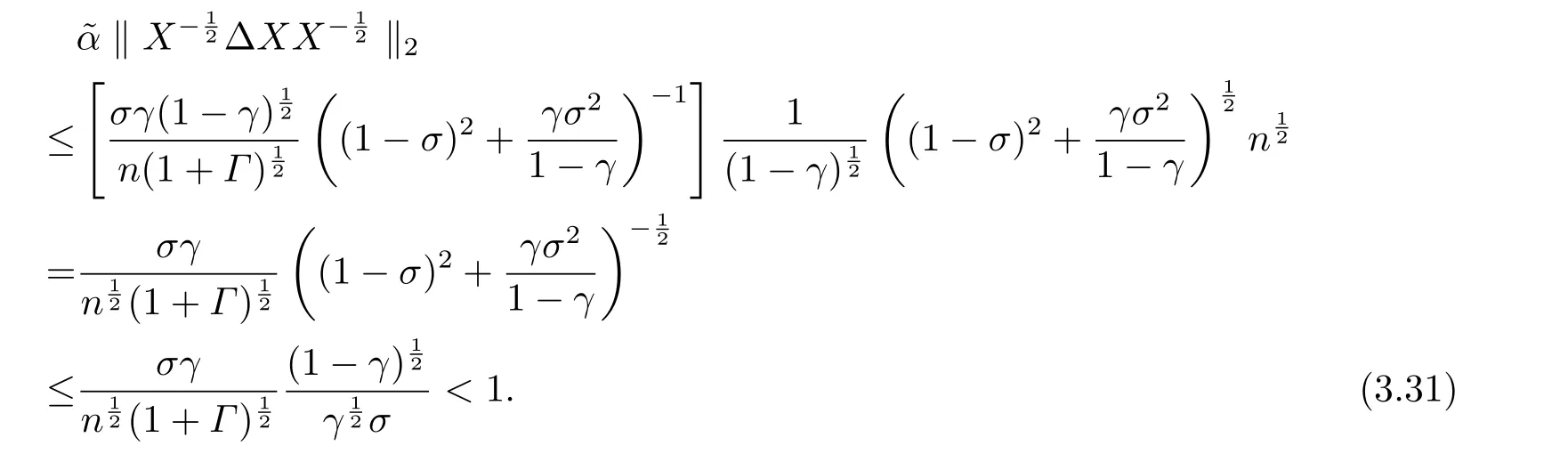
綜合(3.30)-(3.32)即知不等式(3.26)成立.

基于定理3.1,算法3.1 中步長αk的選取方法如下:對于任意的k≥0,取

下面分析證明算法3.1 的迭代復(fù)雜度,為此需作如下進一步假設(shè):

假設(shè)(A4)滿足不等式:

定理3.2假設(shè)(A1)-(A4)成立,對于任意的?>0,算法3.1 至多經(jīng)次迭代可得到一個?-最優(yōu)解,其中

證根據(jù)(2.4)及假設(shè)(A4),有

根據(jù)定理3.1和(3.33)得αk≥τ/(1?2σ),代入上式,即得

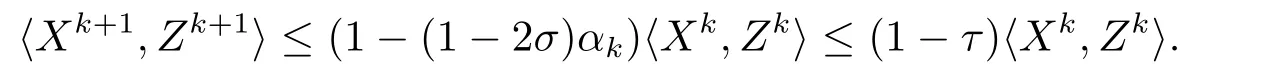
于是有

因此結(jié)論成立.