LIU Ying(劉英),KONG Hang(孔航)

( 1.College of Mathematics and Information Science,Hebei University,Baoding 071002,China;2.Key Laboratory of Machine Learning and Computational Intelligence,Hebei University,Baoding 071002,China)

Abstract: In this paper,we present a modification for the viscosity approximation method for fixed point problems of a nonexpansive mapping in Hilbert spaces.The modification removes a control condition of the viscosity approximation method.We establish a strong convergence theorem for the modified algorithm.

Key words: Nonexpansive mapping;Metric projection;Fixed point;Contraction;Viscosity approximation method

1.Introduction

LetCbe a nonempty closed convex subset of a real Hilbert spaceH.Recall that a self-mappingf:C→Cis anα-contraction if there exists a constantα∈[0,1) such that

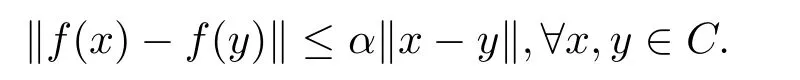
ΠCdenotes the set of all contractions onC.Note thatfhas a unique fixed point inC.

A mappingTofCinto itself is called nonexpansive if‖Tx?Ty‖≤‖x?y‖for allx,y∈C.Denote byF(T) the set of fixed points ofT,that is,F(T)={x∈C:Tx=x}.

Construction of fixed points of nonexpansive mappings is an important subject in the theory of nonexpansive mappings and its applications in a number of applied areas,in particular,in image recovery and signal processing (see,e.g.,[1-2]).

An important approximation method for nonexpansive mappings is to consider the sequence{xn} generated by the algorithm:

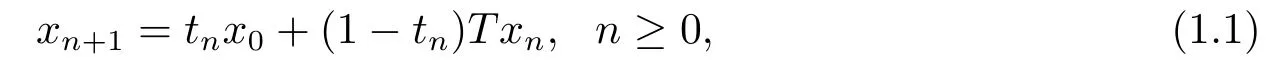
where the initial pointx0∈Cis taken arbitrarily and{tn}∞n=0is a sequence in the interval[0,1].We call the iteration process (1.1) the Halpern iteration algorithm because of the introduction by Halpern[3].

The algorithm(1.1)has been proved to be strongly convergent in both Hilbert spaces[3?4]and uniformly smooth Banach spaces[5?7]unless the sequence{tn} satisfies the following conditions:

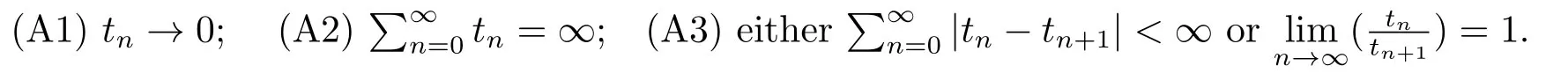
As mentioned in [8],the algorithm (1.1) has slow convergence due to the restriction of condition (A2).Moreover,it is shown in [3]that the conditions (A1) and (A2) are necessary,in the sense that if the algorithm (1.1) is always strongly convergent for all nonexpansive mappings fromCintoC,the conditions (A1) and (A2) must hold.So to improve the convergence rate of the algorithm (1.1),some additional steps have to be performed.For this purpose,Yanes and XU[8]proposed the following CQ method:

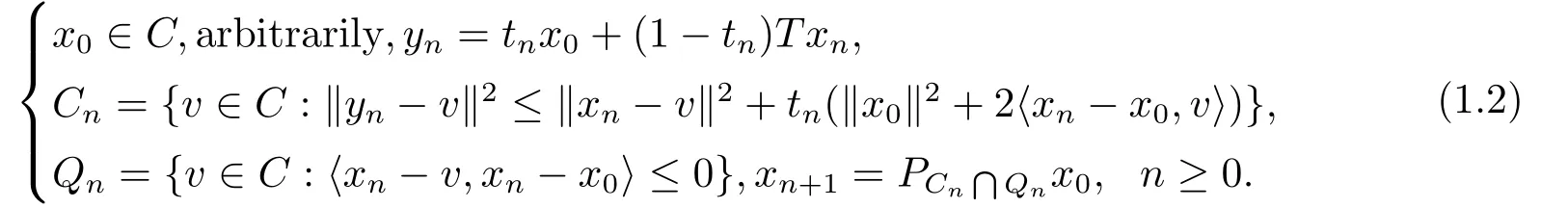
They proved the algorithm(1.2)has strong convergence under the condition(A1)only,which enhances the rate of convergence of the algorithm (1.1).More precisely,they proved the following theorem:

Theorem 1.1[8]LetHbe a real Hilbert space,andCbe a closed convex subset ofH.LetT:C→Cbe a nonexpansive mapping withF(T)≠?.Assume that{tn} ?(0,1)satisfying (A1).Then the sequence{xn} generated by (1.2) converges strongly toPF(T)x0.

In 2004,XU[9]studied the viscosity approximation algorithm for a nonexpansive mapping in a Hilbert space.More precisely,he proved the following theorem.

Theorem 1.2[9]LetHbe a real Hilbert space,andCbe a closed convex subset ofH.Assume thatT:C→Cis a nonexpansive mapping withF(T)≠?andf∈ΠC.Let{xn}be given by

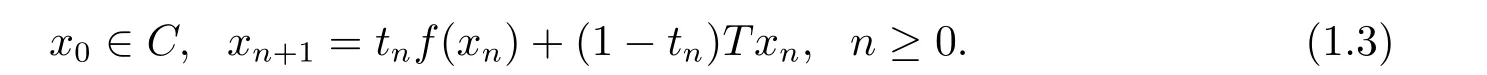
Then under the conditions (A1)-(A3),xn→x?,wherex?is the unique solution to the following variational inequality:

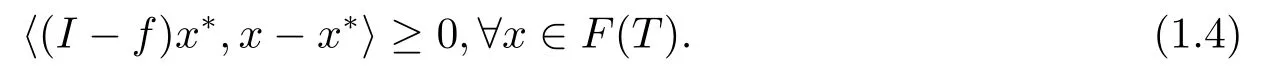
Clearly,It is an important property of the viscosity approximation algorithm to select a particular fixed point of a given nonexpansive mapping which is the unique solution to the variational inequality (1.4).

It is obvious that iff(x)≡x0for allx∈C,then the viscosity approximation method(1.4) reduces to the Halpern iteration method (1.1).We note that the conditions on the control sequence{tn}in(1.3)are the same as those in(1.1).Hence,according to the analysis about the Halpern iteration method (1.1) in [8],the viscosity approximation algorithm (1.3)has slow convergence due to the restriction of the condition (A2).

For this reason,we will modify the viscosity approximation algorithm and construct a new iterative algorithm by the idea of (1.2) to remove the the restriction of the condition(A2).

2.Preliminaries

LetHbe a real Hilbert space with inner productand the induced norm‖·‖,and letCbe a nonempty,closed and convex subset ofH.We writexn ?xto indicate that the sequence{xn}converges weakly toxandxn→xto indicate that the sequence{xn}converges strongly tox.We useωw(xn)={x:?xnj ?x} to denote the weakω-limit set of{xn}.

For each pointx∈H,there exists a unique nearest point denoted byPC(x) inC,that is,‖x?PC(x)‖≤‖x?y‖,?y∈C.

The mappingPC:H→Cis called the metric projection ofHontoC.It is well known thatPCis a nonexpansive mapping ofHontoC,i.e.,

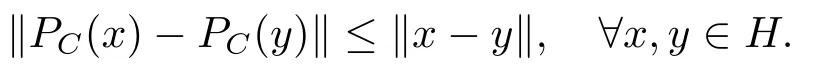
We recall some well known results which will be used in our analysis.

Lemma 2.1[10]For givenx∈Handy∈C:

(i)y=PC(x) if and only if

(ii)‖PC(x)?z‖2≤‖x?z‖2?‖x?PC(x)‖2,?z∈C.

Lemma 2.2[11]Let{xk} and{yk} be two bounded sequences inH,{βk} in [0,1].Suppose that

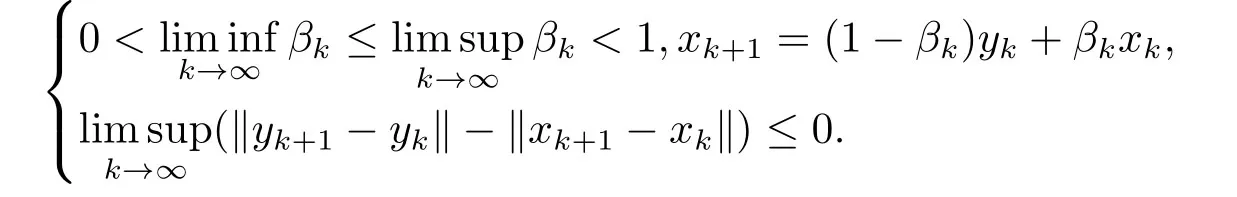
3.A Modification of the Viscosity Approximation Method

Inspired by the results of [10-11],we propose the following Algorithm 3.1 to remove the restriction of the condition (A2) for finding a fixed point of a nonexpansive mapping.

Algorithm 3.1Initialization.Chooseu∈C,x0∈C,positive sequences{tn},{βn},{γn}and{?n} such that

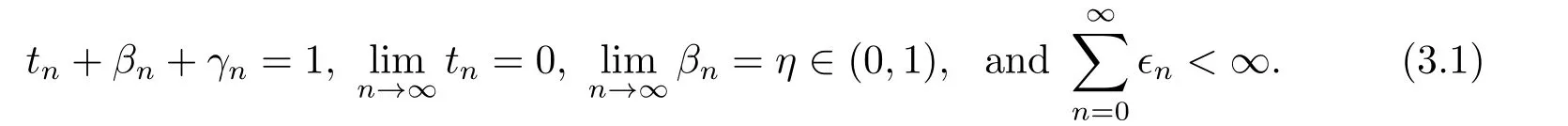
Step 1 Setxn,1:=f(xn).

Step 2 Inner loopj=1,2,...

Compute

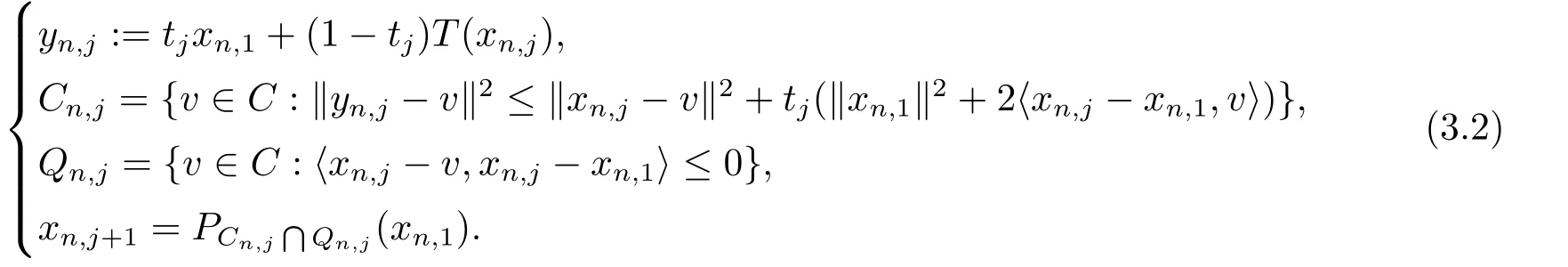
If‖xn,j+1?PF(T)(xn,1)‖≤?n,then sethn=xn,j+1and go to Step 3.Otherwise,increasejby 1 and repeat the inner loop Step 2.

Step 3 Setxn+1:=tnu+βnxn+γnhn.Then increasenby 1 and go to Step 1.

Remark 3.1By Theorem 1.1,we have{xn,j} generated by Step 2 of Algorithm 3.1 converges strongly to the pointPF(T)(f(xn))asj→∞.Consequently,we have that the inner loop in Algorithm 3.1 terminates after a finite number of steps.

Theorem 3.1LetHbe a real Hilbert space,andCbe a closed convex subset ofH.LetT:C→Cbe a nonexpansive mapping such thatF(T)≠?.Assume thatf:C→Cis anα-contraction.Then the sequence{xn} generated by Algorithm 3.1 converges strongly tox?∈F(T),wherex?is the unique solution to the variational inequality (1.4).

ProofBy Lemma 2.1,we have thatx?=PF(T)f(x?).SincePCis nonexpansive andfis contractive,we havex?is unique.Firstly,we observe that

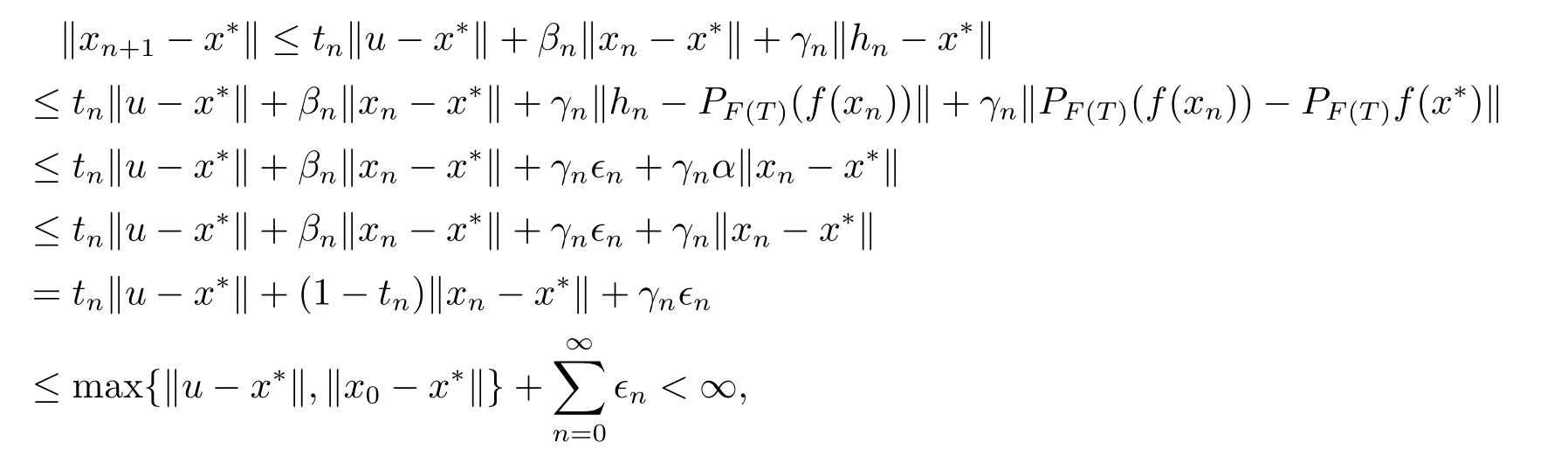
which implies that{xn} is bounded,and hence,{hn} is also bounded.Next,we prove thatWe denotexn+1=βnxn+(1?βn)ξn.Then,we have

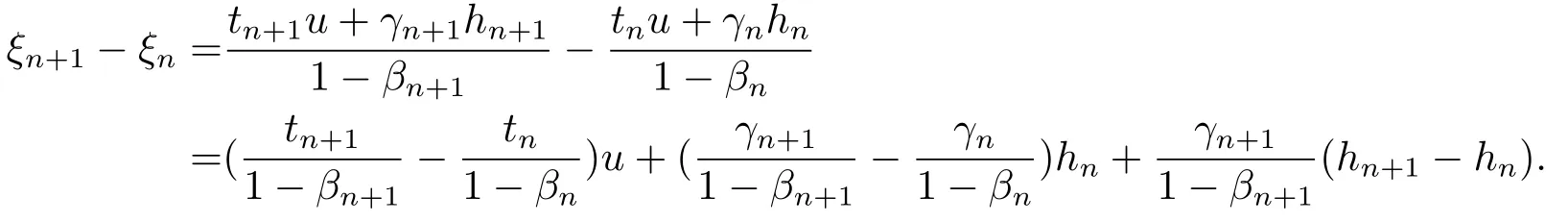
Thus,we get

From the assumptions in (3.1) and the boundness of {xn},it follows that

Now applying Lemma 2.2,we have

Byxn+1=βnxn+(1?βn)ξn,we obtain that

We observe that

Consequently,from (3.6),we have

which implies that

Since

we have that (1?α)‖xn?x?‖≤‖xn?PF(T)f(xn)‖→0,asn→∞.This shows thatxn→x?,asn→∞.

Remark 3.2Theorem 3.1 improves Theorem 3.2 in[9](i.e.Theorem 1.2 in this paper)in the following sense:

The condition (A2) is removed.Algorithm 3.1 converges strongly to the unique solution of the variational inequality (1.4) under only the condition (A1).